Với tóm tắt lý thuyết Toán lớp 6 Bài 19: Hình chữ nhật, hình thoi, hình bình hành, hình thang cân  sách Kết nối tri thức hay, chi tiết cùng với bài tập tự luyện chọn lọc giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán lớp 6.

Lý thuyết Toán lớp 6 Bài 19: Hình chữ nhật, hình thoi, hình bình hành, hình thang cân

Video giải Toán 6 Bài 19: hình chữ nhật. Hình thoi hình bình hành. Hình thang cân - Kết nối tri thức

A. Lý thuyết Hình chữ nhật, hình thoi, hình bình hành, hình thang cân

1. Hình chữ nhật

Trong hình chữ nhật có:

- Bốn góc bằng nhau và bằng 90⁰C.

- Các cặp cạnh đối bằng nhau.

- Hai đường chéo bằng nhau.

Ví dụ 1. Lấy ví dụ về các hình có dạng hình chữ nhật trong thực tiễn.

Lời giải

Mặt bàn, Mặt bảng, cửa ra vào, cửa sổ, …

2. Hình thoi

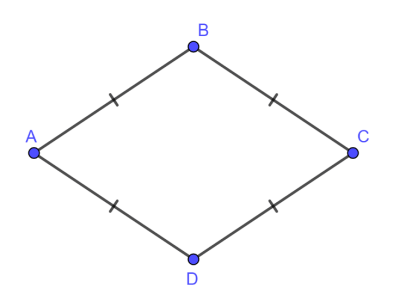
Trong hình thoi :

- Bốn cạnh bằng nhau.

- Hai đường chéo vuông góc với nhau.

- Các cặp góc đối bằng nhau.

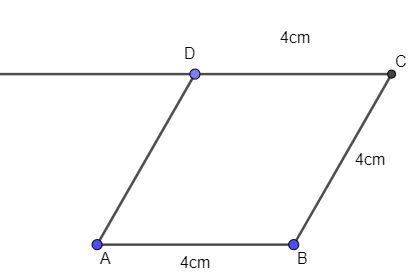
Ví dụ 2. Vẽ hình thoi cạnh 4cm.

Lời giải

Bước 1. Vẽ đoạn thẳng AB = 4cm.

Bước 2. Vẽ đoạn thẳng BC = 4cm (điểm C khác điểm A).

Bước 3. Qua điểm C vẽ đường thẳng song song với AB. Trên đường thẳng này lấy điểm D sao cho CD = 4cm.

Bước 4. Nối D với A ta được hình thoi ABCD.

3. Hình bình hành

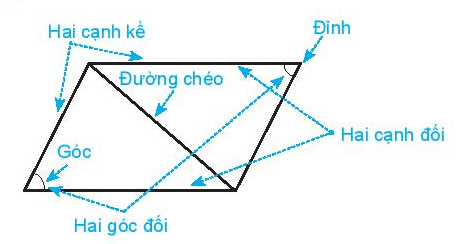
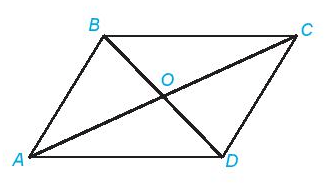
Trong hình bình hành:

- Các cặp cạnh đối bằng nhau.

- Hai đường chéo cắt nhau tại trung điểm của mỗi đường.

- Các cặp cạnh đối song song.

- Các cặp góc đối bằng nhau.

Ví dụ 3. Cho hình bình hành ABCD, hai đường chéo AC và BD cắt nhau tại điểm I. Sử dụng compa hoặc thước thẳng kiểm tra xem điểm I có là trung điểm của hai đường chéo không?

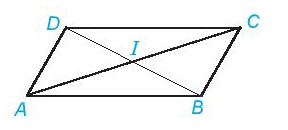
Lời giải

+) Nếu sử dụng compa:

- Đầu tiên mở một khoảng compa trùng với đoạn IA. Sau đó giữ nguyên khoảng đó đặt vào đoạn IC thấy trùng nhau.

- Tương tự mở compa một khoảng trùng với IB. Sau đó giữ nguyên khoảng đó đặt vào đoạn ID thấy trùng nhau.

Vậy điểm I chính là trung điểm của hai đường chéo.

+) Nếu sử dụng thước thẳng:

Ta sẽ đo độ dài của từng đoạn một, thì thấy IA = IC, IB = IB.

Vậy I chính là trung điểm của hai đường chéo.

4. Hình thang cân

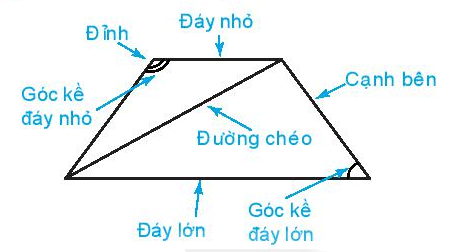
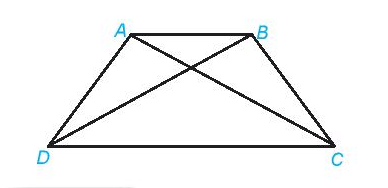
Trong hình thang cân:

- Hai cạnh bên bằng nhau.

- Hai đường chéo bằng nhau.

- Hai cạnh đáy song song với nhau.

- Hai góc kề một đáy bằng nhau.

Ví dụ 4. Hình nào trong các hình đã cho là hình thang cân? Hãy cho biết tên hình thang cân đó.

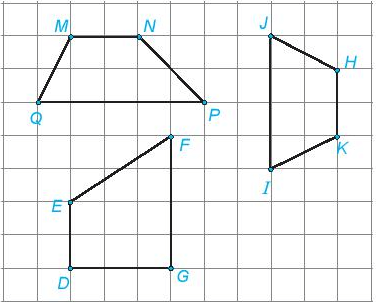
Lời giải

Đầu tiên lấy eke kiểm tra hai cạnh đáy có song song với nhau không.

Tiếp theo lấy thước thẳng đo độ dài hai đường chéo nếu bằng nhau thì là hình thang cân.

Từ kết quả đo, ta thấy các hình trên hình thang cân là HKIJ.

B. Bài tập

Bài 1. Hãy kể tên các hình thang cân, hình chữ nhật, hình thoi có trong lục giác đều sau: 

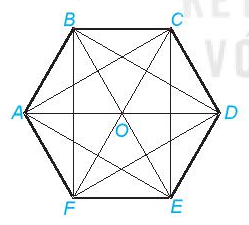
Lời giải

Trong hình đã cho:

- Hình thang cân: ABCD, BCDE, DEFA, EFAB.

- Hình chữ nhật: ACDF, BCEF.

- Hình thoi: ABOF, ABCO, BCDO, DEFO, CDEO, EFAO.

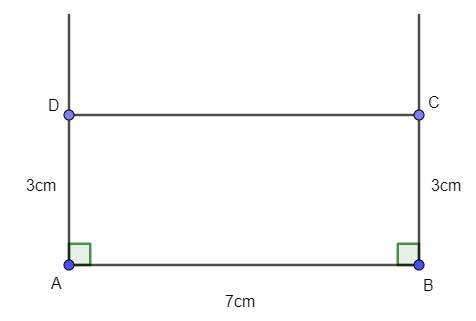
Bài 2. Vẽ hình chữ nhật có một cạnh dài 7cm, một cạnh 3cm.

Lời giải

Bước 1. Vẽ đoạn thẳng AB = 7cm.

Bước 2. Dựng đường thẳng vuông góc với AB tại A. Trên đường thẳng này lấy điểm D sao cho AD = 3cm.

Bước 3. Dựng đường thẳng vuông góc với AB tại B. Trên đường thẳng này lấy điểm C sao cho BC = 3cm.

Bước 4. Nối C với D ta được hình chữ nhật có AB = 7cm, AD = 3cm.

Bài giảng Toán 6 Bài 19: hình chữ nhật. Hình thoi hình bình hành. Hình thang cân - Kết nối tri thức

Xem thêm các bài tóm tắt lý thuyết Toán 6 Kết nối tri thức hay, chi tiết khác:

Lý thuyết Bài 18: Hình tam giác đều, hình vuông, hình lục giác đều

Lý thuyết Bài 19: Hình chữ nhật, hình thoi, hình bình hành, hình thang cân

Lý thuyết Bài 20: Chu vi và diện tích của một số tứ giác đã học

Lý thuyết Bài 21: Hình có trục đối xứng

Lý thuyết Bài 22: Hình có tâm đối xứng