Với tóm tắt lý thuyết Toán lớp 6 Bài 22: Hình có tâm đối xứng sách Kết nối tri thức hay, chi tiết cùng với bài tập tự luyện chọn lọc giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán lớp 6.

Lý thuyết Toán lớp 6 Bài 22: Hình có tâm đối xứng

Video giải Toán 6 Bài 22: Hình có tâm đối xứng - Kết nối tri thức

A. Lý thuyết Hình có tâm đối xứng

1. Hình có tâm đối xứng trong thực tế

Mỗi hình có mổ điểm O, mà khi quay hình đó xung quanh điểm O đúng một nửa vòng thì hình thu được “trùng khít” với chính nó ở vị trí ban đầu (trước khi quay).

Những hình như thế được gọi là “hình có tâm đối xứng” và điểm O được gọi là “tâm đối xứng” của hình.

Ví dụ 1. Đoạn thẳng là một hình có tâm đối xứng. Tâm đối xứng của nó là điểm nào?

Lời giải

Cho đoạn thẳng AB có trung điểm là điểm O

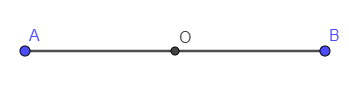
Khi quay đoạn thẳng AB xung quanh điểm O đúng nửa vòng ta thư được hình sau:

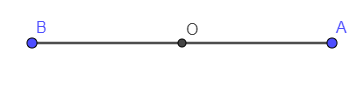
Hình thu được là một hình trùng khít với hình ban đầu. 

Do đó đoạn thẳng là một hình có tâm đối xứng và tâm đối xứng của nó là điểm O.

Ví dụ 2. Trong những hình nào dưới đây hình nào có tâm đối xứng? Hãy dự đoán tâm đối xứng và kiểm tra bằng cách quay nửa vòng.

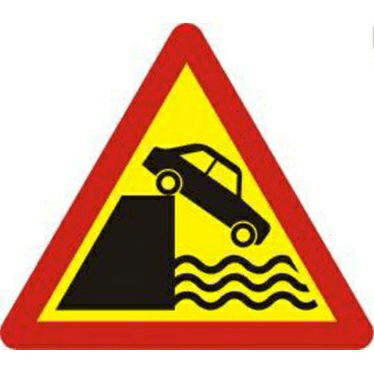
             Hình a                                 Hình b                                    Hình c

Lời giải

Hình có tâm đối xứng là hình a

Tâm đối xứng của hình là tâm O của đường tròn.

Khi quay biển báo một nửa vòng quanh tâm O ta được:

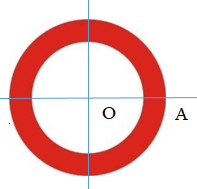
Hình này trùng khít với hình ban đầu.

Do đó hình này có tâm đối xứng và tâm đối xứng là tâm O của đường tròn.

2. Tâm đối xứng của một số hình phẳng

Tâm đối xứng của hình bình hành, hình thoi, hình vuông, hình chữ nhật là giao điểm của hai đường chéo.

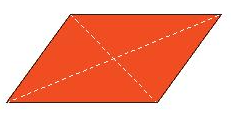
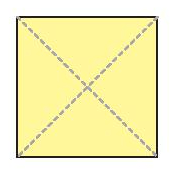
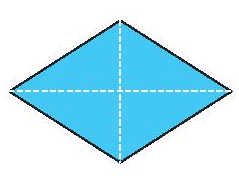
Tâm đối xứng của hình lục giác đều là giao điểm của các đường chéo chính.

B. Bài tập

Bài 1. Trong những hình dưới đây, hình nào có tâm đối xứng?

Lời giải

Các hình có tâm đối xứng là: Hình a, Hình c và Hình d.

Các hình này khi quay quanh tâm đối xứng một nửa vòng đều trùng khít với hình ban đầu.

Bài 2. Trong các hình sau đây hình nào vừa có tâm đối xứng, hình nào vừa có trục đối xứng: Hình chữ nhật, hình thang, hình bình hành, hình thoi, hình vuông, hình tròn, hình lục giác đều.

Lời giải

- Hình chữ nhật có hai trục đối xứng là đường nối hai trung điểm của hai cạnh đối diện và tâm đối xứng là giao của hai đường chéo.

- Hình thang không có trục đối xứng, cũng ko có tâm đối xứng.

- Hình hình hành không có trục đối xứng và có tâm đối xứng là giao điểm của hai đường chéo.

- Hình thoi là hình có hai trục đối xứng là hai đường chéo và tâm đối xứng là giao điểm của hai đường chéo.

- Hình vuông có 4 trục đối xứng và tâm đối xứng là giao điểm của hai đường chéo.

- Hình tròn là hình có vô số trục đối xứng và có tâm đối xứng là tâm đường tròn.

- Hình lục giác đều có trục đối xứng và có tâm đối xứng là giao điểm của ba đường chéo chính.

Vậy các hình vừa có tâm đối xứng, hình nào vừa có trục đối xứng: Hình chữ nhật, hình thoi, hình vuông, hình tròn, hình lục giác đều.

Bài giảng Toán 6 Bài 22: Hình có tâm đối xứng - Kết nối tri thức

Xem thêm các bài tóm tắt lý thuyết Toán 6 Kết nối tri thức hay, chi tiết khác:

Lý thuyết Bài 21: Hình có trục đối xứng

Lý thuyết Bài 22: Hình có tâm đối xứng

Lý thuyết Bài 23: Mở rộng phân số. Phân số bằng nhau

Lý thuyết Bài 24: So sánh phân số. Hỗn số dương

Lý thuyết Bài 25: Phép cộng và phép trừ phân số