Tailieumoi.vn xin giới thiệu Trắc nghiệm Toán lớp 10 Chương 8: Đại số tổ hợp sách Kết nối tri thức. Bài viết gồm 30 câu hỏi trắc nghiệm với đầy đủ các mức độ và có hướng dẫn giải chi tiết sẽ giúp học sinh ôn luyện kiến thức và rèn luyện kĩ năng làm bài trắc nghiệm Toán 10.
Trắc nghiệm Toán 10 Chương 8: Đại số tổ hợp
I. Nhận biết
Câu 1. Một hoán vị của tập hợp gồm n phần tử là:
A. một cách sắp xếp có thứ tự n phần tử đó (với n là một số tự nhiên và n ≥ 1);
B. một cách sắp xếp có thứ tự n – 1 phần tử (với n là một số tự nhiên và n ≥ 1);
C. một cách sắp xếp có thứ tự k (k < n) phần tử (với n là một số tự nhiên và n ≥ 1);
D. một cách sắp xếp có thứ tự n + 1 phần tử (với n là một số tự nhiên và n ≥ 1).
Đáp án: A
Giải thích:
Một hoán vị của tập hợp gồm n phần tử là một cách sắp xếp có thứ tự n phần tử đó (với n là một số tự nhiên và n ≥ 1).
Câu 2. Giả sử một công việc có thể thực hiện theo một trong hai phương án khác nhau:
- Phương án 1 có n1 cách thực hiện;
- Phương án 2 có n2 cách thực hiện (không trùng với bất kì phương án thực hiện nào của cách số 1)
Vậy số cách thực hiện công việc có:
A. n1 + n2 (cách thực hiện);
B. n1 . n2 (cách thực hiện);
C. (cách thực hiện);
D. n2 – n1 (cách thực hiện).
Đáp án: A
Giải thích:
Áp dụng quy tắc cộng, số cách thực hiện công việc: n1 + n2 (cách thực hiện).
Vậy ta chọn A.
Câu 3. Trong đội văn nghệ của nhà trường có 8 học sinh nam và 6 học sinh nữ. Hỏi có bao nhiêu cách chọn một đôi song ca nam nữ:
A. 91;
B. 182;
C. 48;
D. 14.
Đáp án: C
Giải thích:
Để chọn một đôi song ca nam nữ diễn văn nghệ có thể xem là một công việc gồm hai công đoạn:
+ Công đoạn 1: Chọn 1 học sinh nam có 8 cách chọn
+ Công đoạn 2: Chọn 1 học sinh nữ có 6 cách chọn
Áp dụng quy tắc nhân: có 6.8 = 48 cách chọn học sinh để tạo thành một đôi song ca nam nữ.
Câu 4. Một tổ gồm 3 học sinh nữ và 7 học sinh nam. Số cách để sắp xếp số học sinh trong tổ thành một hàng dọc là:
A. 3! + 7!;
B. 10!;
C. 3!.7!;
D. 21.
Đáp án: B
Giải thích:
Mỗi cách sắp xếp 10 học sinh trong tổ thành một hàng dọc là một hoán vị của 10 học sinh đó
Vậy có số cách để sắp xếp số học sinh trong tổ thành hàng dọc là 10!
Câu 5. Điền từ vào chỗ trống để được một phát biểu đúng:
Giả sử một công việc phải được hoàn thành qua hai ... liên tiếp nhau:
- ... 1 có m1 cách thực hiện;
- Với mỗi cách thực hiện ... 1, có m2 cách thực hiện ... 2 .
Khi đó số cách thực hiện công việc là: m1.m2 cách.
A. giai đoạn;
B. công đoạn;
C. công đoạn và giai đoạn;
D. giai đoạn và công đoạn.
Đáp án: B
Giải thích:
Một công việc phải được hoàn thành qua hai công đoạn liên tiếp nhau:
- Công đoạn 1 có m1 cách thực hiện;
- Với mỗi cách thực hiện công đoạn 1, có m2 cách thực hiện công đoạn 2 .
Khi đó số cách thực hiện công việc là: m1.m2 cách.
Câu 6. Ta có khai triển đa thức: (x – 1)4 = x4 − 4x3 + 6x2 − 4x + 1. Hệ số của hạng tử có chứa x3 là:
A. 4;
B. – 4;
C. 6;
D. – 6
Đáp án: C
Giải thích:
Ta có: (x – 1)4 = x4 − 4x3 + 6x2 − 4x + 1.
Số hạng chứa x3 là – 4x3
Do đó hệ số của hạng tử chứa x3 là – 4.
Câu 7. Có 3 cây bút đỏ và 4 cây bút xanh trong một hộp bút. Hỏi có bao nhiêu cách lấy ra một cây bút từ hộp bút?
A. 4;
B. 12;
C. 7;
D. 3.
Đáp án: C
Giải thích:
Để chọn một cây bút từ hộp bút ta có 2 phương án:
+ Phương án 1: Lấy 1 cây bút đỏ từ 3 cây bút đỏ: có 3 cách
+ Phương án 2: Lấy một cây bút xanh từ 4 cây bút xanh có 4 cách
Vậy có 3 + 4 = 7 cách lấy một cây bút từ một hộp bút.
Câu 8. Một khu di tích lịch sử có 4 cửa Đông; Tây; Nam; Bắc. Một người đi vào tham quan rồi đi ra, khi vào và ra phải đi hai cửa khác nhau. Tất cả các cách đi vào và đi ra của người đó là:
A. 8;
B. 12;
C. 16;
D. 4.
Đáp án: B
Giải thích:
Việc lựa chọn cổng đi vào đi ra của khách tham quan có thể xem như là một công việc gồm 2 công đoạn:
+ Công đoạn 1: Chọn cổng đi vào có: 4 cách chọn
+ Công đoạn 2: Chọn cổng đi ra có : 3 cách chọn
Áp dụng quy tắc nhân, có 4.3 = 12 cách chọn cổng để đi vào và đi ra sau khi tham quan của du khách.
Câu 9. Để giải một bài tập cần phải giải hai bài tập. Bài tập 1 có 9 cách giải, bài tập 2 có 5 cách giải . Số các cách để hoàn thành bài tập trên là :
A. 3;
B. 45;
C. 5;
D. 12.
Đáp án: B
Giải thích:
Việc hoàn thành bài tập có thể xem như một công việc gồm 2 công đoạn:
+ Công đoạn 1: giải bài tập 1: 9 cách
+ Công đoạn 2: Giải bài tập 2: 5 cách
Áp dụng quy tắc nhân có 9.5 = 45 cách giải đề hoàn thành bài tập.
Câu 10. Cho sơ đồ cây sau:
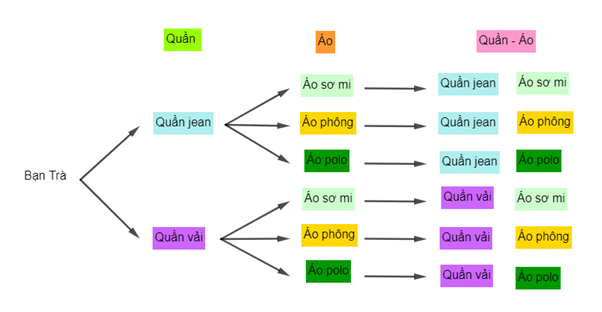
Dựa vào sơ đồ cây bạn Trà có bao nhiêu cách chọn bộ quần và áo để đi học?
A. 2;
B. 3;
C. 5;
D. 6.
Đáp án: D
Giải thích:
Dựa vào sơ đồ cây ta có: Trà có 6 cách chọn quần và áo để đi học bao gồm:
Quần jean và áo sơ mi, quần jean và áo phông, quần jean và áo polo; quần vải và áo sơ mi, quần vải và áo phông, quần vải và áo polo.
Vậy ta chọn A.
II. Thông hiểu
Câu 1. Trong cuộc thi tìm hiểu lịch sử Việt Nam, ban tổ chức công bố các đề tài bao gồm :8 đề tài lịch sử, 7 đề tài thiên nhiên, 10 đề tài về con người và 6 đề tài về văn hoá. Mỗi thí sinh được quyền chọn 1 đề tài. Hỏi mỗi thí sinh có bao nhiêu khả năng lựa chọn đề tài
A. 20 ;
B. 3360;
C. 31;
D. 30.
Đáp án: C
Giải thích:
Việc lựa chọn chủ đề tham gia cuộc thi tìm hiểu của mỗi thí sinh có 4 phương án:
+ Phương án 1: Chọn đề tài lịch sử có 8 cách chọn
+ Phương án 2: Chọn đề tài thiên nhiên có 7 cách chọn
+ Phương án 3: Chọn đề tài con người có 10 cách chọn
+ Phương án 4: Chọn đề tì văn hoá có 6 cách chọn
Vậy để chọn một đề tài trong cuộc thi mỗi thí sinh có: 8 +7 +10 + 6 = 31
Câu 2. Giả sử bạn muốn mua một áo sơ mi cỡ 39 hoặc 40 . Áo cỡ 39 có 5 màu khác nhau, áo cỡ 40 có 4 màu khác nhau. Hỏi có bao nhiêu sự lựa chọn về màu áo và cỡ áo
A. 9;
B. 5;
C. 4;
D. 1.
Đáp án: A
Giải thích:
Việc thực hiện lựa chọn áo có thể thực hiện theo hai phương án:
Phương án 1: Cho áo cỡ 39: 5 lựa chọn
Phương án 2: Chọn áo cỡ 40 có 4 lựa chọn
Áp dụng quy tắc cộng có 5 + 4 = 9 cách lựa chọn áo.
Câu 3. Cho lục giác ABCDEF. Có bao nhiêu vectơ khác , có điểm đầu và điểm cuối là hai đỉnh của lục giác.
A. 62;
B. 26;
C. ;
D. .
Đáp án: D
Giải thích:
Mỗi cách chọn 2 đỉnh trong 6 đỉnh để sắp xếp thành một vectơ là một chỉnh hợp chập 2 của 6
Vậy có vectơ khác , có điểm đầu và điểm cuối là hai đỉnh của lục giác ABCDEF.
Câu 4. Từ sáu chữ số 1; 2; 3; 4; 5; 6 có thể lập được bao nhiêu số tự nhiên bé hơn 100?
A. 36;
B. 62;
C. 54;
D. 42.
Đáp án: D
Giải thích:
Từ 6 chữ số đã cho để lập được các số tự nhiên bé hơn 100, ta có hai phương án:
+ Phương án 1: số tự nhiên có 1 chữ số: có 6 số
+ Phương án 2: Số tự nhiên có 2 chữ số:
Gọi số tự nhiên có hai chữ số có dạng (a ≠ 0)
a có 6 cách chọn
b có 6 cách chọn
Do đó, áp dụng quy tắc nhân có 6.6 = 36 chữ số có 2 chữ số được tạo thành từ 6 số đã cho
Vậy có 36 + 6 = 42 số tự nhiên được tạo thành từ 6 số đã cho và nhỏ hơn 100.
Câu 5. Có hai chuồng gà, chuồng thứ nhất nhốt 3 gà trống và 4 gà mái, chuồng 2 nhốt 4 gà trống và 5 gà mái. Hỏi có bao nhiêu cách bắt 1 lần 2 con gà trong đó có 1 gà trống và 1 gà mái từ một trong hai chuồng đã cho?
A. 12;
B. 32;
C. 20;
D. 240.
Đáp án: B
Giải thích:
Phương án 1: Chuồng được chọn là chuồng 1
Bắt 1 con gà trống có 3 cách
Bắt 1 con gà mái có 4 cách
Do đó có 4. 3 = 12 cách bắt 1 con gà trống và 1 con gà mái từ chuồng 1.
Phương án 2: Chuồng được chọn là chuồng 2
Bắt 1 con gà trống có 4 cách
Bắt 1 con gà mái có 5 cách
Do đó có 4. 5 = 20 cách bắt 1 con gà trống và 1 con gà mái từ chuồng 2
Vậy có 12 + 20 = 32 cách để bắt gà thoả mãn yêu cầu bài toán
Câu 6. Trong một kì thi THPT Quốc gia tại một điểm thi có 5 sinh viên tình nguyện được phân công trực hướng dẫn thí sinh thi ở 5 vị trí khác nhau. Yêu cầu mỗi vị trí có đúng 1 sinh viên. Hỏi có nhiêu cách phân công vị trí trực cho 5 người đó.
A. 120;
B. 625;
C. 3125;
D. 80.
Đáp án: A
Giải thích:
Sắp xếp 5 sinh viên vào 5 vị trí là một hoán vị của 5
Vậy có 5! = 120 cách phân công vị trí cho 5 sinh viên.
Câu 7. Từ các số 0; 1; 2; 3; 4; 5 có thể lập bao nhiêu số tự nhiên có 3 chữ số khác nhau và không chia hết cho 5
A. 80;
B. 20;
C. 64;
D. 192.
Đáp án: C
Giải thích:
Gọi số tự nhiên có ba chữ số có dạng (a ≠ 0)
Vì số tự nhiên cần tìm không chia hết cho 5 nên c ∈ {1; 2; 3; 4}
⇒ c có 4 cách chọn;
a khác 0 và c nên a có 4 cách chọn;
b khác c và a nên b có 4 cách chọn.
Vậy áp dụng quy tắc có 4.4.4 = 64 số tự nhiên thoả mãn yêu cầu bài toán.
Câu 8. Trên giá sách có 10 quyển sách Toán khác nhau, 8 quyển sách Tiếng Anh khác nhau và 6 quyển sách Lí khác nhau. Hỏi có bao nhiêu cách chọn hai quyển sách không cùng thuộc một môn?
A. 80;
B. 480 ;
C. 188;
D. 60.
Đáp án: C
Giải thích:
Số cách chọn 1 quyển sách toán là 10 cách
Số cách chọn 1 quyển sách tiếng anh là 8 cách
Số cách chọn 1 quyển sách lí là 6 cách
+ Phương án 1: 1 sách toán và 1 sách tiếng anh có 10. 8 = 80 cách
+ Phương án 2: 1 sách toán và 1 sách lí có 10. 6 = 60 cách
+ Phương án 3: 1 sách lí và 1 sách tiếng anh có 6.8 = 48 cách
Vậy có 80 + 60 + 48 = 188 cách chọn hai quyển sách không cùng thuộc một môn
Câu 9. Sắp xếp năm bạn học sinh An; Bình; Chi; Lệ ; Dũng vào một chiếc ghế dài có 5 chỗ ngồi. Số cách sắp xếp sao cho Chi luôn ngồi chính giữa là:
A. 24;
B. 120;
C. 60;
D. 16.
Đáp án: A
Giải thích:
Để bạn Chi ngồi ở giữa chỉ có 1 sự lựa chọn
Số cách xếp 4 bạn sinh An, Bình, Dũng, Lệ vào 4 chỗ còn lại là một hoán vị của 4 phần tử nên có có 4! = 24 cách.
Vậy có 1.24 = 24 cách xếp.
Câu 10. Lớp 10A có 38 học sinh. Giáo viên muốn chọn 3 bạn học sinh cho 3 vị trí ban cán sự. Hỏi giáo viên có bao nhiêu cách lựa chọn?
A. 114;
B. 50616;
C. 8436;
D. 38!.
Đáp án: C
Giải thích:
Mỗi cách chọn 3 học sinh trong 38 học sinh là một tổ hợp chập 3 của 38
Vậy có = 8436 cách chọn 3 học sinh cho vị trí ban cán sự.
Câu 11. Cho tập hợp E gồm 10 phần tử. Hỏi có bao nhiêu tập con có 8 phần tử của tập hợp E?
A. 100;
B. 80;
C. 45;
D. 90.
Đáp án: C
Giải thích:
Mỗi tập hợp con 8 phần tử của tập hợp được tạo thành là một tổ hợp chập 8 của 10
Vậy số tập hợp con có 8 phần tử của E là:
Câu 12. Cho tập hợp S = {1; 2; 3; 4; 5; 6}. Có thể lập được bao nhiêu số tự nhiên gồm 4 chữ số khác nhau lấy từ tập hợp S?
A. 360;
B. 120;
C. 15;
D. 20.
Đáp án: A
Giải thích:
Mối cách chọn ra 4 chữ số khác nhau từ tập S và sắp xếp để tạo thành số có 4 chữ số là một chỉnh hợp chập 4 của 6
Vậy có = 360 số tự nhiên có 4 chữ số được tạo thành từ 4 chữ số khác nhau của tập hợp S
Câu 13. Từ 5 bông hồng vàng, 3 bông hồng trắng, 4 bông hồng đỏ (các bông hồng xem như khác nhau). Người ta muốn chọn ra một bó gồm 7 bông . Có bao nhiêu cách chọn 1 bó hoa trong đó có ít nhất 3 bông hồng vàng và ít nhất 3 bông hồng đỏ:
A. 120;
B. 130;
C. 140;
D. 150.
Đáp án: D
Giải thích:
Để chọn 1 bó hoa trong đó có ít nhất 3 bông hồng vàng và ít nhất 3 bông hồng đỏ có 3 phương án thực hiện như sau:
+ Phương án 1: Chọn 3 bông hồng vàng, 3 bông hồng đỏ và 1 bông hồng trắng có: = 120 cách
+ Phương án 2: Chọn 4 bông hồng vàng, 3 bông hồng đỏ có: = 20 cách
+ Phương án 3: Chọn 3 bông hồng vàng, 4 bông hồng đỏ có: = 10 cách
Vậy có: 120 + 20 + 10 = 150 cách chọn 1 bó hoa trong đó có ít nhất 3 bông hồng vàng và ít nhất 3 bông hồng đỏ.
Câu 14. Hệ số của hạng tử không chứa x là k trong khai triển của . Nhận xét nào sau đây đúng về k:
A. k ∈ (14; 24);
B. k ∈ (28; 38);
C. k ∈ (32; 42);
D. k ∈ (44; 54).
Đáp án: B
Giải thích:
=
= .
Do đó hạng tử không chứa x là 24.
Vì vậy k = 24 ∈ (28; 38).
Câu 15. Giá trị của biểu thức bằng:
A. 252;
B. 352;
C. 452;
D. 425.
Đáp án: B
Giải thích:
= −
=
= 10. 25 + 20. 5 + 2 = 352.
III. Vận dụng
Câu 1. Tính tổng S =
A. 10005;
B. 9995;
C. 9985;
D. 10015.
Đáp án: A
Giải thích:
Xét khai triển:
(999 + x)5 =
Thay x = 1 vào hai vế của khai triển ta có:
(999 + 1)5 =
Vậy tổng S = (999 + 1)5 = 10005.
Câu 2. Cho hình vuông ABCD. Trên cạnh AB; CD; DA lần lượt lấy 1; 2; 3 và n điểm phân biệt n ≥ 3 khác A; B; C; D. Tìm n biết số tam giác lấy từ n + 6 điểm trên là 439:
A. n =12;
B. n = 20;
C. n = 10;
D. n = 8.
Đáp án: C
Giải thích:
Chọn 3 điểm bất kì trong n + 6 điểm đã cho có cách
Trên cạnh CD chọn ra được 1 bộ ba điểm thẳng hàng.
Trên cạnh DA chọn được bộ ba điểm thẳng hàng.
Vì mỗi tam giác được tạo thành từ 3 điểm không thẳng hàng.
Nên số tam giác được tạo thành là – – 1 = 439
⇔ – = 440
⇔ – = 440
⇔ – = 440
⇔ – = 440
⇔ (n + 6)(n + 5)(n + 4) – n(n – 1)(n – 2) = 2640
⇔ n3 + 15n2 + 74n + 120 – (n3 – 3n2 + 2n) = 2640
⇔18n2 + 72n + 120 = 2640
⇔ n2 + 4n – 140 = 0
⇔
Vậy n = 10.
Câu 3. Kết thúc buổi liên hoan khi ra về, mọi người đều bắt tay nhau. Số người tham dự là bao nhiêu biết số cái bắt tay là 28:
A. 14;
B. 7;
C. 8;
D. 28.
Đáp án: C
Giải thích:
Gọi n là số người tham gia buổi liên hoan (n ∈ ℕ*)
Mỗi người bắt tay n – 1 người còn lại nên có n(n – 1) cái bắt tay
Tuy nhiên mỗi cái như vậy được tính 2 lần nên thực tế có cái bắt tay
Do đó ta được phương trình = 28 hay n2 – n – 56 = 0 .
Vậy chỉ có 8 người tham gia buổi tiệc.
Câu 4. Có bao nhiêu số chẵn gồm 3 chữ số phân biệt nhỏ hơn 547:
A. 80;
B. 128;
C. 114;
D. 149.
Đáp án: D
Giải thích:
Gọi số có 3 chữ số phân biệt là được lập từ dãy số 0; 1; 2; 3; 4; 5; 6; 7; 8; 9
- Phương án 1: a ∈ {1; 3}⇒ a có 2 cách chọn
c ∈ {0; 2; 4; 6; 8}⇒ c có 5 cách chọn
b có 8 cách chọn
Do đó có 2. 5. 8 = 80 số
- Phương án 2: a ∈ {2; 4}⇒ a có 2 cách chọn
c ∈ {0; 6; 8}⇒ c có 3 cách chọn
b có 8 cách chọn
Do đó có 2. 3. 8 = 48 số
- Phương án 3: a = 5
+ Trường hợp 1: b = 4 thì c ∈ {0; 2; 6}, c có 3 cách chọn;
+ Trường hợp 2: b < 4 thì b ∈ {0; 1; 2; 3}.
Nếu b ∈ {0; 2} có 2 cạnh chọn và c có 4 cách chọn. Do đó có: 2.4 = 8 số.
Nếu b ∈ {1; 3} có 2 cách chọn và c có 5 cách chọn. Do đó có: 2.5 =10 số.
Như vậy có 10 + 8 + 3 = 21 số.
Vậy có 80 + 48 + 21 = 149
Câu 5. Giả sử hệ số của x trong khai triển của bằng 640. Xác định giá trị của r
A. r = 1;
B. r = 2;
C. r = 3;
D. r = 4.
Đáp án: D
Giải thích:
Ta có:
= .
Theo giả thiết ta có: 10r3 = 640 ⇒ r3 = 64 ⇒ r = 4.
Xem thêm các bài trắc nghiệm Toán 10 Kết nối tri thức hay, chi tiết khác:
Trắc nghiệm Bài 24: Hoán vị, tổ hợp, chỉnh hợp
Trắc nghiệm Bài 25: Nhị thức Newton
Trắc nghiệm Bài ôn tập cuối chương 8
Trắc nghiệm Bài 26: Biến cố và định nghĩa cổ điển của xác suất
Trắc nghiệm Bài 27: Thực hành tính xác suất theo định nghĩa cổ điển