Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu Chủ đề 6 - Hình chữ nhật , tài liệu bao gồm 4 trang. Tài liệu được tổng hợp từ các tài liệu ôn thi hay nhất  giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kỳ thi sắp hới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây

Tóm tắt tài liệu

Chuyên đề hình học: hình chữ nhật. Lý thuyết và bài tập vận dụng, có giải chi tiết.

Chủ đề 6: Hình chữ nhật

A. Mục tiêu

- Ôn tập cho học sinh các tính chất của hình chữ nhật.
- Dấu hiệu nhận biết hình chữ nhật
- Rèn luyện khả năng vẽ hình, chứng minh một bài toán.
B. Thời lượng: 3 tiết (tiết 15, 16, 17)

C. Thực hiện

Tiết 15:

Bài 1: Tìm x trên hình bên (Đv đo: cm)
Giải:

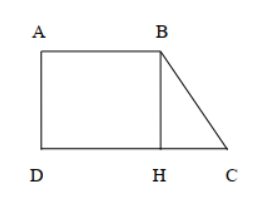
Khi BH ^ CD. Tứ giác ABHD có 3 góc vuông nên là hình chữ nhật, do đó:

DH = AB = 16cm

\( \Rightarrow HC = DC - DH = 24 - 16 = 8cm\)

Xét \(\Delta BHC\)vuông theo định lí Pitago

\(BH = \sqrt {B{C^2} - H{C^2}}  = \sqrt {{{17}^2} - {8^2}}  = \sqrt {225}  = 15cm\)

Vậy x = 15cm
Bài 2: Tứ giác ABCD có hai đường chéo vuông góc với nhau. Gọi E, F, G, H theo
thứ tự là trung điểm của các cạnh AB, BC, CD, DA. Tứ giác EFGH là hình gì? Vì
sao?
Giải:

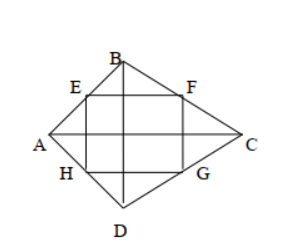
Tam giác ABC có AE = EB, BF = FC

\( \Rightarrow EF = AC(1)\)

Chứng minh tương tự: EH// HG (*)

Chứng minh tương tự: EH// FG(**)

Từ (*) và (**) \( \Rightarrow \)EFGH là hình bình hành.

EF//AC, \(BD \bot AC \Rightarrow EF \bot BD\)

\(EF \bot BD,EH//BD \Rightarrow EF \bot EH\)

Hình bình hành EFGH có góc E= 90⁰

\( \Rightarrow \)là hình chữ nhật

Bài 3: Cho tam giác ABC vuông cân tại A, AC = 4cm, Điểm M thuộc cạnh BC.
Gọi D, E theo thứ tự là chân các đường vuông góc kẻ từ M đến AB, AC.
a. Tứ giác EDME là hình gì? tính chu vi tứ giác đó.
b. Điểm M ở vị trí nào trên cạnh BC thì đoạn thẳng DE có độ dài nhỏ nhất.
Giải:

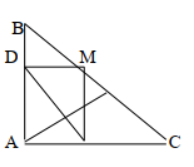
a. Tứ giác ADME có góc <A=<D=<E=90⁰

Vậy tứ giác ADME là hình chữ nhật.

- Chu vi của hình chữ nhật ADME bằng:

2(AD+DM)=2(AD+DB)=2AB

=2.4=8cm

b. Gọi H là trung điểm của BC, ta có \(AH \bot BC\)

ADME là hình chữ nhật \( \Rightarrow \)DE=AM

Ta có: DE= AM>AH

Dấu “=” xảy ra khi \(M \equiv H\)

Vậy DE có độ dài nhỏ nhất là AH khi M là trung điểm của BC
Tiết 16:
Bài 4: Cho tam giác ABC cân tại A, các đường trung tuyến BM, CN cắt nhau tại
G. Gọi D là điểm đối xứng với G qua M. Gọi E là điểm đối xứng với G qua N. Tứ

giác BEDC là hình gì? Vì sao?

Giải:

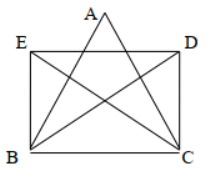
D đối xứng với G qua M \( \Rightarrow \)GD= 2GM

G là trọng tâm tam giác ABC

\( \Rightarrow BG = 2GM \Rightarrow BG = GD\)

Chứng minh tương tự: CG=GE

Tứ giác BEDC có hai đường chéo cắt nhau tại trung điểm của mỗi đường nên là hình bình hành \(\Delta CBM = \Delta BCN(c.g.c) \Rightarrow  < {B_1} =  < {C_1}\)

\( \Rightarrow BG = CG \Rightarrow BD = CE\)

Hình bình hành BEDC có hai đường chéo bằng nhau nên là hình chữ nhật

Bài 5: Cho tam giác ABC vuông tại A . Điểm D thuộc cạnh AC. Gọi E, F, G theo
thứ tự là trung điểm của BD , BC, DC. Chứng minh rằng tứ giác EFEG là hình thang cân

Giải

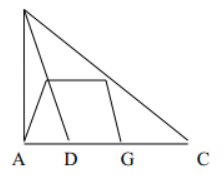
Vì EF là đường trung bình của tam giác BDC nên EF // DC
Do đó: AEFG là hình thang
Do FG là đường trung bình của tam giác BDC

Nên FG // BD Þ góc <G1 = <D1 (đồng vị)
Vì tam giác ABD vuông tại A, AE là đường trung tuyến nên \(AE = \frac{{BD}}{2} = ED\)

Do đó: tam giác AED cân tại E \( \Rightarrow \)góc <A1 = <D1

Từ đó góc <G1 = <A1
Hình thang AEFG có hai góc kÌ một đáy bằng nhau nên là hình thang cân.
Tiết 17:
Bài 6: Cho tam giác ABC vuông tại A, đường cao AH, đường trung tuyến AM
a. CMR: Góc <HAB = <MAC
b. Gọi D, E thứ tự là chân đường vuông góc kẻ từ H đến AB, AC. CMR AM

vuông góc với DE

Giải

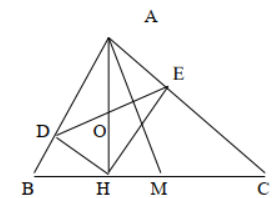
a. Ta có góc <A1 = <C (cùng phụ với <HAC)

AM là trung tuyến ứng với cạnh huyền của tam giác ABC Þ AM = MC

Þ góc <C = <A2 Þ góc <A1 = <A2

b. Gọi O là giao điểm của AH và DE

I là giao điểm của AM và DE
Tứ giác ADHE là hình chữ nhật (có 3 góc vuông)
Þ OA = OE Þ góc <E1 = <OAE (1)

Ta lại có: \(\Delta AHC\)vuông

\( \Rightarrow \)góc <C+<OAE=90⁰(2)

Ta có: góc <C=<A₂(3)(cm ở câu a)

Từ (1), (2), (3) \( \Rightarrow \)góc <E₁+<A₂=90⁰

\( \Rightarrow \)Góc <AIE=90⁰ tức \(AM \bot DE\)

Bài 7: Cho tam giác ABC vuông tại A, đường cao AH. Gọi D, E theo thứ tự là chân đường vuông góc kẻ từ H đến AB, AC.
a. CMR: AH = DE
b. Gọi I là trung điểm của HB, K là trung điểm của HC
CMR: DI // EK
Giải:

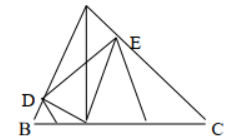
a. Tứ giác ADHE có 3 góc vuông nên là hình chữ nhật

Do đó: AH= DE

b. Gọi O là giao điểm của AH và DE
ADHE là hình chữ nhật

\( \Rightarrow OH = OE \Rightarrow \)góc <E₁=<H₁(1)

Tam giác EHC vuông có EK là đường trung tuyến ứng với cạnh huyền

\( \Rightarrow \)HK=EK \( \Rightarrow \)góc <E₂=<H₂(2)

\( \Rightarrow \)Từ (1), (2) \( \Rightarrow \)góc <E₁+<E₂=<H₁+<H₂=<AHC=90⁰

Do đó: góc DEK =90⁰

Chứng minh tương tự ta có: góc EDI=90⁰                                               

Vậy DI// EK(đpcm)