Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu Các chuyên đề học sinh giỏi hình học môn Toán lớp 8, tài liệu bao gồm 150 trang. Tài liệu được tổng hợp từ các tài liệu ôn thi hay nhất  giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kỳ thi sắp hới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây

Tóm tắt tài liệu

Các chuyên đề bài tập hình học dành cho học sinh giỏi lớp 8, đi kèm lời giải chi tiết.

Chuyên đề 1 – Các bài toán về đinh lí Ta – let

A. Kiến thức

1. Định lí Ta – lét:

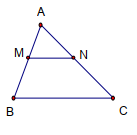
* Định lí Ta – lét: \(\left. \begin{array}{l}\Delta ABC\\MN//BC\end{array} \right\} \Leftrightarrow \frac{{AM}}{{AB}} = \frac{{AN}}{{AC}}\)

* Hệ quả: MN// BC \( \Rightarrow \frac{{AM}}{{AB}} = \frac{{AN}}{{AC}} = \frac{{MN}}{{BC}}\)

B. Bài tập áp dụng:

Bài 1:

Cho tứ giác ABCD, đường thẳng A song song với BC cắt BD ở E, đường thẳng qua B song song với AD cắt AC ở G

a) chứng minh EG//CD

b) Giả sử AB//CD, chứng minh AB² = CD. EG

Giải

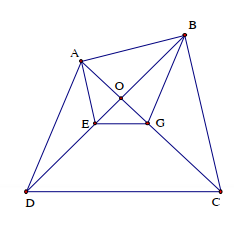
Gọi O là giao điểm của AC và BD

a) Vì AE// BC \( \Rightarrow \frac{{OE}}{{OB}} = \frac{{OA}}{{OC}}(1)\)

BG//AC \( \Rightarrow \frac{{OB}}{{OD}} = \frac{{OG}}{{OA}}(2)\)

Nhân (1) với (2) vế theo vế ta có: \(\frac{{OE}}{{OD}} = \frac{{OG}}{{OC}} \Rightarrow EG//CD\)

b) Khi AB//CD thì EG// AB//CD, BG//AD nên

\(\frac{{AB}}{{EG}} = \frac{{OA}}{{OG}} = \frac{{OD}}{{OB}} = \frac{{CD}}{{AB}} \Rightarrow \frac{{AB}}{{EG}} = \frac{{CD}}{{AB}} \Rightarrow A{B^2} = CD.EG\)

Bài 2:

Cho ABC vuông tại A, Vẽ ra phía ngoài tam giác đó các tam giác ABD vuông cân ở B, ACF vuông cân ở C. Gọi H là giao điểm của AB và CD, K là giao điểm của AC và BF. Chứng minh rằng:

a) AH= AK

b) AH² = BH.CK

Giải

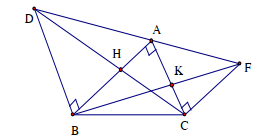
Đặt AB=c, AC=b

BD//AC(cùng vuông góc với AB)

Nên \(\frac{{AH}}{{HB}} = \frac{{AC}}{{BD}} = \frac{b}{c} \Rightarrow \frac{{AH}}{{HB + AH}} = \frac{b}{{b + c}}\)

Hay \(\frac{{AH}}{{AB}} = \frac{b}{{b + c}} \Rightarrow \frac{{AH}}{c} = \frac{b}{{b + c}} \Rightarrow AH = \frac{{b.c}}{{b + c}}\)(1)

AB//CF ( cùng vuông góc với AC ) nên

\(\frac{{AK}}{{KC}} = \frac{{AB}}{{CF}} = \frac{c}{b} \Rightarrow \frac{{AK}}{{KC + AK}} = \frac{c}{{b + c}}\)

Hay \(\frac{{AK}}{{AC}} = \frac{b}{{b + c}} \Rightarrow \frac{{AK}}{b} = \frac{c}{{b + c}} \Rightarrow AK = \frac{{b.c}}{{b + c}}(2)\)

Từ (1) và (2) suy ra: AH= AK

b) Từ \(\frac{{AH}}{{HB}} = \frac{{AC}}{{BD}} = \frac{b}{c}\) và \(\)\(\frac{{AK}}{{KC}} = \frac{{AB}}{{CF}} = \frac{c}{b}\)

suy ra \(\frac{{AH}}{{HB}} = \frac{{KC}}{{AK}} \Rightarrow \frac{{AH}}{{HB}} = \frac{{KC}}{{AH}}\)( Vì AH= AK)

\( \Rightarrow \)AH² = BH. KC

3. Bài 3: Cho hình bình hành ABCD, đường thẳng a đi qua A lần lượt cẳ BD, BC, DC theo thứ tự tại E, K, G. Chứng minh rằng:

a) AE² = EK. EG

b) \(\frac{1}{{AE}} = \frac{1}{{AK}} + \frac{1}{{AG}}\)

c) Khi đường thẳng a thay đổi vị trí nhưng vẫn qua A thì tích BK, DG có giá trị không đổi

Giải

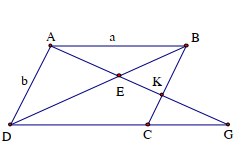
a) Vì ABCD là hình bình hành và \(K \in BC\)NÊN AD//BK, theo hệ quả của định lí Ta – lét ta có:

\(\frac{{EK}}{{AE}} = \frac{{EB}}{{ED}} = \frac{{AE}}{{EG}} \Rightarrow \frac{{EK}}{{AE}} = \frac{{AE}}{{EG}} \Rightarrow A{E^2} = EK.EG\)

b) Ta có: \(\frac{{AE}}{{AK}} = \frac{{DE}}{{DB}};\frac{{AE}}{{AG}} = \frac{{BE}}{{BD}}\)nên

\(\begin{array}{l}\frac{{AE}}{{AK}} + \frac{{AE}}{{AG}} = \frac{{BE}}{{BD}} + \frac{{DE}}{{DB}} = \frac{{BD}}{{BD}} = 1\\ \Rightarrow AE(\frac{1}{{AK}} + \frac{1}{{AG}}) = 1\\ \Rightarrow \frac{1}{{AE}} = \frac{1}{{AK}} + \frac{1}{{AG}}\end{array}\)(đpcm)

c) Ta có:

\(\begin{array}{l}\frac{{BK}}{{KC}} = \frac{{AB}}{{CG}} \Rightarrow \frac{{BK}}{{KC}} = \frac{a}{{CG}}(1);\\\frac{{KC}}{{AD}} = \frac{{CG}}{{DG}} \Rightarrow \frac{{KC}}{b} = \frac{{CG}}{{DG}}(2)\end{array}\)

Nhân (1) với (2) vế theo vế ta có: \(\frac{{BK}}{b} = \frac{a}{{DG}} \Rightarrow BK.DG = ab\) không đổi ( vì a= AB, b=AD là độ dài hai cạnh của hình bình hành ABCD không đổi)

4. Bài 4

Cho tứ giác ABCD, các điểm E, F, G, H theo thứ tự chia trong các cạnh AB, BC, CD, DA theo tỉ số 1:2. Chứng minh rằng:

a) EG=FH

b) EG vuông góc với FH

Giải

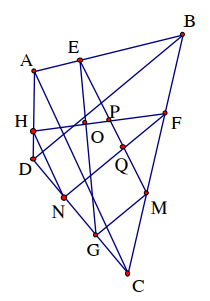
Gọi M, N theo thứ tự là trung điểm của CF, DG

Ta có \(CM = \frac{1}{2}CF = \frac{1}{3}BC \Rightarrow \frac{{BM}}{{BC}} = \frac{1}{3} \Rightarrow \frac{{BE}}{{BA}} = \frac{{BM}}{{BC}} = \frac{1}{3}\)

\( \Rightarrow EM//AC \Rightarrow \frac{{EM}}{{AC}} = \frac{{BM}}{{BE}} = \frac{2}{3} \Rightarrow EM = \frac{2}{3}AC(1)\)

Tương tự ta cso: NF//BC \( \Rightarrow \frac{{NF}}{{BD}} = \frac{{CF}}{{CB}} = \frac{2}{3} \Rightarrow NF = \frac{2}{3}BD(2)\)

Mà AC=BD (3)

Từ (1), (2), (3) suy ra: EM=NF (a)

Tương tự như trên ta có: MG//BD, NH//AC và \(MG = NH = \frac{1}{3}AC(b)\)

Mặt khác EM//AC; MG//BD và \(AC \bot BD \Rightarrow \widehat {EMG} = {90^0}\)(4)

Tương tự, ta có \(\widehat {FNH} = {90^0}(5)\)

Từ (4) và (5) suy ra \(\widehat {EMG} = \widehat {FNH} = {90^0}\)(c)

Từ (a), (b), (c) suy ra \[\Delta EMG = \Delta FNH\](c.g.c) \( \Rightarrow EG = FH\)

b) Gọi giao điểm của EG và FH là O; của EM và FH là P; của EM và FN là Q thì

\[\widehat {PQF} = {90^0} \Rightarrow \widehat {QPF} + \widehat {QFP} = {90^0}\]mà \[\widehat {QPF} = \widehat {OPE}\]( đối đỉnh), \[\widehat {OEP} = \widehat {OFP}(\Delta EMG = \Delta FNH)\]

Suy ra \(\widehat {EOP} = \widehat {PQF} = {90^0} \Rightarrow EO \bot OP \Rightarrow EG \bot FH\)

5. Bài 5:

Cho hình thang ABCD có đáy nhỏ CD. Từ D vẽ đường thẳng song song với BC, cắt AC tại M và Ab tại K . Từ C vẽ đường thẳng song song với AD, cắt AB tại F, qua F ta lại vẽ đường thẳng song song với AC, cắt BC tại P. Chứng minh rằng

a) MP//AB

b) Ba đường thẳng MP, CF, DB đồng quy

Giải

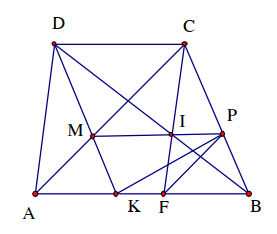
AK//CD \( \Rightarrow \frac{{CM}}{{AM}} = \frac{{DC}}{{AK}}\)(2)

Các tứ giác AFCD, DCBK là các hình bình hành nên AF=DC, FB=AK (3)

Kết hợp (1), (2) và (3) ta có \(\frac{{CP}}{{PB}} = \frac{{CM}}{{AM}} \Rightarrow \)MP//AB ( định lí ta – lét đảo) (4)

b) Gọi I là giao điểm của BD và CF, ta có: \(\frac{{CP}}{{PB}} = \frac{{CM}}{{AM}} = \frac{{DC}}{{AK}} = \frac{{DC}}{{FB}}\)

Mà \(\frac{{DC}}{{FB}} = \frac{{DI}}{{IB}}\)( DO FB//DC) \( \Rightarrow \frac{{CP}}{{PB}} = \frac{{DI}}{{IB}} \Rightarrow IP//DC//AB\)(5)

Từ (4) và (5) suy ra: qua P có hai đường thẳng IP, PM cùng song song với AB//DC nên theo tiên đề Ơ clits thì ba điểm P, I, M thẳng hàng hay MP đi qua giao điểm của CF và DB hay ba đường thẳng MP, CF, DB đồng quy

6. Bài 6

Cho \(\Delta ABC\)có BC< BA. Qua C kẻ đường thẳng vuông góc với tia phân giác BE của \(\widehat {ABC}\); đường thẳng này cắt BE tại F và cắt trung tuyến BD tại G. Chứng minh rằng đoạn thẳng EG bị đoạn thẳng DF chia thành hai phần bằng nhau

Giải

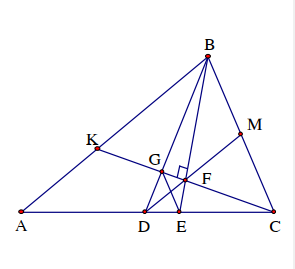
Gọi K là giao điểm của CF và AB; M là giao điểm của DF và BC

\(\Delta KBC\) có BF vừa là phân giác vừa là đường cao nên \(\Delta KBC\)cân tại B

\( \Rightarrow \)BK=BC và FC=FK

Mặt khác D là trung điểm AC nên DF là đường trung bình của \(\Delta AKC\)

\( \Rightarrow \)DF//AK hay DM//AB

Suy ra M là trung điểm BC

\(DF = \frac{1}{2}AK\)( DF là đường trung bình của \(\Delta AKC\)), ta có

\(\frac{{BG}}{{GD}} = \frac{{BK}}{{DF}}\)( do DF// BK) \( \Rightarrow \frac{{BG}}{{GD}} = \frac{{BK}}{{DF}} = \frac{{2BK}}{{AK}}(1)\)

Mốt khác \(\frac{{CE}}{{DE}} = \frac{{DC - DE}}{{DE}} = \frac{{DC}}{{DE}} - 1 = \frac{{AD}}{{DE}} - 1\)( Vì AD= DC)\( \Rightarrow \frac{{CE}}{{DE}} = \frac{{AE - DE}}{{DE}} = \frac{{DC}}{{DE}} - 1 = \frac{{AD}}{{DE}} - 1\)

Hay \(\frac{{CE}}{{DE}} = \frac{{AE - DE}}{{DE}} - 1 = \frac{{AE}}{{DE}} - 2 = \frac{{AB}}{{DF}} - 2\)

( vì \(\frac{{AE}}{{DE}} = \frac{{AB}}{{DF}}:\)Do DF//AB)

Suy ra \(\frac{{CE}}{{DE}} = \frac{{AK + BK}}{{DE}} - 2 = \frac{{2(AK + BK)}}{{AK}} - 2\)

( Do\(DF = \frac{1}{2}AK) \Rightarrow \frac{{CE}}{{DE}}\)\( = \frac{{2(AK + BK)}}{{AK}} - 2 = \frac{{2BK}}{{AK}}(2)\)

Từ (1) và (2) suy ra \(\frac{{BG}}{{GD}} = \frac{{CE}}{{DE}} \Rightarrow EG//BC\)

Gọi giao điểm của EG và DF là O ta có

\(\frac{{OG}}{{MC}} = \frac{{OE}}{{MB}}( = \frac{{FO}}{{FM}}) \Rightarrow OG = OE\)

Bài tập về nhà

Bài 1:

Cho tứ giác ABCD, AC và BD cắt nhau tại O. Đường thẳng qua O và song song với BC cắt AB ở E; đường thẳng song song với CD qua O cắt AD tại F

a) Chứng minh FE//BD

b) Từ O kẻ các đường thẳng song song với AB, AD cắt BD, CD tại G và H.

Chứng minh: CG.DH=BG.CH

Bài 2:

Cho hình bình hành ABCD, điểm M thuộc cạnh BC, điểm N thuộc tia đối của tia BC sao cho BN=CM; các đường thẳng DN, DM cắt AB theo thứ tự E, F.

Chứng minh:

a) AE²= EB. FE

b) \(EB = {(\frac{{AN}}{{DF}})^2}.EF\)