Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu Chuyên đề hàm số bậc nhất và bậc hai, tài liệu bao gồm 52 trang. Tài liệu được tổng hợp từ các tài liệu ôn thi hay nhất  giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kỳ thi sắp hới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây

Chuyên đề hàm số bậc nhất và bậc hai

Chủ đề 2: Hàm số bậc nhất và bậc hai

Bài 1: Hàm số

I - Ôn tập về hàm số

1. Hàm số. Tập xác định của hàm số

Giả sử có hai đại lượng biến thiên x và y, trong đó x nhận giá trị thuộc tập số D.

- Nếu với mỗi giá trị của x thuộc tập D có một và chỉ một giá trị tương úng của x thuộc tập số thực \(\mathbb{R}\) thì ta có một hàm số.

- Ta gọi x là biến số và y là hàm số của x

- Tập hợp D được gọi là tập xác định của hàm số.

2. Cách cho hàm số

Một hàm số có thể được cho bằng các cách sau.

- Hàm số cho bằng bảng

- Hàm số cho bằng biểu đồ

- Hàm số cho bằng công thức

Tập xác định của hàm số \(y = f(x)\) là tập hợp tất cả các số thực x sao cho biểu thức f(x) có nghĩa.

3. Đồ thị của hàm số

Đồ thị của hàm số \(y = f(x)\) xác định trên tập D là tập hợp tất cả các điểm M(x; f(x)) trên mặt phẳng tọa độ với x thuộc D.

II – Sự biến thiên của hàm số

1. Ôn tập

- Hàm số \(y = f(x)\) gọi là đồng biến (tăng) trên khoảng (a;b) nếu

\(\forall {x_1},{x_2} \in (a;b):{x_1} < {x_2} \Rightarrow f\left( {{x_1}} \right) < f\left( {{x_2}} \right).\)

- Hàm số y= f(x) gọi là nghịch biến ( giảm) trên khoảng (a;b) nếu

\(\forall {x_1},{x_2} \in (a;b):{x_1} < {x_2} \Rightarrow f\left( {{x_1}} \right) > f\left( {{x_2}} \right){\rm{. }}\)

2. Bảng biến thiên

Xét chiều biến thiên của một hàm số là tìm các khoảng đồng biến và các khoảng nghịch biến của nó. Kết quả xét chiều biến thiên được tổng kết trong một bảng gọi là bảng biến thiên.

Ví dụ. Dưới đây là bảng biến thiên của hàm số \(y = {x^2}\).

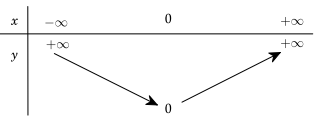
Hàm số \(y = {x^2}\) xác định trên khoảng (hoặc trong khoảng) \(( - \infty ; + \infty )\) và khi x dần tới \( + \infty \) hoặc dần tới \( - \infty \) thì y đều dần tới \( + \infty \).

Tại \(x = 0\) thì \(y = 0\).

Để diễn tả hàm số nghịch biến trên khoảng \(( - \infty ;0)\) ta vẽ mũi tên đi xuống (từ \( + \infty \) đến 0).

Để diễn tả hàm số đồng biến trên khoảng \((0; + \infty )\) ta vẽ mũi tên đi lên (từ 0 đến \( + \infty \) )

Nhìn vào bảng biến thiên, ta sơ bộ hình dung được đồ thị hàm số (đi lên trong khoảng nào, đi xuống trong khoảng nào).

III - Tính chã̃n lẻ của hàm số

1. Hàm số chẵn, hàm số lẻ

- Hàm số \(y = f(x)\) với tập xác định D gọi là hàm số chẵn nếu

\(\forall x \in {\rm{D th\`i  }} - x \in {\rm{D v\`a  }}f( - x) = f(x){\rm{. }}\)

- Hàm số \(y = f(x)\) với tập xác định D gọi là hàm số lẻ nếu

\(\forall x \in {\rm{D th\`i  }} - x \in {\rm{D v\`a  }}f( - x) =  - f(x){\rm{. }}\)

2. Đồ thị của hàm số chẵn, hàm số lẻ

- Đồ thị của hàm sỗ chẵn nhận trục tung làm trục đối xứng

- Đồ thị của hàm sỗ lẻ nhận gốc tọa độ làm tâm đối xứng

Câu hỏi trắc nghiệm

Vấn đề 1. Tính giá trị của hàm số

Câu 1. Điểm nào sau đây thuộc đồ thị hàm số \[y = \frac{1}{{x - 1}}\]

A. \({M_1}(2;1)\).

B. \({M_2}(1;1)\).

C. \({M_3}(2;0)\).

D. \({M_4}(0; - 1)\).

Lời giải. Xét đáp án \({\rm{A}}\), thay \(x = 2\) và \(y = 1\) vào hàm số \(y = \frac{1}{{x - 1}}\) ta được \(1 = \frac{1}{{2 - 1}}\) : thỏa mãn. Chọn A.

Câu 2. Điểm nào sau đây thuộc đồ thị hàm số \(y = \frac{{\sqrt {{x^2} - 4x + 4} }}{x}\).

A. \(A(1; - 1)\).

B. \(B(2;0)\).

C. \(C\left( {3;\frac{1}{3}} \right)\).

D. \(D( - 1; - 3)\).

Lời giải. Xét đáp án \(A\), thay \(x = 1\) và \(y =  - 1\) vào hàm số \(y = \frac{{\sqrt {{x^2} - 4x + 4} }}{x}\) ta được \( - 1 = \frac{{\sqrt {{1^2} - 4.1 + 4} }}{1} \Leftrightarrow  - 1 = 1\) : không thỏa mãn.

Xét đáp án \(B\), thay \(x = 2\) và \(y = 0\) vào hàm số \(y = \frac{{\sqrt {{x^2} - 4x + 4} }}{x}\) ta được \(0 = \frac{{\sqrt {{2^2} - 4.2 + 4} }}{2}\) : thỏa mãn. Chọn B.

Câu 3. Cho hàm số \(y = f(x) = | - 5x|\). Khẳng định nào sau đây là sai?

A. \(f( - 1) = 5\).

B. \(f(2) = 10\).

C. \(f( - 2) = 10\).

D. \(f\left( {\frac{1}{5}} \right) =  - 1\).

Lời giải. Ta có  đúng.

- \(f(2) = | - 5.2| = |10| = 10 \to B\) đúng.

- \(f( - 1) = | - 5 \cdot ( - 2)| = |10| = 10 \to \) C đúng.

- \(f\left( {\frac{1}{5}} \right) = \left| { - 5 \cdot \frac{1}{5}} \right| = | - 1| = 1 \to \) D sai. Chọn \({\rm{D}}\).

Cách khác: Vì hàm đã cho là hàm trị tuyệt đối nên không âm. Do đó \({\rm{D}}\) sai.

Câu 4. Cho hàm số $f\left(x\right)=$$\left\{\begin{array}{l}\frac{2}{x-1}\\ \sqrt{x+1}\\ x^2-1\end{array}\right.$$\begin{array}{l}x\in (-\infty ;0)\\ x\in [0;2]\\ x\in (2;5]\end{array}$. Tính \(f(4)\)

A. \(f(4) = \frac{2}{3}\).

B. \(f(4) = 15\).

C. \(f(4) = \sqrt 5 \).

D. Không tính được.

Lời giải. Do \(4 \in (2;5]\) nên \(f(4) = {4^2} - 1 = 15\). Chọn \({\bf{B}}\).

Câu 5. Cho hàm số $f\left(x\right)=$$\left\{\begin{array}{l}\frac{2\sqrt{x+2}-3}{x-1}\\ x^2+1\end{array}\right.$$\begin{array}{l}x\ge 2\\ x<2\end{array}$. Tính \(P = f(2) + f( - 2)\).

A. \(P = \frac{8}{3}\).

B. \(P = 4\).

C. \(P = 6\).

D. \(P = \frac{5}{3}\).

Lời giải. Khi \(x \ge 2\) thì \(f(2) = \frac{{2\sqrt {2 + 2}  - 3}}{{2 - 1}} = 1\).

Khi \(x < 2\) thì \(f( - 2) = {( - 2)^2} + 1 = 5\).

Vậy \(f(2) + f( - 2) = 6\). Chọn C.

Vấn đề 2. Tìm tập xác đinh của hàm số

Câu 6. Tìm tập xác định D của hàm số \(y = \frac{{3x - 1}}{{2x - 2}}\).

A. \({\rm{D}} = \mathbb{R}\).

B. \({\rm{D}} = (1; + \infty )\).

C. \({\rm{D}} = \mathbb{R}\backslash \{ 1\} \).

D. \({\rm{D}} = [1; + \infty )\).

Lời giải. Hàm số xác định khi \(2x - 2 \ne 0 \Leftrightarrow x \ne 1\).

Vậy tập xác định của hàm số là \({\rm{D}} = \mathbb{R}\backslash \{ 1\} \). Chọn C.

Câu 7. Tìm tập xác định D của hàm số \(y = \frac{{2x - 1}}{{(2x + 1)(x - 3)}}\).

A. \({\rm{D}} = (3; + \infty )\).

B. \({\rm{D}} = \mathbb{R}\backslash \left\{ { - \frac{1}{2};3} \right\}\).

C. \({\rm{D}} = \left( { - \frac{1}{2}; + \infty } \right)\)

D. \({\rm{D}} = \mathbb{R}\).

Lời giải. Hàm số xác định khi \(\left\{ {\begin{array}{*{20}{l}}{2x + 1 \ne 0}\\{x - 3 \ne 0}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x \ne  - \frac{1}{2}{\rm{. }}}\end{array}} \right.} \right.\)

Vậy tập xác định của hàm số là \({\rm{D}} = \mathbb{R}\backslash \left\{ { - \frac{1}{2};3} \right\}\). Chọn \({\bf{B}}\).

Câu 8. Tìm tập xác định D của hàm số \(y = \frac{{{x^2} + 1}}{{{x^2} + 3x - 4}}\).

A. \({\rm{D}} = \{ 1; - 4\} \).

B. \({\rm{D}} = \mathbb{R}\backslash \{ 1; - 4\} \).

C. \({\rm{D}} = \mathbb{R}\backslash \{ 1;4\} \).

D. \({\rm{D}} = \mathbb{R}\).

Lời giải. Hàm số xác định khi

\({x^2} + 3x - 4 \ne 0 \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x \ne 1}\\{x \ne  - 4}\end{array}} \right.\).

Vậy tập xác định của hàm số là \({\rm{D}} = \mathbb{R}\backslash \{ 1; - 4\} \). Chọn \({\bf{B}}\).

Câu 9. Tìm tập xác định D của hàm số \(y = \frac{{x + 1}}{{(x + 1)\left( {{x^2} + 3x + 4} \right)}}\).

A. \({\rm{D}} = \mathbb{R}\backslash \{ 1\} \).

B. \({\rm{D}} = \{  - 1\} \).

C. \({\rm{D}} = \mathbb{R}\backslash \{  - 1\} \).

D. \({\rm{D}} = \mathbb{R}\).

Lời giải. Hàm số xác định khi

\(\left\{ {\begin{array}{*{20}{l}}{x + 1 \ne 0}\\{{x^2} + 3x + 4 \ne 0}\end{array} \Leftrightarrow x \ne  - 1} \right.\).

Vậy tập xác định của hàm số là \({\rm{D}} = \mathbb{R}\backslash \{  - 1\} \). Chọn \({\bf{C}}\).

Câu 10. Tìm tập xác định D của hàm số \(y = \frac{{2x + 1}}{{{x^3} - 3x + 2}}\).

A. \({\rm{D}} = \mathbb{R}\backslash \{ 1\} \).

B. \({\rm{D}} = \mathbb{R}\backslash \{  - 2;1\} \).

C. \({\rm{D}} = \mathbb{R}\backslash \{  - 2\} \).

D. \({\rm{D}} = \mathbb{R}\).

Lời giải. Hàm số xác định khi

\({x^3} - 3x + 2 \ne 0 \Leftrightarrow (x - 1)\left( {{x^2} + x - 2} \right) \ne 0\)

\( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x - 1 \ne 0}\\{{x^2} + x - 2 \ne 0}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x \ne 1}\\{\{ \begin{array}{*{20}{l}}{x \ne 1}\\{x \ne  - 2}\end{array}}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x \ne 1}\\{x \ne  - 2}\end{array}.} \right.} \right.} \right.\)

Vậy tập xác định của hàm số là \({\rm{D}} = \mathbb{R}\backslash \{  - 2;1\} \) Chọn \({\rm{B}}\).

Câu 11. Tìm tập xác định D\({\rm{D}}\) của hàm số \(\sqrt {x + 2}  - \sqrt {x + 3} \).

A. \({\rm{D}} = [ - 3; + \infty )\).

B. \({\rm{D}} = [ - 2; + \infty ).\quad \)

C. \({\rm{D}} = \mathbb{R}\).

D. \({\rm{D}} = [2; + \infty )\).

Lời giải. Hàm số xác định khi

 \(\left\{ {\begin{array}{*{20}{l}}{x + 2 \ge 0}\\{x + 3 \ge 0}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x \ge  - 2}\\{x \ge  - 3}\end{array} \Leftrightarrow x \ge  - 2} \right.} \right.\).

Vậy tập xác định của hàm số là \({\rm{D}} = [ - 2; + \infty )\). Chọn \({\rm{B}}\).

Câu 12. Tìm tập xác định D của hàm số \(y = \sqrt {6 - 3x}  - \sqrt {x - 1} \).

A. \({\rm{D}} = (1;2)\).

B. \({\rm{D}} = [1;2]\).

C. \({\rm{D}} = [1;3]\).

D. \({\rm{D}} = [ - 1;2]\).

Lời giải. Hàm số xác định khi

 \(\left\{ {\begin{array}{*{20}{l}}{6 - 3x \ge 0}\\{x - 1 \ge 0}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x \le 2}\\{x \ge 1}\end{array} \Leftrightarrow 1 \le x \le 2} \right.} \right.\).

Vậy tập xác định của hàm số là \({\rm{D}} = [1;2]\). Chọn \({\bf{B}}\).

Câu 13. Tìm tập xác định D của hàm số \(y = \frac{{\sqrt {3x - 2}  + 6x}}{{\sqrt {4 - 3x} }}\).

A. \({\rm{D}} = \left[ {\frac{2}{3};\frac{4}{3}} \right)\).

B. \({\rm{D}} = \left[ {\frac{3}{2};\frac{4}{3}} \right)\).

C. \({\rm{D}} = \left[ {\frac{2}{3};\frac{3}{4}} \right)\).

D. \({\rm{D}} = \left( { - \infty ;\frac{4}{3}} \right)\).

Lời giải. Hàm số xác định khi

\(\left\{ {\begin{array}{*{20}{l}}{3x - 2 \ge 0}\\{4 - 3x > 0}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x \ge \frac{2}{3}}\\{x < \frac{4}{3}}\end{array} \Leftrightarrow \frac{2}{3} \le x < \frac{4}{3}} \right.} \right.\).

Vậy tập xác định của hàm số là \({\rm{D}} = \left[ {\frac{2}{3};\frac{4}{3}} \right)\). Chọn \({\rm{B}}\).

Câu 14. Tìm tập xác định D của hàm số \(y = \frac{{x + 4}}{{\sqrt {{x^2} - 16} }}\).

A. \({\rm{D}} = ( - \infty ; - 2) \cup (2; + \infty )\).

B. \({\rm{D}} = \mathbb{R}\).

C. \({\rm{D}} = ( - \infty ; - 4) \cup (4; + \infty )\).

D. \({\rm{D}} = ( - 4;4)\).

Lời giải. Hàm số xác định khi

\({x^2} - 16 > 0 \Leftrightarrow {x^2} > 16 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x > 4}\\{x <  - 4}\end{array}} \right.\)

Vậy tập xác định của hàm số là \({\rm{D}} = ( - \infty ; - 4) \cup (4; + \infty )\). Chọn \({\rm{C}}\).

Câu 15. Tìm tập xác định D của hàm số \(y = \sqrt {{x^2} - 2x + 1}  + \sqrt {x - 3} \).

A. \({\rm{D}} = ( - \infty ;3]\).

B. \({\rm{D}} = [1;3]\).

C. \({\rm{D}} = [3; + \infty )\).

D. \({\rm{D}} = (3; + \infty )\).

Lời giải. Hàm số xác định khi

\(\left\{ {\begin{array}{*{20}{l}}{{x^2} - 2x + 1 \ge 0}\\{x - 3 \ge 0}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{{{(x - 1)}^2} \ge 0}\\{x - 3 \ge 0}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x \in \mathbb{R}}\\{x \ge 3}\end{array} \Leftrightarrow x \ge 3} \right.} \right.} \right.\).

Vậy tập xác định của hàm số là \({\rm{D}} = [3; + \infty )\). Chọn C.

Câu 16. Tìm tập xác định D của hàm số \(y = \frac{{\sqrt {2 - x}  + \sqrt {x + 2} }}{x}\).

A. \({\rm{D}} = [ - 2;2]\).

B. \({\rm{D}} = ( - 2;2)\backslash \{ 0\} \).

C. \({\rm{D}} = [ - 2;2]\backslash \{ 0\} \).

D. \({\rm{D}} = \mathbb{R}\).

Lời giải. Hàm số xác định khi

\(\left\{ {\begin{array}{*{20}{l}}{2 - x \ge 0}\\{x + 2 \ge 0}\\{x \ne 0}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x \le 2}\\{x \ge  - 2}\\{x \ne 0}\end{array}} \right.} \right.\).

Vậy tập xác định của hàm số là \({\rm{D}} = [ - 2;2]\backslash \{ 0\} \). Chọn C.