Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu Dấu của đa thức bậc nhất và bậc hai trong chương trình lớp 10, tài liệu bao gồm 251 trang. Tài liệu được tổng hợp từ các tài liệu ôn thi hay nhất giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kỳ thi sắp hới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.
Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây
Tài liệu bao gồm các nội dung sau:
Dấu nhị thức bậc nhất
Tam thức bậc hai
Bài tập
Dấu của đa thức bậc nhất và bậc hai trong chương trình lớp 10
Chương 1
Dấu của đa thức
1.1 Dấu nhị thức bậc nhất
Định nghĩa 1.1. Nhị thức bạcc nhất theo biến x là biểu thức có dạng f(x) = ax +b \((a \ne 0)\).
Định lí 1.1. Dấu f(x) = ax +b cùng dấu a nếu \(x > - \frac{b}{a}\) và trái dấu a nếu \(x < \frac{b}{a}\)
Ví dụ 1.1. Xét dấu nhị thức f(x) = x - 2.
Lời giải. Nghiệm của f(x) là x = 2.
Bảng xét dấu.
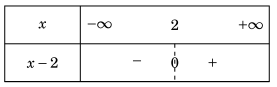
Từ bảng xét dấu, ta có
- \(f(x) > 0 \Leftrightarrow x \in (2, + \infty )\);
- \(f(x) < 0 \Leftrightarrow x \in ( - \infty ,2)\).
Ví dụ 1.2. Xét dấu nhị thức \(f(x) = 3 - 4x\).
Lời giải. Nghiệm của f(x) là \(x = \frac{3}{4}\). Hệ số của x là -4.
Bảng xét dấu.
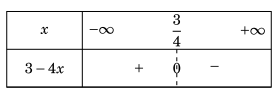
Từ bảng xét dấu, ta có
- \(f(x) > 0 \Leftrightarrow x \in \left( { - \infty ,\frac{3}{4}} \right)\)
- \(f(x) < 0 \Leftrightarrow x \in \left( {\frac{3}{4}, + \infty } \right)\).
1.1.1 Dấu tích các nhị thức bậc nhất
Ví du 1.3. Xét dấu \(f(x) = (x - 2)(3 - x)\).
Lời giải. Nghiệm của f(x) là x=2 và x=3.
Bảng xét dấu.
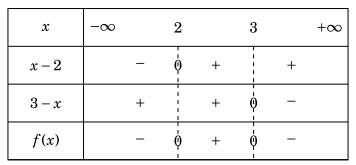
Ví dụ 1.4. Xét dấu của \(f(x) = (x + 2)\left( {{x^2} + 5x + 6} \right)\).
Lời giải. \(f(x) = {(x + 2)^2}(x + 3)\). Nghiệm của f(x) là \(x = - 2\) và \(x = - 3\).
Chú ý là với mọi x.
Bảng xét dấu.
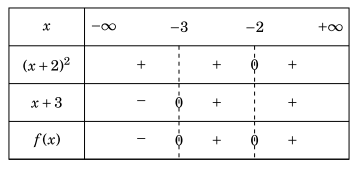
Từ bảng xét dấu, ta có
\(f(x) < 0 \Leftrightarrow x \in ( - \infty , - 3);f(x) > 0 \Leftrightarrow x \in ( - 3, + \infty )\backslash \{ - 2\} \).
1.1.2 Dấu thương các nhị thức bậc nhất
Ví dụ 1.5. Xét dấu \(f(x) = \frac{{x + 1}}{{x - 7}}\).
Lời giải. f(x) = 0 với x= -1 và f(x) không xác định tại x=7.
Bảng xét dấu.
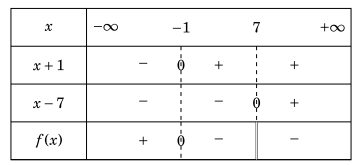
Ví dụ 1.6. Xét dấu của \(f(x) = \frac{1}{{x + 2}} - \frac{3}{{x + 4}}\).
Lời giải.
Ta có
\(f(x) = - \frac{{2(x + 1)}}{{(x + 2)(x + 4)}}.\)
\(f(x) = 0\) tại \(x = - 1\) và \(f(x)\) không xác định tại \(x = - 2\) và \(x = - 4\).
Bảng xét dấu của \(f(x)\) như sau:
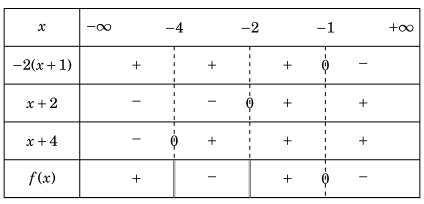
1.1.3 Ứng dụng xét dấu để giải bất phương trình
Ví dụ 1.7. Giải bất phương trình \((2x - 3)(4 - 5x) > 0\).
Lời giải. Đặt \(f(x) = (2x - 3)(5 - 4x)\).
Nhận thấy rằng \(f(x) = 0\) tại \(x = \frac{3}{2}\) hoặc \(x = \frac{5}{4}\).
Bảng xét dấu của f(x) như sau:
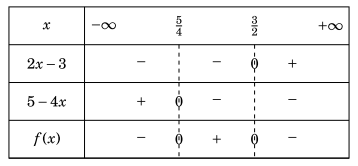
Dựa vào bảng xét dấu, tập nghiệm bất phương trình đã cho là \(\left( {\frac{5}{4},\frac{3}{2}} \right)\).
Ví dụ 1.8. Giải bất phương trình .
Ta có
Đặt \(f(x) = (x + 5)(3x + 1)\).
Nhận thây rằng \(f(x) = 0\) tại \(x = - 5\) hoặc \(x = - \frac{1}{3}\).
Bảng xét dấu của f(x) như sau:
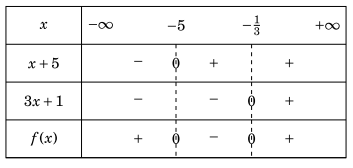
Dựa vào bảng xét dấu, tập nghiệm bất phương trình đã cho là \(( - \infty ; - 5] \cup \left[ { - \frac{1}{3}; + \infty } \right)\).
Ví dụ 1.9. Giải bất phương trình .
Lời giải. Ta có
Đặt \(f(x) = (x - 4)(x - 2)\). Bảng xét dâu của f(x) như sau:
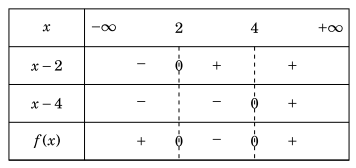
Ví dụ 1.10. Giải bất phương trình .
Lời giải. Điều kiện xác định của bât phương trình là .
Ta thấy x=4 là một nghiệm của bât phương trình đã cho.
Với \(x > 4\), thì \((x - 2)\sqrt {x - 4} > 0\), nên bất phương trình đã cho tương đương với hay
Vậy nghiệm bất phương trình đã cho là x = 4 hoặc .
Vi dụ 1.11.
Giải bât phương trình .
Lời giải. Điều kiện xác định của bât phương trình là .
Ta thây x = 4 là một nghiệm của bất phương trình đã cho.
Với \(x > 4\), từ bất phương trình đã cho, suy ra
\((x - 5)(9 - x) > 0 \Leftrightarrow 5 < x < 9.\)
Vậy nghiệm bất phương trình đã cho là x = 4 hoặc \(5 < x < 9\).
Ví dụ 1.12. Giải bất phương trình \(\frac{1}{x} > 1\).
Lời giải. Ta có
\(\frac{1}{x} > 1 \Leftrightarrow \frac{1}{x} - 1 > 0 \Leftrightarrow \frac{{1 - x}}{x} > 0\)
Đặt \(f(x) = \frac{{1 - x}}{x}\).
f(x)=0 tại x=1 và f(x) không xác định tại x=0.
Dựa vào bảng xét dấu, tập nghiệm bất phương trình đã cho là (0;1).
Lời bình. Không viết bất phương trình
\(\frac{1}{x} > 1 \Leftrightarrow 1 > x.\)
Vì ta chưa biết dấu của x.
Cũng có thể làm như sau: Nhận thây không là nghiệm của bất phương trình. Với x >0, bất phương trình tương đương với 1 > x.
Vậy nghiệm của bất phương trình là 0 < x < 1.
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
