Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu Chuyên đề hàm số bậc nhất và hàm số bậc 2 - Đại số 10, tài liệu bao gồm 81 trang. Tài liệu được tổng hợp từ các tài liệu ôn thi hay nhất  giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kỳ thi sắp hới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây

Chuyên đề hàm số bậc nhất và hàm số bậc 2 - Đại số 10

Chương 2: Hàm số bậc nhất và hàm số bậc hai

CHUYÊN ĐỀ 1: Hàm số

Phần I. Trọng tâm cần luyện

+ Biểu diễn được các điểm trên mặt phẳng tọa độ.

+ Tính toán được giá trị của hàm số tại một điểm cho trước, tìm tập xác định. Tìm tập giá trị, giá trị lớn nhất, giá trị nhỏ nhất của hàm số đơn giản, khoảng cách giũa hai điểm trên mặt phẳng tọa độ.

+ Xét được sự đồng biến, nghịch biến, tính chẵn - lẻ của một số hàm số đơn giản.

I. Lí thuyết trọng tâm

Khái niệm về hàm số

Ví dụ: \(y = {x^2}\).

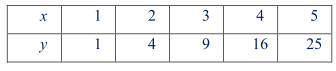
- Cho hai đại lượng biến thiên x và y, trong đó x nhận giá trị thuộc tập số . Khi đó đại lượng y được gọi là hàm số của đại lượng x nếu:

Đại lượng y phụ thuộc vào đại lượng x thay đổi.

Với mỗi giá trị của \(x \in D\) ta luôn xác định được một và chỉ một giá trị tương ứng của .

- Hàm số có thể được cho bằng bảng hoặc công thức.

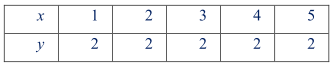
Ví dụ: Hàm hằng \(y = 2\).

- Khi hàm số được cho bởi công thức \(y = f(x)\) thì biến số x chỉ lấy những giá trị làm cho f(x) xác định.

- Khi x thay đổi mà y luôn nhận giá trị không đổi thì hàm số y được gọi là hàm hằng.

Đồ thị của hàm số

Ví dụ: Hàm số \(y = 2x - 1\) có đồ thị như hình vẽ.

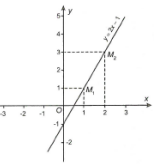
Cho hàm số \(y = f(x)\) có tập xác định \(D\).

Đồ thị của hàm số \(y = f(x)\) là tập hợp tất cả các điểm \(M\left( {{x_0};{y_0}} \right)\) trên hệ trục tọa độ Oxy thỏa mãn \({x_0} \in D\) và \({y_0} \in f\left( {{x_0}} \right)\).

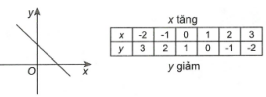
Sự biến thiên của hàm số

Cho hàm số \(y = f(x)\) xác định trên K.

- Hàm số \(y = f(x)\) được gọi là đồng biến (hay tăng) trên K nếu\(\forall {x_1},{x_2} \in K,{x_1} < {x_2} \Rightarrow f\left( {{x_1}} \right) < f\left( {{x_2}} \right)\).

- Hàm số \(y = f(x)\) được gọi là nghịch biến (hay giảm) trên K \(\forall {x_1},{x_2} \in K,{x_1} < {x_2} \Rightarrow f\left( {{x_1}} \right) > f\left( {{x_2}} \right).\)

 Hàm số đồng biến

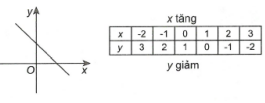
Hàm số nghịch biến

Khái niệm hàm số chẵn, hàm số lẻ

Cho hàm số \(y = f(x)\) với tập xác định \(D\).

Hàm số \(y = f(x)\) được gọi là hàm số chẵn nếu với mọi \(x \in D\), ta có \( - x\) cũng thuộc D và \(f( - x) = f(x)\).

Hàm số \(y = f(x)\) được gọi là hàm lẻ nếu mọi \(x \in D\), ta có \( - x\) cũng thuộc D và \(f( - x) =  - f(x)\).

Ví dụ: Hàm số \(f(x) = \sqrt {2 + x}  - \sqrt {2 - x} \) là hàm số lẻ vì:

Tập xác định của hàm số là \(D = [ - 2;2]\) nên dễ thấy \(\forall x \in [ - 2;2] \Rightarrow  - x \in [ - 2;2]\) và \(f( - x) = \sqrt {2 - x}  - \sqrt {2 + x}  =  - f(x)\)

Đồ thị của hàm số chăn và hàm số lẻ

- Đồ thị của hàm số chẵn nhận trục tung làm trục đối xúng.

- Đồ thị của hàm số lẻ nhận gốc tọa độ làm  tâm đối xúng.

Ví dụ:

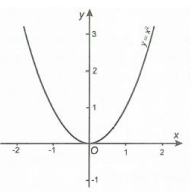
Đồ thị hàm số chãn \(y = {x^2}\) nhận trục Oy làm trục đối xứng.

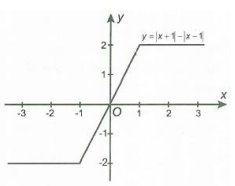
Đồ thị hàm số lẻ \(y = |x + 1| - |x - 1|\) nhận gốc tọa đối xứng.

II. Các dạng bài tập

Dạng 1: Tính giá trị của hàm số tại một điểm

* Phương pháp giải

Để tính giá trị của hàm số \(y = f(x)\) tại \({x_0}\), ta thay \(x = {x_0}\) vào \(y = f(x)\) ta được \({y_0} = f\left( {{x_0}} \right).\).

Ví dụ: Cho hàm số \(y = f(x) = 3\sqrt x  - 2\). Tính f(1).

Hướng dẫn giải

Thay \(x = 1\) vào biểu thức của hàm số

\(f(1) = 3\sqrt 1  - 2 = 1.{\rm{ }}\)

Ví dụ mẫu

Ví dụ 1: Cho \[y = f(x) = \frac{1}{2}x\].Tính các giá trị của biểu thức \(f(0) + f( - 6) - f(2)\).

Hướng dấn giải

Ta có \(f(0) = \frac{1}{2} \cdot 0 = 0,f(2) = \frac{1}{2} \cdot 2 = 1,f( - 6) = \frac{1}{2} \cdot ( - 6) =  - 3\).

Vậy \(f(0) + f( - 6) - f(2) = 0 - 3 - 1 =  - 4\).

Ví dụ 2: Cho \(y = f(x) = \sqrt {2x + 1} \). Tính các giá trị của biểu thức \(f(f(0))\).

Hướng dấn giải

Ta có \(f(0) = \sqrt {2.0 + 1}  = 1\) và \(f(f(0)) = f(1) = \sqrt {2.1 + 1}  = \sqrt 3 \).

Ví dụ 3: Một chất điểm chuyển động biến đổi đều với vận tốc \(v = 5t + 3(\;{\rm{cm}}/{\rm{s}})\), thời gian \(t \ge 0\) đo bằng giây. Khi đó vận tốc v là hàm số theo biến t.

a) Hãy tính các giá trị của v theo các giá trị của t rồi hoàn thành bảng sau

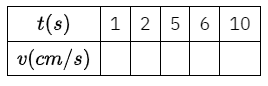
b) Tại thời điểm nào chất điểm đạt vận tốc \(v = 38(\;{\rm{cm}}/{\rm{s}})\).

Hướng dấn giải

a) Với mỗi giá trị t\(t\) ta sẽ xác định được duy nhất một giá trị của v là \(v = 5t + 3\).

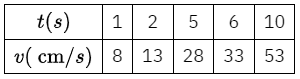
b) Với \(v = 38\) thì \(5t + 3 = 38 \Leftrightarrow t = 7\).

Vậy chất điểm đạt vận tốc \(v = 38(\;{\rm{cm}}/{\rm{s}})\) tại thời diểm \(t = 7(\;{\rm{s}})\).

Ví dụ 4:

a) Cho hàm số \(f(x) = 4x\). Giá trị nào lớn nhất trong các giá trị sau?

A. \(f( - 1)\).

B. \(f(0)\).

C. \(f\left( {\frac{1}{2}} \right)\).

D. \(f\left( { - \frac{3}{4}} \right)\).

b) Cho hàm số \(g(x) = 4x - 5\). Giá trị nào nhỏ nhất trong các giá trị sau?

A. \(g( - 1)\).

B. \(g(0)\).

C. \(g\left( {\frac{1}{2}} \right)\).

D. \(g\left( { - \frac{3}{4}} \right)\).

Hướng dấn giải

a) Ta có

\(\begin{array}{l}f( - 1) = 4 \cdot ( - 1) =  - 4,\\f(0) = 4 \cdot 0 = 0,\\f\left( {\frac{1}{2}} \right) = 4 \cdot \frac{1}{2} = 2,\\f\left( { - \frac{3}{4}} \right) = 4 \cdot \left( { - \frac{3}{4}} \right) =  - 3.\end{array}\)

Chọn C.

b) Ta có

\[\begin{array}{l}g( - 1) = 4 \cdot ( - 1) - 5 =  - 9,\\g(0) = 4 \cdot 0 - 5 =  - 5\end{array}\]

\[\begin{array}{l}g\left( {\frac{1}{2}} \right) = 4 \cdot \frac{1}{2} - 5 =  - 3,\\g\left( { - \frac{3}{4}} \right) = 4 \cdot \left( { - \frac{3}{4}} \right) - 5 =  - 8\end{array}\]

Chọn A.

Nhận xét: Từ những tính toán trên ta thấy

\(\begin{array}{l}f( - 1) > g( - 1),f(0) > g(0),\\f\left( {\frac{1}{2}} \right) > g\left( {\frac{1}{2}} \right){\rm{ va}}\,{\rm{ }}f\left( { - \frac{3}{4}} \right) > g\left( { - \frac{3}{4}} \right){\rm{. }}\end{array}\)

Ta có thể chứng minh được rằng với mọi giá trị  thì \(f(x) > g(x)\).

Ví dụ 5. Cho hàm số \(f(x) = \left\{ {\begin{array}{*{20}{l}}{x - 3{\rm{ khi }}x \ge 2}\\{2x + 1{\rm{ khi }}x < 2}\end{array}} \right.\). Giá trị của \(f(x)\) tại điểm \(x = 1\) bằng

A. 3 .

B. \( - 2\).

C. 5 .

D. 1 .

Hướng dấn giải

Vì \(x = 1 < 2\) nên giá trị của \(f(x)\) tại \(x = 1\) là giá trị của hàm số \(f(x) = 2x + 1\) tại \(x = 1\).

Khi đó \(f(1) = 2.1 + 1 = 3\).

Chọn A.

Ví dụ 6. Cho \(y = f(x)\) xác định trên  và thỏa mãn \(f(x) + 3f\left( {\frac{1}{x}} \right) = 2x - 1,\forall x \ne 0\). Tính \(f(2)\).

Hướng dấn giải

Cách 1. Thay \(x = 2\) vào đẳng thức đề bài, ta có

\(f(2) + 3f\left( {\frac{1}{2}} \right) = 3.\)(1)

Thay \(x = \frac{1}{2}\) vào đẳng thứ đề bài, ta có

\(f\left( {\frac{1}{2}} \right) + 3f(2) = 0 \Leftrightarrow  - 9f(2) - 3f\left( {\frac{1}{2}} \right) = 0.\)(2)

Cộng hai đẳng thức (1) và (2) vế với vế, ta thu được --8 f(2)=3.

Vậy \(f(2) =  - \frac{3}{8}\).

Cách 2 .

Thay x bởi \(\frac{1}{x}\) thì đẳng thức đề bài trở thành ta có \(f\left( {\frac{1}{x}} \right) + 3f(x) = \frac{2}{x} - 1,\forall x \ne 0\).

Ta có:

\[\begin{array}{l}\left\{ {\begin{array}{*{20}{l}}{f(x) + 3f(\frac{1}{x}) = 2x - 1,\forall x \ne 0}\\{f(\frac{1}{x}) + 3f(x) = \frac{2}{x} - 1,\forall x \ne 0}\end{array}} \right.\\ \Rightarrow \left\{ {\begin{array}{*{20}{l}}{f(x) + 3f\left( {\frac{1}{x}} \right) = 2x - 1,\forall x \ne 0}\\{ - 3f\left( {\frac{1}{x}} \right) - 9f(x) = 3 - \frac{6}{x},\forall x \ne 0}\end{array}} \right.\end{array}\]

\[ \Rightarrow  - 8f(x) = 2x + 2 - \frac{6}{x},\forall x \ne 0\]

Từ đó tính được \(f(x) =  - \frac{1}{4}x - \frac{1}{4} + \frac{3}{{4x}},\forall x \ne 0\)

Vậy \(f(2) =  - \frac{1}{4} \cdot 2 - \frac{1}{4} + \frac{3}{{4 \cdot 2}} =  - \frac{3}{8}\).

Nhận xét: Về bản chất, cả hai cách làm tương tự nhau. Tuy nhiên cách 1 chỉ tính được giá trị của hàm số tại điểm \(x = 2\), trong khi cách 2 tìm được biểu thức của \(f(x)\) với mọi \(x \ne 0\).

* Bài tập tự luyện dạng 1

Bài tập cơ bản

Câu 1: Biểu đồ dưới đây (trích từ báo Khoa học và Đời sống số 47 ngày 8-11-2002) mô tả số công trình khoa học kĩ thuật đăng kí dự giải thưởng Sáng tạo Khoa học Công nghệ Việt Nam và số công trình đoạt giải hằng năm từ 1995 đến 2001. Gọi \(f(x)\) là tỉ số giữa số công trình đoạt giải thưởng trên tổng số công trình tham dự giải thưởng của năm x. Ta có hàm số \(y = f(x)\) với tập xác định là \(D = \{ 1995,1996,1997,1998,1999,2000,2001\} \). Trong các khẳng định sau, khẳng định nào sai?

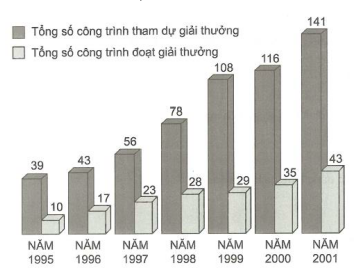
A. \[f(1995) = \frac{{10}}{{39}}\]

B. \[f(1996) = \frac{{17}}{{43}}\]

C. \[f(1999) = \frac{{23}}{{56}}\]

D. \[f(2001) = \frac{{43}}{{141}}\]