Tailieumoi.vn xin giới thiệu tới bạn đọc tài liệu về Cách tìm tập xác định của hàm số và ví dụ minh họa, chi tiết nhất, tài liệu gồm đầy đủ về lý thuyết Cách tìm tập xác định của hàm số và ví dụ minh họa, giúp các bạn củng cố kiến thức, học tốt môn Toán hơn.

Cách tìm tập xác định của hàm số và ví dụ minh họa

A. Lý thuyết Tập xác định của hàm số

• Hàm số được cho bằng bảng: Với mọi x ∈ D, ta xác định được một và chỉ một giá trị của y tương ứng thì y là hàm số của x và tập D là tập xác định của hàm số.

• Hàm số được cho bằng công thức:

Tập xác định của hàm số y = f(x) là tập hợp tất cả các số thực x sao cho biểu thức f(x) có nghĩa.

Một số hàm số thường gặp và tập xác định của chúng:

+ Loại 1: Hàm số là một đa thức biến x (không chứa căn thức và phân thức) thì tập xác định là D = ℝ.

Chẳng hạn, hàm số bậc nhất y = ax + b và hàm số bậc hai y = ax² + bx + c (a ≠ 0) thì tập xác đinh là D = ℝ.

+ Loại 2: Hàm số là phân thức (chứa ẩn ở mẫu). Hàm số xác định khi mẫu khác 0.

Hàm số y = f(x) = $\frac{1}{B\left(x\right)}$ hoặc y = f(x) = $\frac{A\left(x\right)}{B\left(x\right)}$ xác định khi và chỉ khi B(x) ≠ 0.

+ Loại 3: Hàm số chứa căn thức. Hàm số khác định khi biểu thức trong căn lớn hơn hoặc bằng 0, nếu căn thức ở dưới mẫu, biểu thức trong căn phải lớn hơn không.

$\sqrt{A\left(x\right)}$ có nghĩa khi và chỉ khi A(x) ≥ 0.

$\frac{1}{\sqrt{B\left(x\right)}}$ hoặc $\frac{A\left(x\right)}{\sqrt{B\left(x\right)}}$ có nghĩa khi và chỉ khi B(x) > 0.

$\frac{\sqrt{A\left(x\right)}}{\sqrt{B\left(x\right)}}$ có nghĩa khi và chỉ khi .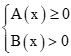

B. Bài tập Tìm tập xác định của hàm số

Bài tập vận dụng

Bài 1. Tìm tập xác định của các hàm số sau:

a) $y=\frac{x^2+5}{x^2+3x-4}$

b) $y=\frac{2x+3}{\left(x+1\right)\left(x^2+5x+6\right)}$

Hướng dẫn giải

a) ĐKXĐ: x² - 3x + 4 ≠ 0 nên $\left\{\begin{array}{c}x\ne 1\\ x\ne -4\end{array}\right.$.

Suy ra tập xác định của hàm số là D = ℝ\{1; –4}.

b) ĐKXĐ: (x + 1)(x² + 5x + 6) ≠ 0 nên $\left\{\begin{array}{c}x\ne -1\\ x\ne -2\\ x\ne -3\end{array}\right.$.

Suy ra tập xác định của hàm số là D = ℝ\{–1; –2; –3}.

Bài 2. Tìm tập xác định của các hàm số sau:

a) $y=\frac{2x^2+3x+2}{x^3+x^2-5x-2}$

b) $y=\frac{x+6}{{\left(x-1\right)}^2-2x^2}$

Hướng dẫn giải

a) ĐKXĐ: x³ + x² - 5x - 2 ≠ 0 nên $\left\{\begin{array}{c}x\ne 2\\ x\ne \frac{-3\pm \sqrt{5}}{2}\end{array}\right.$

Suy ra tập xác định của hàm số là $D=ℝ\backslash \left\{-2;\frac{-3\pm \sqrt{5}}{2}\right\}$.

b) ĐKXĐ: ${\left(x-1\right)}^2-2x^2\ne 0$

$\iff \left(x^2-\sqrt{2}x-1\right)\left(x^2+\sqrt{2}x-1\right)\ne 0$

$\iff \left\{\begin{array}{c}x\ne \frac{\sqrt{2}\pm \sqrt{7}}{2}\\ x\ne \frac{-\sqrt{2}\pm \sqrt{7}}{2}\end{array}\right.$

Suy ra tập xác định của hàm số là $D=ℝ\backslash \left\{\frac{\sqrt{2}\pm \sqrt{7}}{2};\frac{-\sqrt{2}\pm \sqrt{7}}{2}\right\}$

Bài 3. Tìm tập xác định của các hàm số sau:

a) $y=\frac{x+1}{\sqrt{3x+2}}$

b) $y=\frac{\sqrt{x+2}}{\left(x+3\right)\sqrt{x^2-4x+4}}$

Hướng dẫn giải

a) ĐKXĐ: 3x + 2 > 0 hay x > $-\frac{2}{3}$.

Suy ra tập xác định của hàm số là D = $\left(-\frac{2}{3};\infty \right)$.

b) ĐKXĐ: $\left\{\begin{array}{c}x+3\ne 0\\ x^2-4x+4>0\end{array}\right.$ hay $\left\{\begin{array}{c}x\ne -3\\ x\ne 2\end{array}\right.$.

Suy ra tập xác định của hàm số là D = ℝ\{2; –3}.

Bài 4. Tìm tập xác định của các hàm số sau:

a) $y=\frac{\sqrt{5-3\left|x\right|}}{x^2+4x+3}$

b) $y=\frac{x+5}{\sqrt{x^2-25}}$

Hướng dẫn giải

a) ĐKXĐ: $x^2+4x+3\ne 0$

$\iff \left\{\begin{array}{c}x\ne -1\\ x\ne -3\end{array}\right.$

Suy ra tập xác định của hàm số là D = ℝ\{–1; –3}.

b) ĐKXĐ: x² - 25 > 0 nên x < –5 hoặc x > 5

Suy ra tập xác định của hàm số là D = (–∞; –5) ∪ (5; +∞).

Bài 5. Tìm tập xác định của các hàm số sau:

a) $y=\sqrt{x+5}-\sqrt{x+7}$

b) $y=\frac{\sqrt[3]{x^2-1}}{x^2-2x+3}$

Hướng dẫn giải

a) ĐKXĐ: $\left\{\begin{array}{c}x+5\ge 0\\ x+7\ge 0\end{array}\right.$ nên x ≥ -5

Suy ra tập xác định của hàm số là D = [–5; +∞).

b) ĐKXĐ: $x^2-2x+3\ne 0$

Hàm số $x^2-2x+3>0\forall x$

Suy ra tập xác định của hàm số là ℝ.

Bài 6. Tìm tập xác định của các hàm số sau

Hướng dẫn:

a) ĐKXĐ: x² + 3x - 4 ≠ 0

Suy ra tập xác định của hàm số là D = R\{1; -4}.

b) ĐKXĐ:

c) ĐKXĐ: x³ + x² - 5x - 2 = 0

Suy ra tập xác định của hàm số là

d) ĐKXĐ: (x² - 1)² - 2x² ≠ 0 ⇔ (x² - √2.x - 1)(x² + √2.x - 1) ≠ 0

Suy ra tập xác định của hàm số là:

Bài 7.  Tìm tập xác định của các hàm số sau:

Hướng dẫn:

a) ĐKXĐ: 

Suy ra tập xác định của hàm số là D = (1/2; +∞)\{3}.

b) ĐKXĐ: 

Suy ra tập xác định của hàm số là D = [-2; +∞)\{0;2}.

c) ĐKXĐ:

Suy ra tập xác định của hàm số là D = [-5/3; 5/3]\{-1}

d) ĐKXĐ: x² - 16 > 0 ⇔ |x| > 4

Suy ra tập xác định của hàm số là D = (-∞; -4) ∪ (4; +∞).

Bài 8.  Cho hàm số: 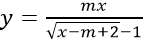 với m là tham số

a) Tìm tập xác định của hàm số theo tham số m.

b) Tìm m để hàm số xác định trên (0; 1)

Hướng dẫn:

a) ĐKXĐ:

Suy ra tập xác định của hàm số là D = [m-2; +∞)\{m-1}.

b) Hàm số xác định trên (0; 1) ⇔ (0;1) ⊂ [m - 2; m - 1) ∪ (m - 1; +∞)

Vậy m ∈ (-∞; 1] ∪ {2} là giá trị cần tìm.

Bài 9.  Cho hàm số 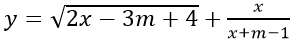 với m là tham số.

a) Tìm tập xác định của hàm số khi m = 1.

b) Tìm m để hàm số có tập xác định là [0; +∞)

Hướng dẫn:

ĐKXĐ: 

a) Khi m = 1 ta có ĐKXĐ: 

Suy ra tập xác định của hàm số là D = [(-1)/2; +∞)\{0}.

b) Với 1 - m ≥ (3m - 4)/2 ⇔ m ≤ 6/5, khi đó tập xác định của hàm số là

D = [(3m - 4)/2; +∞)\{1 - m}

Do đó m ≤ 6/5 không thỏa mãn yêu cầu bài toán.

Với m > 6/5 khi đó tập xác định của hàm số là D = [(3m - 4)/2; +∞).

Do đó để hàm số có tập xác định là [0; +∞) thì (3m - 4)/2 = 0 ⇔ m = 4/3 (thỏa mãn)

Vậy m = 4/3 là giá trị cần tìm.

Bài tập tự luyện

Bài 1. Tìm tập xác định của các hàm số sau:

a) $y=\left\{\begin{array}{c}\frac{x}{3}\text{ khi }x\ge 1\\ \sqrt{x+2}\text{ khi }x<1\end{array}\right.$

b) $y=\left\{\begin{array}{c}\frac{1}{x-5}\text{ khi }x\ge 1\\ \sqrt{x-5}\text{ khi }x<1\end{array}\right.$

Bài 2. Cho hàm số $y=\sqrt{2x-3m+4}+\frac{x}{x+m-1}$ với m là tham số.

a) Tìm tập xác định của hàm số khi m = 2.

b) Tìm m để hàm số có tập xác định là [0; +∞).

Bài 3. Tìm m để hàm số $y=\sqrt{x^2-mx+3}$ xác định trên (0; 3).

Bài 4. Tìm m để hàm số $y=\sqrt{x-m+1}+\frac{2x}{\sqrt{-x+2m}}$ xác định trên (–1; 3).

Bài 5. Tìm m để hàm số $y=\frac{\sqrt{x}}{\sqrt{x-m+1}}$ xác định trên [0; +∞).