Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu Dự đoán và chứng minh tính chất Oxy, tài liệu bao gồm 61 trang. Tài liệu được tổng hợp từ các tài liệu ôn thi hay nhất  giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kỳ thi sắp hới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây

Nội dung tài liệu bao gồm

Phần 1: Hình vuông

Dự đoán và chứng minh tính chất Oxy

HÌNH OXY: DỰ ĐOÁN VÀ VẺ ĐẸP CHỨNG MINH

Chuyên đề 1: Hình vuông

Bài 1: Trong mặt phẳng Oxy, cho hình vuông ABCD có \({\rm{A}}(4;6)\), gọi M,N lần lượt là các điểm nằm trên cạnh BC và CD sao cho , điểm \({\rm{M}}( - 4;0)\) và đường thẳng MN có phương trình \(11{\rm{x}} + 2{\rm{y}} + 44 = 0\). Tìm tọa độ các điểm B,C,D

DS: \(B(0; - 2),C( - 8;2),D( - 4;10)\)

Bài 2: Trong mặt phẳng Oxy, cho hình vuông ABCD có đỉnh C thuộc đường thẳng \({\rm{d}}:{\rm{x}} + 2{\rm{y}} - 6 = 0\), điểm M(1;1) thuộc cạnh BD biết rằng hình chiếu vuông góc của điểm M trên cạnh AB và AD đều nằm trên đường thẳng \(\Delta :{\rm{x}} + {\rm{y}} - 1 = 0\). Tìm tọa độ đỉnh C

ĐS: \(C(2;2)\)

Bài 3: Trong mặt phẳng Oxy, cho hình vuông ABCD có \(C(2; - 2)\). Gọi I, K lần lượt là trung điểm của DA và DC, \(M( - 1; - 1)\) là giao điểm của BI và AK. Tìm tọa độ các đỉnh còn lại của hình vuông ABCD biết B có hoành độ dương.

ĐS:\(A( - 2;0),B(1;1),D( - 1; - 3)\)

Bài 4: Trong mặt phẳng Oxy, cho hình vuông ABCD có điểm B thuộc đường thẳng \((d)2x - y = 0\). Điểm M(-3;0) là trung điểm AD, điểm \({\rm{K}}( - 2; - 2)\) thuộc cạnh DC sao cho KC = 3KD . Tìm tọa độ các đỉnh của hình vuông .

ĐS:\({\rm{A}}( - 3;2),{\rm{B}}(1;2),{\rm{C}}(1; - 2),{\rm{D}}( - 3; - 2)\)

Bài 5: Trong mặt phẳng Oxy, cho hình vuông ABCD có tâm I. Các điểm \(G\left( {\frac{{10}}{3};\frac{{11}}{3}} \right),E\left( {3; - \frac{2}{3}} \right)\) lần lượt là trong tâm của tam giác ABI và tam giác ADC. Xác định tọa độ các đỉnh hình vuông ABCD, biết A có tung độ nguyên

ĐS: \(A( - 1;4),B(7;6),C(9; - 2),D(1; - 4)\)

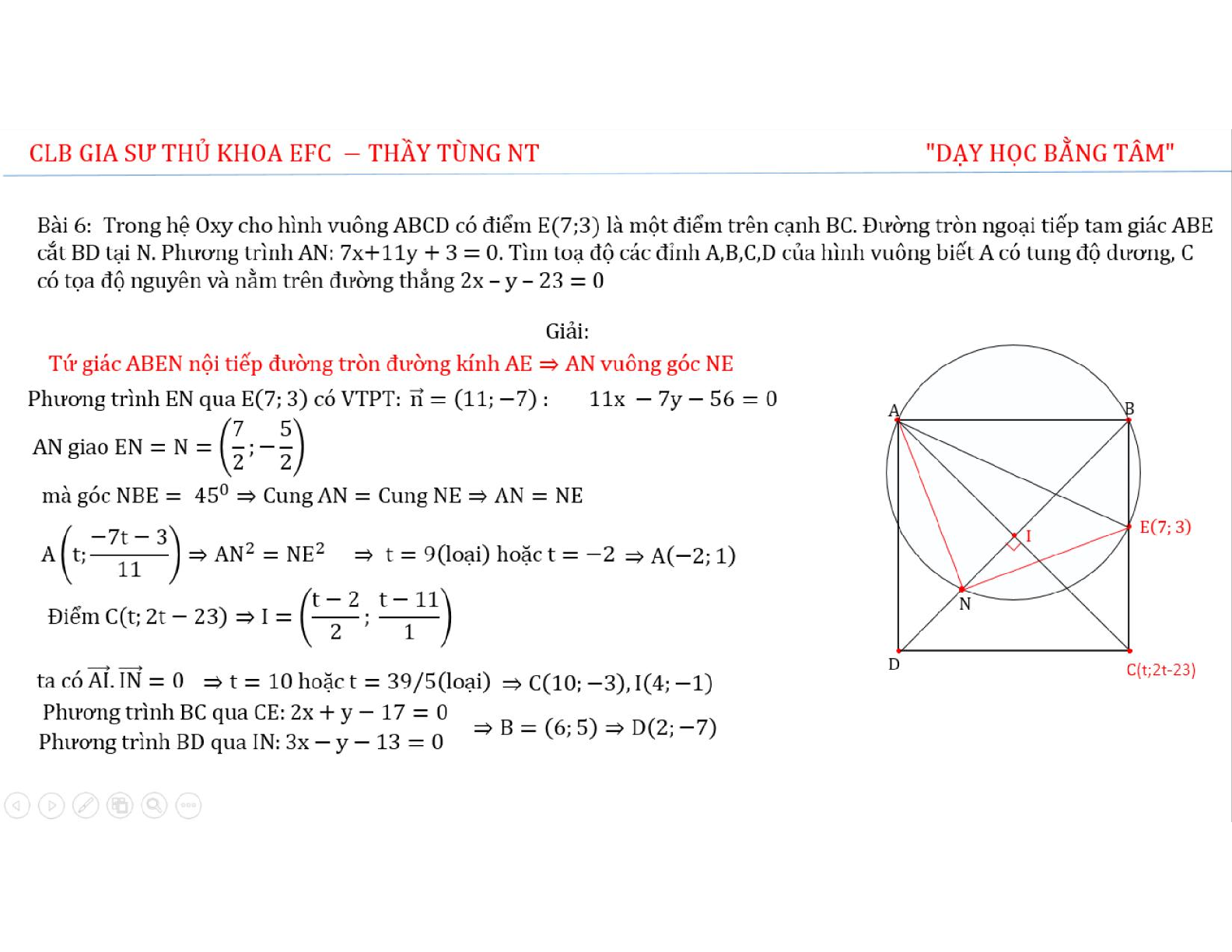
Bài 6: Trong hệ Oxy cho hình vuông ABCD có điểm E( 7;3) là một điểm trên cạnh BC. Đường tròn ngoại tiếp tam giác ABE cắt BD tại N. Phương trình \({\rm{AN}}:7{\rm{x}} + 11{\rm{y}} + 3 = 0\). Tìm toạ độ các đỉnh A,B,C,D của hình vuông biết A có tung độ dương, C có tọa độ nguyên và nằm trên đường thẳng \(2{\rm{x}} - {\rm{y}} - 23 = 0\)

ĐS: \({\rm{A}}( - 2;1),{\rm{B}}(6;5),{\rm{C}}(10; - 3),{\rm{D}}(2; - 7)\)

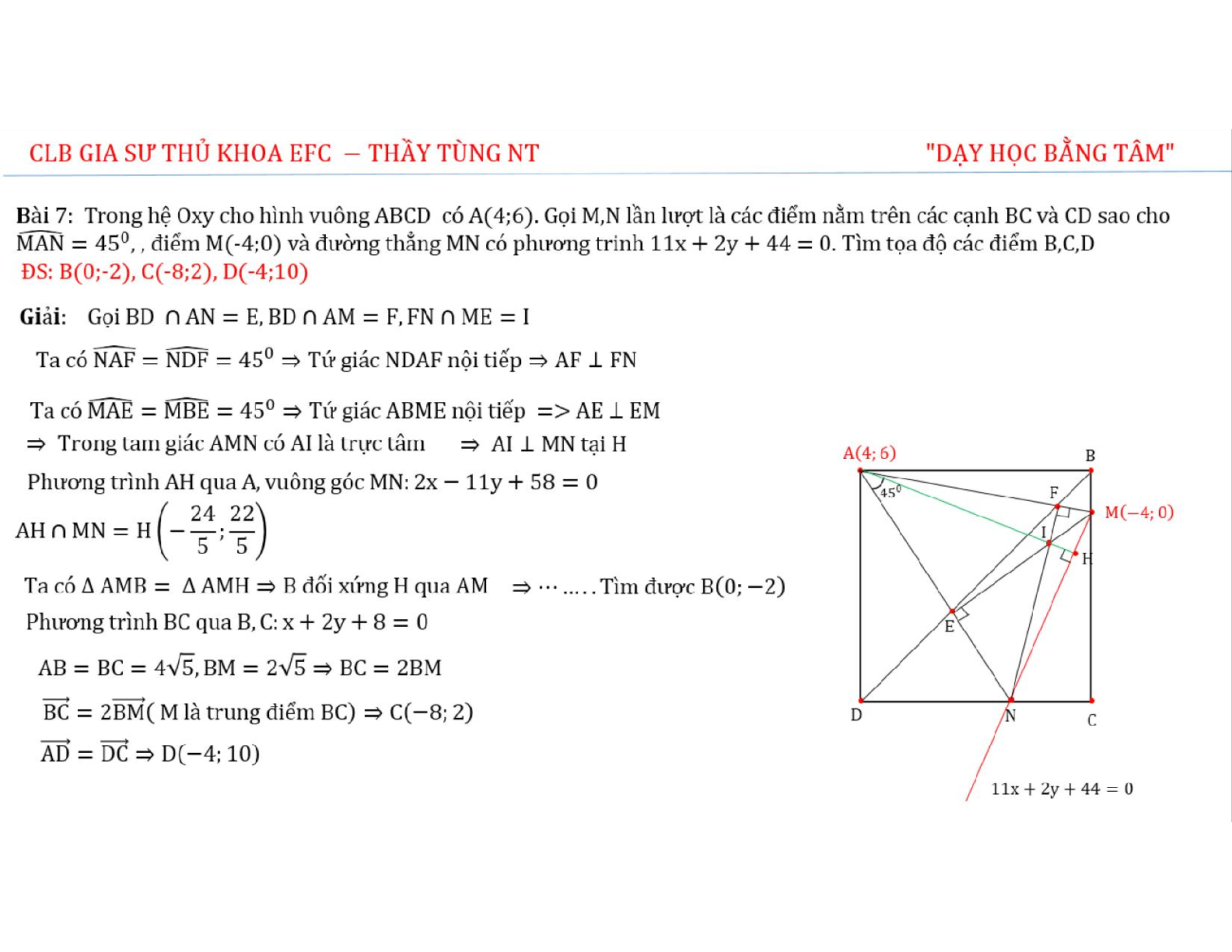
Bài 7: Trong hệ Oxy cho hình vuông ABCD có A(4;6). Gọi M,N lần lượt là các điểm nằm trên các cạnh BC và CD sao cho \(\widehat {MAN} = {45^0}\) , điểm M(-4;0) và đường thẳng MN có phương trinh \(11{\rm{x}} + 2{\rm{y}} + 44 = 0\). Tìm tọa độ các điểm B,C,D.

 ĐS: \({\rm{B}}(0; - 2),{\rm{C}}( - 8;2),{\rm{D}}( - 4;10)\)

Bài 8: Trong hệ Oxy cho hình vuông ABCD có tâm I. Gọi M là điểm đối xứng của D qua . CGọi H,K lần lượt là chân đường cao hạ từ D,C lên AM. Giả sử K(1;1), đỉnh B thuộc đường thẳng: \(5{\rm{x}} + 3{\rm{y}} - 10 = 0\) và phương trình đường thẳng HI: \(3x + y + 1 = 0\). Tìm tọa độ đỉnh B.

ĐS: \(B\left( {\frac{1}{2};\frac{5}{2}} \right)\)

Bài 9: Trong hệ Oxy cho hình vuông ABCD có K là điểm đối xứng với A qua B. Trên cạnh BC, CD lấy các điểm M và N thỏa mãn BM = DN. Phương trình đường thẳng \({\rm{MK}}:{\rm{x}} - {\rm{y}} = 0\), điểm N( -1; -5) . Viết phương trình cạnh AB biết điểm A thuộc trục hoành và điểm M có hoành độ dương.

ĐS: \(x - 2y + 6 = 0\)

Bài 10: Trong hệ Oxy cho hình vuông ABCD có đỉnh C( -4; -3)  và M là một điểm nằm trên cạnh AB(M không trung A,B. Gọi E, F lần lượt là hình chiếu vuông góc của A,C lên DM và \({\rm{I}}(2;3)\) là giao điểm CE và BF. Tìm tọa độ các đỉnh còn lại của hình vuông biết rằng đỉnh B nằm trên đường thẳng d có phương trình \({\rm{x}} - 2{\rm{y}} + 10 = 0\)ĐS:\(A(8;1),B(0;5),D(4; - 7)\)

ĐÁP ÁN CHUYÊN ĐỀ 1

Bài 1: Tương tự Mẫu 1 trong bài giảng video

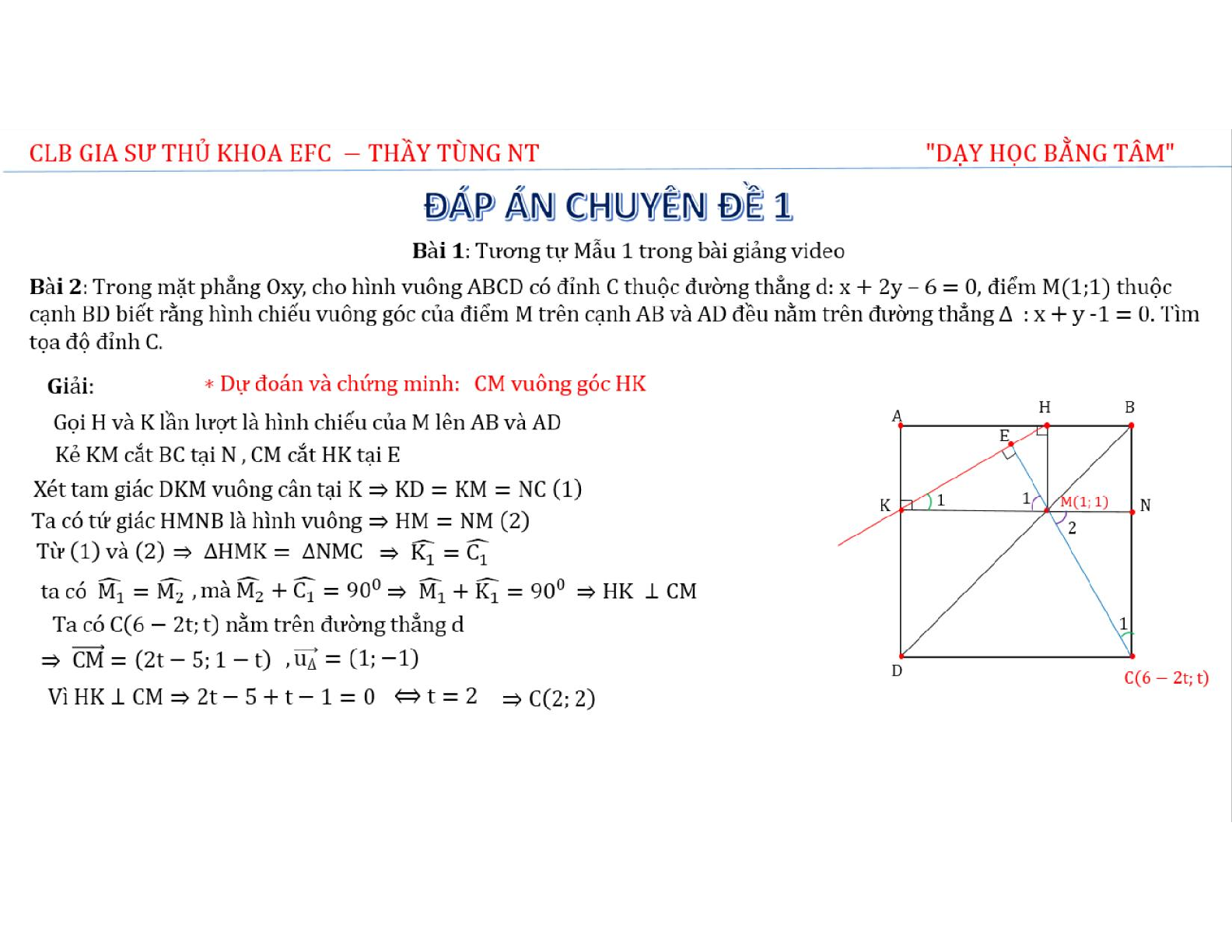
Bài 2: Trong mặt phẳng Oxy, cho hình vuông ABCD có đỉnh C thuộc đường thẳng \({\rm{d}}:{\rm{x}} + 2{\rm{y}} - 6 = 0\), điểm M(1;1) thuộc cạnh BD biết rằng hình chiếu vuông góc của điểm M trên cạnh AB và AD đều nằm trên đường thẳng \(\Delta :{\rm{x}} + {\rm{y}} - 1 = 0\). Tìm tọa độ đỉnh C.

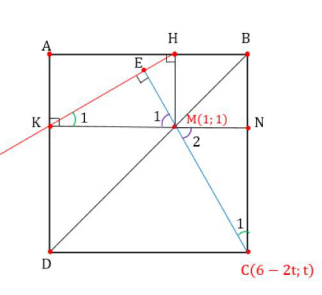
Giải: \(\quad \)

* Dự đoán và chứng minh: CM vuông góc HK

Gọi H và K lần lượt là hình chiếu của M lên AB và AD

Kẻ KM cắt BC tại N, CM cắt HK tại E

Xét tam giác DKM vuông cân tại \({\rm{K}} \Rightarrow {\rm{KD}} = {\rm{KM}} = {\rm{NC}}\) (1)

Ta có tứ giác HMNB là hình vuông \( \Rightarrow {\rm{HM}} = {\rm{NM}}(2)\)

Từ (1) và \((2) \Rightarrow \Delta {\rm{HMK}} = \Delta {\rm{NMC}} \Rightarrow \widehat {{{\rm{K}}_1}} = \widehat {{{\rm{C}}_1}}\)

ta có \(\widehat {{{\rm{M}}_1}} = \widehat {{{\rm{M}}_2}}\), mà \(\widehat {{{\rm{M}}_2}} + \widehat {{{\rm{C}}_1}} = {90^0}\)

\( \Rightarrow \widehat {{{\rm{M}}_1}} + \widehat {{{\rm{K}}_1}} = {90^0} \Rightarrow {\rm{HK}} \bot {\rm{CM}}\)

Ta có \(C(6 - 2t;t)\) nằm trên đường thẳng d

\( \Rightarrow \overrightarrow {{\rm{CM}}}  = (2{\rm{t}} - 5;1 - {\rm{t}}),\overrightarrow {{{\rm{u}}_\Delta }}  = (1; - 1)\)

Vì \({\rm{HK}} \bot {\rm{CM}} \Rightarrow 2{\rm{t}} - 5 + {\rm{t}} - 1 = 0\)

\( \Leftrightarrow {\rm{t}} = 2 \Rightarrow {\rm{C}}(2;2)\)

C\((6 - 2t;t)\)

Bài 3: Trong mặt phẳng Oxy, cho hình vuông ABCD có \(C(2; - 2)\). Gọi I, K lần lượt là trung điểm của DA và DC, M (-1; -1) là giao điểm của BI và AK. Tìm tọa độ các đỉnh còn lại của hình vuông ABCD biết B có hoành độ dương

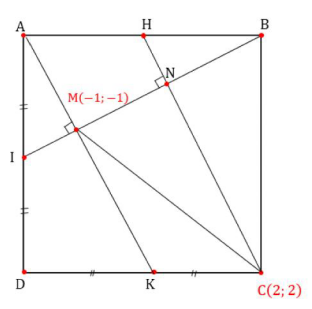
Giải:

\(*\) Chứng minh: \({\rm{AK}} \bot {\rm{IB}}\)

Ta có

\( \Rightarrow \widehat {{\rm{AIB}}} = \widehat {{\rm{AKD}}}\)

mà \(\widehat {{\rm{AKD}}} + \widehat {{\rm{DAK}}} = {90^0}\)

$\Rightarrow \widehat{\text{AIB}}+\widehat{\text{DAK}}={90}^{°}\Rightarrow \text{AK}\perp \text{IB}$

Gọi H là trung điểm AB\( \Rightarrow \) tứ giác AHCK là hình bình hành \( \Rightarrow {\rm{CH}} \bot {\rm{IB}}\) tại N

Xét tam giác ABM có HN là đường trung bình \( \Rightarrow \) N là trung điểm BM

Tam giác BCM có CN vừa là trung tuyến vừa là đường cao

\( \Rightarrow \) Tam giác BCM cân tại \({\rm{C}} \Rightarrow {\rm{BC}} = {\rm{CM}}\)

\(\begin{array}{l} \Rightarrow {\rm{MC}} = {\rm{AB}} = {\rm{BC}} = \sqrt {10} (1)\\\quad {\rm{BI}} = \sqrt {{\rm{A}}{{\rm{B}}^2} + {\rm{A}}{{\rm{I}}^2}}  = \frac{{\sqrt 5 }}{2}\end{array}\)

Ta có \({\rm{A}}{{\rm{B}}^2} = {\rm{BI}}.{\rm{BM}} \Rightarrow {\rm{BM}} = 2\sqrt 2 (2)\)

Điểm B(a,b)

 Từ \((1)\) và \((2) \Rightarrow \left\{ {\begin{array}{*{20}{c}}{{{(a + 1)}^2} + {{(b + 1)}^2} = 8}\\{{{(a - 2)}^2} + {{(b - 2)}^2} = 10}\end{array}\quad  \Rightarrow B(1;1)} \right.\)

Phương trình \({\rm{AB}}:{\rm{x}} - 3{\rm{y}} + 2 = 0\)

\( \Rightarrow A( - 2;0)\)

\(\overrightarrow {{\rm{BA}}}  = \overrightarrow {{\rm{CD}}}  \Rightarrow {\rm{D}}( - 1; - 3)\)

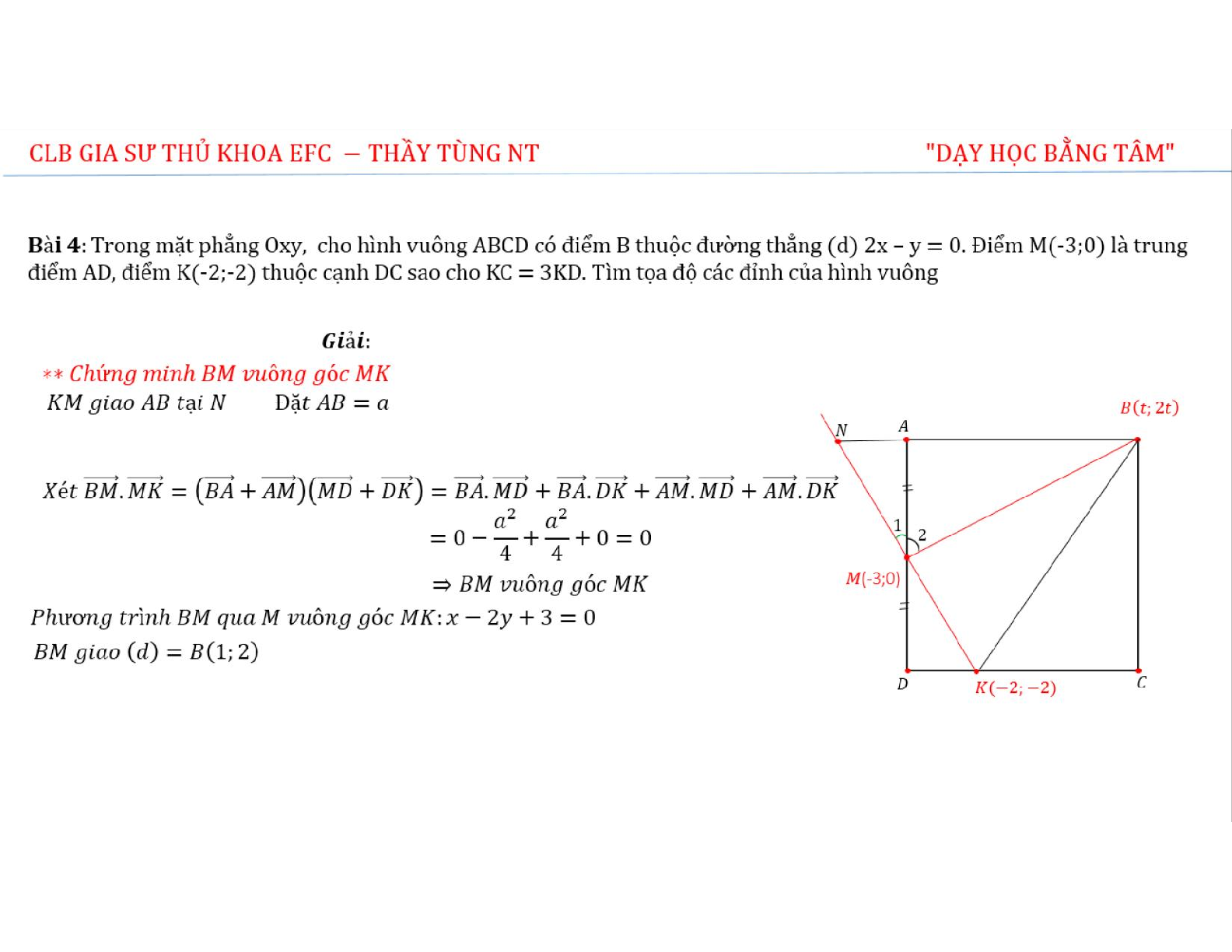
Bài 4: Trong mặt phẳng Oxy, cho hình vuông ABCD có điểm B thuộc đường thẳng \(({\rm{d}})2{\rm{x}} - {\rm{y}} = 0\). Điểm \({\rm{M}}( - 3;0)\) là trung điểm AD, điểm \({\rm{K}}( - 2; - 2)\) thuộc cạnh DC sao cho \({\rm{KC}} = 3{\rm{KD}}\). Tìm tọa độ các đỉnh của hình vuông

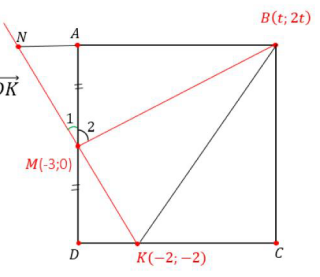
Giải:

** Chứng minh BM vuông góc MK

KM giao AB tại N

Đặt AB = a

Xét \[\overrightarrow {BM}  \cdot \overrightarrow {MK}  = (\overrightarrow {BA}  + \overrightarrow {AM} )(\overrightarrow {MD}  + \overrightarrow {DK} )\]

\[\begin{array}{*{20}{c}}{ = \overrightarrow {BA}  \cdot \overrightarrow {MD}  + \overrightarrow {BA}  \cdot \overrightarrow {DK}  + \overrightarrow {AM}  \cdot \overrightarrow {MD}  + \overrightarrow {AM}  \cdot \overrightarrow {DK} }\\{ = 0 - \frac{{{a^2}}}{4} + \frac{{{a^2}}}{4} + 0 = 0}\end{array}\]

\( \Rightarrow \)BM vuông góc MK

Phương trình BM qua M vuông góc MK: x – 2y + 3 = 0

BM giao (d) = B(1; 2)