Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu Chuyên đề thể tích khối đa diện phần 1, tài liệu bao gồm 30 trang. Tài liệu được tổng hợp từ các tài liệu ôn thi hay nhất  giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kỳ thi sắp hới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây

Tài liệu bao gồm các nội dung sau:

Thể tích vật thể

Thể tích khối chóp

Thể tích khối lăng trụ

Tỉ lệ thể tích

Chuyên đề thể tích khối đa diện phần 1

Vấn đề 1: Thể tích vật thể

0.1 Khái niệm

Thể tích vật thể K là phần mà vật thể đó chiếm chổ trong không gian.

Thể tích của vật thể K được kí hiệu : V

0.2 Tính chất

V là một số lớn hơn 0 thỏa mãn các tính chất sau:

1. Hai khối đa diện bằng nhau thì thể tích bằng nhau.

2. Thể tích khối lập phương bằng 1 thì V = 1.

3. Nếu một khối đa diện được phân chia thành các khối đa diện thì thể tích khối ban đầu bằng tổng thể tích các khối đã phân chia.

0.3 Thể tích khối hộp chữ nhật

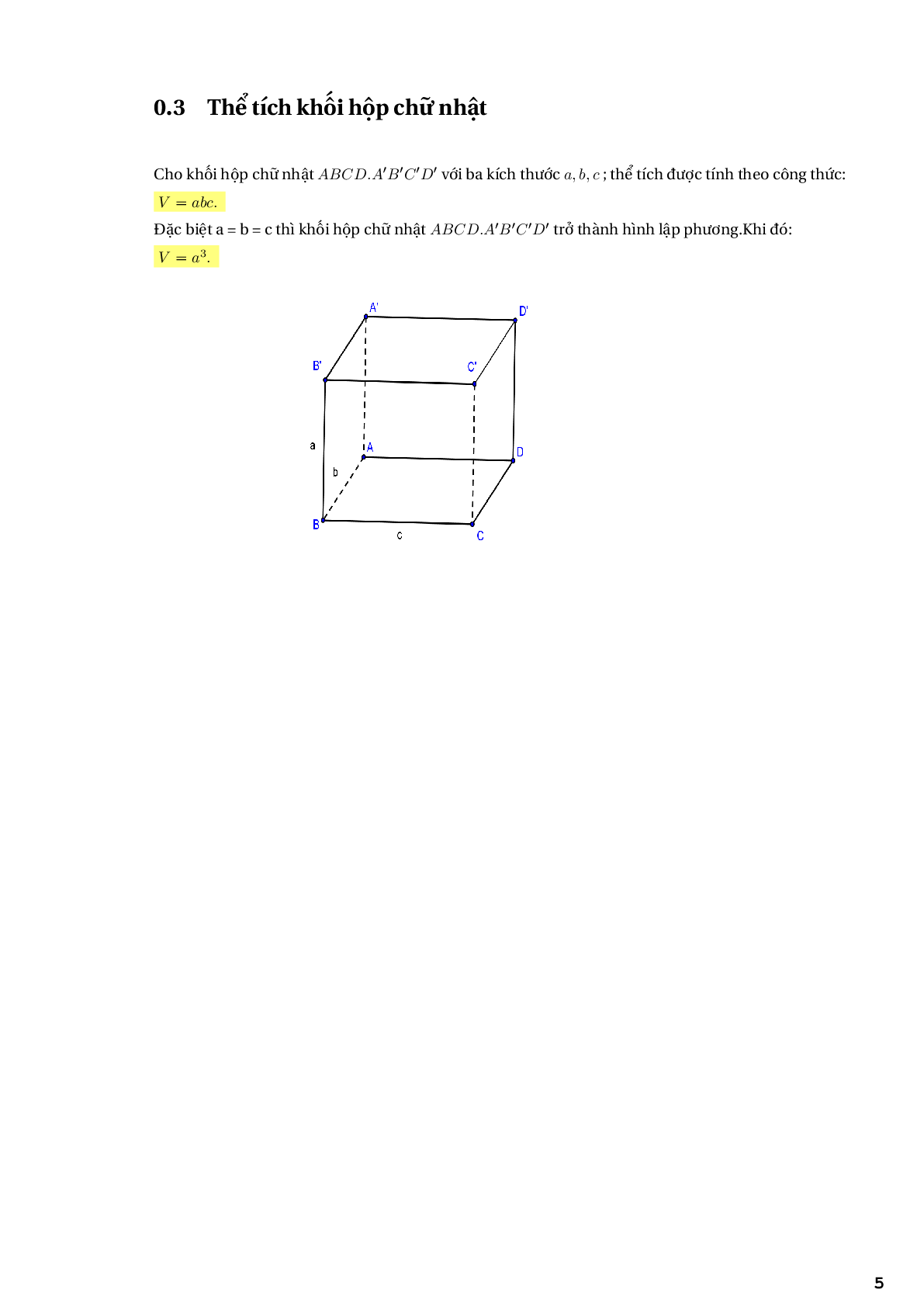
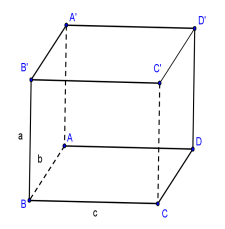
Cho khối hộp chữ nhật \(ABCD \cdot {A^\prime }{B^\prime }{C^\prime }{D^\prime }\) với ba kích thước a, b, c; thể tích được tính theo công thức: V = abc

Đặc biệt a = b = c thì khối hộp chữ nhật \(ABCD \cdot {A^\prime }{B^\prime }{C^\prime }{D^\prime }\) trở thành hình lập phương.Khi đó: \(V = {a^3}\)

vấn đề 2: Thể tích khối chóp

0.4 Công thức tính thể tích khối chóp

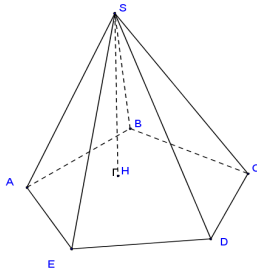
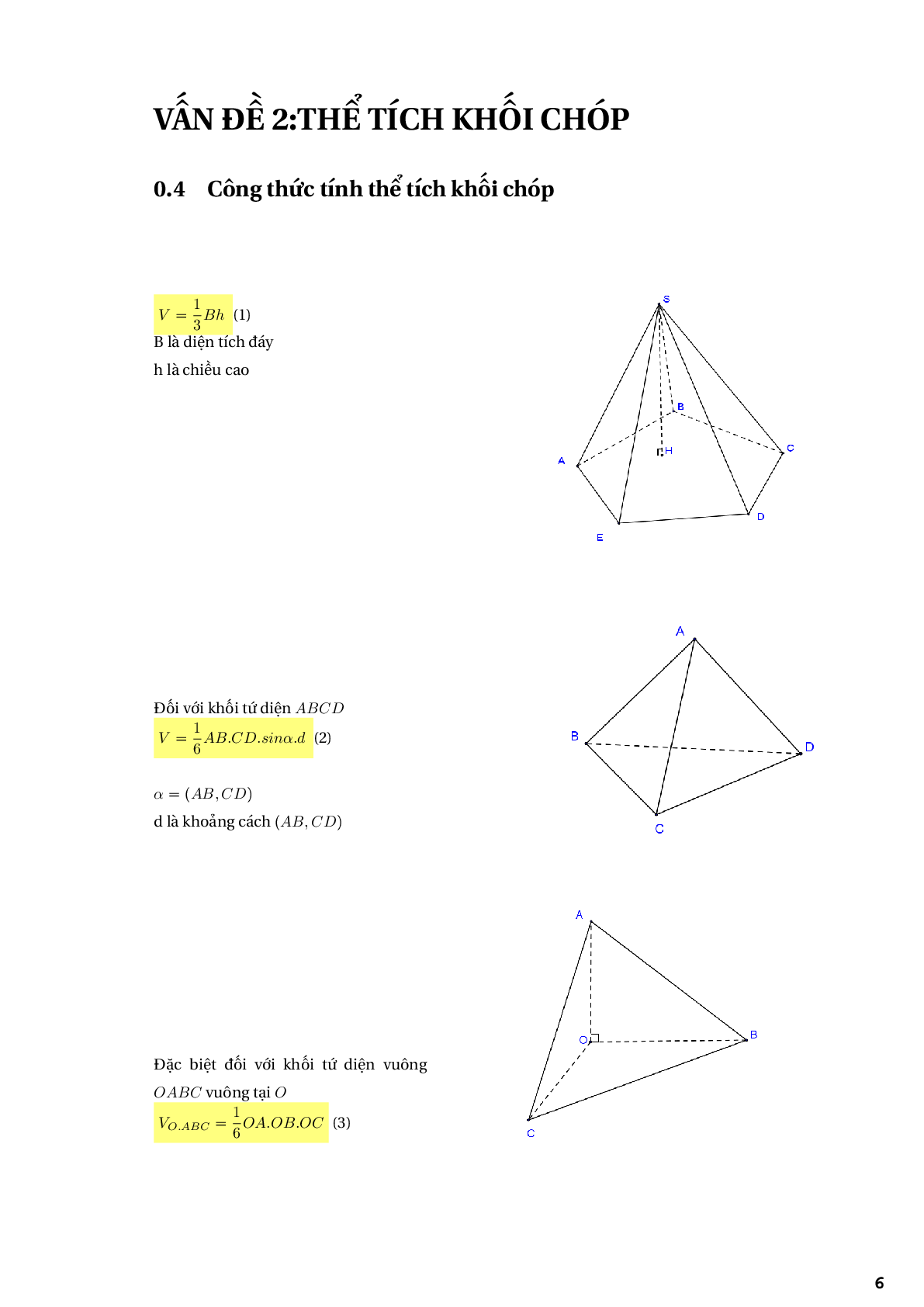
\(V = \frac{1}{3}Bh{\rm{ (1) }}\)

B là diện tích đáy

h là chiều cao

Đối với khối tứ diện ABCD

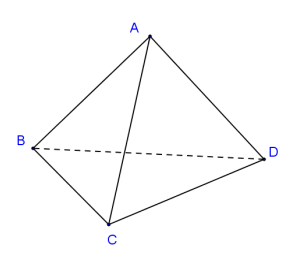
\(V = \frac{1}{6}AB \cdot CD \cdot \sin \alpha .d\)

\(\alpha  = (AB,CD)\)

d là khoảng cách (AB;CD)

Đặc biệt đối với khối tứ diện vuông OABC vuông tại O

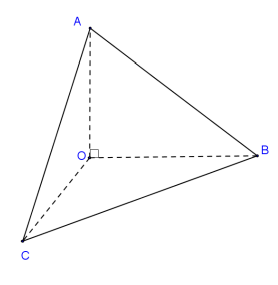
\({V_{O.ABC}} = \frac{1}{6}OA.OB.OC\) (3)

0.5 Phương pháp

Để tính thể tích khối chóp ta cần tính được chiều cao và diện tích đáy

0.5.1 Tính chiều cao

Ta chính xác hóa chân đường cao

1) Hai đường xiên bằng nhau khi và chỉ khi hai hình chiếu bằng nhau, suy ra hình chóp có các cạnh bên bằng nhau thì chân đường cao là tâm đường tròn ngoại tiếp đa giác đáy.

2) Hai mặt phẳng vuông góc với nhau. Đường thẳng nào nằm trong mặt phẳng này mà vuông góc với giao tuyến thì vuông góc với mặt phẳng kia

Suy ra cách tìm hình chiếu H của A trên mp(P)

- Tìm mặt phẳng (Q) chứa A sao cho \((Q) \bot (P)\)

- Xác định giao tuyến d của (P) và (Q)

- Trong (Q) dựng \(AH \bot d\) tại H

3) Hai mặt phẳng cắt nhau cùng vuông góc với một mặt phẳng thì giao tuyến của nó vuông góc với mặt phẳng đó.

4) Hình chóp có các mặt bên tạo với đáy một góc bằng nhau thì chân đường cao trùng với tâm đường tròn nội tiếp đa giác đáy.

0.5.2 Tính diện tích đáy

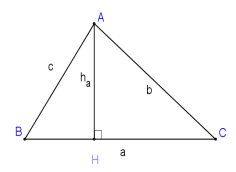
a.Nếu tam giác ABC vuông ở A ta có các hệ thức lượng trong tam giác vuông ABC sau:

\[\begin{array}{l}B{C^2} = A{B^2} + A{C^2}\\BH.BC = A{B^2}\\CH.BC = A{C^2}\\BH.HC = A{H^2}\\AH.BC = AB \cdot AC\\AM = \frac{1}{2}BC\\\sin B = \frac{{AC}}{{BC}} \cdots \\\frac{1}{{A{H^2}}} = \frac{1}{{A{B^2}}} + \frac{1}{{A{C^2}}}\end{array}\]

b.Hệ thức lượng trong tam giác thường

Định lí hàm số cos: \({a^2} = {b^2} + {c^2} - 2bc \cdot \cos A\)

Định lí hàm số sin: \(\frac{a}{{\sin A}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}} = 2R\)

Công thức tính trung tuyến \(A{B^2} + A{C^2} = 2A{M^2} + \frac{{B{C^2}}}{2}\)

c.Một số công thức tính diện tích

Diện tích tam giác

\(\begin{array}{l}S = \frac{1}{2}a \cdot {h_a}\\S = \frac{1}{2} \cdot b \cdot c \cdot \sin A\end{array}\)