Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu Chuyên đề thể tích khối lăng trụ, tài liệu bao gồm 33 trang. Tài liệu được tổng hợp từ các tài liệu ôn thi hay nhất  giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kỳ thi sắp hới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây

2Tài liệu bao gồm các nội dung sau:

Chủ đề 3: Thể tích khối lăng trụ

Dạng 1: Khối lăng trụ đứng

Dạng 2: Khối lăng trụ đều

Dạng 3: Khối lăng trụ xiêng

Chuyên đề thể tích khối lăng trụ

Chủ đề 3. Thể tích khối lăng trụ

1. Định nghĩa: Cho hai mặt song song \((\alpha )\) và \(\left( {{\alpha ^\prime }} \right)\). Trên \((\alpha )\) ta lấy đa giác lôi \({A_1}{A_2} \ldots {A_n}\) ' qua các đỉnh này ta dựng các đường thẳng song song cắt \(\left( \alpha  \right.\) ) tại \({\rm{A}}_1^\prime ,{\rm{A}}_2^\prime , \ldots ,{\rm{A}}_{\rm{n}}^\prime \).

Hình bao gồm hai đa giác \({{\rm{A}}_1}\;{{\rm{A}}_2} \ldots {{\rm{A}}_{\rm{n}}},{\rm{A}}_1^\prime {\rm{A}}_2^\prime  \ldots {\rm{A}}_n^\prime \) và các hình bình hành \({{\rm{A}}_1}\;{{\rm{A}}_2}\;{\rm{A}}_2^\prime {\rm{A}}_1^\prime , \ldots \) Được gọi là hình lăng trụ. Kí hiệu là: \({{\rm{A}}_1}\;{{\rm{A}}_2} \ldots {{\rm{A}}_{\rm{n}}} \cdot {\rm{A}}_1^\prime {\rm{A}}_2^\prime  \ldots {\rm{A}}_{\rm{n}}^\prime \).

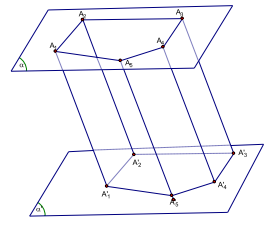
Nhận xét:

- Các mặt bên của hình lăng trụ bằng nhau và song song với nhau

- Các mặt bên là các hình bình hành

- Hai đáy hình lăng trụ là hai đa giác bằng nhau

2. Hình lăng trụ đứng - hình lăng trụ đều, hình hộp chữ nhật và hình lập phương

a) Hình lăng trụ đứng: là hình lăng trụ có cạnh bên vuông góc với đáy. Độ dài cạnh bên được gọi là chiều cao của hình lăng trụ. Lúc đó các mặt bên của hình lăng trụ đứng là các hình chữ nhật

b) Hình lăng trụ đều: là hình lăng trụ đứng có đáy là đa giác đều. Các mặt bên của lăng trụ đều là các hình chữ nhật bằng nhau. Ví dụ: hình lăng trụ tam giác đều, tứ giác đều... thì ta hiểu là hình lăng trụ đều

c) Hình hộp : Là hình lăng trụ có đáy là hình bình hành

d) Hình hộp đứng: là hình lăng trụ đứng có đáy là hình bình hành

e) Hình hộp chữ nhật: là hình hộp đứng có đáy là hình chữ nhật

f) Hình lăng trụ đứng có đáy là hình vuông và các mặt bên đều là hình vuông được gọi là hình lập phương (hay hình chữ nhật có ba kích thước bằng nhau được gọi là hình lập phương)

Nhận xét:

- Hình hộp chữ nhật \( \Rightarrow \) hình lăng trụ đứng (Có tất cả các mặt là hình chữ nhật

- Hình lập phương \( \Rightarrow \) hình lăng trụ đều (tất cả các cạnh bằng nhau)

- Hình hộp đứng \( \Rightarrow \) hình lăng trụ đứng (mặt bên là hình chữ nhật, mặt đáy là hình bình hành)

3. Thể tích khối lăng trụ:

V = B.h: Với B là diện tích đáy và h là chiều cao

4. So sánh khối lăng trụ đứng và khối lăng trụ đều:

Dạng 1. Khối lăng trụ đúng

Câu 1. Cho hình lăng trụ đứng \({\rm{ABC}}\).A'B'C' có thể tích là V. Trong các khối chóp dưới đây, khối chóp có thể tích \(\frac{{2\;{\rm{V}}}}{3}\) là:

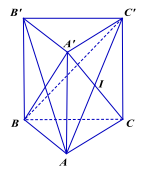
A. A.A' \({{\rm{B}}^\prime }{{\rm{C}}^\prime }\)

B. \({{\rm{C}}^\prime } \cdot {\rm{ABC}}\)

C. \({A^\prime } \cdot BC{C^\prime }{B^\prime }\)

D. I.ABB' \({{\rm{A}}^\prime }\)

Hướng dẫn giải

Ta có: \({{\rm{V}}_{{\rm{ABC}} \cdot {{\rm{A}}^\prime }{{\rm{B}}^\prime }{{\rm{C}}^\prime }}} = {{\rm{V}}_{{{\rm{A}}^\prime } \cdot {\rm{BCC}}{{\rm{B}}^\prime }}}{{\rm{B}}^\prime } + {{\rm{V}}_{{{\rm{A}}^\prime } \cdot {\rm{ABC}}}}\).

Mà \({{\rm{V}}_{{{\rm{A}}^\prime } \cdot {\rm{ABC}}}} = \frac{1}{3}\;{{\rm{V}}_{{\rm{ABC}} \cdot {{\rm{A}}^\prime }{{\rm{B}}^\prime }{{\rm{C}}^\prime }}} \Rightarrow {{\rm{V}}_{{{\rm{A}}^\prime } \cdot {\rm{BCC}}{{\rm{C}}^\prime }}} = \frac{2}{3}\;{{\rm{V}}_{{\rm{ABC}} \cdot {{\rm{A}}^\prime }{{\rm{B}}^\prime }{{\rm{C}}^\prime }}} = \frac{2}{3}\;{\rm{V}}\).

Vậy chọn đáp án C.

Câu 2. Cho hình hộp đứng có các cạnh \({\rm{AB}} = 3{\rm{a}};{\rm{AD}} = 2{\rm{a}};{\rm{A}}{{\rm{A}}^\prime } = 2{\rm{a}}\) như hình vẽ. Thể tích của khối \({D^\prime }\) A'.ACD' là:

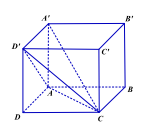
A. \({a^3}\)

B. \(2{a^3}\)

C. \(3{a^3}\)

D. \(6{{\rm{a}}^3}\)

Hướng dẫn giải

Ta có:

\(\begin{array}{l}{{\rm{V}}_{{{\rm{A}}^\prime } \cdot {\rm{ACD}}}}, = \frac{1}{2}\;{{\rm{V}}_{{\rm{C}}.{\rm{AD}}{{{\rm{D'}}}^\prime }}} = \frac{1}{2} \cdot \frac{1}{3} \cdot {{\rm{V}}_{{\rm{ABCD}}{\rm{.A AB'C'}}{{\rm{D}}^\prime }}}\\ = \frac{1}{6} \cdot 3{\rm{a}} \cdot 2{\rm{a}} \cdot 2{\rm{a}} = 2{{\rm{a}}^3}\end{array}\).

Vậy chọn đáp án B.

Câu 3. Cho hình lăng trụ đứng \(ABC.{A^\prime }{B^\prime }{C^\prime }\) có $\text{AC}=\sqrt{3}\text{a},\text{BC}=\text{a},\text{ACB}={150}^{°}$, đường thẳng \({{\rm{B}}^\prime }{\rm{C}}\) tạo với mặt phẳng \(\left( {{\rm{AB}}{{\rm{B}}^\prime }{{\rm{A}}^\prime }} \right)\) một góc \(\alpha \) thỏa mãn \(\sin \alpha  = \frac{1}{4}\). Thể tích khối lăng trụ \(ABC \cdot {A^\prime }{B^\prime }{C^\prime }\) là:

A. \(\frac{{{a^3}\sqrt {105} }}{{28}}\)

B. \(\frac{{{a^3}\sqrt {105} }}{{14}}\)

C. \(\frac{{{a^3}\sqrt {339} }}{{14}}\)

D. \(\frac{{{a^3}\sqrt {339} }}{{28}}\)

Hướng dẫn giải

Ta có

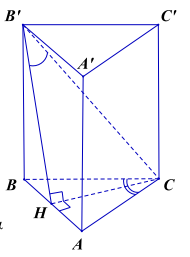
\( = \frac{1}{2}{\rm{a}}\sqrt 3  \cdot {\rm{a}} \cdot \sin {150^0} = \frac{{\sqrt 3 {{\rm{a}}^2}}}{4}\)

Kẻ \({\rm{CH}} \bot {\rm{AB}} \Rightarrow {\rm{CH}} \bot \left( {{\rm{AB}}{{\rm{B}}^\prime }{{\rm{A}}^\prime }} \right)\) nên \({B^\prime }H\) là hình chiếu vuông góc của \({B^\prime }{\rm{C}}\) lên \(\left( {{\rm{ABB}}{{\rm{A}}^\prime }} \right)\) \( \Rightarrow \left( {{{\rm{B}}^\prime }{\rm{C}},\left( {{\rm{ABB}}{{\rm{B}}^\prime }{{\rm{A}}^\prime }} \right)} \right) = \left( {{{\rm{B}}^\prime }{\rm{C}},{{\rm{B}}^\prime }{\rm{H}}} \right) = {\rm{C}}{{\rm{B}}^\prime }{\rm{H}} = \alpha \)

\({\rm{A}}{{\rm{B}}^2} = {\rm{A}}{{\rm{C}}^2} + {\rm{B}}{{\rm{C}}^2} - 2{\rm{AC}} \cdot {\rm{BC}} \cdot \cos {150^0} = 7{{\rm{a}}^2} \Rightarrow {\rm{AB}}\) \({\rm{CH}} = \frac{{2 \cdot {{\rm{S}}_{\Delta {\rm{ABC}}}}}}{{{\rm{AB}}}} = \frac{{{\rm{a}}\sqrt {21} }}{{14}} \Rightarrow {{\rm{B}}^\prime }{\rm{C}} = \frac{{{\rm{CH}}}}{{\sin \alpha }} = \frac{{2{\rm{a}}\sqrt {21} }}{7}\)

Xét \(\Delta {B_B}^\prime {\rm{C}}\) vuông tại \(B\) có:

 \({\rm{B}}{{\rm{B}}^\prime } = \sqrt {{{\rm{B}}^\prime }{{\rm{C}}^2} - {\rm{B}}{{\rm{C}}^2}}  = \frac{{{\rm{a}}\sqrt {35} }}{7}\).

Do đó  Chọn đáp án A

Câu 4. Khối lập phương có độ dài đường chéo bằng d thì thể tích của khối lập phương là:

A. \({\rm{V}} = {{\rm{d}}^3}\)

B. \(\sqrt 3 \;{{\rm{d}}^3}\);

C. \(3\;{{\rm{d}}^3}\);

D. \(V = \frac{{{d^3}\sqrt 3 }}{9}\)

Hướng dẫn giải

Khối lập phương có cạnh là \({\rm{a}} = \frac{{\rm{d}}}{{\sqrt 3 }}\). Do đó khối lập phương có thể tích là \({\rm{V}} = {\left( {\frac{{\rm{d}}}{{\sqrt 3 }}} \right)^3} = \frac{{{{\rm{d}}^3}\sqrt 3 }}{9}\). Vậy chọn đáp án D.

Câu 5. Cho lăng trụ đứng \(ABC.{A^\prime }{B^\prime }{C^\prime }\) có đáy là tam giác cân,\(AB = AC = a,BAC = {120^0}\).Mặt phẳng \(\left( {{\rm{A}}{{\rm{B}}^\prime }{{\rm{C}}^\prime }} \right)\) tạo với mặt đáy góc ${60}^{°}$. Tính thể tích lăng trụ \({\rm{ABC}} \cdot {{\rm{A}}^\prime }{{\rm{B}}^\prime }{{\rm{C}}^\prime }\).

A. \(\frac{8}{3}{a^3}\)

B. \(\frac{3}{8}{a^3}\)

C. \(\frac{{{a^3}}}{8}\);

D. \(\frac{{\sqrt 3 }}{8}{a^3}\)

Hướng dẫn giải

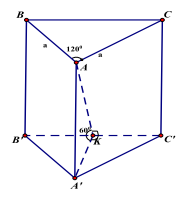
Xác định góc giữa \(\left( {{\rm{A}}{{\rm{B}}^\prime }{{\rm{C}}^\prime }} \right)\) và mặt đáy là ${\text{AKA}}^{\text{'}}\Rightarrow {\text{AKA}}^{\text{'}}={60}^{°}$

Tính

\[\begin{array}{*{20}{c}}{{\rm{A'K}} = \frac{1}{2}{{\rm{A}}^\prime }{\rm{C'}} = \frac{{\rm{a}}}{2}}\\{ \Rightarrow {\rm{A}}{{\rm{A}}^\prime } = {\rm{A'K}} \cdot \tan {{60}^0} = \frac{{{\rm{a}}\sqrt 3 }}{2}}\\{{{\rm{V}}_{{\rm{ABC}} \cdot {\rm{A'B'C'}}}} = {\rm{A}}{{\rm{A}}^\prime } \cdot {{\rm{S}}_{{\rm{ABC}}}} = \frac{{3{{\rm{a}}^3}}}{8}}\end{array}\]

Vậy chọn đáp án B.

Câu 6. Cho lăng trụ đứng \({\rm{ABC}} \cdot {{\rm{A}}^\prime }{{\rm{B}}^\prime }{{\rm{C}}^\prime }\) có đáy ABC là tam giác cân tại A, BC = a, \({\rm{A}}{{\rm{A}}^\prime } = {\rm{a}}\sqrt 2 \) và \(\cos {\rm{BA}}{{\rm{A}}^\prime }{\rm{C}} = \frac{5}{6}\). Tính thể tích hình lăng trụ \({\rm{ABC}} \cdot {{\rm{A}}^\prime }{{\rm{B}}^\prime }{{\rm{C}}^\prime }\).

A. \(\frac{{{a^3}\sqrt 6 }}{4}\)

B. \(\frac{{{a^3}\sqrt 3 }}{4}\)

C. \(\frac{{3{a^3}\sqrt 6 }}{4}\)

D. \(\frac{{3{a^3}\sqrt 3 }}{4}\)

Hướng dẫn giải

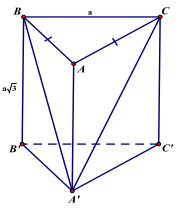
Đặt AB = x thì \({{\rm{A}}^\prime }{{\rm{B}}^2} = {{\rm{A}}^\prime }{{\rm{C}}^2} = {{\rm{x}}^2} + 2{{\rm{a}}^2}\)

Áp dụng định lí hàm số cosin trong  ' \({\rm{BC}}\), ta có:

\(\cos {\rm{B}}{{\rm{A}}^\prime }{\rm{C}} = \frac{{{{\rm{A}}^\prime }{{\rm{B}}^2} + {{\rm{A}}^\prime }{{\rm{C}}^2} - {\rm{B}}{{\rm{C}}^2}}}{{2\;{{\rm{A}}^\prime }{\rm{B}} \cdot {{\rm{A}}^\prime }{\rm{C}}}}\)

\( \Leftrightarrow \frac{{2{{\rm{x}}^2} + 4{{\rm{a}}^2} - {{\rm{a}}^2}}}{{2\left( {{{\rm{x}}^2} + 2{{\rm{a}}^2}} \right)}} = \frac{5}{6} \Leftrightarrow {\rm{x}} = {\rm{a}}\)

Suy ra  đều nên \({{\rm{S}}_{{\rm{ABC}}}} = \frac{{{{\rm{a}}^2}\sqrt 3 }}{4}\)

Vậy thể tích hình lăng trụ \(ABC.{A^\prime }{B^\prime }{C^\prime }\) là \(V = \frac{{{a^3}\sqrt 6 }}{4}\)

Vậy chọn đáp án A.

Câu 7. Cho hình lăng trụ đứng \(ABCD \cdot {A^\prime }{B^\prime }{C^\prime }{D^\prime }\) có đáy ABCD là hình thoi cạnh a, $\text{BAD}={45}^{°},{\text{AA}}^{\text{'}}=\frac{\text{a}\sqrt{2-\sqrt{2}}}{2}$. Thể tích của khối lăng trụ \({\rm{ABCD}} \cdot {{\rm{A}}^\prime }{{\rm{B}}^\prime }{{\rm{C}}^\prime }{{\rm{D}}^\prime }\) là

A. \(\frac{{{a^3}\sqrt {\sqrt 2  - 1} }}{{2\sqrt 2 }}\)

B. \(\frac{{{a^3}\sqrt {\sqrt 2  - 1} }}{{\sqrt 2 }}\)

C. \(\frac{{{a^3}\sqrt {\sqrt 2  - 1} }}{4}\)

D. \(\frac{{{a^3}\sqrt {\sqrt 2  - 1} }}{2}\)

Hướng dẫn giải

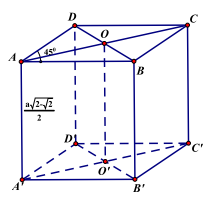
Ta có: \({{\rm{S}}_{{\rm{ABCD}}}} = 2\;{{\rm{S}}_{{\rm{ABD}}}}\)

\({S_{{\rm{ABD}}}} = \frac{1}{2}{\rm{AB}} \cdot {\rm{AD}} \cdot \sin {\rm{BAD}} = \frac{{{{\rm{a}}^2}}}{{2\sqrt 2 }}\)

Do \({\rm{ABCD}} \cdot {{\rm{A}}^\prime }{{\rm{B}}^\prime }{{\rm{C}}^\prime }{{\rm{D}}^\prime }\) là hình đứng nên \({{\rm{V}}_{{\rm{ABCD}} \cdot {{\rm{A}}^\prime }{{\rm{B}}^\prime }{{\rm{C}}^\prime }{{\rm{D}}^\prime }}} = {\rm{A}}{{\rm{A}}^\prime } \cdot {{\rm{S}}_{{\rm{ABCD}}}}\) \( = \frac{{{\rm{a}}\sqrt {2 - \sqrt 2 } }}{2} \cdot \frac{{{{\rm{a}}^2}}}{{\sqrt 2 }} = \frac{{{{\rm{a}}^3}\sqrt {\sqrt 2  - 1} }}{2}\)

Vậy chọn đáp án D.

Câu 8. Cho lăng trụ đứng ABC \({A^\prime }{B^\prime }{C^\prime }\) có đáy ABC là tam giác vuông cân tại B. Biết \({\rm{AB}} = 3\;{\rm{cm}},{\rm{B}}{{\rm{C}}^\prime } = 3\sqrt 2 \;{\rm{cm}}\). Thể tích khối lăng trụ đã cho là

A. \(27\left( {\;{\rm{c}}{{\rm{m}}^3}} \right)\)

B. \(\frac{{27}}{2}\left( {\;{\rm{c}}{{\rm{m}}^3}} \right)\)

C. \(\frac{{27}}{4}\left( {\;{\rm{c}}{{\rm{m}}^3}} \right)\)

D. \(\frac{{27}}{8}\left( {\;{\rm{c}}{{\rm{m}}^3}} \right)\)

Hướng dẫn giải

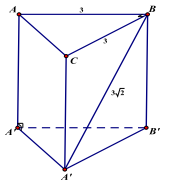
Diện tích đáy của khối lăng trụ  \[{{\rm{S}}_{{\rm{ABC}}}} = \frac{9}{{\rm{a}}}\left( {{\rm{c}}{{\rm{m}}^2}} \right)\]

Chiều cao của khối lăng trụ:

\({\rm{h}} = {\rm{C}}{{\rm{C}}^\prime } = \sqrt {{\rm{B}}{{\rm{C}}^{\prime 2}} - {\rm{B}}{{\rm{C}}^2}}  = 3(\;{\rm{cm}})\)

Thể tích của khối lăng trụ đã cho:

\({\rm{V}} = {{\rm{S}}_{{\rm{ABC}}}} \cdot {\rm{h}} = \frac{9}{2} \cdot 3 = \frac{{27}}{2}\left( {\;{\rm{c}}{{\rm{m}}^3}} \right)\)

Vậy chọn đáp án C.

Câu 9. Cho hình hộp chữ nhật \(ABCD \cdot {A^\prime }{B^\prime }{C^\prime }{D^\prime }\) có \(AB = a,BC = b,A{A^\prime } = c\). Gọi M và N theo thứ tự là trung điểm của \({{\rm{A}}^\prime }{{\rm{B}}^\prime }\) và \({{\rm{B}}^\prime }{{\rm{C}}^\prime }\). Tính tỉ số giữa thể tích khối chóp \({{\rm{D}}^\prime }DMN\) và thể tích khối hộp chữ nhật \({\rm{ABCD}} \cdot {{\rm{A}}^\prime }{{\rm{B}}^\prime }{{\rm{C}}^\prime }{{\rm{D}}^\prime }\)

A. \(\frac{1}{2}\)

B. \(\frac{1}{5}\)

C. \(\frac{1}{8}\)

D. \(\frac{1}{4}\)

Hướng dẫn giải

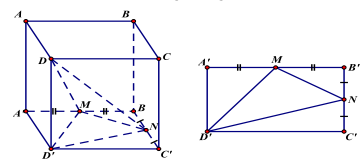
Thể tích khối chóp \({{\rm{D}}^\prime }.{\rm{DMN}}\) bằng thể tích khối chóp D.D'MN

Ta có \({S_{{D^\prime }MN}} = {S_{{A^\prime }{B^\prime }{C^\prime }{D^\prime }}} - \left( {{S_{{D^\prime }{A^\prime }M}} + {S_{{D^\prime }{C^\prime }N}} + {S_{{B^\prime }MN}}} \right)\)

\( = ab - \left( {\frac{{ab}}{4} + \frac{{ab}}{4} + \frac{{ab}}{8}} \right) = \frac{{3ab}}{8}\)

Thể tích khối chóp \({{\rm{D}}^\prime }\).DMN là:

\({{\rm{V}}_1} = \frac{1}{3}\;{{\rm{S}}_{\Delta {D^\prime }{\rm{MN}}}} \cdot {\rm{D}}{{\rm{D}}^\prime } = \frac{1}{3} \cdot \frac{{3{\rm{ab}}}}{8} \cdot {\rm{c}} = \frac{{{\rm{abc}}}}{8}\)

Thể tích của khối hộp chữ nhật \({\rm{ABCD}} \cdot {{\rm{A}}^\prime }{{\rm{B}}^\prime }{{\rm{C}}^\prime }{{\rm{D}}^\prime }\) là

\({\rm{V}} = {\rm{abc}}\) \( \Rightarrow \frac{{{V_1}}}{V} = \frac{1}{8}\). Vậy chọn đáp án C.