Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu Chuyên đề thể tích khối đa diện phần 2, tài liệu bao gồm 19 trang. Tài liệu được tổng hợp từ các tài liệu ôn thi hay nhất  giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kỳ thi sắp hới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây

Chuyên đề thể tích khối đa diện phần 2

Vấn để 1: Ôn tập hình học phẳng

1/ Các hệ thức lượng trong tam giác vuông

Cho  vuông tại A,AH là đường cao, AM là đường trung tuyến. Ta có:

$$\begin{gathered} \begin{array}{l}B{C}^2=A{B}^2+A{C}^2\left(\text{ Pitago }\right)\\ AH.BC=AB.AC\\ A{B}^2=BH.BC,A{C}^2=CH.CB\\ \frac{1}{A{H}^2}=\frac{1}{A{B}^2}+\frac{1}{A{C}^2},A{H}^2=HB.HC\end{array} \\ AM=\frac{BC}{2} \end{gathered}$$

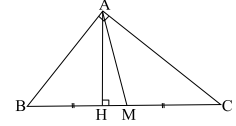
2. Các hệ thức lượng trong tam giác bất kỳ

a. Định lý hàm số cosin

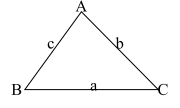
\(\begin{array}{l}{a^2} = {b^2} + {c^2} - 2bc\cos A \Rightarrow \cos A = \frac{{{b^2} + {c^2} - {a^2}}}{{2bc}}\\*{b^2} = {a^2} + {c^2} - 2ac\cos B \Rightarrow \cos B = \frac{{{a^2} + {c^2} - {b^2}}}{{2ac}}\\*{c^2} = {a^2} + {b^2} - 2ab\cos C \Rightarrow \cos C = \frac{{{a^2} + {b^2} - {c^2}}}{{2ab}}\end{array}\)

b. định lý hàm số sin

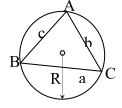
\(\frac{a}{{\sin A}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}} = 2R\)(R là bán kính đường tròn ngoại tiếp  )

c. Công thức tinh diện tích tam giác

 $$\begin{gathered} \diamond S_{△ABC}=\frac{1}{2}a\cdot h_a=\frac{1}{2}b\cdot h_0=\frac{1}{2}c\cdot h_c \\ \diamond S_{△ABC}=\frac{1}{2}ab\sin C=\frac{1}{2}bc\sin A=\frac{1}{2}ac\sin B \\ \diamond S_{△ABC}=\frac{abc}{4R},S_{△ABC}=p\cdot r \\ {S}_{△ABC}=\sqrt{p(p-a)(p-b)(p-c)},\left(p=\frac{a+b+c}{2}\right) \end{gathered}$$

p - nửa chu vi

r - bán kính đường tròn nội tiếp

R - bk đường ngoại nội tiếp

d) Công thức tính độ dài đường trung tuyến của tam giác

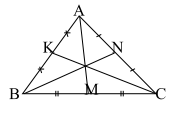
\(\begin{array}{l}*A{M^2} = \frac{{A{B^2} + A{C^2}}}{2} - \frac{{B{C^2}}}{4}\\*B{N^2} = \frac{{B{A^2} + B{C^2}}}{2} - \frac{{A{C^2}}}{4}\\*C{K^2} = \frac{{C{A^2} + C{B^2}}}{2} - \frac{{A{B^2}}}{4}\end{array}\)

3/ Định lí Talet

 $\begin{array}{l}*MN//BC\Rightarrow \frac{AM}{AB}=\frac{AN}{AC}=\frac{MN}{BC}=k\\ *\frac{S_{△AMN}}{S_{△ABC}}={\left(\frac{AM}{AB}\right)}^2=k^2\end{array}$

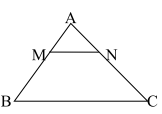
(Tỉ diện tich bằng tỉ bình phương đồng dạng)

4/ Diện tích của đa giác

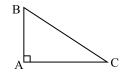
a/ Diện tích tam giác vuông

Diện tích tam giác vuông bẳng \(\frac{1}{2}\) tích 2 cạnh góc vuông.

b) Diện tích tam giác đểu

 $\Rightarrow \left\{\begin{array}{c}{S}_{△ABC}=\frac{a^2\sqrt{3}}{4}\\ h=\frac{a\sqrt{3}}{2}\end{array}\right.$

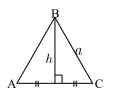
+ Diệ̣n tích tam giác đểu: \(\quad {S_{{\Delta ^{{\rm{d\'e u }}}}}} = \frac{{{{({\rm{ c?nh }})}^2} \cdot \sqrt 3 }}{4}\)

+ Chiểu cao tam giác đều: \({h_\Delta }\) đểu \( = \frac{{({\rm{ c?nh }}) \cdot \sqrt 3 }}{2}\)

c/ Diện tích hình vuông và hình chữ nhật

+ Diện tích hình vuông bẳng cạnh bình phương.

+ Đường chéo hình vuông bằng cạnh nhân \(\sqrt 2 \).

+ Diện tích hình chữ nhật bằng dài nhân rộng.

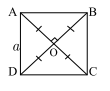
\[ \Rightarrow \left\{ {\begin{array}{*{20}{c}}{{S_{BV}} = {a^2}}\\{AC = BD = a\sqrt 2 }\end{array}} \right.\]

d/ Diện tích hình thang

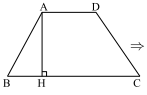
\[S \Rightarrow \frac{{(AD + BC).AH}}{2}\]

Diện tích hình thang

\({{\rm{S}}_{{\rm{Hiah Thang }}}} = \frac{1}{2}\).(đáy lớn + đáy bé). chiều cao

e. Diện tích tứ giác có hai đường chéo vuông góc

+ Diện tích tứ giác có hai đường chéo vuông góc nhau bằng \(\frac{1}{2}\) tích hai đường chéo.

+ Hình thoi có hai đường chéo vuông góc nhau tại trung điềm của mổi đường.

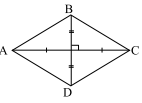
\( \Rightarrow {S_{Hinhthoi}} = \frac{1}{2}AC.BD\)

Lưu ý : Trong tính toán diện tích, ta có thể chia đa giác thành những hình đơn giản để dễ tính diện tích, sau đó cộng các diện tích đục chia này, ta được diện tích đa giác.

Vấn đề 2: Ôn tập hình học không gian 11

1/ Chứng minh đường thẳng \(d//mp(\alpha )\)

a. Phương pháp 1: Chứng minh\[\left\{ {\begin{array}{*{20}{l}}{d//{d^\prime }}\\{{d^\prime } \subset (\alpha )}\\{(d\not  \subset (\alpha ))}\end{array}} \right.\left. {} \right\rangle  \Rightarrow d//mp(\alpha )\]

b. Phương pháp 2: Chứng minh \(\{ \left. {\begin{array}{*{20}{l}}{d \subset (\beta )}\\{(\beta )//(\alpha )}\end{array}} \right\rangle  \Rightarrow d//{\mathop{\rm mp}\nolimits} (\alpha )\)

c. Phương pháp 3: Chứng minh d và \((\alpha )\) cùng vuông góc với một đường thẳng hoặc cùng vuông góc với một mặt phẳng.

2/ Chứng minh \(mp(\alpha )//mp(\beta )\)

a. Phương pháp 1: Chứng minh \(mp(\alpha )\) chứa hai đường thẳng cắt nhau song song với \(mp(\beta )\).

b. Phương pháp 2: Chứng minh \(mp(\alpha )\) và \(mp(\beta )\) cùng song song với 1 mặt phẳng hoặc cùng vuông góc với 1 đường thẳng.

3/ Chứng minh hai đường thẳng song song:

a. Phương pháp 1: Hai \(mp(\alpha ),(\beta )\) có điểm chung S và lần lượt chứa 2 đường thẳng song song a, b thì \((\alpha ) \cap (\beta ) = Sx//a//b\).

b. Phương pháp 2: Chứng minh \(\{ \begin{array}{*{20}{l}}{a//mp(\alpha )}\\{a \subset mp(\beta )}\\{(\alpha ) \cap (\beta ) = b}\end{array}\rangle  \Rightarrow a//b\).

c. Phương pháp 3: Hai mặt phẳng cùng song song với một đường thẳng thì giao tuyến của chúng song song với đường thẳng đó.

d. Phương pháp 4: Một mặt phẳng cắt hai mặt phẳng song song theo giao tuyến song song.

e. Phương pháp 5: Hai đường thẳng cùng vuông góc với một mặt phẳng thì song song với nhau.

f. Phương pháp 6: Sử dụng phương pháp hình học phẳng: Đường trung bình, định lí Talét đảo, ...

4/ Chúrng minh đường thẳng \(d \bot mp(\alpha )\)

a. Phương pháp 1: Chứng minh: \[\left\{ {\begin{array}{*{20}{l}}{d \bot b}\\{a \cap b}\\{a,b \subset mp(\alpha )}\end{array}} \right.\left. {} \right\rangle  \Rightarrow d \bot mp(\alpha )\]

b. Phương pháp 2: Chứng minh: \(\left\{ {\begin{array}{*{20}{l}}{d//{d^\prime }}\\{{d^\prime } \bot mp(\alpha )}\end{array}} \right.\rangle  \Rightarrow d \bot mp(\alpha )\)

c. Phương pháp 3: Chứng minh: \(\left\{ {\begin{array}{*{20}{l}}{d \bot mp(\beta )}\\{mp(\beta )//mp(\alpha )}\end{array} \Rightarrow  \Rightarrow d \bot mp(\alpha )} \right.\)

d. Phương pháp 4: Hai mặt phẳng cắt nhau cùng vuông góc với mặt phẳng thứ 3 thì giao tuyến của chúng vuông góc với mặt phẳng thứ 3:

 \(\left\{ {\begin{array}{*{20}{l}}{(\alpha ) \bot (P)}\\{(\beta ) \bot (P)}\\{(\alpha ) \cap (\beta ) = d}\end{array}} \right\} \Rightarrow d \bot (P)\)

e. Phương pháp 5: Có hai mặt phẳng vuông góc, đường thẳng nào nằm trong mặt phẳng này và vuông góc với giao tuyến của 2 mặt phẳng, cũng vuông góc mặt phẳng  kia: \(\left\{ {\begin{array}{*{20}{l}}{(\alpha ) \bot (\beta )}\\{(\alpha ) \cap (\beta ) = a}\\{d \subset (\alpha )}\\{d \bot a}\end{array}} \right\} \Rightarrow d \bot (\beta )\)

\(5/\) Chứng minh đường thẳng \(d \bot {d^\prime }\)

a. Phưong pháp 1: Đường thẳng \(d \bot (\alpha )\) thì \(d \bot \) tất cả các đường thẳng nằm trong \(mp(\alpha )\).

b. Phương pháp 2: Sử dụng định lý ba đường vuông góc.

c. Phuơng pháp 3: Chứng tỏ góc giữa d và \({d^\prime }\) bằng ${90}^{°}$.

d. Phương pháp 4: Sử dụng hình học phẳng.

6/ Chứng minh \(mp(\alpha ) \bot mp(\beta )\)

a. Phương pháp 1: Chứng minh \(\{ \begin{array}{*{20}{l}}{(\alpha ) \supset d}\\{d \bot (\beta )}\end{array}) \Rightarrow mp(\alpha ) \bot mp(\beta )\) (chứng minh mp chứa 1 đường thẳng vuông góc với mp kia)

b. Phương pháp 2: Chứng tỏ góc giữa hai mặt phẳng bằng ${90}^{°}$.

Phương pháp xác định góc và khoảng cách

(Phần này cần nắm cho thật vững)

I. Tính góc

1. Tính góc giữa hai đường thẳng a và b chéo nhau

Phương pháp : Có thể sử dụng một trong các cách sau:

a. Cách 1: (theo phương pháp hình học)

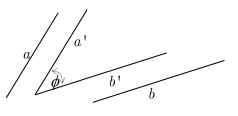
+ Góc giữa hai đường thẳng song song hoặc trùng nhau thì bằng 0

+ Góc giữa hai đường thẳng chéo nhau: Là góc tạo bởi hai đường thẳng cắt nhau lần lượt về cùng phương với hai đường thẳng đó:

\[\left\{ {\begin{array}{*{20}{l}}{a//a'}\\{b//b'}\end{array}} \right. \Rightarrow (\widehat {a,b}) = \left( {\widehat {a',b'}} \right) = \phi \]

(chú ý: Góc giũa hai đường thẳng chỉ lấy góc nhọn không lấy góc tù)

Cách 2: ( theo phương pháp vecto ): \[\cos (a,b) = \frac{{|\vec a \cdot \vec b|}}{{|\vec a| \cdot |\vec b|}}\]

2. Tính góc giữa đường thẳng a và mặt phẳng (P)

Phương pháp xác định:

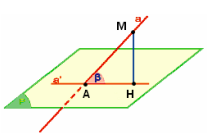
\[ + a \cap (P) = \{ A\} \]

+ Trên đường thẳng a lấy điểm M bất kỳ

+ Tìm điểm H là hình chiếu của M lên mp(P) \( \Rightarrow MH \bot (P)\)

+ \(\widehat {a;(P)} = \widehat {MAH} = \beta \)

 Chú ý: đường thẳng song song hoặc trùng với mặt phẳng thì góc bằng 0.

3. Xác định góc giữa hai mặt phẳng (P) và (Q)

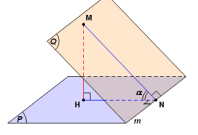
Phương pháp :

+ Tìm giao tuyến của mặt phẳng (P) và (Q)

+ Tìm đường thẳng nằm trong 2 mặt phẳng (P) và (Q) đồng thời 2 đường thẳng này cùng vuông góc với giao tuyến chung của 2 mặt phẳng  (P) và (Q).

+ Góc của 2 mặt phẳng (P) và (Q) là góc của 2 đường thẳng cùng vuông góc với giao tuyến chung của 2 mặt phẳng (P) và (Q)

Chú ý: 2 mặt phẳng song song hoặc trùng nhau thì góc bằng 0

II. Tính khoảng cách

1. Tính các khoảng cách giữa một diểm và mặt phẳng

Phương pháp : Để tính khoảng cách từ một điểm đến một mặt phẳng, ta phải đi tìm đoạn vuông góc vẽ từ điểm đó đến mặt phẳng, ta hay dùng một trong hai cách sau :

Cách 1 :

+ Tìm một mặt phẳng (Q) chứa M và vuông góc với (P).

+ Xác định \(m = (P) \cap (Q)\).

+ Dựng\(MH \bot m = (P) \cap (Q), \Rightarrow MH \bot (P)\)

Cách 2: Dựng \(MH//AK \bot (P)\)

Chú ý :

+ Nếu \(MA//(P) \Rightarrow {d_{[M,(P)]}} = {d_{[M,(P)]}}\)

+ Nếu \(MA \cap (P) = I \Rightarrow \frac{{d[M,(P)]}}{{d[M,(P)]}} = \frac{{IM}}{{IA}}\)

2. Khoảng cách từ một đường thẳng đến một mặt phẳng:

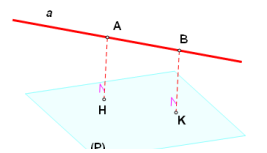
+ Khi \(a//(P) \Rightarrow d[a,(P)] = d[A,(P)]\) với \(A \in (P)\).

+ Khi đường thẳng \[a \cap \left( P \right)\] hoặc \(a \subset (P)\) thì khoàng cách bằng 0

3. Khoảng cách từ một mặt phẳng đến một mặt phẳng.

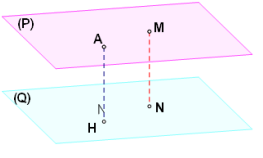
+ Khi \((P)//(Q) \Rightarrow {d_{[(P),(Q)]}} = {d_{[M,(Q)]}}\)với \(A \in (P)\).

+ Khi \(\left[ {\begin{array}{*{20}{c}}{(P) \cap (Q)}\\{(P) \equiv (Q)}\end{array} \Rightarrow {d_{[(P),(Q)]}} = 0} \right.\)

4. Khoảng cách giũa hai đường thẳng

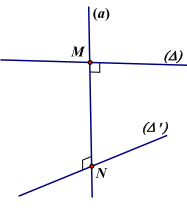
a) Khi \(\left[ {\begin{array}{*{20}{l}}{(\Delta ) \cap \left( {{\Delta ^\prime }} \right)}\\{(\Delta ) \equiv \left( {{\Delta ^\prime }} \right)}\end{array} \Rightarrow {d_{\left[ {(\Delta ),\left( {{\Delta ^\prime }} \right)} \right]}} = 0} \right.\).

b) Khi \((\Delta )//\left( {{\Delta ^\prime }} \right) \Rightarrow {d_{\left[ {(\Delta ),\left( {{\Delta ^\prime }} \right)} \right]}} = {d_{\left[ {M,\left( {{\Delta ^\prime }} \right)} \right]}} = {d_{[N,(\Delta )]}}\) với \(M \in (\Delta ),N \in \left( {{\Delta ^\prime }} \right)\)

c. Khi hai đường chéo nhau:

+ Đường vuông góc chung của hai đường thẳng chéo nhau \((\Delta )\) và \(\left( {{\Delta ^\prime }} \right)\) là đường thẳng \((a)\) cắt \((\Delta )\) ở M và cắt \(\left( {{\Delta ^\prime }} \right)\) ở N đồng thời vuông góc với cả \((\Delta )\) và \(\left( {{\Delta ^\prime }} \right)\).

+ Đoạn MN được gọi là đoạn vuông góc chung của hai đường thẳng chéo nhau \((\Delta )\) và \(\left( {{\Delta ^\prime }} \right)\).

+ Khoảng cách giữa hai đường thẳng chéo nhau là độ dài đoạn vuông góc chung của hai đường thẳng đó .

Phương pháp :

+ Cách 1 : Dựng mặt phẳng (P) chứa đường thẳng a và song song với b.Tính khoảng cách từ b đến mp(P)

+ Cách 2 : Dựng hai mặt phẳng song song và lần lượt chứa hai đường thẳng . Khoảng cách giữa hai mặt phẳng đó là khoảng cách cần tìm .

+ Cách 3 : Dựng đoạn vuông góc chung và tính độ dài đoạn đó .

* Cách dựng đoạn vuông góc chung của hai đường thẳng chéo nhau :

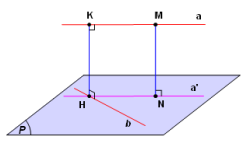
+ Dựng \((P) \supset b,(P)//a\).

+ Dựng \({a^\prime } = hch{(P)^a}\), bằng cách lấy \(M \in a\)

+ Dựng đoạn \(MN \bot (\alpha )\), lúc đó \(a\) ' là đường thẳng đi qua N và song song a.

+ Gọi \(H = {a^\prime } \cap b\), dựng \(HK//MN\)

=> HK là đoạn vuông góc chung cần tìm

( Hay MN là đợn vuông góc chung cần tìm).

* Nếu hai đường thẳng chéo nhau và vuông góc với nhau thì:

+ Dựng một \(mp(P) \supset b,(P) \bot a\) tại H.

+ Trong \((P)\) dựng \(HK \bot b\) tại K.

+ Đoạn HK là đoạn vuông góc chung của a và b.