Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu Các dạng toán đường thẳng và mặt phẳng trong không gian quan hệ song song, tài liệu bao gồm 138 trang. Tài liệu được tổng hợp từ các tài liệu ôn thi hay nhất  giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kỳ thi sắp hới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây

Tài liệu bao gồm các nội dung sau:

Dạng 1. Lý thuyết

Dạng 2. Xác định giao tuyến của 2 mặt phẳng.

Dạng 3. Tìm giao điểm

Dạng 4. Tìm thiết diện

Dạng 5. Đồng quy, thẳng hàng.

Dạng 6. Tỉ số

Các dạng toán đường thẳng và mặt phẳng trong không gian quan hệ song song

Đường thẳng và mặt phẳng

Phần A. Câu hỏi

Dạng 1. Lý thuyét

Câu 1. Trong các khẳng định sau, khẳng định nào đúng?

A. Nếu hai mặt phẳng phân biệt lần lượt chứa hai đường thẳng song song thì giao tuyến của chúng (nếu có) cũng song song với hai đường thẳng đó hoặc trùng với một trong hai đường thẳng đó.

B. Nếu ba mặt phẳng đôi một cắt nhau theo ba giao tuyến thì ba giao tuyến đấy hoặc đồng qui hoặc đôi một song song.

C. Nếu hai mặt phẳng phân biệt lần lượt chứa hai đường thẳng song song thì giao tuyến của chúng (nếu có) cũng song song với hai đường thẳng đó.

D. Hai mặt phẳng cùng song song với đường thẳng thứ ba thì song song với nhau.

Câu 2. Một mặt phẳng hoàn toàn được xác định nếu biết điều nào sau đây?

A. Một đường thẳng và một điểm thuộc nó. \(\quad \)

B. Ba điểm mà nó đi qua.

C. Ba điểm không thẳng hàng.

D. Hai đường thẳng thuộc mặt phẳng.

Câu 3. Trong các tính chất sau, tính chất nào không đúng?

A. Có hai đường thẳng phân biệt cùng đi qua hai điểm phân biệt cho trước.

B. Tồn tại 4 điểm không cùng thuộc một mặt phẳng.

C. Có một và chỉ một mặt phẳng đi qua ba điểm không thẳng hàng.

D. Nếu một đường thẳng đi qua hai điểm thuộc một mặt phẳng thì mọi điểm của đường thẳng đều thuộc mặt phẳng đó.

Câu 4. (HKI-Chuyên Hà Nội - Amsterdam 2017-2018) Chọn mệnh đề đúng trong các mệnh đề sau:

A. Ba đường thẳng đôi một song song thì chúng cùng nằm trên một mặt phẳng.

B. Ba đường thẳng phân biệt đôi một cắt nhau thì chúng cùng nằm trên một mặt phẳng.

C. Ba đường thẳng đôi một cắt nhau thì chúng đồng quy tại một điểm.

D. Cả A, B, C đều sai.

Câu 5. Cho các khẳng định:

(1): Hai mặt phẳng có một điểm chung thì chúng có một đường thẳng chung duy nhất.

(2): Hai mặt phẳng phân biệt có một điểm chung thì chúng có một đường thẳng chung duy nhất.

(3): Hai mặt phẳng có một điểm chung thì chúng còn có vô số điểm chung khác nữa.

(4): Nếu ba điểm phân biệt cùng thuộc hai mặt phẳng thì chúng thẳng hàng.

Số khẳng định sai trong các khẳng định trên là

A. 1 .

B. 2 .

C. 3 .

D. 4 .

Câu 6. Trong các mệnh đề sau, mệnh đề nào đúng?

A. Hai đường thẳng phân biệt không song song thì cheo nhau.

B. Hai đường thẳng không có điểm chung thì chéo nhau.

C. Hai đường thẳng chéo nhau thì không có điểm chung.

D. Hai đường thẳng lần lượt nằm trên hai mặt phẳng phân biệt thì chéo nhau.

Câu 7. Cho hai đường thẳng a và b chéo nhau. Có bao nhiêu mặt phẳng chứa a và song song với b

A. 0 .

B. Vô số.

C. 2 .

D. 1

Câu 8. Trong các hình vẽ sau hình nào có thể là hình biểu diễn của 1 hình tứ diện? ( chọn câu đúng và đầy đủ nhất)

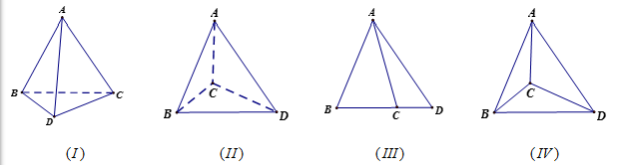
A. (I);(II).

B.(I),(I I),(I I I),(I V).

C. (I).

D. (i);(II);(III).

Câu 9. (Chuyên Nguyễn Huệ - Hà Nội -HK1 2018 - 2019) Một hình chóp có đáy là ngũ giác có số cạnh là

A. 9 cạnh.

B. 10 cạnh.

C. 6 cạnh.

D. 5 cạnh.

Câu 10. (HKI – TRIỆUU QUANG PHỤC 2018-2019) Một hình chóp có đáy là ngũ giác có số mặt và số cạnh là

A. 5 mặt, 5 cạnh.

B. 6 mặt, 5 cạnh.

C. 6 mặt, 10 cạnh.

D. 5 mặt, 10 cạnh.

Câu 11. (Lương Thế Vinh - Kiểm tra giữa HK1 lớp 11 năm 2018 - 2019) Hình chóp có 16 cạnh thì có bao nhiêu mặt?

A. 10 .

B. 8 .

C. 7 .

D. 9 .

Câu 12. Cho hình chóp S,ABC. Gọi M, N, K, E lần lượt là trung điểm của SA, SB, SC, BC. Bốn điểm nào sau đây đồng phẳng?

A. M, K, A, C.

B. M, N, A, C.

C. M, N, K, C.

D. M, N, K, E.

Câu 13. (THPT KINH MÔN - HD - LẦN 2 - 2018) Chọn mệnh đề đúng trong các mệnh đề sau đây:

A. Trong không gian hai đường thẳng chéo nhau thì không có điểm chung.

B. Trong không gian hai đường thẳng phân biệt cùng song song với một mặt phẳng thì song song với nhau.

C. Nếu mặt phẳng (P) chứa hai đường thẳng cùng song song với mặt phẳng (Q) thì (P) và (Q) song song với nhau.

D. Trong không gian hình biểu diễn của một góc thì phải là một góc bằng nó.

Câu 14. (THPT CHUYÊN VĨNH PHÚC - LẦN 3 - 2018) Trong không gian cho bốn điểm không đồng phẳng, có thể xác định nhiều nhất bao nhiêu mặt phẳng phân biệt từ các điểm đó?

A. 3 .

B. 4 .

C. 2 .

D. 6 .

Câu 15. (THPT NGUYỄN HUỆ - NINH BINH - 2018) Cho tam giác ABC khi đó số mặt phẳng qua A và cách đều hai điểm B và C là?

A. 0 .

B. 1 .

C. 2 .

D. Vô số.

Câu 16. Cho mặt phẳng (P) và hai đường thẳng song song a và b. Mệnh đề nào sau đây đúng?

A. Nếu (P) song song với a thì (P) cũng song song với b.

B. Nếu (P) cắt  a thì (P) cũng cắt b.

C. Nếu (P) chứa a thì (P) cũng chứa b.

D. Tất cả các khẳng định trên đều sai.

Dạng 2. Xác định giao tuyến của 2 mặt phẳng

Câu 17. Cho hình chóp S.ABCD với ABCD là hình bình hành. Khi đó giao tuyến của hai mặt phẳng (SAC) và (SAD) là

A. Đường thẳng SC.

B. Đường thẳng SB.

C. Đường thẳng SD

D. Đường thẳng SA

Câu 18. Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi M, N lần lượt là trung điểm của  AD và BC. Giao tuyến của (SMN) và (SAC) là

A. SK ( K là trung điểm của AB).

B. SO (O là tâm của hình bình hành A B C D)

C. SF\((\)F là trung điểm của CD).

D. S D

Câu 19; Cho hình chóp S.ABCD có đáy ABCD là hình thang với đáy lớn \(AD,AD = 2BC\). Gọi O là giao điểm của AC và BD. Tìm giao tuyến của hai mặt phẳng (SAC) và (SBD).

A. SA.

B. AC.

C. SO.

D. SD

Câu 20: Cho hình chóp S.ABCD. Giao tuyến của hai mặt phẳng (SAB) và (SBC) là

A. SA.

B. SB.

C. SC.

D. AC

Câu 21. Cho hình chóp S.ABCD có đáy là hình thang \(ABCD(AD//BC)\). Gọi M là trung điểm của CD. Giao tuyến của hai mặt phẳng (MSB) và (SAC) là:

A. SP với P là giao điểm của AB và CD.

B. SI với I là giao điểm của AC và BM.

C. SO với O là giao điểm của AC và BD.

D. SJ với J là giao điểm của AM và BD

Câu 22. Cho hình chóp S.ABCD, biết AC cắt BD tại M, AB cắt CD tại O. Tìm giao tuyến của hai mặt phẳng (SAB) và (SCD).

A. SO.

B. SM.

C. SA.

D. SC.

Câu 23. Cho hình chóp S.ABCD có đáy ABCD là hình thang, đáy lớn là AB. Kết luận nào sau đây sai?

A. Giao tuyến của hai mặt phẳng (SAD) và (SBC) là đường thẳng đi qua S và không song song với AD.

B. Giao tuyến của hai mặt phẳng (SAD) và (SBC)  là đường thẳng đi qua S và song song với AD

C. Giao tuyến của hai mặt phẳng (SAB) và (SCD) là đường thẳng đi qua  S và song song với CD

D. Giao tuyến của hai mặt phẳng (SAC) và (SBD) là đường thẳng đi qua S và giao điểm của AC  và DB.

Câu 24. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi I và J lần lượt là trung điểm của SA và SB. Khẳng định nào sau đây sai?

A. \((SAB) \cap (IBC) = IB\).

B. IJCD là hình thang.

C. \((SBD) \cap (JCD) = JD\).

D. \((IAC) \cap (JBD) = AO(O\) là tâm ABCD).

Câu 25. Cho hình chóp S.ABCD có \(AC \cap BD = M,AB \cap CD = N\). Giao tuyến của hai mặt phẳng (SAB) và (SCD) là:

A. SM.

B. SA.

C. MN.

D. SN

Câu 26. Cho hình chóp  S.ABCD có đáy là hình thang ABCD \((AD//BC)\). Gọi M là trung điểm CD. Giao tuyến của hai mặt phẳng (MSB) và (SAC) là

A. SI\((\)I là giao điểm của AC và BM)

B. SO (0 là giao điểm của AC và BD).

C. SJ\((\)J là giao điểm của AM và BD)

D. SP(P là giao điểm của AB và CD).

Câu 27. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O, M là trung điểm SC. Khẳng định nào sau đây sai?

A. Giao tuyến của (SAC) và (ABCD) là AC.

B. SA và BD chéo nhau.

C. AM cắt (SBD).

D. Giao tuyến của (SAB) và (SCD) là SO

Câu 28. Cho tứ diện ABCD, M là trung điểm của AB, N là điểm trên AC mà \(AN = \frac{1}{4}AC,P\) là điểm trên đoạn AD mà \(AP = \frac{2}{3}AD\). Gọi E là giao điểm của MP và B D, F là giao điểm của MN và BC. Khi đó giao tuyến của (BCD) và (CNP) là

A. CP.

B. NE.

C. M F.

D. C E.

Câu 29. Cho bốn điểm A, B, C, D không đồng phẳng. Gọi I, K lần lượt là trung điểm hai đoạn thẳng AD và BC. IK là giao tuyến của cặp mặt phẳng nào sau đây ?

A. \((IBC)\) và \((KBD)\).

B. \((IBC)\) và \((KCD)\).

C. \((IBC)\) và \((KAD)\).

D. \((ABI)\) và \((KAD)\).

Câu 30. (THPT TỨ KỲ - HẢI DƯƠNG - LẦN 2 - 2018) Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm AD và AC. Gọi G là trọng tâm tam giác BCD. Giao tuyến của hai mặt phẳng (GMN) và (BCD) là đường thẳng:

A. qua M và song song với AB.

B. Qua N và song song với BD.

C. qua G và song song với CD.

D. qua G và song song với BC.

Dạng 3. Tìm giao điểm

Câu 31. Cho hình chóp S.ABCD có I là trung điểm của SC, giao điểm của AI và (SBD) là

A. Điểm K (với O là trung điểm của BD và \(K = SO \cap AI\) ).

B. Điểm M (với O là giao điểm của AC và BD, M là giao điểmS O và A I)

C. Điểm N ( với O là giao điểm của AC và BD, N là trung điểm của SO)

D. Điểm I.

Câu 32. Cho hình chóp S.ABCD có đáy là hình bình hành. M, N lần lượt thuộc đoạn  SB, SC. Khẳng đinh nào sau đây đúng?

A. Giao điểm của MN và (SBD) là giao điểm của MN và SB.

B. Đường thẳng MN không cắt mặt phẳng (SBD).

C. Giao điểm của MN và (SBD) là giao điểm của MN và SI, trong đó I là giao điểm của CM vả BD.

Câu 33. Cho tứ giác ABCD có AC và BD giao nhau tại O và một điểm S không thuộc mặt phẳng (ABCD). Trên đoạn SC lấy một điểm M không trùng với S và C. Giao điểm của đường thẳng SD với mặt phẳng (ABM) là

A. giao điểm của SD và BK ( với \(K = SO \cap AM\))

B. SD và AM.

C. giao điểm của SD và AB.

D. giao điểm của SD và MK ( với \(K = SO \cap AM\)).

Câu 34. Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm các cạnh AD, BC ; G là trọng tâm của tam giác BCD. Khi đó, giao điểm của đường thẳng MG và mặt phẳng (ABC) là:

A. Điểm A.

B. Giao điểm của đường thẳng MG và đường thẳng AN.

C. Điểm N.

D. Giao điểm của đường thẳng MG và đường thẳng C.

Câu 35. Cho hình chóp S . A B C D có đáy là hình bình hành. M là trung điểm của SC. Gọi I là giao điểm của đường thẳng AM với mặt phẳng (SBD). Chọn khẳng định đúng trong các khẳng định sau đây:

A. \(IA = 3IM\).

B. \(IM = 3IA\).

C. \(IM = 2IA\).

D. \(IA = 2IM\).

Câu 36. (HKI-Chuyên Hà Nội - Amsterdam 2017-2018) Cho tứ diện ABCD có M, N theo thứ tự là trung điểm của AB, BC. Gọi P là điểm thuộc cạnh CD sao cho \(CP = 2PD\) và Q là điểm thuộc cạnh AD sao cho bốn điểm M, N, P, Q đồng phẳng. Khẳng định nào sau đây đúng?

A. Q là trung điểm của đoạn thẳng AC.

B. \(DQ = 2AQ\)

C. \(AQ = 2DQ\)

D. \(AQ = 3DQ\).

Câu 37. (THI HK1 LỚP 11 THPT VIỆT TRÌ 2018 - 2019) Cho tứ diện ABCD, gọi E, F lần lượt là trung điểm của AB, CD ; G là trọng tâm tam giác BCD. Giao điểm của đường thẳng EG và mặt phẳng ACD là

A. Giao điểm của đường thẳng EG và  AF.

B. Điểm F.

C. Giao điểm của đường thẳng EG và CD.

D. Giao điểm của đường thẳng EG và AC

Câu 38. Cho tứ diện ABCD có M, N lần lượt là trung điểm của BC, AD. Gọi G là trọng tâm của tam giác BCD. Gọi I là giao điểm của NG với mặt phẳng (ABC). Khẳng định nào sau đây đúng?

A. \(I \in AM\)

B. \(I \in BC\)

C. \(I \in AC\).

D. \(I \in AB\)

 

 

Xem thêm