Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu Phân chia, lắp ghép khối đa diện Toán lớp 12, tài liệu bao gồm 3 trang có phương pháp giải chi tiết và bài tập, giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kì thi THPT môn Toán sắp tới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Tài liệu Bài tập Phân chia, lắp ghép khối đa diện gồm các nội dung chính sau:

A. Phương phương giải

- Gồm phương pháp giải Bài tập Phân chia, lắp ghép khối đa diện.

B. Bài tập tự luyện

- Gồm 8 bài tập tự luyện có đáp án và lời giải chi tiết giúp học sinh tự rèn luyện cách giải các dạng Bài tập Phân chia, lắp ghép khối đa diện.

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây:

Bài giảng Toán 12 Bài 1: Khái niệm về khối đa diện

PHÂN CHIA, LẮP GHÉP KHỐI ĐA DIỆN

A. PHƯƠNG PHÁP GIẢI

Nếu khối đa diện $\left(H\right)$ là hợp của hai khối đa diện $\left(H_1\right),\left(H_2\right)$, sao cho $\left(H_1\right)$ và $\left(H_2\right)$ không có điểm trong chung thì ta nói có thể chia được khối đa diện (H) thành hai khối đa diện $\left(H_1\right)$ và $\left(H_2\right)$, hay có thể lắp ghép được hai khối đa diện $\left(H_1\right)$ và $\left(H_2\right)$ với nhau để được khối đa diện $\left(H\right)$.

Ví dụ. Xét khối lập phương $ABCD.A\text{'}B\text{'}C\text{'}D\text{'}$. Mặt phẳng $BDD\text{'}B\text{'}$ cắt khối lập phương đó theo một thiết diện là hình chữ nhật $BDD\text{'}B\text{'}$. Thiết diện này chia các điểm còn lại của khối lập phương ra làm hai phần. Mỗi phần cùng với hình chữ nhật $BDD\text{'}B\text{'}$ tạo thành khối lăng trụ, như vậy có hai khối lăng trụ: $ABD.A\text{'}B\text{'}D\text{'}$ và $BCD.B\text{'}C\text{'}D\text{'}$. Khi đó ta nói mặt phẳng  chia khối lập phương $ABCD.A\text{'}B\text{'}C\text{'}D\text{'}$ thành hai khối lăng trụ $ABD.A\text{'}B\text{'}D\text{'}$ và $BCD.B\text{'}C\text{'}D\text{'}$.

Tương tự trên ta có thể chia tiếp khối trụ $ABD.A\text{'}B\text{'}D\text{'}$ thành ba khối tứ diện: $ADBB\text{'},ADB\text{'}D\text{'}$ và $AA\text{'}B\text{'}D\text{'}$.

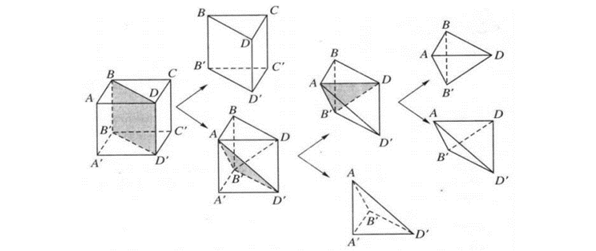
Nhận xét: Một khối đa diện bất kì luôn có thể phân chia được thành các khối tứ diện.

MỘT SỐ KẾT QUẢ

Kết quả 1: Một khối đa diện bất kì có ít nhất 4 mặt.

Kết quả 2: Mỗi hình đa diện có ít nhất 4 đỉnh.

Kết quả 3: Mỗi hình đa diện có ít nhất 6 cạnh.

Kết quả 4: Mỗi đỉnh của một hình đa diện là đỉnh chung của ít nhất 3 cạnh.

Kết quả 5: Không tồn tại hình đa diện có 7 cạnh.

Kết quả 6: Cho $\left(H\right)$ là đa diện mà các mặt của nó là những đa giác có p cạnh. Nếu số mặt của $\left(H\right)$ là lẻ thì p phải là số chẵn.

Chứng minh: Gọi M là số các mặt của khối đa diện $\left(H\right)$. Vì mỗi mặt của $\left(H\right)$ có  cạnh nên M mặt sẽ có $p.M$ cạnh. Nhưng do mỗi cạnh là cạnh chung của đúng hai đa giác nên số cạnh của $\left(H\right)$ bằng $C=\frac{pM}{2}$. Vì M lẻ nên p phải là số chẵn.

Kết quả 7 (Suy ra từ chứng minh kết quả 6): Cho $\left(H\right)$ là đa diện có M mặt, mà các mặt của nó là những đa giác có p cạnh. Khi đó số cạnh của $\left(H\right)$ là $C=\frac{pM}{2}$.

Kết quả 8: Mỗi khối đa diện có các mặt là các tam giác thì tổng số các mặt của nó phải là một số chẵn.

Chứng minh: Gọi số cạnh và số mặt của khối đa diện lần lượt là C và M

Vì mỗi mặt có ba cạnh và mỗi cạnh là cạnh chung của đúng hai mặt nên ta có số cạnh của đa diện là $C=\frac{3M}{2}\stackrel{C\in \mathbb{Z}}{\to }M$ chẵn.

Kết quả 9: Mỗi khối đa diện bất kì luôn có thể được phân chia được thành những khối tứ diện.

Kết quả 10: Nếu khối đa diện có mỗi đỉnh là đỉnh chung của ba cạnh thì số đỉnh phải là số chẵn. (Tổng quát: Một đa diện mà mỗi đỉnh của nó đều là đỉnh chung của một số lẻ mặt thì tổng số đỉnh là một số chẵn).

B. BÀI TẬP TỰ LUYỆN

Câu 1. Một đứa trẻ dán  hình lập phương cạnh $1cm$ lại với nhau, tạo thành một khối hộp có mặt hình chữ nhật. Nếu chu vi đáy là $18cm$ thì chiều cao của khối hộp là:

             A. 3.                         B. 7.                         C. 6.                         D. 2.

Câu 2. Một hình lập phương có cạnh $4cm$ Người ta sơn đỏ mặt ngoài của hình lập phương rồi cắt hình lập phương bằng các mặt phẳng song song với các mặt của hình lập phương thành 64 hình lập phương nhỏ có cạnh $1cm$ Có bao nhiêu hình lập phương có đúng một mặt được sơn đỏ?

             A. 48.                       B. 8.                         C. 24.                        D. 16.

Câu 3. Cho khối tứ diện $ABCD$. Lấy điểm M nằm giữa A và B, điểm N nằm giữa C và D. Bằng hai mặt phẳng $\left(CDM\right)$ và $\left(ABN\right)$, ta chia khối tứ diện đó thành bốn khối tứ diện nào sau đây?

             A. $NACB$, $BCMN$, $ABND$, $MBND$.                B. $MANC$, $BCDN$, $AMND$, $ABND$.

             C. $MANC$, $BCMN$, $AMND$, $MBND$.               D. $ABCN$, $ABND$, $AMND$, $MBND$.

Câu 4. Cắt khối trụ $ABC.A^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}$ bởi các mặt phẳng $\left(A{B}^{\text{'}}{C}^{\text{'}}\right)$ và $\left(AB{C}^{\text{'}}\right)$ ta được những khối đa diện nào?

             A. Ba khối tứ diện.                                      B. Hai khối tứ diện và hai khối chóp tứ giác.

             C. Hai khối tứ diện và một khối chóp tứ giác.     D. Một khối tứ diện và hai khối chóp tứ giác.

Câu 5. Cắt khối lăng trụ $MNP.M^{\text{'}}{N}^{\text{'}}{P}^{\text{'}}$ bởi các mặt phẳng $\left(M{N}^{\text{'}}{P}^{\text{'}}\right)$ và $\left(MN{P}^{\text{'}}\right)$ ta được những khối đa diện nào?

             A. Hai khối tứ diện và một khối chóp tứ giác.     B. Hai khối tứ diện và hai khối chóp tứ giác.

             C. Một khối tứ diện và một khối chóp tứ giác.    D. Ba khối tứ diện.