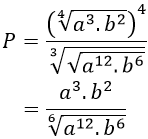Phương pháp giải về Rút gọn biểu thức lũy thừa 2024 (lý thuyết và bài tập)

Quý Lê Xuân Ngày: 28-10-2024 Lớp 12

Tải xuống 4 7.1 K 36

Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu Rút gọn biểu thức lũy thừa Toán lớp 12, tài liệu bao gồm 4 trang có phương pháp giải chi tiết và bài tập, giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kì thi THPT môn Toán sắp tới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Tài liệu Bài tập Rút gọn biểu thức lũy thừa gồm các nội dung chính sau:

A. Phương phương giải

- Gồm phương pháp giải Rút gọn biểu thức lũy thừa.

B. Bài tập

- Gồm 21 bài tập có đáp án và lời giải chi tiết giúp học sinh tự rèn luyện cách giải các dạng Bài tập Rút gọn biểu thức lũy thừa.

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây:

Bài giảng Toán học 12 Bài 1: Lũy thừa

RÚT GỌN BIỂU THỨC LŨY THỪA

A. PHƯƠNG PHÁP GIẢI

Cho hai số dương a; b và $m; n \in ℝ$ . Khi đó ta có các công thức sau.

Nhóm công thức 1

Nhóm công thức 2

1. $a^{m} . a^{n} = a^{m + n}$

2. $\frac{a^{m}}{a^{n}} = a^{m - n} (m = 0 \Leftrightarrow \frac{1}{a^{n}} = a^{- n})$

3. ${(a^{m})}^{n} = a^{m . n}$

1. $a^{\frac{m}{n}} = \sqrt[n]{a^{m}} = {(\sqrt[n]{a})}^{m}$

2. $a^{n} . b^{n} = {(a b)}^{n}, \sqrt[n]{a} . \sqrt[n]{b} = \sqrt[n]{a b}$

3. $\frac{a^{n}}{b^{n}} = {(\frac{a}{b})}^{n}, \frac{\sqrt[n]{a}}{\sqrt[n]{b}} = \sqrt[n]{\frac{a}{b}}$

Tính chất 1: $a^{0} = 1 (a \neq 0)$ và $a^{1} = a$ .

Tính chất 2 (tính đồng biến, nghịch biến): $[\begin{array}{l} a > 1; a^{m} > a^{n} \Leftrightarrow m > n \\ 0 < a < 1 : a^{m} > a^{n} \Leftrightarrow m < n \end{array}$ .

Tính chất 3 (so sánh lũy thừa khác cơ số): Với $a > b > 0$ thì $[\begin{array}{l} a^{m} > b^{m} \Leftrightarrow m > 0 \\ a^{m} < b \Leftrightarrow m < 0 \end{array}$ .

B. BÀI TẬP

Ví dụ 1: Cho biểu thức $P = \sqrt{x . \sqrt[3]{x^{2} . \sqrt{x^{3}}}}$ , với $x > 0$ . Mệnh đề nào sau đây là đúng?

A. $P = x^{\frac{13}{12}}$ . B. $P = x^{\frac{13}{24}}$ . C. $P = x^{\frac{13}{6}}$ . D. $P = x^{\frac{13}{8}}$ .

Ví dụ 2: Biết rằng $\sqrt{x} . \sqrt[3]{x^{2} . \sqrt{x}} = x^{n}$ với $x > 0$ . Tìm n.

A. $n = 2$ . B. $n = \frac{2}{3}$ . C. $n = \frac{4}{3}$ . D. $n = 3$ .

Ví dụ 3: Cho biểu thức $P = \sqrt{x . \sqrt[3]{x^{2} . \sqrt[k]{x^{3}}}}$ , với $x > 0$ . Biết rằng $P = x^{\frac{23}{24}}$ , giá trị của k bằng:

A. $k = 6$ . B. $k = 2$ . C. $k = 3$ . D. $k = 4$ .

Ví dụ 4: Cho biểu thức $P = \frac{a^{2 + \sqrt{3}} . {(a^{1 - \sqrt{3}})}^{1 + \sqrt{3}}}{a^{1 + \sqrt{3}}}$ , với $a > 0$ . Mệnh đề nào sau đây là đúng?

A. $P = a^{\sqrt{3}}$ . B. $P = \frac{1}{a}$ . C. $P = a$ . D. $P = \frac{1}{a^{\sqrt{3}}}$ .

Ví dụ 5: Cho biểu thức $P = \sqrt[3]{\frac{a}{b} . \sqrt[4]{\frac{b}{a} \sqrt{\frac{a}{b}}}} = {(\frac{a}{b})}^{m}$ với $a; b > 0$ . Tìm m.

A. $m = \frac{7}{24}$ . B. $m = \frac{7}{12}$ . C. $m = - \frac{7}{12}$ . D. $m = - \frac{7}{24}$ .

Ví dụ 6: Cho biểu thức $Q = \frac{a^{\frac{7}{6}} . b^{\frac{1}{3}}}{\sqrt[6]{a b^{2}}}$ với $a; b > 0$ . Mệnh đề nào sau đây là đúng?

A. $Q = a$ . B. $Q = \frac{a}{b}$ . C. $Q = a b$ . D. $Q = a \sqrt{b}$ .

Ví dụ 7: Cho x là số thực dương, viết biểu thức $Q = \sqrt{x . \sqrt[3]{x^{2}}} . \sqrt[6]{x}$ dưới dạng lũy thừa với số hữu tỉ

A. $Q = x^{\frac{5}{36}}$ . B. $Q = x^{\frac{2}{3}}$ . C. $Q = x$ . D. $Q = x^{2}$ .

Ví dụ 8: Cho biểu thức $P = \sqrt[3]{x . \sqrt[4]{x^{2} . \sqrt{x^{3}}}}$ với $x > 0$ . Mệnh đề nào dưới đây là đúng?

A. $T = a^{4} . b^{6}$ . B. $T = a^{6} . b^{6}$ . C. $T = a^{4} . b^{4}$ . D. $T = a^{6} . b^{4}$ .

Ví dụ 9: Đơn giản biểu thức 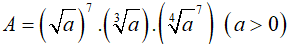Cách giải bài tập Rút gọn biểu thức chứa lũy thừa cực hay ta được:

Cách giải bài tập Rút gọn biểu thức chứa lũy thừa cực hay

Lời giải:

Đáp án: D

Ta có:

Cách giải bài tập Rút gọn biểu thức chứa lũy thừa cực hay

Ví dụ 10: Tính giá trị 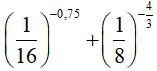Cách giải bài tập Rút gọn biểu thức chứa lũy thừa cực hay , ta được :

A. 12 B. 16 C. 18 D. 24

Lời giải:

Đáp án: D

Ta có:

Cách giải bài tập Rút gọn biểu thức chứa lũy thừa cực hay

Ví dụ 11: Cho a và b là các số dương. Rút gọn biểu thức 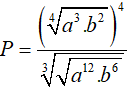Cách giải bài tập Rút gọn biểu thức chứa lũy thừa cực hay được kết quả là :

A. ab² B. a²b C. ab D. a²b²

Lời giải:

Đáp án: C

Ta có:

Cách giải bài tập Rút gọn biểu thức chứa lũy thừa cực hay

Xem thêm

Trang 1

Trang 2

Trang 3

Trang 4

Tài liệu có 4 trang. Để xem toàn bộ tài liệu, vui lòng tải xuống

Từ khóa :

Đánh giá

0 đánh giá

Đánh giá

Tìm kiếm

Tài Liệu Xem Nhiều

pdf Góc giữa cạnh bên và mặt đáy
3 41.5 K 81
pdf Các công thức mặt nón, mặt cầu, mặt trụ
2 40.1 K 85
pdf Dạng bài tập Khảo sát và vẽ đồ thị hàm hữu tỉ bậc hai trên bậc nhất
10 37.3 K 206
pdf 50 Bài tập Nguyên hàm (có đáp án)- Toán 12
22 31.2 K 460
pdf Vị trí tương đối của đường thẳng và mặt phẳng
9 30.3 K 37