Tailieumoi.vn xin giới thiệu Bài tập Toán 12 Chương 2 Bài 1: Luỹ thừa. Bài viết gồm 50 bài tập với đầy đủ các mức độ và có hướng dẫn giải chi tiết sẽ giúp học sinh ôn luyện kiến thức và rèn luyện kĩ năng làm bài tập Toán 12. Ngoài ra, bài viết còn có phần tóm tắt nội dung chính lý thuyết Chương 2 Bài 1: Luỹ thừa. Mời các bạn đón xem:
Bài tập Toán 12 Chương 2 Bài 1: Lũy thừa
A. Bài tập Luỹ thừa
I. Bài tập trắc nghiệm
Bài 1: Biểu thức 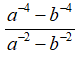
A. a-2 + b-2
B. a-2 - b-2
C. a2 + b2
D. a-6 - b-6
Lời giải:
Sử dụng hằng đẳng thức α2 - β2 = (α + β)(α - β), ta có
Chọn đáp án A.
Bài 2: Cho a và b là 2 số dương thỏa mãn đồng thời ab = ba và b=9a. Tìm a.
Lời giải:
Thế b=9a vào đẳng thức còn lại ta được
a9a = (9a)a => (a9)a => a9 = 9a => a8 = 9 ( do a > 0)
Chọn đáp án B
Bài 3: Biết (a + a-1)2 = 3. Tính giá trị của a3 + a-3 .
A.0
B. 1
C. 2
D. 3.
Lời giải:
Sử dụng hằng đẳng thức ta có
Mặt khác
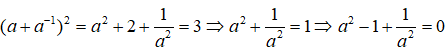
=> a3 + a-3 .Chọn đáp án A.
Bài 4: Biết rằng x = 1 + 2t và y = 1 + 2-t . Hãy biểu diễn y theo x.
Lời giải:
Từ giả thiết ta có x - 1 = 2t
Chọn đáp án D.
Bài 5: Biểu thức 2222 có giá trị bằng
A. 28
B. 216
C. 162
D. 44
Lời giải:
2222 = 224 = 216 (24 = 16)
Chọn đáp án B
Bài 6:
A.
B. -
C.
D. 16.
Lời giải:
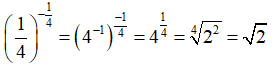
Chọn đáp án A
Bài 7: Tính giá trị của biểu thức
Lời giải:
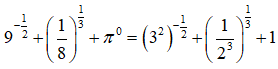
Chọn đáp án D
Bài 8: Giá trị của biểu thức nào sau đây bằng 0,0000000375?
Lời giải:
Viết lại 0,0000000375 = 375.1010 . Trong các số ở các phương án có
()10-7 = 0,735.10-7 = 375.10-10
Chọn đáp án C
Bài 9: Tính giá trị biểu thức 2560,16.2560,09
A.4
B. 16
C. 64
D. 256,25.
Lời giải:
Chọn đáp án A
Bài 10: Rút gọn biểu thức
Lời giải:
Chọn đáp án D
II. Bài tập tự luận có lời giải
Bài 1: Tính giá trị biểu thức
Lời giải:
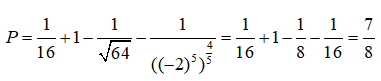
Bài 2: Rút gọn biểu thức
viết kết quả sao cho các lũy thừa đều dương
Lời giải:
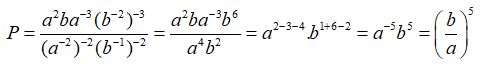
Bài 3: Nếu x > y > 0 thì
Lời giải:
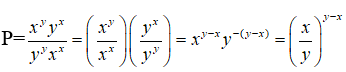
Bài 4: Với x ≥ 0 thì 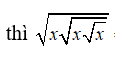
Lời giải:
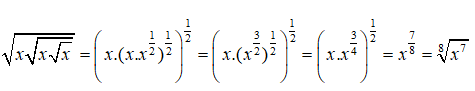
Bài 5: Biểu thức a3 + a-3 bằng
Lời giải:
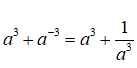
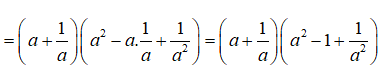
Bài 6: Nếu 21998 - 21997 - 21996 + 21995 = k.21995 thì giá trị của k là?
Lời giải:
21998 - 21997 - 21996 + 21995 = 21995(23 - 22 - 2 + 1)
= 3.21995 = k.21995 => k = 3
Bài 7: Cho a,b,x là các số dương thỏa mãn (2a)2b = ab.xb . Khi đó x bằng
Lời giải:
(2a)2b = ab.xb ⇔ [(2a)2 ]b = (a.x>b)
⇒(4a2)b = (ax)b ⇒ 4a2 = ax ⇒ x = 4a
Bài 8: Trong phòng thí nghiệm, khối lượng của 50 giọt máu cân được là 0,532 gam. Biết rằng khối lượng riêng của máu là 1060kg/m3 và các giọt máu đều là hình cầu có khối lượng bằng nhau.Tính đường kính của giọt máu.
Lời giải:
Bài 9: Tính số nguyên n lớn nhất thỏa mãn n200 < 5300 .
Lời giải:
Ta tìm n trong các số nguyên dương. Khi đó
n200 < 5300 <=> (n2)100 < (53)100 <=> n2 < 53 = 125 <=> n < ≈ 11,18
Ta thấy số nguyên dương n lớn nhất thỏa mãn là n = 11
Bài 10: Giả sử a là số thỏa mãn a + a-1 = 4 .Tính giá trị của biểu thức a4 + a-4.
Lời giải:
a + a-1 = 4 ⇔ 16 = (a + a-1)2 = a2 + 2 + a-2 ⇒ 14 = a2 + a-2
=> 196 = (a2 + a-2)2 = a4 + 2 + a-4 => a4 + a-4 = 194
III. Bài tập vận dụng
Bài 1 Cho 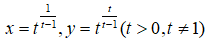
Bài 2 Rút gọn biểu thức
Bài 3 Rút gọn biểu thức:
Bài 4 Biểu thức (x-1 + y-1)-1 bằng?
Bài 5 Nếu 102y = 25 thì 10-y bằng?
Bài 6 Rút gọn biểu thức P = 23.a3b2.(2a-1b2)-2
Bài 7
Bài 8 Tính (1,5)4; ()3; ()5.
Bài 9 Dựa vào đồ thị của các hàm số y = x3 và y = x4 (H.26, H.27), hãy biện luận theo b số nghiệm của các phương trình x3 = b và x4 = b.
Bài 10 Chứng minh tính chất . = .
B. Lý thuyết Luỹ thừa
I. Khái niệm lũy thừa
1. Lũy thừa với số mũ nguyên
Cho n là một số nguyên dương.
Với a là số thực tùy ý, lũy thừa bậc n của a là tích của n thừa số a.
an = a.a.a… a (n thừa số a)
Với a ≠ 0, ta có: a0 = 1 và
Trong biểu thức am ; ta gọi a là cơ số, số nguyên m là số mũ.
– Chú ý:
00 và 0–n không có nghĩa.
Lũy thừa với số mũ nguyên có các tính chất tương tự của lũy thừa với số mũ nguyên dương.
Ví dụ 1. Tính giá trị biểu thức:
Lời giải:
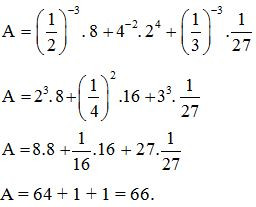
2. Phương trình xn = b.
Đồ thị của hàm số y = x2k + 1 có dạng tương tự đồ thị hàm số y = x3 và đồ thị hàm số y = x2k có dạng tương tự đồ thị hàm số y = x4.
Từ đó, ta có kết quả biện luận số nghiệm của phương trình xn = b như sau:
a) Trường hợp n lẻ:
Với mọi số thực b, phương trình có nghiệm duy nhất.
b) Trường hợp n chẵn:
Với b < 0, phương trình vô nghiệm.
Với b = 0 , phương trình có một nghiệm x = 0.
Với b > 0, phương trình có hai nghiệm đối nhau.
3. Căn bậc n
a) Khái niệm: Cho số thực b và số nguyên dương n . Số a được gọi là căn bậc n của số b nếu an = b.
Ví dụ 2. Căn bậc ba của 27 là 3.
Căn bậc bốn của 256 là 4 và – 4.
– Từ định nghĩa và kết quả biện luận về số nghiệm của phương trình xn = b; ta có:
Với n lẻ và b: Có duy nhất một căn bậc n của b, kí hiệu là .
Với n chẵn và :
+ b < 0 : không tồn tại căn bậc n của b.
+ b = 0: có một căn bậc n của b là số 0.
+ b > 0: có hai căn trái dấu; kí hiệu giá trị dương là ; còn giá trị âm là
b) Tính chất của căn bậc n
Từ định nghĩa ta có các tính chất sau:
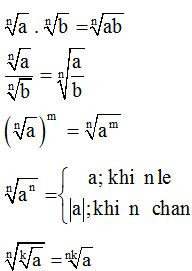
Ví dụ 3. Rút gọn các biểu thức:
a) ;
b) .
Lời giải:
a)
b)
4. Lũy thừa với số mũ hữu tỉ.
– Cho số thực a dương và số hữu tỉ ; trong đó . Lũy thừa của a với số mũ r là số ar xác định bởi: .
Ví dụ 4.
5. Lũy thừa với số mũ vô tỉ.
Cho a là một số dương, α là một số vô tỉ. Ta thừa nhận rằng, luôn có một dãy số hữu tỉ (rn) có giới hạn là α và dãy số tương ứng có giới hạn không phụ thuộc vào việc chọn dãy số (rn).
– Ta gọi giới hạn của dãy số là thừa số của a với số mũ α, kí hiệu là aα.
với .
– Chú ý: Từ định nghĩa, ta có:
II. Tính chất lũy thừa với số mũ thực.
Cho a; b là những số thực dương, α, β là những số thực tùy ý. Khi đó, ta có:
Nếu a > 1 thì khi và chỉ khi α > β.
Nếu a < 1 thì khi và chỉ khi α < β.
Ví dụ 5. Rút gọn biểu thức:
với a > 0.
Lời giải:
Với a > 0 ta có:
Ví dụ 6. So sánh các số và .
Lời giải:
Ta có: và
Suy ra: < .