Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu Chuyên đề các định hệ số của hàm số khi biết bảng biến thiên hoặc đồ thị, tài liệu bao gồm 31 trang. Tài liệu được tổng hợp từ các tài liệu ôn thi hay nhất  giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kỳ thi sắp hới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây

Chuyên đề các định hệ số của hàm số khi biết bảng biến thiên hoặc đồ thị

Xác định hệ số của hàm số khi biết bảng biến thiên hoặc đồ thị

Ví dụ minh họa và phương pháp giải toán

ĐỀ MINH HỌA TỐT NGHIỆP THPT 2020: Cho hàm số \(f(x) = \frac{{ax + 1}}{{bx + c}}(a,b,c \in \mathbb{R})\) có bảng biến thiên như sau:

Trong các số a, b và c có bao nhiêu số dương?

A. 2 .

B. 3 .

C. 1 .

D. 0 .

Phân tích và hướng dẫn giải

1. Dạng toán: Đây là bài toán ở dạng vận dụng: Từ bảng biến thiên xác định dấu các hệ số a, b và c của hàm số \(f(x) = \frac{{ax + 1}}{{bx + c}}\).

2. Kiến thức cần nhớ:

Cho hàm số \(f(x) = \frac{{ax + b}}{{cx + d}}\)

Đồ thị hàm số \(f(x) = \frac{{ax + b}}{{cx + d}}\) có tiệm cận đứng là đường thẳng \(x =  - \frac{d}{c}\).

Đồ thị hàm số \(f(x) = \frac{{ax + b}}{{cx + d}}\) có tiệm cận ngang là đường thẳng \(y = \frac{a}{c}\).

Đạo hàm của hàm số \(f(x) = \frac{{ax + b}}{{cx + d}}\) là \({f^\prime }(x) = \frac{{ad - bc}}{{{{(cx + d)}^2}}}\).

3. Hướng giải:

B1: Từ công thức của hàm số \(f(x) = \frac{{ax + 1}}{{bx + c}}\) chỉ ra phương trình đường thẳng của tiệm cận đứng, tiệm cận ngang và công thức tính đạo hàm của nó.

B2: Từ bảng biến thiên chỉ ra tiệm cận đứng, tiệm cận ngang của đồ thị hàm số và chiều biến thiên của hàm số đó.

B3: Thay các dữ kiện ở bước 1 vào bước 2 ta sẽ xác định được dấu của các hệ số a, b và c.

Từ đó, ta có thể giải bài toán cụ thể như sau:

Lời giải chi tiết

Chọn C

Đồ thị hàm số \(f(x) = \frac{{ax + 1}}{{bx + c}}\) có đường tiệm cận đứng là đường thẳng \(x =  - \frac{c}{b}\) và đường tiệm cận ngang là đường thẳng \(y = \frac{a}{b}\).

Từ bảng biến thiên ta có: \(\left\{ {\begin{array}{*{20}{l}}{ - \frac{c}{b} = 2}\\{\frac{a}{b} = 1}\end{array} \Leftrightarrow a = b =  - \frac{c}{2}(1)} \right.\)

Mặt khác: \({f^\prime }(x) = \frac{{ac - b}}{{{{(bx + c)}^2}}}\).

Vì hàm số đã cho đồng biến trên các khoảng \(( - \infty ;2)\) và \((2; + \infty )\) nên

\({f^\prime }(x) = \frac{{ac - b}}{{{{(bx + c)}^2}}} > 0 \Leftrightarrow ac - b > 0\)

Thay (1) vào (2), ta được: \( - \frac{{{c^2}}}{2} + \frac{c}{2} > 0 \Leftrightarrow  - {c^2} + c > 0 \Leftrightarrow 0 < c < 1\). Suy ra c là số dương và a, b là số âm.

Suy ra c là số dương và a, b

Bài tập tương tự và phát triển – phần 1

Câu 1: Cho hàm số \(f(x) = \frac{{ax + {m^2} + 4}}{{bx + c}}(a,b,c,m \in \mathbb{R})\) có bảng biến thiên như sau:

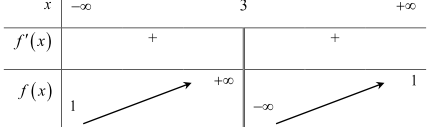
Trong các số a, b và c có bao nhiêu số dương?

A. 2 .

B. 3 .

C. 1 .

D. 0 .

Chon C

Lời giải

Tiệm cận đứng: \(x = 3 > 0 \Rightarrow  - \frac{c}{b} > 0 \Rightarrow bc < 0\).

Tiệm cận ngang: \(y = 1 > 0 \Rightarrow \frac{a}{b} > 0 \Rightarrow ab > 0\).

Đồ thị hàm số cắt trục hoành tại điểm có hoành độ

\(x > 3 > 0 \Rightarrow  - \frac{{{m^2} + 4}}{a} > 0 \Rightarrow a < 0 \Rightarrow b < 0\) \( \Rightarrow c > 0.\)

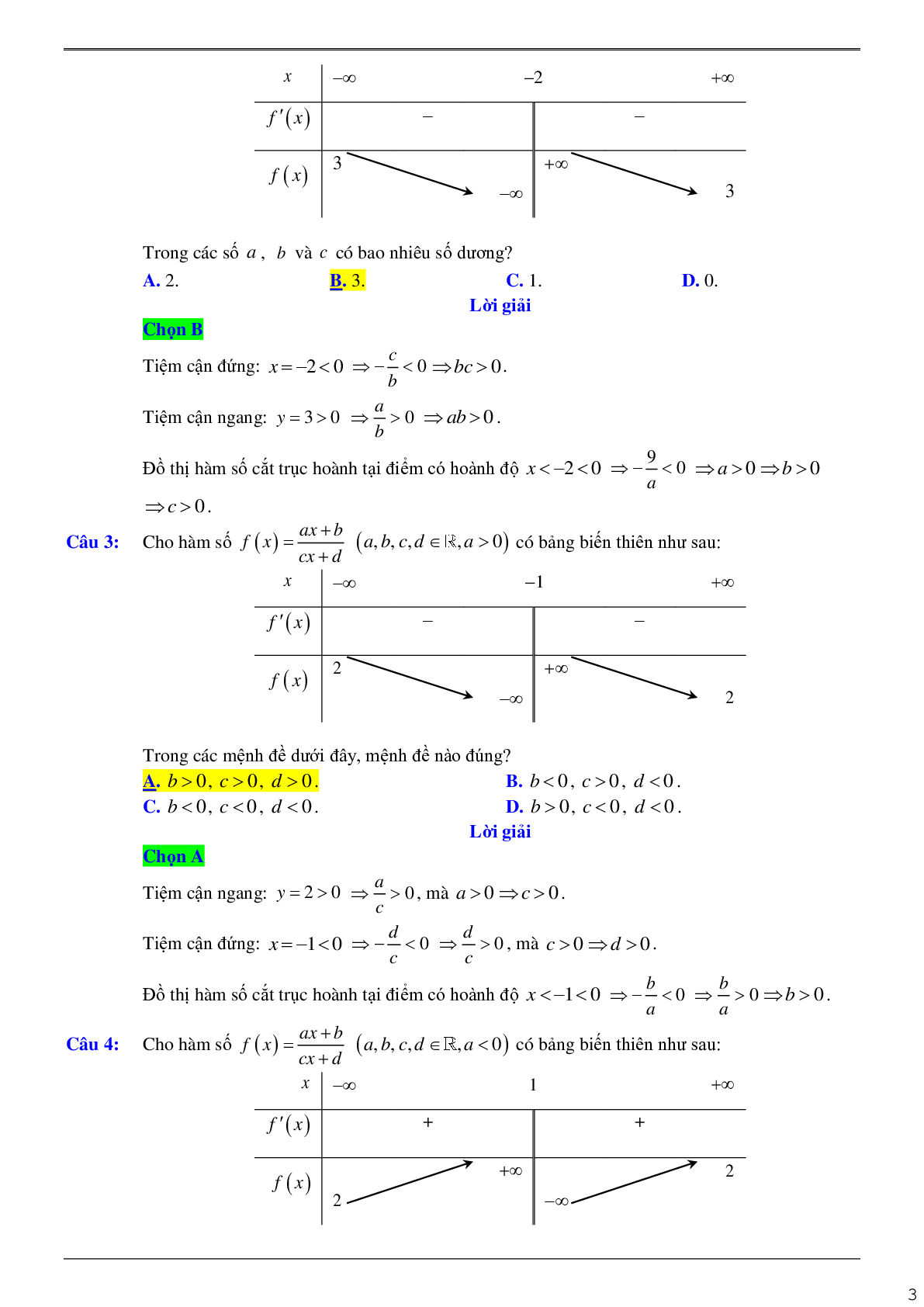
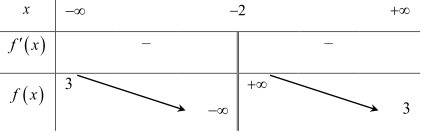
Câu 2: Cho hàm số \(f(x) = \frac{{ax + 9}}{{bx + c}}(a,b,c \in \mathbb{R})\) có bảng biến thiên như sau:

Trong các số a, b và c có bao nhiêu số dương?

A. 2 .

B. 3 .

C. 1 .

D. 0 .

Chọn B

Lời giải

Tiệm cận đứng: \(x =  - 2 < 0 \Rightarrow  - \frac{c}{b} < 0 \Rightarrow bc > 0\).

Tiệm cận ngang: \(y = 3 > 0 \Rightarrow \frac{a}{b} > 0 \Rightarrow ab > 0\).

Đồ thị hàm số cắt trục hoành tại điểm có hoành độ \(x <  - 2 < 0\)

\( \Rightarrow  - \frac{9}{a} < 0 \Rightarrow a > 0 \Rightarrow b > 0\) \( \Rightarrow c > 0\).

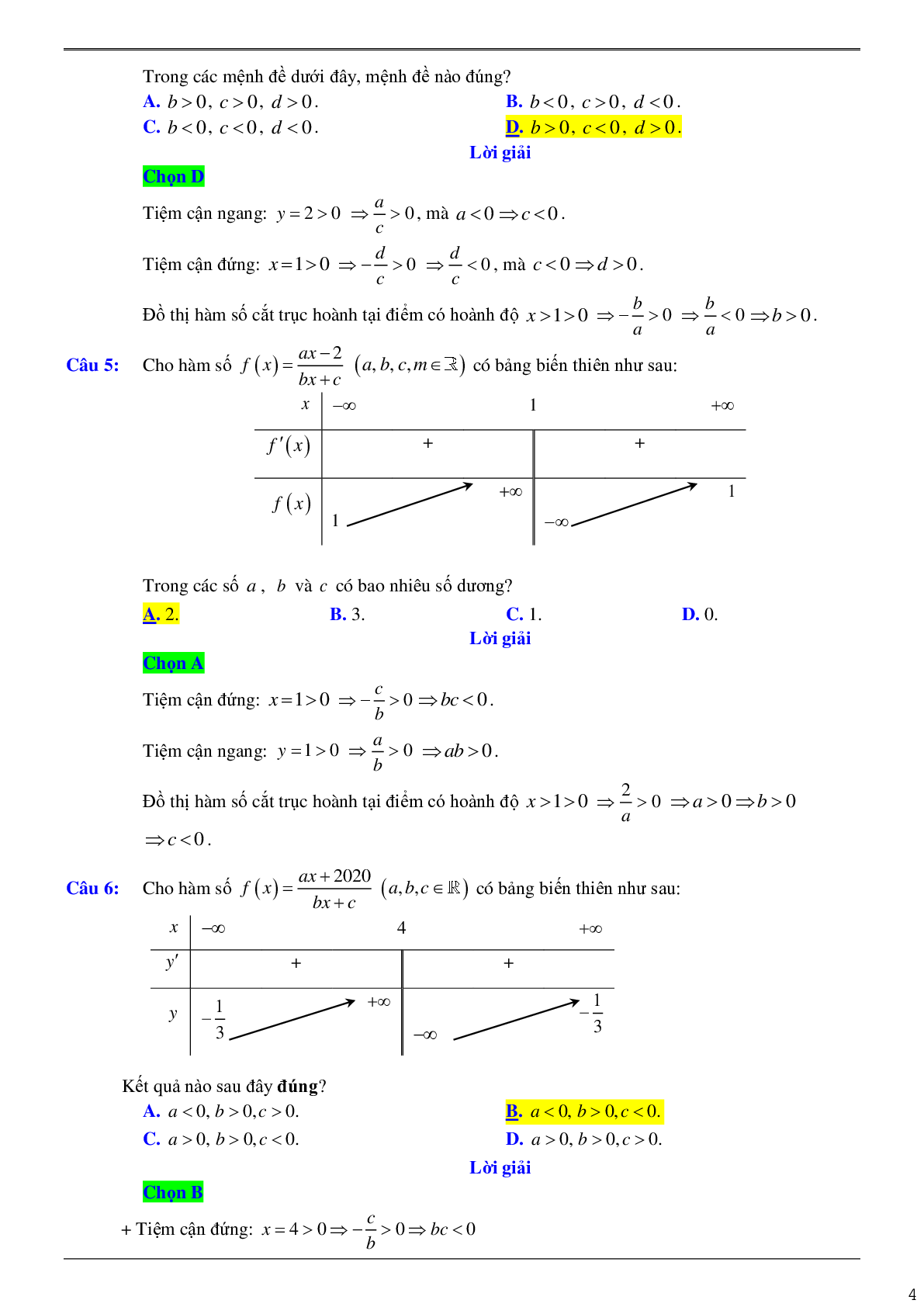
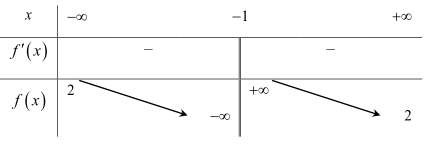
Câu 3: Cho hàm số \(f(x) = \frac{{ax + b}}{{cx + d}}(a,b,c,d \in \mathbb{R},a > 0)\) có bảng biến thiên như sau:

Trong các mệnh đề dưới đây, mệnh đề nào đúng?

A. \(b > 0,c > 0,d > 0\).

B. \(b < 0,c > 0,d < 0\).

C. \(b < 0,c < 0,d < 0\).

D. \(b > 0,c < 0,d < 0\).

Lời giải

Chọn A

Tiệm cận ngang: \(y = 2 > 0 \Rightarrow \frac{a}{c} > 0\), mà \(a > 0 \Rightarrow c > 0\).

Tiệm cận đứng: \(x =  - 1 < 0 \Rightarrow  - \frac{d}{c} < 0 \Rightarrow \frac{d}{c} > 0\), mà \(c > 0 \Rightarrow d > 0\).

Đồ thị hàm số cắt trục hoành tại điểm có hoành độ

\(x <  - 1 < 0 \Rightarrow  - \frac{b}{a} < 0 \Rightarrow \frac{b}{a} > 0 \Rightarrow b > 0\).

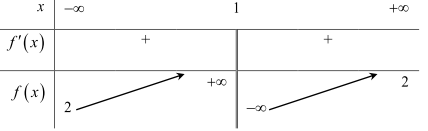
Câu 4: Cho hàm số \(f(x) = \frac{{ax + b}}{{cx + d}}(a,b,c,d \in \mathbb{R},a < 0)\) có bảng biến thiên như sau:

Trong các mệnh đề dưới đây, mệnh đề nào đúng?

A. \(b > 0,c > 0,d > 0\).

B. \(b < 0,c > 0,d < 0\).

C. \(b < 0,c < 0,d < 0\).

D. \(b > 0,c < 0,d > 0\).

Lời giải

Chọn D

Tiệm cận ngang: \(y = 2 > 0 \Rightarrow \frac{a}{c} > 0\), mà \(a < 0 \Rightarrow c < 0\).

Tiệm cận đứng: \(x = 1 > 0 \Rightarrow  - \frac{d}{c} > 0 \Rightarrow \frac{d}{c} < 0\), mà \(c < 0 \Rightarrow d > 0\).

Đồ thị hàm số cắt trục hoành tại điểm có hoành độ

\(x > 1 > 0 \Rightarrow  - \frac{b}{a} > 0 \Rightarrow \frac{b}{a} < 0 \Rightarrow b > 0\).

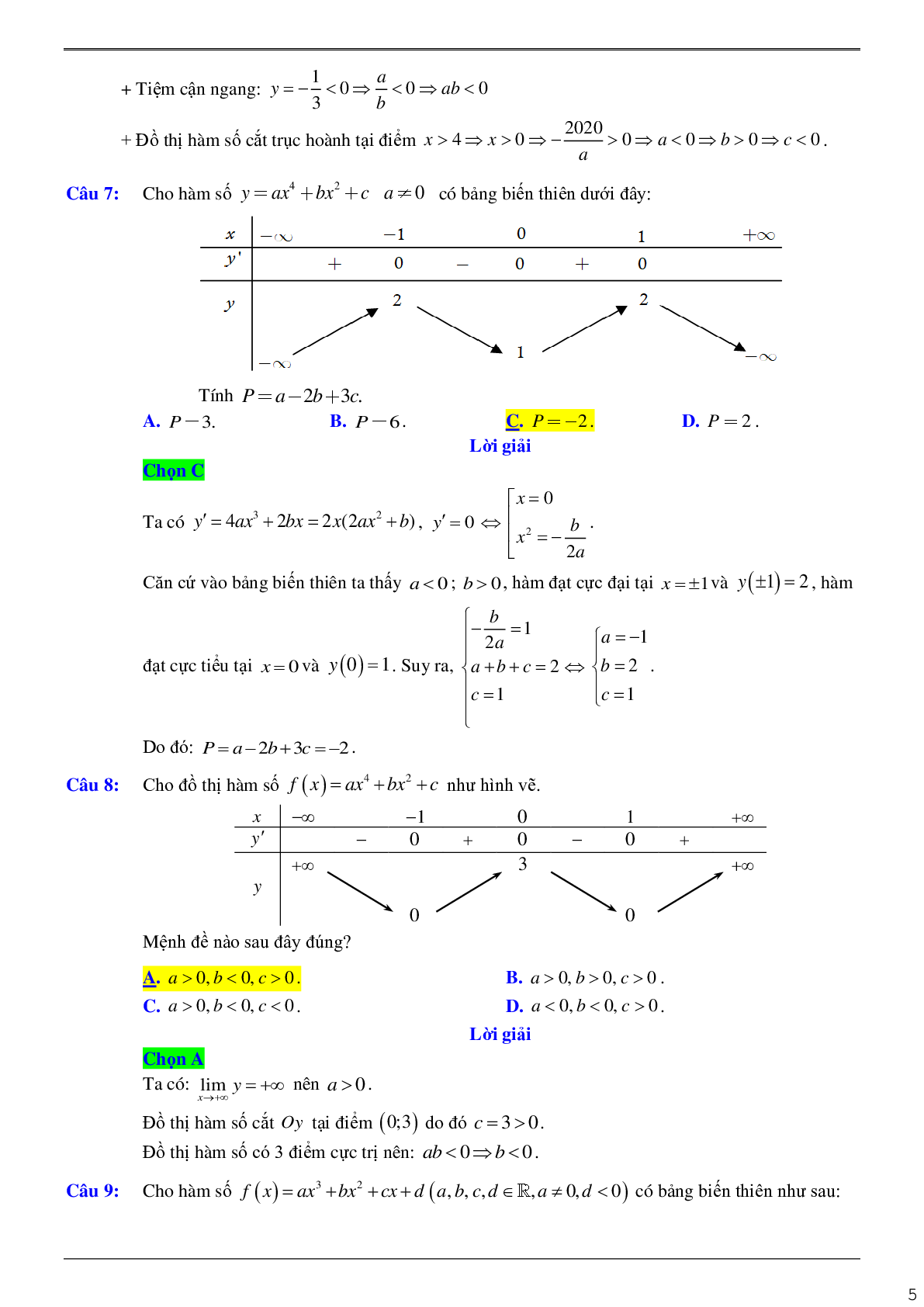
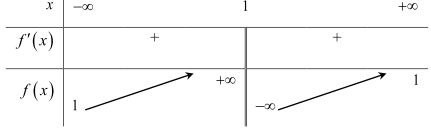
Câu 5: Cho hàm số \(f(x) = \frac{{ax - 2}}{{bx + c}}(a,b,c,m \in \mathbb{R})\) có bảng biến thiên như sau:

Trong các số a, b và c có bao nhiêu số dương?

A. 2 .

B. 3 .

C. 1 .

D. 0 .

Chọn A

Lời giải

Tiệm cận đứng: \(x = 1 > 0 \Rightarrow  - \frac{c}{b} > 0 \Rightarrow bc < 0\).

Tiệm cận ngang: \(y = 1 > 0 \Rightarrow \frac{a}{b} > 0 \Rightarrow ab > 0\).

Đồ thị hàm số cắt trục hoành tại điểm có hoành độ

 \(x > 1 > 0 \Rightarrow \frac{2}{a} > 0 \Rightarrow a > 0 \Rightarrow b > 0\) \( \Rightarrow c < 0\).

Câu 6: Cho hàm số \(f(x) = \frac{{ax + 2020}}{{bx + c}}(a,b,c \in \mathbb{R})\) có bảng biến thiên như sau:

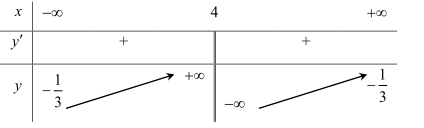
Kết quả nào sau đây đúng?

A. \(a < 0,b > 0,c > 0\).

B. \(a < 0,b > 0,c < 0\).

C. \(a > 0,b > 0,c < 0\).

D. \(a > 0,b > 0,c > 0\).

Lời giải

Chọn B

+ Tiệm cận đứng: \(x = 4 > 0 \Rightarrow  - \frac{c}{b} > 0 \Rightarrow bc < 0\)

+ Tiệm cận ngang: \(y =  - \frac{1}{3} < 0 \Rightarrow \frac{a}{b} < 0 \Rightarrow ab < 0\)

+ Đồ thị hàm số cắt trục hoành tại điểm

\(\begin{array}{l}x > 4 \Rightarrow x > 0 \Rightarrow  - \frac{{2020}}{a} > 0\\ \Rightarrow a < 0 \Rightarrow b > 0 \Rightarrow c < 0\end{array}\).

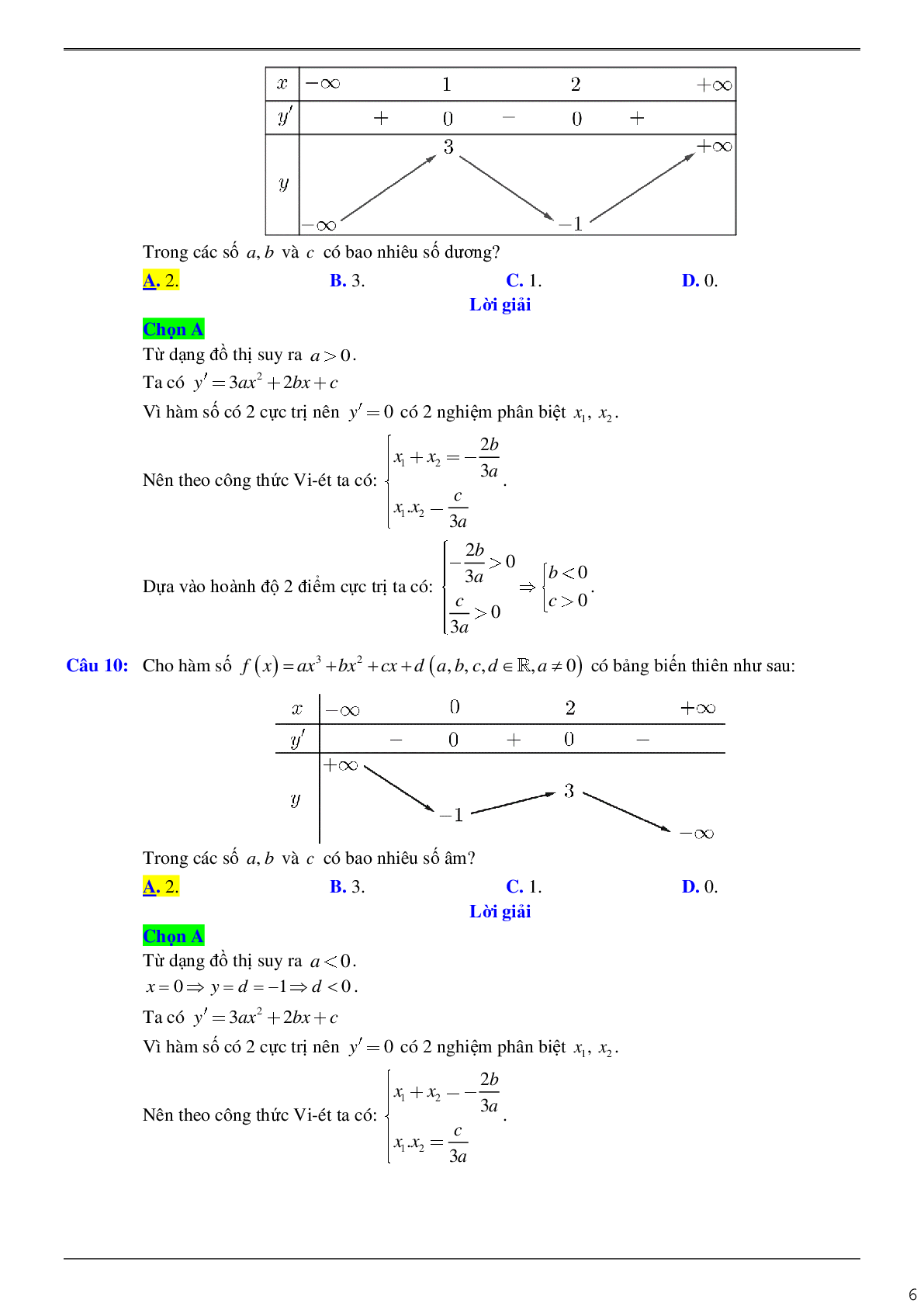
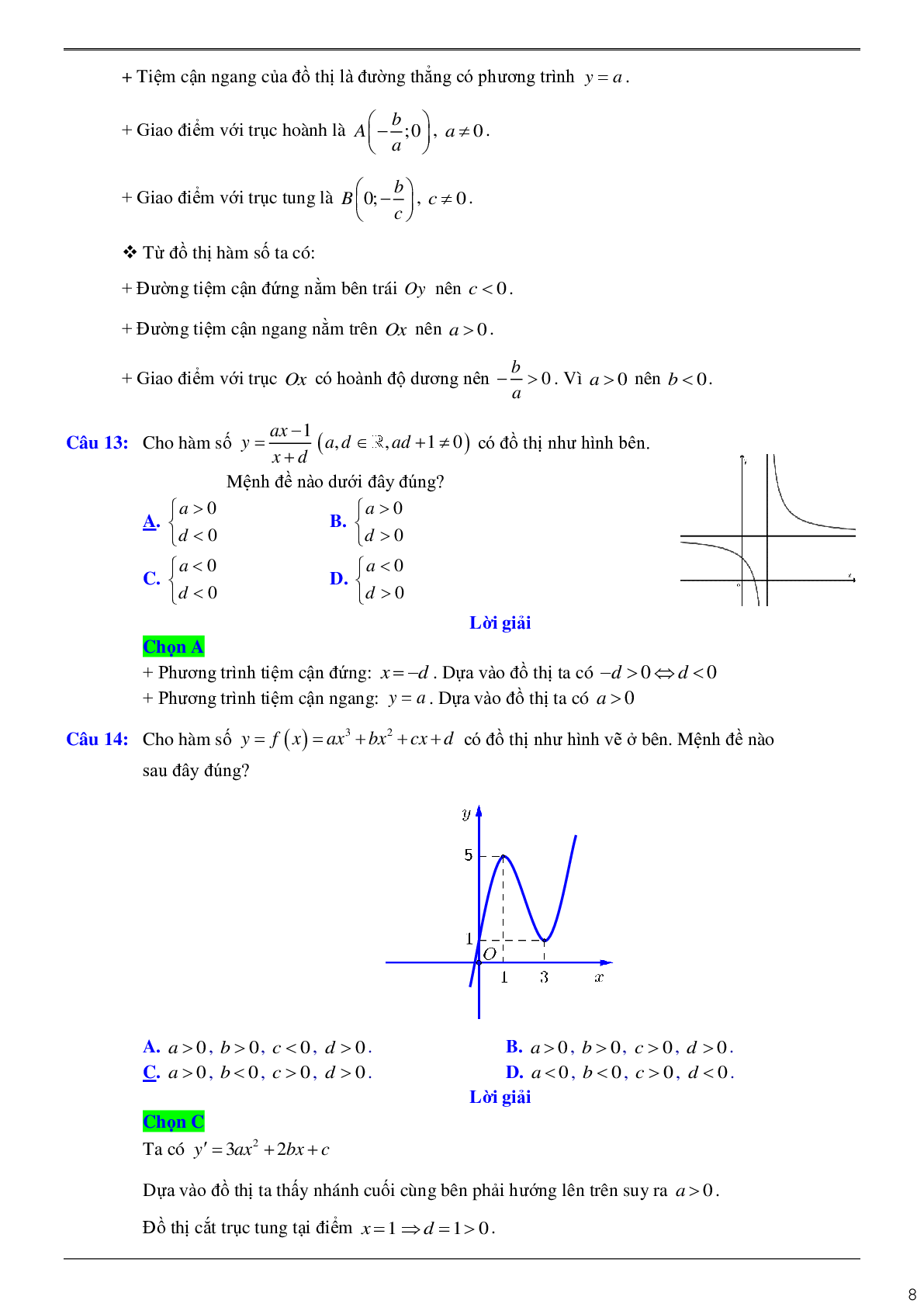
Câu 7: Cho hàm số \(y = a{x^4} + b{x^2} + c\quad a \ne 0\) có bảng biến thiên dưới đây:

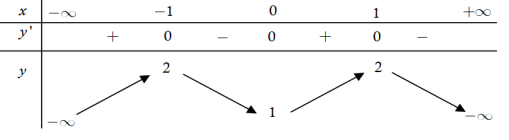
Tính \(P = a - 2b + 3c\).

A. \(P = 3\).

B. \(P = 6\).

C. \(P =  - 2\).

D. \(P = 2\).

Chọn C

Lời giải

Ta có \({y^\prime } = 4a{x^3} + 2bx = 2x\left( {2a{x^2} + b} \right),{y^\prime } = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 0}\\{{x^2} =  - \frac{b}{{2a}}}\end{array}} \right.\).

Căn cứ vào bảng biến thiên ta thấy \(a < 0;b > 0\), hàm đạt cực đại tại \(x =  \pm 1\) và \(y( \pm 1) = 2\), hàm

đạt cực tiểu tại \(x = 0\) và \(y(0) = 1\).

 Suy ra, \(\left\{ {\begin{array}{*{20}{l}}{ - \frac{b}{{2a}} = 1}\\{a + b + c = 2 \Leftrightarrow }\\{c = 1}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{a =  - 1}\\{b = 2}\\{c = 1}\end{array}} \right.} \right.\).

Do đó: \[P = a - 2b + 3c =  - 2\].

Câu 8: Cho đồ thị hàm số \(f(x) = a{x^4} + b{x^2} + c\) như hình vẽ.

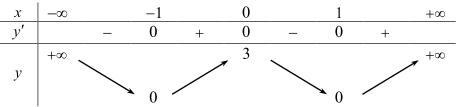
Mệnh đề nào sau đây là đúng?

\[{\rm{\;A}}{\rm{.\;}}a > 0,b < 0,c > 0\]

B. \(a > 0,b > 0,c > 0\).

C. \(a > 0,b < 0,c < 0\).

D. \(a < 0,b < 0,c > 0\).

Lời giải

Chọn A

Ta có: \(\mathop {\lim }\limits_{x \to  + \infty } y =  + \infty \) nên \(a > 0\).

Đồ thị hàm số cắt $O y$ tại điểm \((0;3)\) do đó \(c = 3 > 0\).

Đồ thị hàm số có 3 điểm cực trị nên: \(ab < 0 \Rightarrow b < 0\).

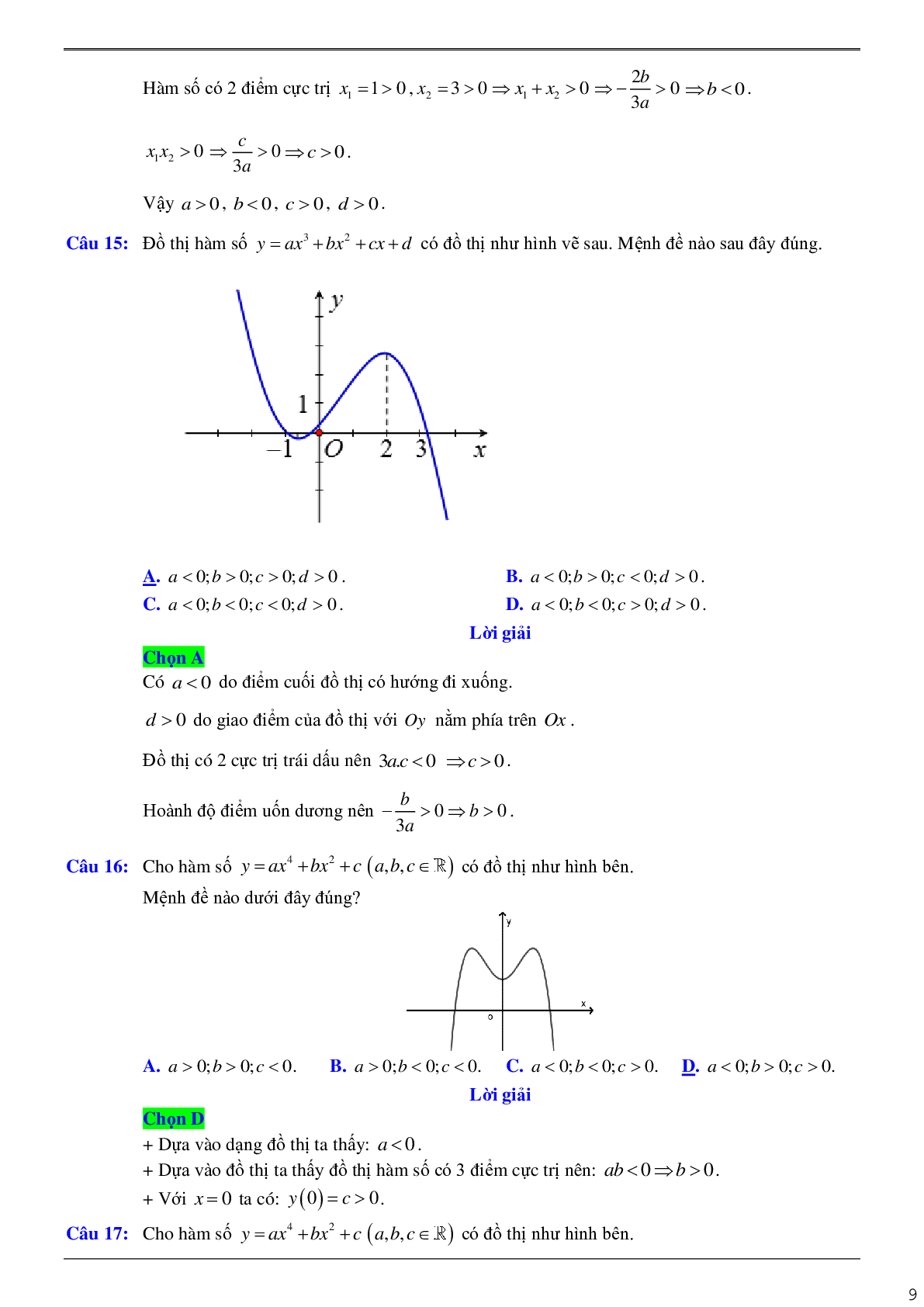
Câu 9: Cho hàm số \(f(x) = a{x^3} + b{x^2} + cx + d(a,b,c,d \in \mathbb{R},a \ne 0,d < 0)\) có bảng biến thiên như sau:

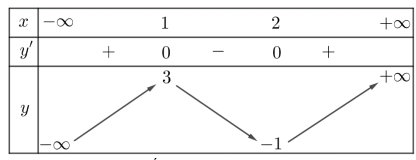
Trong các số a, b và c có bao nhiêu số dương?

A. 2 .

B. 3 .

C. 1 .

D. 0 .