Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu Bài tập Vận dụng cao - Nghiệm của phương trình hàm hợp ôn thi THPTQG năm 2021, tài liệu bao gồm 28 trang. Tài liệu được tổng hợp từ các tài liệu ôn thi hay nhất  giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kỳ thi sắp hới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây

Bài tập Vận dụng cao - Nghiệm của phương trình hàm hợp ôn thi THPTQG năm 2021

Hàm Số và đồ thị phần 1

Câu 1. (THPT Lê Văn Thịnh - Bắc Ninh 2019) Cho hàm số \(y = {x^3} - 3x + 2(C)\). Biết rằng đường thẳng \(d:y = ax + b\) cắt đồ thị (C) tại ba điểm phân biệt M, N, P. Tiếp tuyến tại ba điểm M, N, P của đồ thị (C) cắt (C) tại các điểm \({M^\prime },{N^\prime },{P^\prime }\) (tương ứng khác M, N, P). Khi đường thẳng đi qua ba điểm \(M',N',P'\)có phương trình là.

A. \(y = ax + b\)

B. \(y = (4a + 9)x + 18 - 8b\)

C. \(y =  - (8a + 18)x + 18 - 8b\)

D. \(y = (4a + 9)x + 14 - 8b\)

Lời giải:

 Ta giả sử \(A\left( {m;{m^3} - 3m + 2} \right)\) với \({m^3} - 3m + 2 = am + b\).

Tiếp tuyến tại \(A\) là: \(y = \left( {3{m^2} - 3} \right)(x - m) + {m^3} - 3m + 2\). Xét phương trình hoành độ giao điểm:

\({x^3} - 3x + 2 = \left( {3{m^2} - 3} \right)(x - m) + {m^3} - 3m + 2 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x =  - 2m}\\{x = m}\end{array}} \right.\)

Khi đó giao điểm của tiếp tuyến đó với đồ thị là \({A^\prime }\left( { - 2m; - 8{m^3} + 6m + 2} \right)\).

Lại có:

\(\begin{array}{l} - 8{m^3} + 6m + 2 =  - 8\left( {{m^3} - 3m + 2} \right) - 18m + 18\\ \Rightarrow {y_{{A^\prime }}} =  - 8(am + b) - 18m + 18\end{array}\)

\(\begin{array}{l} \Leftrightarrow {y_{{A^\prime }}} = 4a{x_{{A^\prime }}} + 9{x_{{A^\prime }}} + 18 - 8b\\ \Leftrightarrow {y_{{A^\prime }}} = (4a + 9){x_{{A^\prime }}} + 18 - 8b\end{array}\)

Vậy Chọn B.

Câu 2. (Chuyên Bắc Ninh 2019) Tìm tất cả các giá trị thực của tham số m sao cho phương trình \(3\sqrt {x - 1}  + m\sqrt {x + 1}  = 2\sqrt[4]{{{x^2} - 1}}\) có hai nghiệm thực?

A. \(\frac{1}{3} \le m < 1\)

B. \( - 2 < m \le \frac{1}{3}\)

C. \( - 1 \le m \le \frac{1}{4}\)

D. \(0 \le m < \frac{1}{3}\)

Lời giải

Ta chia 2 vế chp \(\sqrt {x + 1} \) và đặt \(0 \le t = \sqrt[4]{{\frac{{x - 1}}{{x + 1}}}} < 1\) ta suy ra: \(m = 2t - 3{t^2}\). Khảo sát bảng biến thiên ta Chọn D.

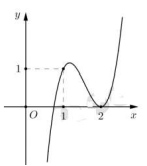
Câu 3. (THPT Lê Văn Thịnh - Bắc Ninh 2019) Cho hàm số bậc ba \(f(x) = a{x^3} + b{x^2} + cx + d\) có đồ thị như hình vẽ bên. Hỏi đồ thị hàm số \(g(x) = \frac{{\left( {{x^2} - 3x + 2} \right)\sqrt {2x - 1} }}{{x\left[ {{f^2}(x) - f(x)} \right]}}\) có bao nhiêu đường tiệm cận đứng?

A. 5

B. 4

C. 6

D. 3

Lời giải

Với f(x ) =0  ta thu được 2 nghiệm thỏa mãn \( \ge \frac{1}{2}\) (áng chừng: \(x = 0,8;x = 2\) ) còn \(f(x) = 1\) thu được 3 nghiệm thỏa mãn \( \ge \frac{1}{2}\) (áng chừng: \(x = 1;x = 1,5;x = 2,5\) ).

Mặt khác dễ thấy \(x = 2\) nghiệm kép và \(x = 1\) nghiệm đơn đồng thời tử số có \({x^2} - 3x + 2 = (x - 1)(x - 2)\) do vậy thực tế ta còn 4 đường tiệm cận đứng đó là \(x = 0,8;x = 2;x = 1,5;x = 2,5\).

Câu 4. (THPT Lê Văn Thịnh - Bắc Ninh 2019) Cho hàm số \(y = \left| {\frac{{{x^4} + ax + a}}{{x + 1}}} \right|\). Gọi M, m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số đã cho trên đoạn [1 ; 2]. Có bao nhiêu giá trị nguyên của a để \(M \ge 2m\).

A. 15

B. 14

C. 13

D. 16

Lời giải

Ta có \(y = \left| {\frac{{{x^4}}}{{x + 1}} + a} \right|\). Chú ý rằng trên [1 ; 2] thì hàm số \(y = \frac{{{x^4}}}{{x + 1}} + a\) đồng biến có min \( = a + \frac{1}{2}\) và có \(\max  = a + \frac{{16}}{3}\). Ta chia làm 3 trường hợp sau:

- Trường họp 1: \(a + \frac{{16}}{3} \le 0;\left| {a + \frac{1}{2}} \right| \ge 2\left| {a + \frac{{16}}{3}} \right| \Rightarrow  - \frac{{61}}{6} \le a \le  - \frac{{16}}{3}\).

- Trường họp 2: \(a + \frac{1}{2} \ge 0;\left| {a + \frac{{16}}{3}} \right| \ge 2\left| {a + \frac{1}{2}} \right| \Rightarrow  - \frac{1}{2} \le a \le \frac{{13}}{3}\).

- Trường họp 3: \(a + \frac{1}{2} \le 0 \le a + \frac{{16}}{3} \Leftrightarrow  - \frac{{16}}{3} \le a \le  - \frac{1}{2}\) thì \(m = 0\) nên \(M \ge 2m\) luôn đúng.

Câu 1: (ĐỀ THAM KHẢO CỦA BỘ GIÁO DỤC 2018) Có bao nhiêu giá trị nguyên của tham số m để phương trình \(\sqrt[3]{{m + 3\sqrt[3]{{m + 3\sin x}}}} = \sin x\) có nghiệm thực?

A. 5 .

B. 7 .

C. 3 .

D. 2 .

Lời giải

Ta có

\(\begin{array}{l}\sqrt[3]{{m + 3\sqrt[3]{{m + 3\sin x}}}} = \sin x\\ \Leftrightarrow 3\sqrt[3]{{m + 3\sin x}} = {\sin ^3}x - m\end{array}\)

\( \Leftrightarrow (m + 3\sin x) + 3\sqrt[3]{{m + 3\sin x}} = {\sin ^3}x + 3\sin x.\)

Suy ra: \(\sqrt[3]{{m + 3\sin x}} = \sin x \Leftrightarrow m = {u^3} - 3u\) với \(u \in [ - 1;1]\).

 Xét hàm số \(f(u) = {u^3} - 3u\) với \(u \in [ - 1;1]\).

Lập BBT ta thấy phương trình có nghiệm khi và chỉ khi \( - 2 \le m \le 2\), mà \(m \in \mathbb{Z}\) nên \(m \in \{ 0; \pm 1; \pm 2\} \).

Câu 1: (YÊN PHONG 2019) Cho hàm số y=f(x). Biết rằng đồ thị hàm \(y = {f^\prime }(x)\) được cho như hình vẽ bên. Cho bất phương trình \(3f(x) \ge {x^3} - 3x + m\) (trong đó m là tham số thực). Hãy cho biết điều kiện cần và đủ để bất phương trình \(3f(x) \ge {x^3} - 3x + m\) đúng với \(\forall x \in [ - \sqrt 3 ;\sqrt 3 ]\) là ?

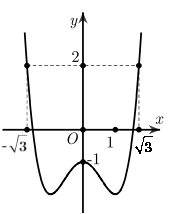
A. \(m \ge 3f( - \sqrt 3 )\)

B. \(m \le 3f(\sqrt 3 )\)

C. \(m \ge 3f(1)\)

D. \(m \le 3f(0)\)

Lời giải

 Ta có \(m \le 3f(x) - {x^3} + 3x \Leftrightarrow m \le {\min _{[ - \sqrt 3 ;\sqrt 3 ]}}\left( {3f(x) - {x^3} + 3x} \right)\).

Đặt \(g(x) = 3f(x) - {x^3} + 3x \Rightarrow {g^\prime }(x) = 3\left( {{f^\prime }(x) - {x^2} + 1} \right)\).

Vẽ đồ thị hàm số \(y = {x^2} - 1\) như hình vẽ bên.

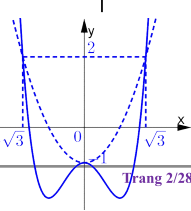
Từ đây ta tiết lập được bảng biến thiên như sau :

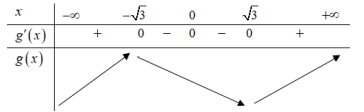
Từ bảng biến thiên ta suy ra rằng:

\(\begin{array}{l}m \le {\min _{[ - \sqrt 3 ;\sqrt 3 ]}}\left( {3f(x) - {x^3} + 3x} \right)\\ \Leftrightarrow m \le {\min _{[ - \sqrt 3 ;\sqrt 3 ]}}g(x) = g(\sqrt 3 ) = 3f(\sqrt 3 )\end{array}\).

Câu 2: (YÊN PHONG 2019) Biết đồ thị hàm số \(y = {x^2} - 3x + \frac{m}{x} + 3(m\) là tham số) có ba điểm cực trị. Parabol \(y = a{x^2} + bx + c\) đi qua ba điểm cực trị đó. Tính \(a + 2b + 4c\).

A. \(a + 2b + 4c = 0\)

B. \(a + 2b + 4c = 3\)

C. \(a + 2b + 4c =  - 4\)

D. \(a + 2b + 4c = 1\)

Lời giải

 Ta sử dụng tư duy hàm phân thức \(y = \frac{u}{v}\) có điểm cực trị thỏa mãn \(y = \frac{{{u^\prime }}}{{{v^\prime }}}\).

Ta suy ra \(y = \frac{{{x^3} - 3{x^2} + 3x + m}}{x}\) có các điểm cực trị nằm trên \(y = \frac{{{{\left( {{x^3} - 3{x^2} + 3x + m} \right)}^\prime }}}{{{{(x)}^\prime }}} = 3{x^2} - 6x + 3\).

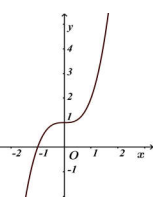
Câu 1. (Chuyên Quang Trung Bình Phước 2019) Cho hàm số y = f(x) liên tục trên \(\mathbb{R}\) có đồ thị như hình vẽ. Có bao nhiêu giá trị nguyên của n đề phương trình \(f\left( {16{{\cos }^2}x + 6\sin 2x - 8} \right) = f(n(n + 1))\) có nghiệm \(x \in \mathbb{R}\) ?

A. 10

B. 4

C. 8

D. 6

Lời giải

Ta có \(f\left( {16{{\cos }^2}x + 6\sin 2x - 8} \right) = f(n(n + 1))\) có nghiệm \(x \in \mathbb{R}\)

\( \Leftrightarrow 16{\cos ^2}x + 6\sin 2x - 8 = n(n + 1)\) có nghiệm \(x \in \mathbb{R}\)

\( \Leftrightarrow 8\cos 2{\rm{x}} + 6\sin 2{\rm{x}} = n(n + 1)\) có nghiệm \(x \in \mathbb{R}\)

Áp dụng bất đẳng thức Cauchy - Schwars: \({(8\cos 2x + 6\sin 2x)^2} \ge \left( {{8^2} + {6^2}} \right)\left( {{{\sin }^2}2x + {{\cos }^2}2x} \right) = 100\)

\(\begin{array}{l} \Leftrightarrow  - 10 \le 8\cos 2{\rm{x}} + 6\sin 2{\rm{x}} \le 10\\ \Rightarrow  - 10 \le n(n + 1) \le 10\\ \Leftrightarrow \frac{{ - 1 - \sqrt {41} }}{2} \le n \le \frac{{ - 1 + \sqrt {41} }}{2}\end{array}\)

\( \Rightarrow n \in \{  - 3; - 2; - 1;0;1;2\} \). Chọn D

Câu 2. (Chuyên Quang Trung - Bình Phước 2019). Có tất cả bao nhiêu giá trị nguyên âm của tham số m (biết \(m \ge  - 2019\) ) để hệ phương trình sau có nghiệm thực?

\(\left\{ {\begin{array}{*{20}{l}}{{x^2} + x - \sqrt[3]{y} = 1 - 2m(1)}\\{2{x^3} - {x^2}\sqrt[3]{y} - 2{x^2} + x\sqrt[3]{y} = m(2)}\end{array}} \right.\)

A. 2021

B. 2019

C. 2020

D. 2018

Lời giải

Hệ phương trình \( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{\left( {{x^2} - x} \right) + (2x - \sqrt[3]{y}) = 1 - 2m}\\{\left( {{x^2} - x} \right)(2x - \sqrt[3]{y}) = m}\end{array}} \right.\)

Đặt \(\left\{ {\begin{array}{*{20}{l}}{u = {x^2} - x}\\{v = 2x - \sqrt[3]{y}}\end{array}} \right.\). Khi đó u, v là 2 nghiệm của phương trình \({X^2} - (1 - 2m)X + m = 0(*)\).

Do đó để hệ phương trình có nghiệm thì

\(\begin{array}{l}{\Delta _{(*)}} \ge 0 \Leftrightarrow {(1 - 2m)^2} - 4m \ge 0\\ \Leftrightarrow 4{m^2} - 8m + 1 \ge 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{m \ge \frac{{2 + \sqrt 3 }}{2}}\\{m \le \frac{{2 - \sqrt 3 }}{2}}\end{array}} \right.{\rm{. }}\end{array}\)

Vì \(\left\{ {\begin{array}{*{20}{l}}{ - 2019 \le m < 0}\\{m \in \mathbb{Z}}\end{array} \Rightarrow m \in \{  - 2019; \ldots ; - 1\} } \right.\). Chọn C.

Câu 3. (Sổ GD\&ĐT Bạc Liêu 2019) Tìm m để giá trị lớn nhât của hàm số \(y = \left| {\sqrt {2x - {x^2}}  - 3m + 4} \right|\) đạt giá trị nhỏ nhất.

A. \(m = \frac{3}{2}\)

B. \(m = \frac{5}{3}\)

C. \(m = \frac{4}{3}\)

D. \(m = \frac{1}{2}\)

Lời giải

Ta có: xét \(g(x) = \sqrt {2x - {x^2}} \) có \({g^\prime }(x) = \frac{{1 - x}}{{\sqrt {2x - {x^2}} }}\) với \(x \in [0;2]\) nên \(\left\{ {\begin{array}{*{20}{l}}{{\mathop{\rm maxg}\nolimits} (x) = 1}\\{\min g(x) = 0}\end{array}} \right.\)

Ta có \(f(x) = |g(x) - 3m + 4|\) nên \(\max f(x) = \max \{ | - 3m + 4|;| - 3m + 5|\}  \ge \frac{{| - 3m + 4| + |3m - 5|}}{2} \ge \frac{1}{2}\)

Dấu bằng xảy ra \( \Leftrightarrow  - 3m + 4 = 3m - 5 \Rightarrow m = \frac{3}{2}\). Chọn \({\bf{A}}\)

Câu 4. (Chuyên Vinh 2019) Có bao nhiêu giá trị thực âm của m để phương trình \(\sqrt {m + \sqrt {m + {x^2}} }  = {x^2}\) có đúng 2 nghiệm thực?

A. 1 .

B. 3 .

C. Vô số.

D. 2 .

Lời giải

Điều kiện \[\left\{ {\begin{array}{*{20}{l}}{m + {x^2} \ge 0}\\{m + \sqrt {m + {x^2}}  \ge 0}\end{array}} \right.\]. Ta có:

\(\begin{array}{l}(*)\sqrt {m + \sqrt {m + {x^2}} }  = {x^2}\\ \Rightarrow {x^8} - 2m{x^4} - {x^2} + {m^2} - m = 0\\ \Leftrightarrow \left( { - {x^4} + {x^2} + m} \right)\left( { - {x^4} - {x^2} + m - 1} \right) = 0(m < 0)\end{array}\)

 \( \Leftrightarrow  - {x^4} + {x^2} + m = 0.\)

Đặt \(t = {x^2}(t \ge 0): - {t^2} + t + m = 0(1) \Rightarrow \) phương trình \((*)\) có đúng 2 nghiệm thực \( \Leftrightarrow \) phương trình (1) có 1 nghiệm dương duy nhất \( \Leftrightarrow m =  - \frac{1}{4} \Rightarrow \left[ {\begin{array}{*{20}{l}}{x = \frac{1}{{\sqrt 2 }}}\\{x =  - \frac{1}{{\sqrt 2 }}}\end{array}} \right.\) (TMĐK).

 Chọn A.

Câu 5. (Chuyên Vinh 2019) Xét đồ thị ( C) của hàm số \(y = {x^3} + 3ax + b\) với a, b là các số thực. Gọi M, N là hai điểm phân biệt thuộc (C ) sao cho tiếp tuyến với ( C) tại hai điểm có hệ số góc bằng 3. Biết khoảng cách từ gốc tọa độ tới đường thẳng M N bằng 1 , giá trị nhỏ nhất của \({a^2} + {b^2}\) là:

A. \(\frac{6}{5}\)

B. \(\frac{4}{3}\)

C. \(\frac{3}{2}\)

D. \(\frac{7}{6}\)

Lời giải

Ta có: tìm mối liên hệ giữa \({x_M}\) và \({y_M}\) bằng cách chia y cho \({y^\prime }\), ta được thương là \(\frac{x}{3}\), phần dư là \(2ax + b\), ta viết: \(y = \frac{x}{3} \cdot {y^\prime } + 2ax + b \Rightarrow {y_M} = \frac{{{x_M}}}{3} \cdot 3 + 2a{x_M} + b\) nên đường thẳng M N có dạng \(y = (2a + 1)x + b\)

\(\begin{array}{l} \Rightarrow {d_{(o,MN)}} = \frac{{|b|}}{{\sqrt {{{(2a + 1)}^2} + 1} }} = 1\\ \Rightarrow {b^2} = 4{a^2} + 4a + 2\\ \Rightarrow P = {a^2} + {b^2} = 5{a^2} + 4a + 2 \ge \frac{6}{5}.\end{array}\)

Chọn \({\bf{A}}\)

Câu 6. (Chuyên Vinh 2019) Cho các số thực x, y thỏa mãn \({x^2} + 2xy + 3{y^2} = 4\). Tìm giá trị lớn nhất của biểu thức \(P = {(x - y)^2}\)

A. \(\max P = 16\)

B. \(\max P = 12\)

C. \(\max P = 4\)

D. \(\max P = 8\)

Lời giải

Ta có:

\(\begin{array}{l}\left( {{x^2} + 2xy + 3{y^2}} \right)P = 4{(x - y)^2}\\ \Rightarrow {x^2}(4 - P) - 2xy(4 + P) + {y^2}(4 - 3P) = 0\end{array}\)

Do \(y \ne 0\) nên chia cả 2 vế cho \({y^2}\) và đặt \({\left( {\frac{x}{y}} \right)^2} = t\) ta được: \({t^2}(4 - P) - 2(4 + P) \cdot t + (4 - 3P) = 0\)

Để tồn tại

\(\begin{array}{l}t \Leftrightarrow {\Delta ^\prime } \ge 0\\ \Leftrightarrow {(4 + P)^2} - (4 - 3P)(4 - P) \ge 0\\ \Leftrightarrow P(12 - P) \ge 0 \Leftrightarrow P \le 12\end{array}\)

Chọn \({\bf{B}}\)

Chọn B

Câu 7. (Thuận Thành - Bắc Ninh 2019). Cho các số thực x, y, z thoả mãn điều kiện \(\left\{ {\begin{array}{*{20}{l}}{x - y + z = 3}\\{{x^2} + {y^2} + {z^2} = 5}\end{array}} \right.\). Hỏi biểu thức \(P = \frac{{x + y - 2}}{{z + 2}}\) có thể nhận bao nhiêu giá trị nguyên ?

A. 3 .

B. 1 .

C. 4 .

D. 2 .

Lời giải

 Ta có

\(\begin{array}{l}{x^2} + {y^2} + {z^2} = 5 \Leftrightarrow 5 - {z^2} = {x^2} + {y^2}\\ \Leftrightarrow 5 - {z^2} = \frac{{{{(x + y)}^2} + {{(x - y)}^2}}}{2}\end{array}\).

Lại có \(x - y + z = 3 \Leftrightarrow x - y = 3 - z\). Do đó \(5 - {z^2} = \frac{{{{(x + y)}^2} + {{(3 - z)}^2}}}{2} \Leftrightarrow {(x + y)^2} =  - 3{z^2} + 6z + 1\).

Khi đó

\(\begin{array}{l}P = \frac{{x + y - 2}}{{z + 2}}\\ \Leftrightarrow (z + 2)P + 2 = x + y\end{array}\)

 với \(z \ne  - 2\)

\(\begin{array}{l} \Leftrightarrow {(x + y)^2} = {[(z + 2)P + 2]^2}\\ \Leftrightarrow {(zP + 2P + 2)^2} =  - 3{z^2} + 6z + 1\\ \Leftrightarrow \left( {{P^2} + 3} \right){z^2} + 2\left( {2{P^2} + 2P - 3} \right)z + 4{P^2} + 8P + 3 = 0(1)\end{array}\)

Phương trình (1) có nghiệm khi và chỉ khi\(\begin{array}{l}{\Delta ^\prime } = {\left( {2{P^2} + 2P - 3} \right)^2} - \left( {{P^2} + 3} \right)\left( {4{P^2} + 8P + 3} \right) \ge 0\\ \Leftrightarrow 23{P^2} + 36P \le 0\\ \Leftrightarrow  - \frac{{36}}{{23}} \le P \le 0.\end{array}\)

Do \(z \in \mathbb{Z} \Rightarrow z \in \{  - 1;0\} \). Chọn D.

Câu 1: (Sơn Tây Hà Nội 2019) Cho hàm số \(y = {x^3} + 1\) có đồ thi (C ). Trên đường thẳng \(d:y = x + 1\) tìm được hai điểm \({M_1}\left( {{x_1};{y_1}} \right),{M_2}\left( {{x_2};{y_2}} \right)\) mà từ mỗi điểm đó kẻ được đúng hai tiếp tuyến đến (C ). Tính giá trị của biểu thức\(S = \frac{3}{5}\left( {{y_1}^2 + {y_2}^2 + {y_1}{y_2}} \right) + \frac{1}{3}\)

A. \(\frac{{113}}{{15}}\)

B. \(\frac{{41}}{{15}}\)

C. \(\frac{{14}}{{15}}\)

D. \(\frac{{59}}{{15}}\)

Lời giải: Ta có: Gọi \(\left( {{x_0};{y_0}} \right)\) là tiếp điểm ta sẽ có phương trinh tiếp tuyền qua điểm \({M_1}\) lả \(y = 3x_0^2\left( {x - {x_0}} \right) + x_0^3 + 1\). Thay \({M_1}\) vảo ta có: \({y_1} = 3x_0^2\left( {{x_1} - {x_0}} \right) + x_0^3 + 1\) mả \({y_1} = {x_1} + 1\) nên \({x_1} = 3{x_0}^2\left( {{x_1} - {x_0}} \right) + x_0^3 \Rightarrow {x_1} = \frac{{2{x_0}^3}}{{3{x_0}^2 - 1}}\), Yêu cầu bài toán \( \Leftrightarrow \) tìm m để sao cho \(m = \frac{{2{x^3}}}{{3{x^2} - 1}}\) có 2 nghiệm duy nhất \( \Leftrightarrow y = m\) cắt \(y = g(x) = \frac{{2{x^3}}}{{3{x^2} - 1}}\) tại 2 điểm phân biệt. Xét \({g^\prime }(x) = \frac{{6{x^2}\left( {{x^2} - 1} \right)}}{{{{\left( {3{x^2} - 1} \right)}^2}}} = 0 \Leftrightarrow x =  \pm 1\)

Ta có bảng biến thiên:

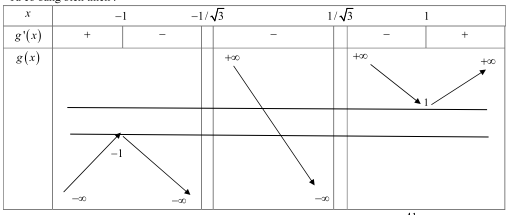
Dựa vào BBT ta xác định được \(m =  \pm 1\) nên \({x_{1,2}} =  \pm 1 \Rightarrow {y_1} = 2,{y_2} = 0\) thay vào \(S = \frac{{41}}{{15}}\). Chọn B