Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu Tổng hợp câu hỏi Vận dụng cao Hàm số ôn thi THPTQG năm 2021 có lời giải chi tiết, tài liệu bao gồm 87 trang. Tài liệu được tổng hợp từ các tài liệu ôn thi hay nhất  giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kỳ thi sắp hới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây

Tổng hợp câu hỏi Vận dụng cao Hàm số ôn thi THPTQG năm 2021 có lời giải chi tiết

CHƯƠNG I: HÀM SÓ VÀ CÁC BÀI TOÁN LIÊN QUAN

Chủ đề 1: Tính đơn điệu của hàm số

Ví dụ 1: Cho hàm số \[f(x)\]liên tục, không âm trên đoạn \[\left[ {0;\frac{\pi }{2}} \right]\], thỏa mãn \[f(0) = \sqrt 3 \] và \[f(x).f'(x) = \cos x\sqrt {1 + {f^2}(x)} ,\forall x \in \left[ {0;\frac{\pi }{2}} \right]\]. Tìm giá trị nhỏ nhất m và giá trị lớn nhất M của hàm số trên đoạn \[\left[ {\frac{\pi }{6};\frac{\pi }{2}} \right]\].

A. \[m = \frac{{\sqrt {21} }}{2},M = 2\sqrt 2 \].

B. \[m = \frac{5}{2},M = 3\].

C. \[m = \frac{{\sqrt 5 }}{2},M = \sqrt 3 \].

D. \[m = \sqrt 3 ,M = 2\sqrt 2 \].

Lời giải

Chọn A

Từ giả thiết \[f(x).f'(x) = \cos x\sqrt {1 + {f^2}(x)} \]

\[ \Rightarrow \frac{{f(x).f'(x)}}{{\sqrt {1 + {f^2}(x)} }} = \cos x \Rightarrow \int {\frac{{f(x).f'(x)}}{{\sqrt {1 + {f^2}(x)} }}dx = \sin x + C} \]

Đặt \[t = \sqrt {1 + {f^2}(x)}  \Rightarrow {t^2} = 1 + {f^2}(x) \Rightarrow tdt = f(x).f'(x)dx\].

Thay vào ta được \[\int {dt = \sin x + C \Rightarrow t = \sin x + C} \]

\[ \Rightarrow \sqrt {1 + {f^2}(x)}  = \sin x + C.\]

Do \[f(0) = \sqrt 3  \Rightarrow C = 2\]. Vậy \[\sqrt {1 + {f^2}(x)}  = \sin x + 2.\]

 \[ \Rightarrow {f^2}(x) = {\sin ^2}x + 4\sin x + 3\]

\[ \Rightarrow f(x) = \sqrt {{{\sin }^2}x + 4\sin x + 3} \], vì hàm số \[f(x)\]liên tục, không âm trên đoạn\[\left[ {0;\frac{\pi }{2}} \right]\].

Ta có \[\frac{\pi }{6} \le x \le \frac{\pi }{2} \Rightarrow \frac{1}{2} \le \sin x \le 1\], xét hàm số \[g(t) = {t^2} + 4t + 3\]có hoành độ đỉnh t = -2 loại.

Suy ra \[\mathop {\max }\limits_{\left[ {\frac{1}{2};1} \right]} g(t) = g(1) = 8,\mathop {\min }\limits_{\left[ {\frac{1}{2};1} \right]} g(t) = g\left( {\frac{1}{2}} \right) = \frac{{21}}{4}.\]

Suy ra \[\mathop {\max }\limits_{\left[ {\frac{\pi }{6};\frac{\pi }{2}} \right]} f(x) = f\left( {\frac{\pi }{2}} \right) = 2\sqrt 2 ,\mathop {\min }\limits_{\left[ {\frac{\pi }{6};\frac{\pi }{2}} \right]} f(x) = g\left( {\frac{\pi }{6}} \right) = \frac{{\sqrt {21} }}{2}.\]

Ví dụ 2: Cho hàm số \[f(x) = a{x^3} + b{x^2} + cx + d\] với a, b, c, d là các hệ số thực và \[a \ne 0\]. Hàm số \[f(x)\]nghịch biến trên R khi và chỉ khi:

A. \[\left\{ {\begin{array}{*{20}{c}}{a < 0}\\{{b^2} \le 3ac}\end{array}} \right.\]

B. \[\left\{ {\begin{array}{*{20}{c}}{a < 0}\\{{b^2} < 3ac}\end{array}} \right.\]

C. \[\left\{ {\begin{array}{*{20}{c}}{a > 0}\\{{b^2} \ge 3ac}\end{array}} \right.\]

D. \[\left\{ {\begin{array}{*{20}{c}}{a > 0}\\{{b^2} < 3ac}\end{array}} \right.\]

Lời giải

Chọn A

Ta có: \[f'(x) = 3a{x^2} + 2bx + c\]có \[\Delta {'_{f'(x)}} = {b^2} - 3ac.\]

Hàm số \[f(x)\]nghịch biến trên R khi và chỉ khi

\[\left\{ {\begin{array}{*{20}{c}}{3a < 0}\\{\Delta {'_{f'(x)}} \le 0}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{a < 0}\\{{b^2} - 3ac \le 0}\end{array}} \right.} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{a < 0}\\{{b^2} \le 3ac}\end{array}} \right.\].

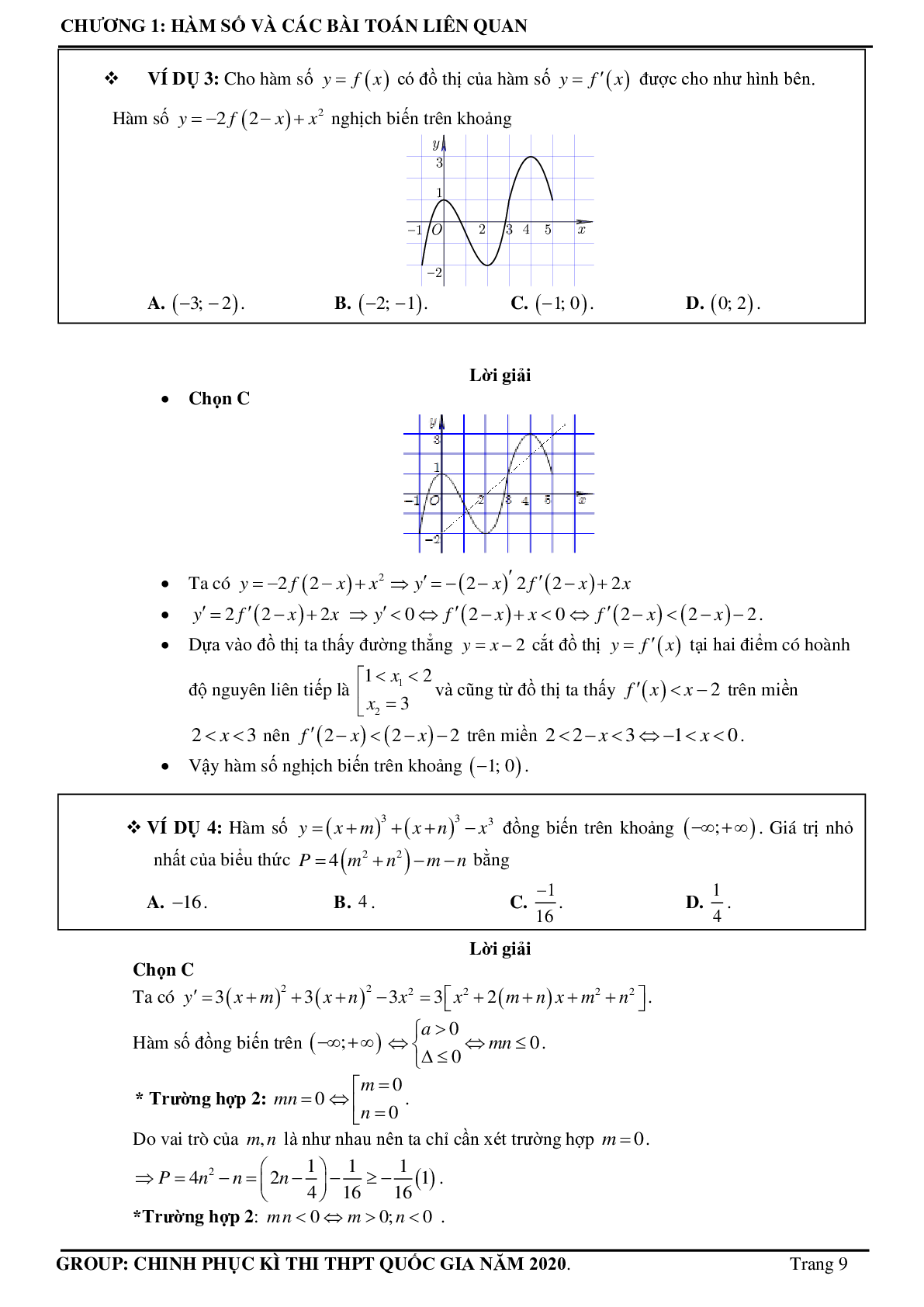
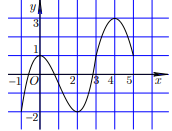
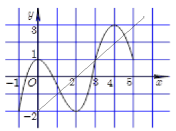
Ví dụ 3: Cho hàm số \[y = f(x)\] có đồ thị của hàm số \[y = f'(x)\] được cho như hình bên. Hàm số \[y =  - 2f(2 - x) + {x^2}\]nghịch biến trên khoảng

A. (-3 ;-2)

B. (-2;-1)

C. (-1;0)

D. (0;2)

 Lời giải

Chọn C

Ta có

\[\begin{array}{l}y =  - 2f(2 - x) + {x^2}\\ \Rightarrow y' =  - (2 - x)'2f'(2 - x) + 2x\end{array}\]

\[\begin{array}{l}y' = 2f'(2 - x) + 2x \Rightarrow y' < 0\\ \Leftrightarrow f'(2 - x) + x < 0\\ \Leftrightarrow f'(2 - x) < (2 - x) - 2\end{array}\].

Dựa vào đồ thị ta thấy đường thẳng \[y = x - 2\]cắt đồ thị \[y = f'(x)\]tại hai điểm có hoành độ nguyên liên tiếp là \[\left[ {\begin{array}{*{20}{c}}{1 < {x_1} < 2}\\{{x_2} = 3}\end{array}} \right.\]và cũng từ đồ thị ta thấy \[f'(x) < x - 2\]trên miền 2 < x < 3 nên \[f'(2 - x) < (2 - x) - 2\]trên miền 2 < 2 – x < 3 \[ \Leftrightarrow \]-1 < x < 0.

Vậy hàm số nghịch biến trên khoảng (-1;0).

Ví dụ 4: Hàm số \[y = {\left( {x + m} \right)^3} + {\left( {x + n} \right)^2} - {x^3}\]đồng biến trên khoảng \[\left( { - \infty ; + \infty } \right)\]. Giá trị nhỏ nhất của biểu thức \[P = 4\left( {{m^2} + {n^2}} \right) - m - n\] bằng

A. -16

B. 4

C. \[ - \frac{1}{{16}}\]

D. \[\frac{1}{4}\]

Lời giải

Chọn C

Ta có  \[y' = 3{\left( {x + m} \right)^2} + 2\left( {x + n} \right) - 3{x^2} = 3\left[ {{x^2} + 2(m + n)x + {m^2} + {n^2}} \right]\].

Hàm số đồng biến trên \[\left( { - \infty ; + \infty } \right)\]\[ \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{a > 0}\\{\Delta  \le 0}\end{array}} \right. \Leftrightarrow mn \le 0.\]

Trường hợp 2: \[mn = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{m = 0}\\{n = 0}\end{array}} \right.\].

Do vai trò của m, n là như nhau nên ta chỉ cần xét trường hợp m = 0.

\[ \Rightarrow P = 4{n^2} - n = \left( {2n - \frac{1}{4}} \right) - \frac{1}{{16}} \ge  - \frac{1}{{16}}\]  (1).

Trường hơp 2: \[mn < 0 \Leftrightarrow m > 0;n < 0\].

Ta có \[P = {\left( {2m - \frac{1}{4}} \right)^2} - \frac{1}{{16}} + 4{n^2} + ( - n) >  - \frac{1}{{16}}\]   (2).

Từ (1), (2) ta có \[{P_{\min }} =  - \frac{1}{{16}}\]. Dấu “=” xảy ra khi và chỉ khi \[m = \frac{1}{8};n = 0\]hoặc \[m = 0;n = \frac{1}{8}\].

Ví dụ 5: Tìm tập hợp tất cả các giá trị thực của tham số m để hàm số \[y = \frac{1}{3}{x^3} - (m + 1){x^2} + ({m^2} + 2m)x - 3\]nghịch biến trên khoảng (0;1).

A. \[[ - 1; + \infty )\]

B. \[( - \infty ;0]\]

C. \[[ - 1;0]\]

D. \[[0;1]\]

Lời giải

Chọn C

Ta có: \[y' = {x^2} - 2(m + 1)x + {m^2} + 2m;y' = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = m}\\{x = m + 2}\end{array}} \right.\]

Do đó ta có bảng biến thiên:

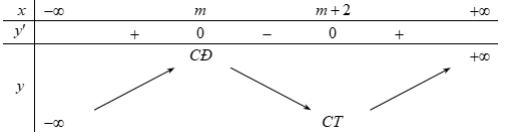
Để hàm số nghịch biến trên (0;1) thì \[(0;1) \subset (m;m + 2) \Rightarrow \left\{ {\begin{array}{*{20}{c}}{m \le 0}\\{m + 2 \ge 1}\end{array}} \right. \Leftrightarrow  - 1 \le m \le 0.\]

Bài tập rèn luyện

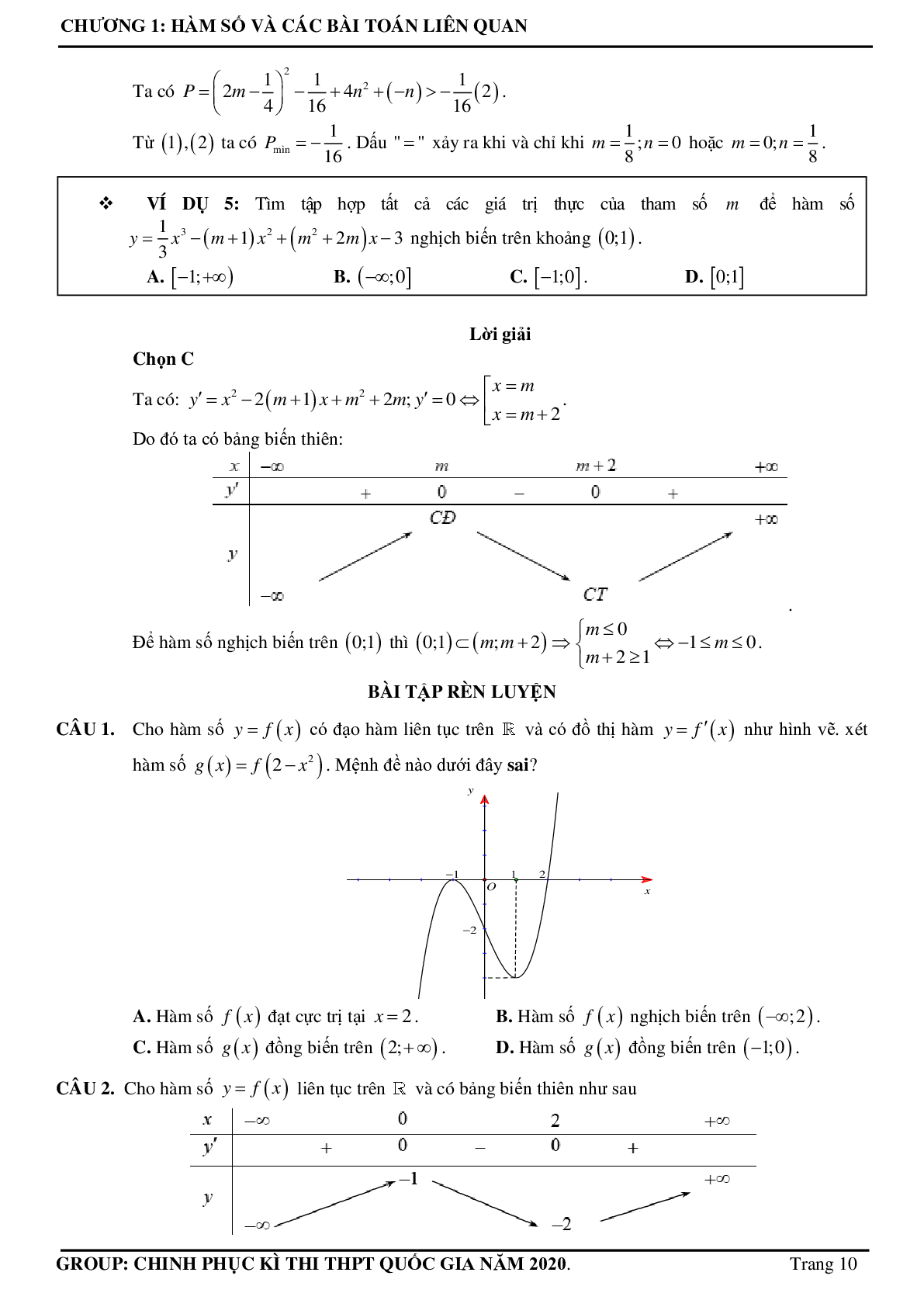
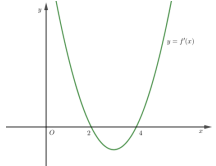
Câu 1. Cho hàm số \[y = f(x)\] có đạo hàm liên tục trên và có đồ thị hàm \[y = f'(x)\] như hình vẽ. xét hàm số \[g(x) = f\left( {2 - {x^2}} \right)\]. Mệnh đề nào dưới đây sai?

A. Hàm số \[f(x)\]đạt cực trị tại x = 2 .

B. Hàm số \[f(x)\]nghịch biến trên (-¥;2) .

C. Hàm số \[g(x)\] đồng biến trên (2;+¥) .

D. Hàm số \[g(x)\] đồng biến trên (-1;0) .

Câu 2. Cho hàm số \[y = f(x)\] liên tục trên và có bảng biến thiên như sau:

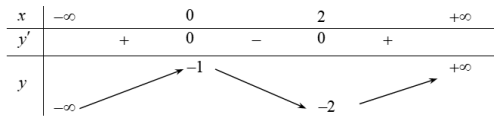
Có bao nhiêu mệnh đề đúng trong số các mệnh đề sau đối với hàm số \[g(x) = f\left( {2 - x} \right) - 2\]?

I. Hàm số \[g(x)\] đồng biến trên khoảng (-4;-2).

II. Hàm số \[g(x)\] nghịch biến trên khoảng (0;2).

III. Hàm số \[g(x)\] đạt cực tiểu tại điểm -2.

IV. Hàm số \[g(x)\] có giá trị cực đại bằng -3.

A. 3 .

B. 2 .

C. 1.

D. 4 .

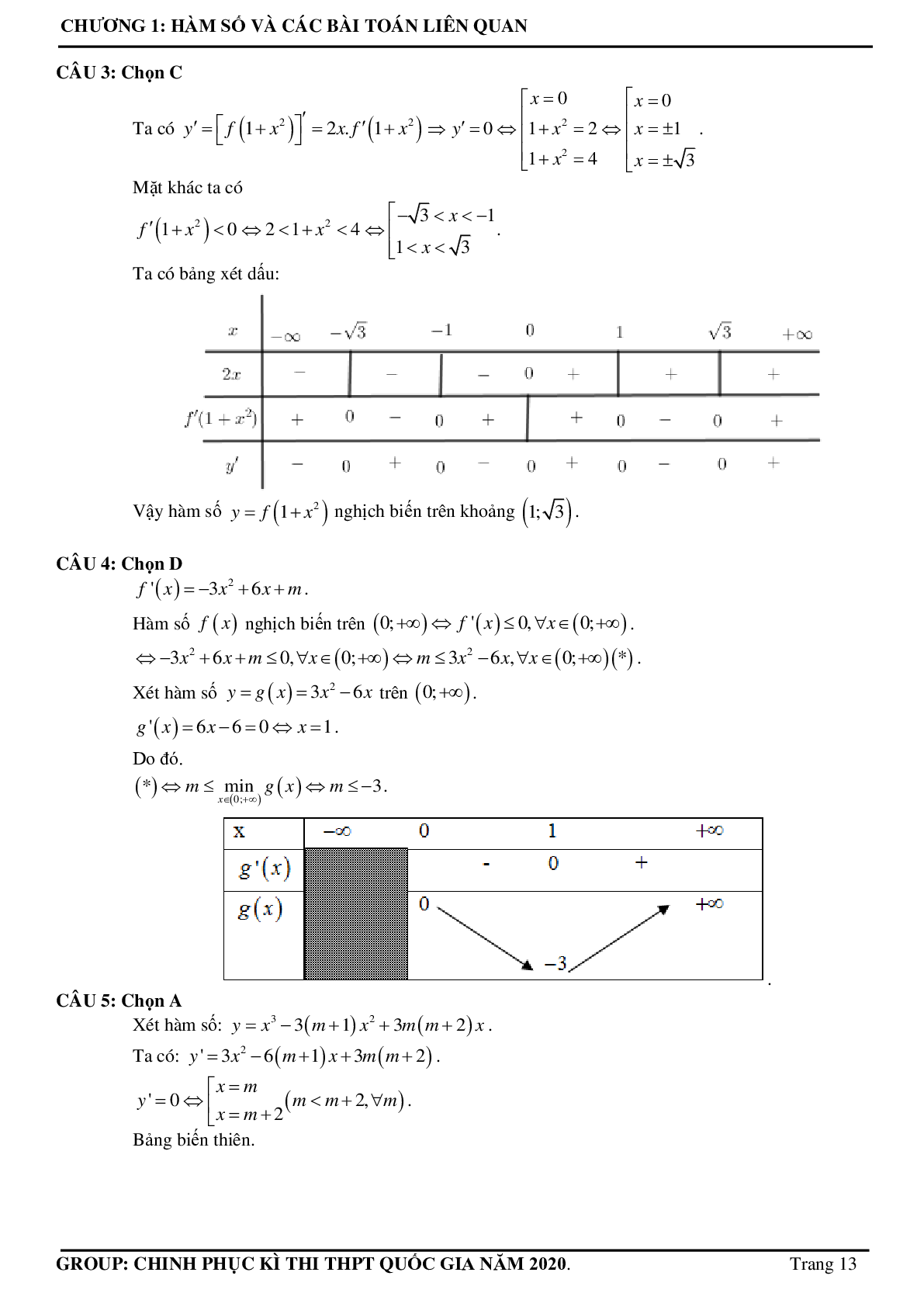
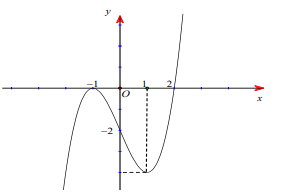
Câu 3: Cho hàm số \[y = f(x)\]. Hàm số \[y = f'(x)\] có đồ thị như hình vẽ bên. Hàm số \[y = f\left( {1 + {x^2}} \right)\] nghịch biến trên khoảng nào dưới đây?

A. (\[\sqrt 3 \];+¥).

B. (-\[\sqrt 3 \];-1).

C. (1; \[\sqrt 3 \]).

D. (0;1) .

Câu 4: Tìm tất cả các giá trị của tham số m để hàm số \[y =  - {x^3} + 3{x^2} + mx + 1\]nghịch biến trên khoảng (0;+¥).

A. m £ 0.

B. m ³-3.

C. m ³ 0.

D. m £-3.

Câu 5: Với tất cả các giá trị thực nào của tham số m thì hàm số \[y = {x^3} - 3(m + 1){x^2} + 3m(m + 2)x\] nghịch biến trên đoạn [0;1] ?

A. - 1 £ m £ 0.

B. - 1 < m < 0.

C. m ³ -1.

D. m £ 0.

Câu 6: Tìm m để hàm số \[y =  - {x^3} + 3{x^2} + 3mx + m - 1\] nghịch biến trên (0;+¥).

A. m > -1.

B. m £ -1.

C. m £ 1.

D. m < 1.

Câu 7: Có bao nhiêu giá trị nguyên âm của m để hàm số \[y = x + 5 + \frac{{1 - m}}{{x - 2}}\] đồng biến trên [5;+¥) ?

A. 10.

B. 8 .

C. 9 .

D. 11.

Câu 8: Tìm tập hợp tất cả các giá trị thực của tham số m để hàm số \[y = mx + (m + 1)\sqrt {x - 2} \] nghịch biến trên D = [2;+¥).

A. m £ -1.

B. m ³ 0.

C. m <-1.

D. - 2 £ m £ 1.

Câu 9: Cho hàm số \[f(x)\] có đạo hàm trên và có đồ thị \[y = f'(x)\] như hình vẽ. Xét hàm số \[g(x) = f\left( {{x^2} - 2} \right)\]. Mệnh đề nào sau đây sai?

A. Hàm số \[g(x)\] nghịch biến trên (-1;0) .

B. Hàm số \[g(x)\] nghịch biến trên (-¥;-2).

C. Hàm số \[g(x)\] nghịch biến trên (0;2).

D. Hàm số \[g(x)\] đồng biến trên (2;+¥).

Câu 10: Có bao nhiêu giá trị nguyên của tham số m để phương trình: \[\sqrt {1 + 2\cos x}  + \sqrt {1 + 2\sin x}  = \frac{m}{2}\] có nghiệm thực.

A.3.

B. 5.

C. 4.

D. 2.

Giải chi tiết

Câu 1: Chọn D

Dễ thấy \[f'(x)\] đổi dấu từ - sang + khi qua x = 2 nên hàm số \[f(x)\] đạt cực tiểu tại x = 2 nên A. đúng

\[f'(x) \le 0,\forall x \in ( - \infty ;2)\] nên hàm số \[f(x)\]nghịch biến trên (-¥;2) . B. đúng

Ta có \[g'(x) =  - 2x.f'\left( {2 - {x^2}} \right)\], \[g'(x) = 0 \Rightarrow \left[ {\begin{array}{*{20}{c}}{x = 0}\\{2 - {x^2} =  - 1}\\{2 - {x^2} = 2}\end{array}} \right. \Rightarrow \left[ {\begin{array}{*{20}{c}}{x = 0}\\{x = \sqrt 3 }\\{x =  - \sqrt 3 }\end{array}} \right.\]

trong đó \[x =  \pm \sqrt 3 \] là nghiệm kép, x = 0 là nghiệm bội bậc 3 , do đó, \[g'(x)\] chỉ đổi dấu qua x = 0 .

Lại có, \[g'(1) =  - 2.f'(1) =  - 2.( - 4) = 8 > 0\]

Ta có BBT

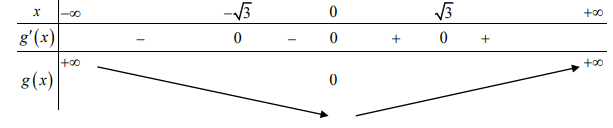
Từ BBT ta có hàm số đồng biến trên khoảng (0;+¥) và nghịch biến trên (-¥;0) . C. đúng, và D. sai.

Câu 2. Chọn C

Từ bảng biến thiên ta có hàm số \[y = f(x)\] có

\[f'(x) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = 0}\\{x = 2}\end{array},f'(x) > 0 \Leftrightarrow } \right.\left[ {\begin{array}{*{20}{c}}{x < 1}\\{x > 2}\end{array},} \right.\]

\[f'(x) < 0 \Leftrightarrow 0 < x < 2\]

và \[f(0) =  - 1,f(2) =  - 2\].

Xét hàm số \[g(x) = f(2 - x) - 2\] ta có \[g'(x) =  - f'(2 - x)\].

Giải phương trình \[g'(x) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{2 - x = 0}\\{2 - x = 2}\end{array}} \right.\].

Ta có

\[\begin{array}{l}g'(x) > 0 \Leftrightarrow  - f'(2 - x) > 0 \Leftrightarrow f'(2 - x) < 0\\ \Leftrightarrow 0 < 2 - x < 2 \Leftrightarrow 0 < x < 2.\end{array}\]

\[\begin{array}{l}g'(x) < 0 \Leftrightarrow  - f'(2 - x) < 0 \Leftrightarrow f'(2 - x) > 0\\ \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{2 - x < 0}\\{2 - x > 2}\end{array} \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x > 2}\\{x < 0}\end{array}.} \right.} \right.\end{array}\]

\[g(0) = f(2 - 0) - 2 = f(2) - 2 =  - 4\].

\[g(2) = f(2 - 2) - 2 = f(0) - 2 =  - 3\]

Bảng biến thiên

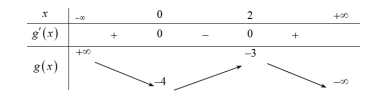
Từ bảng biến thiên ta có

Hàm số \[g(x)\] đồng biến trên khoảng (0;2) nên I sai.

Hàm số \[g(x)\] đồng biến trên khoảng (-¥;0) và (2;+¥) nên II sai.

Hàm số \[g(x)\] đạt cực tiểu tại x = 2 nên III sai.

Hàm số \[g(x)\] đạt cực đại tại x = 2 và nên IV đúng.