Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu Tóm tắt lý thuyết và bài tập trắc nghiệm về tính đơn điệu của hàm số, tài liệu bao gồm 17 trang. Tài liệu được tổng hợp từ các tài liệu ôn thi hay nhất  giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kỳ thi sắp hới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây

Tóm tắt lý thuyết và bài tập trắc nghiệm về tính đơn điệu của hàm số

CHỦ ĐỀ 1. TÍNH ĐƠN ĐIỆU CỦA HÀM SỐ

§ 1. Tính đơn điệu của hàm số

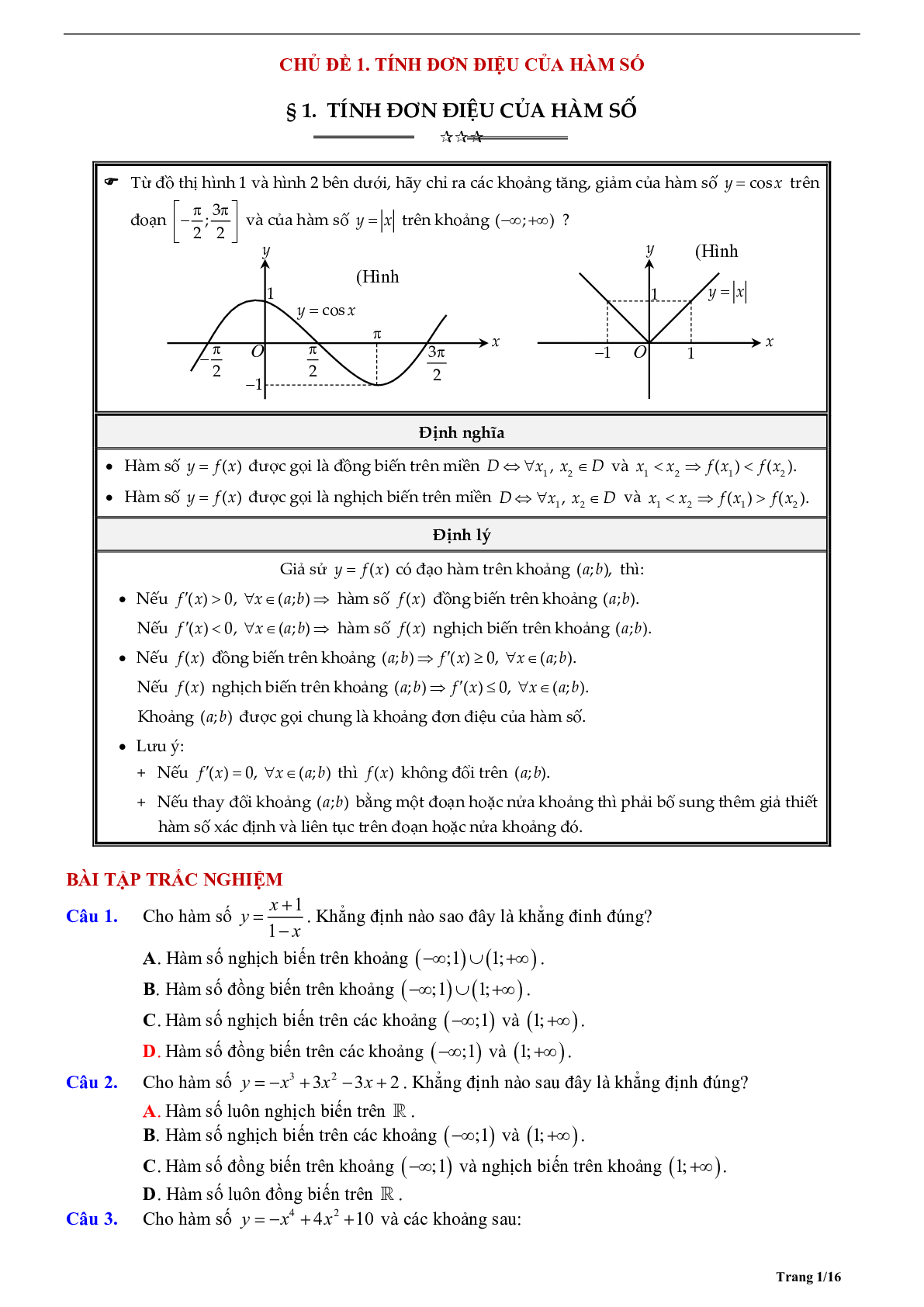
Từ đồ thị hình 1 và hình 2 bên dưới, hãy chỉ ra các khoảng tăng, giảm của hàm số \[y = \cos x\] trên đoạn \[\left[ { - \frac{\pi }{2};\frac{{3\pi }}{2}} \right]\] và của hàm số\[y = \left| x \right|\] trên khoảng (−∞;+∞) ?

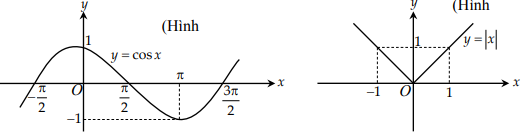
Định nghĩa

Hàm số \[y = f(x)\] được gọi là đồng biến trên miền \[D \Leftrightarrow \forall {x_1},{x_2} \in D\]và \[{x_1} < {x_2} \Rightarrow f({x_1}) < f({x_2})\].

Hàm số \[y = f(x)\] được gọi là nghịch biến trên miền \[D \Leftrightarrow \forall {x_1},{x_2} \in D\]và \[{x_1} < {x_2} \Rightarrow f({x_1}) > f({x_2})\].

Định lý

Giả sử \[y = f(x)\] có đạo hàm trên khoảng \[(a;b)\] thì:

Nếu \[f'(x) > 0,\forall x \in (a;b) \Rightarrow \]hàm số \[f(x)\] đồng biến trên khoảng \[(a;b)\]

Nếu \[f'(x) < 0,\forall x \in (a;b) \Rightarrow \]hàm số \[f(x)\] nghịch biến trên khoảng \[(a;b)\]

Nếu \[f(x)\] đồng biến trên khoảng \[(a;b)\]\[ \Rightarrow f'(x) \ge 0,\forall x \in (a;b).\]

Nếu \[f(x)\] nghịch biến trên khoảng \[(a;b)\]\[ \Rightarrow f'(x) \le 0,\forall x \in (a;b).\]

Khoảng\[(a;b)\] được gọi chung là khoảng đơn điệu của hàm số.

Lưu ý:

Nếu\[f'(x) = 0,\forall x \in (a;b)\]thì\[f(x)\]không đổi trên\[(a;b)\]

Nếu thay đổi khoảng\[(a;b)\]bằng một đoạn hoặc nửa khoảng thì phải bổ sung thêm giả thiết hàm số xác định và liên tục trên đoạn hoặc nửa khoảng đó.

Bài tập trắc nghiệm

Câu 1. Cho hàm số \[y = \frac{{x + 1}}{{1 - x}}\]. Khẳng định nào sao đây là khẳng đinh đúng?

A. Hàm số nghịch biến trên khoảng (−∞;1) ∪ (1;+∞).

B. Hàm số đồng biến trên khoảng (−∞;1) ∪ (1;+∞).

C. Hàm số nghịch biến trên các khoảng (−∞;1) và (1;+∞).

D. Hàm số đồng biến trên các khoảng (−∞;1) và (1;+∞).

Câu 2. Cho hàm số \[y =  - {x^3} + 3{x^2} - 3x + 2\]. Khẳng định nào sau đây là khẳng định đúng?

A. Hàm số luôn nghịch biến trên R.

B. Hàm số nghịch biến trên các khoảng (−∞;1) và (1;+∞).

C. Hàm số đồng biến trên khoảng (−∞;1) và nghịch biến trên khoảng (1;+∞).

D. Hàm số luôn đồng biến trên R.

Câu 3. Cho hàm số \[y =  - {x^4} + 4{x^2} + 10\] và các khoảng sau:

(I): (−∞;−\[\sqrt 2 \]) ; (II): (−\[\sqrt 2 \];0); (III): (0; \[\sqrt 2 \]);

Hỏi hàm số đồng biến trên các khoảng nào?

A. Chỉ (I).

B. (I) và (II).

C. (II) và (III).

D. (I) và (III).

Câu 4. Cho hàm số \[y = \frac{{3x - 1}}{{ - 4 + 2x}}\]. Khẳng định nào sau đây là khẳng định đúng?

A. Hàm số luôn nghịch biến trên R.

B. Hàm số luôn nghịch biến trên từng khoảng xác định.

C. Hàm số đồng biến trên các khoảng (−∞;2) và (2;+∞) .

D. Hàm số nghịch biến trên các khoảng (−∞; −2) và (−2;+∞).

Câu 5. Hỏi hàm số nào sau đây luôn nghịch biến trên R ?

A. \[h(x) = {x^4} - 4{x^2} + 4\].

B. \[g(x) = {x^3} + 3{x^2} + 10x + 1\].

C. \[f(x) =  - \frac{4}{5}{x^5} + \frac{4}{3}{x^3} - x\].

D. \[k(x) = {x^3} + 10x - {\cos ^2}x\].

Câu 6. Hỏi hàm số \[y = \frac{{{x^2} - 3x + 5}}{{x + 1}}\] nghịch biến trên các khoảng nào ?

A. (−∞;−4) và (2;+∞).

B. (−4;2) .

C. (−∞;−1) và (−1;+∞).

D. (−4;−1) và (−1;2) .

Câu 7. Hỏi hàm số \[y = \frac{{{x^3}}}{3} - 3{x^2} + 5x - 2\] nghịch biến trên khoảng nào?

A. (5;+∞)

B. (2;3)

C. (−∞;1)

D. (1;5)

Câu 8. Hỏi hàm số\[y = \frac{3}{5}{x^5} - 3{x^4} + 4{x^3} - 2\] đồng biến trên khoảng nào?

A. (−∞;0).

B. R.

C. (0;2).

D. (2;+∞).

Câu 9. Cho hàm số \[y = a{x^3} + b{x^2} + cx + d\]. Hỏi hàm số luôn đồng biến trên R khi nào?

A. \[\left[ {\begin{array}{*{20}{c}}{a = b = 0,c > 0}\\{a > 0;{b^2} - 3ac \le 0}\end{array}} \right.\].

B. \[\left[ {\begin{array}{*{20}{c}}{a = b = 0,c > 0}\\{a > 0;{b^2} - 3ac \ge 0}\end{array}} \right.\].

C. \[\left[ {\begin{array}{*{20}{c}}{a = b = 0,c > 0}\\{a < 0;{b^2} - 3ac \le 0}\end{array}} \right.\].

D. \[\left[ {\begin{array}{*{20}{c}}{a = b = c = 0}\\{a < 0;{b^2} - 3ac < 0}\end{array}} \right.\].

Câu 10. Cho hàm số \[y = {x^3} + 3{x^2} - 9x + 15\]. Khẳng định nào sau đây là khẳng định sai?

A. Hàm số nghịch biến trên khoảng (−3;1).

B. Hàm số đồng biến trên R.

C. Hàm số đồng biến trên (−9;−5).

D. Hàm số đồng biến trên khoảng (5;+∞).

Câu 11. Cho hàm số \[y = \sqrt {3{x^2} - {x^3}} \]. Khẳng định nào sau đây là khẳng định sai?

A. Hàm số đồng biến trên khoảng (0;2).

B. Hàm số đồng biến trên các khoảng (−∞;0); (2;3).

C. Hàm số nghịch biến trên các khoảng (−∞;0); (2;3).

D. Hàm số nghịch biến trên khoảng (2;3).

Câu 12. Cho hàm số \[y = \frac{x}{2} + {\sin ^2}x,x \in [0;\pi ]\]. Hỏi hàm số đồng biến trên các khoảng nào?

A. \[\left( {0;\frac{{7\pi }}{{12}}} \right)\]và \[\left( {\frac{{11\pi }}{{12}};\pi } \right)\].

B. \[\left( {\frac{{7\pi }}{{12}};\frac{{11\pi }}{{12}}} \right)\]

C. \[\left( {0;\frac{{7\pi }}{{12}}} \right)\]và \[\left( {\frac{{7\pi }}{{12}};\frac{{11\pi }}{{12}}} \right)\].

D. \[\left( {\frac{{7\pi }}{{12}};\frac{{11\pi }}{{12}}} \right)\] và \[\left( {\frac{{11\pi }}{{12}};\pi } \right)\].

Câu 13. Cho hàm số \[y = x + {\cos ^2}x\]. Khẳng định nào sau đây là khẳng định đúng?

A. Hàm số luôn đồng biến trên R.

B. Hàm số đồng biến trên \[\left( {\frac{\pi }{4} + k\pi ; + \infty } \right)\] và nghịch biến trên khoảng \[\left( { - \infty ;\frac{\pi }{4} + k\pi } \right)\].

C. Hàm số nghịch biến trên \[\left( {\frac{\pi }{4} + k\pi ; + \infty } \right)\]và đồng biến trên khoảng \[\left( { - \infty ;\frac{\pi }{4} + k\pi } \right)\].

D. Hàm số luôn nghịch biến trên R.

Câu 14. Cho các hàm số sau:

(I) : \[y = \frac{1}{3}{x^3} - {x^2} + 3x + 4\]

(II) : \[y = \frac{{x - 1}}{{x + 1}}\]

(III) : \[y = \sqrt {{x^2} + 4} \]

(IV) : \[y = {x^3} + 4x - \sin x\]

(V) : \[y = {x^4} + {x^2} + 2\]

Có bao nhiêu hàm số đồng biến trên những khoảng mà nó xác định?

A. 2.

B. 4.

C. 3.

D. 5.

Câu 15. Cho các hàm số sau:

(I) : \[y =  - {x^3} + 3{x^2} - 3x + 1\]

(II) : \[y = \sin x - 2x\]

(III) : \[y =  - \sqrt {{x^3} + 2} \]

(IV) : \[y = \frac{{x - 2}}{{1 - x}}\]

Hỏi hàm số nào nghịch biến trên toàn trục số?

A. (I), (II).

B. (I), (II) và (III).

C. (I), (II) và (IV).

D. (II), (III).

Câu 16. Xét các mệnh đề sau:

(I). Hàm số \[y =  - {(x - 1)^3}\] nghịch biến trên R.

(II). Hàm số \[y = \ln (x - 1) - \frac{x}{{x - 1}}\] đồng biến trên tập xác định của nó.

(III). Hàm số \[y = \frac{x}{{\sqrt {{x^2} + 1} }}\] đồng biến trên R.

Hỏi có bao nhiêu mệnh đề đúng?

A. 3.

B. 2.

C. 1.

D. 0.

Câu 17. Cho hàm số \[y = \left| {x + 1} \right|(x - 2)\]. Khẳng định nào sau đây là khẳng định sai?

A. Hàm số nghịch biến trên khoảng \[\left( { - 1;\frac{1}{2}} \right)\].

B. Hàm số nghịch biến trên khoảng \[\left( { - \infty ; - 1} \right)\].

C. Hàm số đồng biến trên các khoảng \[\left( { - \infty ; - 1} \right)\]và \[\left( {\frac{1}{2}; + \infty } \right)\].

D. Hàm số nghịch biến trên khoảng \[\left( { - 1;\frac{1}{2}} \right)\]và đồng biến trên khoảng \[\left( {\frac{1}{2}; + \infty } \right)\].

Câu 18. Cho hàm số \[y = x + 3 + 2\sqrt {2 - x} \]. Khẳng định nào sau đây là khẳng định đúng?

A. Hàm số nghịch biến trên khoảng (−∞;−2) và đồng biến trên khoảng (−2;2) .

B. Hàm số đồng biến trên khoảng (−∞;−2) và nghịch biến trên khoảng (−2;2) .

C. Hàm số đồng biến trên khoảng (−∞;1) và nghịch biến trên khoảng (1;2).

D. Hàm số nghịch biến trên khoảng (−∞;1) và đồng biến trên khoảng (1;2).

Câu 19. Cho hàm số \[y = \cos 2x + \sin 2x.\tan x,\forall x \in \left( { - \frac{\pi }{2};\frac{\pi }{2}} \right)\]. Khẳng định nào sau đây là khẳng định đúng?

A. Hàm số luôn giảm trên \[\left( { - \frac{\pi }{2};\frac{\pi }{2}} \right)\].

B. Hàm số luôn tăng trên \[\left( { - \frac{\pi }{2};\frac{\pi }{2}} \right)\].

C. Hàm số không đổi trên \[\left( { - \frac{\pi }{2};\frac{\pi }{2}} \right)\].

D. Hàm số luôn giảm trên \[\left( { - \frac{\pi }{2};0} \right)\].

Câu 20. Tìm tất cả các giá trị thực của tham số m sao cho hàm số \[y = \frac{{x - m + 2}}{{x + 1}}\] giảm trên các khoảng mà nó xác định ?

A. m < −3 .

B. m ≤ −3 .

C. m ≤1.

D. m < 1.

Câu 21. Tìm tất cả các giá trị thực của tham số m sao cho hàm số sau luôn nghịch biến trên R ? \[y =  - \frac{1}{3}{x^3} - m{x^2} + (2m - 3)x - m + 2\]

A. −3 ≤  m ≤ 1.

B. m ≤1.

C. −3 < m < 1.

D. m ≤−3 ; m ≥ 1.

Câu 22. Tìm tất cả các giá trị thực của tham số m sao cho hàm số \[y = \frac{{{x^2} - (m + 1) + 2m - 1}}{{x - m}}\] tăng trên từng khoảng xác định của nó?

A. m >1.

B. m ≤1.

C. m < 1.

D. m ≥ 1.

Câu 23. Tìm tất cả các giá trị thực của tham số m sao cho hàm số \[y = f(x) = x + m\cos x\] luôn đồng biến trên R ?

A. \[\left| m \right| \le 1\].

B. \[m > \frac{{\sqrt 3 }}{2}\].

C. \[\left| m \right| \ge 1\].

D. \[m < \frac{1}{2}\].

Câu 24. Tìm tất cả các giá trị thực của tham số m sao cho hàm số \[y = (m - 3)x - (2m + 1)\cos x\]luôn nghịch biến trên R ?

A. \[ - 4 \le m \le \frac{2}{3}\].

B. m ≥ 2 .

C. \[\left\{ {\begin{array}{*{20}{c}}{m > 3}\\{m \ne 1}\end{array}} \right.\].

D. m ≤ 2 .

Câu 25. Tìm tất cả các giá trị thực của tham số m sao cho hàm số sau luôn đồng biến trên R ? \[y = 2{x^3} - 3(m + 2){x^2} + 6(m + 1)x - 3m + 5\]

A. 0.

B. –1 .

C. 2.

D. 1.

Câu 26. Tìm giá trị nhỏ nhất của tham số m sao cho hàm số \[y = \frac{{{x^3}}}{3} + m{x^2} - mx - m\] luôn đồng biến trên R ?

A. m = −5 .

B. m = 0 .

C. m = −1 .

D. m = −6 .

Câu 27. Tìm số nguyên m nhỏ nhất sao cho hàm số \[y = \frac{{(m + 3)x - 2}}{{x + m}}\] luôn nghịch biến trên các khoảng xác định của nó?

A. m = −1 .

B. m = −2 .

C. m = 0 .

D. Không có m .

Câu 28. Tìm tất cả các giá trị thực của tham số m sao cho hàm số \[y = \frac{{mx + 4}}{{x + m}}\] giảm trên khoảng (−∞;1) ?

A. – 2 < m < 2.

B. – 2 ≤ m ≤ −1.

C. – 2 < m ≤− 1.

D. −2 ≤ m ≤  2.

Câu 29. Tìm tất cả các giá trị thực của tham số m sao cho hàm số \[y = {x^3} - 6{x^2} + mx + 1\] đồng biến trên khoảng (0;+∞) ?

A. m ≤ 0 .

B. m ≤ 12 .

C. m ≥ 0 .

D. m ≥ 12 .

Câu 30. Tìm tất cả các giá trị thực của tham số m sao cho hàm số \[y = {x^4} - 2(m - 1){x^2} + m - 2\] đồng biến trên khoảng (1;3) ?

A. m ∈ [−5;2).

B. m ∈ (−∞;2].

C. m ∈ (2;+∞) .

D. m ∈ (−∞;−5).

Câu 31. Tìm tất cả các giá trị thực của tham số m sao cho hàm số \[y = \frac{1}{3}{x^3} - \frac{1}{2}m{x^2} + 2mx - 3m + 4\] nghịch biến trên một đoạn có độ dài là 3?

A. m = −1; m = 9.

B. m = −1.

C. m = 9.

D. m = 1; m = −9 .

Câu 32. Tìm tất cả các giá trị thực của tham số m sao cho hàm số \[y = \frac{{\tan x - 2}}{{\tan x - m}}\] đồng biến trên khoảng \[\left( {0;\frac{\pi }{4}} \right)\]?

A. 1 ≤ m < 2.

B. m ≤ 0; 1 ≤ m < 2.

C. m ≥ 2 .

D. m ≤ 0 .

Câu 33. Tìm tất cả các giá trị thực của tham số m sao cho hàm số \[y = f(x) = \frac{{m{x^3}}}{3} + 7m{x^2} + 14x - m + 2\] giảm trên nửa khoảng [1;+∞) ?

A. \[\left( { - \infty ; - \frac{{14}}{{15}}} \right)\]

B. \[\left( { - \infty ; - \frac{{14}}{{15}}} \right]\]

C. \[\left[ { - 2; - \frac{{14}}{{15}}} \right]\]

D. \[\left[ { - \frac{{14}}{{15}}; + \infty } \right)\]

Câu 34. Tất cả các giá trị thực của tham số m sao cho hàm số \[y =  - {x^4} + (2m - 3){x^2} + m\]  nghịch biến trên khoảng (1;2) là \[\left( { - \infty ;\frac{p}{q}} \right]\], trong đó phân số \[\frac{p}{q}\] tối giản và q > 0 . Hỏi tổng p + q là?

A. 5.

B. 9.

C. 7.

D. 3.

Câu 35. Hỏi có bao nhiêu giá trị nguyên của tham số m sao cho hàm số \[y = \frac{{{x^2} - 2mx + m + 2}}{{x - m}}\] đồng biến trên từng khoảng xác định của nó?

A. Hai.

B. Bốn.

C. Vô số.

D. Không có.

Câu 36. Hỏi có bao nhiêu giá trị nguyên dương của tham số m sao cho hàm số \[y = \frac{{2{x^2} + (1 - m)x + 1 + m}}{{x - m}}\] đồng biến trên khoảng (1;+∞)?

A. 3.

B. 1.

C. 2.

D. 0.

Câu 37. Tìm tất cả các giá trị thực của tham số α và β sao cho hàm số \[y = f(x) = \frac{{ - {x^3}}}{3} + \frac{1}{2}(\sin \alpha  + \cos \alpha ){x^2} - \frac{3}{2}x\sin \alpha \cos \alpha  - \sqrt {\beta  - 2} \] luôn giảm trên R?

A. \[\frac{\pi }{{12}} + k\pi  \le \alpha  \le \frac{\pi }{4} + k\pi ,k \in Z\] và β ≥ 2 .

B. \[\frac{\pi }{{12}} + k\pi  \le \alpha  \le \frac{{5\pi }}{{12}} + k\pi ,k \in Z\]và β ≥ 2 .

C. \[\alpha  \le \frac{\pi }{{12}} + k\pi \], \[k \in Z\] và β ≥ 2 .

D. \[\alpha  \ge \frac{{5\pi }}{{12}} + k\pi ,k \in Z\] và β ≥ 2 .

Câu 38. Tìm mối liên hệ giữa các tham số a và b sao cho hàm số \[y = f(x) = 2x + a\sin x + b\cos x\] luôn tăng trên R ?

A. \[\frac{1}{a} + \frac{1}{b} = 1\].

B. \[a + 2b = 2\sqrt 3 \].

C. \[{a^2} + {b^2} \le 4\].

D. \[a + 2b \ge \frac{{1 + \sqrt 2 }}{3}\].