Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu Tóm tắt lý thuyết và bài tập trắc nghiệm về tương giao giữa hai đồ thị hàm số, tài liệu bao gồm 27 trang. Tài liệu được tổng hợp từ các tài liệu ôn thi hay nhất  giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kỳ thi sắp hới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây

Tóm tắt lý thuyết và bài tập trắc nghiệm về tương giao giữa hai đồ thị hàm số

CHỦ ĐỀ 6. SỰ TƯƠNG GIAO GIỮA HAI ĐỒ THỊ HÀM SỐ

I. Sự tương giao của đường thẳng và đồ thị hàm số bậc ba

1. KIẾN THỨC TRỌNG TÂM

Xét hàm số bậc ba \[y = a{x^3} + b{x^2} + cx + d\]  (a ≠ 0) có đồ thị (C) và hàm số bậc nhất \[y = kx + n\] có đồ thị d.

Lập phương trình hoành độ giao điểm của (C) và \[d:a{x^3} + b{x^2} + cx + d = kx + n\] (1) Phương trình (1) là phương trình bậc ba nên có ít nhất một nghiệm. Ta có 2 trường hợp:

Trường hợp 1: Phương trình (1) có “nghiệm đẹp” x₀.

Thường thì đề hay cho nghiệm x₀ = 0; ±1; ± 2; ... thì khi đó:

(1) \[ \Leftrightarrow \left( {x - {x_0}} \right)\left( {A{x^2} + Bx + C} \right) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x - {x_0} = 0}\\{A{x^2} + Bx + C(2)}\end{array}} \right.\]

Khi đó:

(C) và d có ba giao điểm⇔ phương trình (1) có ba nghiệm phân biệt ⇔ phương trình (2) có hai nghiệm phân biệt khác nghiệm x₀. (Đây là trường hợp thường gặp)

(C) và d có hai giao điểm⇔ phương trình (1) có hai nghiệm phân biệt ⇔ phương trình (2) có hai nghiệm phân biệt, trong đó có một nghiệm x₀ hoặc phương trình (2) có nghiệm kép khác x₀ .

(C) và d có một giao điểm⇔ phương trình (1) có một nghiệm⇔ phương trình (2) vô nghiệm hoặc phương trình (2) có nghiệm kép là x₀.

Trường hợp 2: Phương trình (1) không thể nhẩm được “nghiệm đẹp” thì ta biến đổi phương trình (1) sao cho hạng tử chứa x tất cả nằm bên vế trái, các hạng tử chứa tham số m nằm bên vế phải, nghĩa là (1) ⇔ \[f(x) = g(m)\].

Ta khảo sát và vẽ bảng biến thiên hàm số \[y = f(x)\] và biện luận số giao điểm của (C) và d theo tham số m .

2. Các ví dụ

Ví dụ 1: Tìm giao điểm của đồ thị (C): \[y = {x^3} - 3{x^2} + 2x + 1\] và đường thẳng y =1. Hướng dẫn giải

Phương trình hoành độ giao điểm:

\[\begin{array}{l}{x^3} - 3{x^2} + 2x + 1 = 1 \Leftrightarrow {x^3} - 3{x^2} + 2x = 0\\ \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = 0}\\{x = 1}\\{x = 2}\end{array}} \right.\end{array}\]

Vậy có ba giao điểm A (0;1), B (1;1), C (2;1).

Ví dụ 2: Cho hàm số \[y = m{x^3} - {x^2} - 2x + 8m\] có đồ thị là (C_m). Tìm m đồ thị (C_m) cắt trục hoành tại ba điểm phân biệt.

Hướng dẫn giải

Phương trình hoành độ giao điểm \[m{x^3} - {x^2} - 2x + 8m = 0\]  (1)

⇔ \[\begin{array}{l}\left( {x + 2} \right)\left[ {m{x^2} - (2m + 1)x + 4m} \right] = 0\\ \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x =  - 2}\\{m{x^2} - (2m + 1)x + 4m = 0(2)}\end{array}} \right.\end{array}\]

(C_m) cắt trục hoành tại ba điểm phân biệt ⇔ (1) có ba nghiệm phân biệt.

⇔ (2) có hai nghiệm phân biệt khác −2

⇔ \[\left\{ {\begin{array}{*{20}{c}}{m \ne 0}\\{\Delta  =  - 12{m^2} + 4m + 1 > 0}\\{12m + 2 \ne 0}\end{array}} \right.\]

⇔\[\left\{ {\begin{array}{*{20}{c}}{m \ne 0}\\{ - \frac{1}{6} < m < \frac{1}{6}}\\{m \ne  - \frac{1}{6}}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{m \ne 0}\\{ - \frac{1}{6} < m < \frac{1}{6}}\end{array}} \right.\].

Vậy \[m \in \left( { - \frac{1}{6};\frac{1}{2}} \right)\backslash \{ 0\} \] thỏa yêu cầu bài toán.

Ví dụ 3: Cho hàm số \[y = 2{x^3} - 3m{x^2} + (m - 1)x + 1\] có đồ thị (C). Tìm m để đường thẳng d: \[y =  - x + 1\] cắt đồ thị (C) tại ba điểm phân biệt.

Hướng dẫn giải

Phương trình hoành độ giao điểm của (C) và d :

\[\begin{array}{l}2{x^3} - 3m{x^2} + (m - 1)x + 1 =  - x + 1\\ \Leftrightarrow x\left( {2{x^2} - 3mx + m} \right) = 0\\ \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = 0}\\{2{x^2} - 3mx + m = 0(*)}\end{array}} \right.\end{array}\]

Yêu cầu bài toán ⇔ (*) có hai nghiệm phân biệt khác 0

\[ \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{\Delta  = 9{m^2} - 8m > 0}\\{m \ne 0}\end{array}} \right. \Leftrightarrow m \in \left( { - \infty ;0} \right) \cup \left( {\frac{8}{9}; + \infty } \right)\]

Vậy \[m \in \left( { - \infty ;0} \right) \cup \left( {\frac{8}{9}; + \infty } \right)\] thỏa yêu cầu bài toán.

Ví dụ 4: Tìm m để đồ thị hàm số \[y = {x^3} + mx + 2\] cắt trục hoành tại một điểm duy nhất.

Hướng dẫn giải

Phương trình hoành độ giao điểm của đồ thị hàm số với trục hoành là

\[{x^3} + mx + 2 = 0\].

Vì x = 0 không là nghiệm của phương trình, nên phương trình tương đương với

\[m =  - {x^2} - \frac{2}{x}\]     ( x ≠ 0)

Xét hàm số \[f(x) =  - {x^2} - \frac{2}{x}\] với x ≠ 0 , suy ra \[f'(x) =  - 2x + \frac{2}{{{x^2}}} = \frac{{ - 2{x^3} + 2}}{{{x^2}}}\].

Vậy \[f'(x) = 0 \Leftrightarrow x = 1\].

Bảng biến thiên:

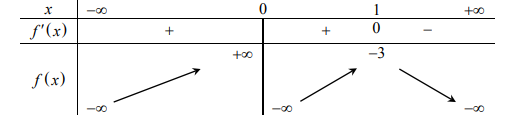
Dựa vào bảng biến thiên ta thấy đồ thị cắt trục hoành tại một điểm duy nhất ⇔ m > −3. Vậy m > −3 thỏa yêu cầu bài toán.

Ví dụ 5: Tìm m để đồ thị (C) của hàm số \[y = {x^3} - 3{x^2} - 9x + m\] cắt trục hoành tại ba điểm phân biệt.

Hướng dẫn giải

Phương trình hoành độ giao điểm của đồ thị và trục hoành:

\[{x^3} - 3{x^2} - 9x + m = 0 \Leftrightarrow {x^3} - 3{x^2} - 9x =  - m\]      (1)

Phương trình (1) là phương trình hoành độ giao điểm của đường (C): \[y = {x^3} - 3{x^2} - 9x\]và đường thẳng d: \[y =  - m\]. Số nghiệm của (1) bằng số giao điểm của (C) và d .

Khảo sát và vẽ bảng biến thiên của hàm số \[y = {x^3} - 3{x^2} - 9x\].

Tập xác định D = R.

Đạo hàm

\[\begin{array}{l}y' = 3{x^2} - 6x - 9;y' = 0\\ \Leftrightarrow 3{x^2} - 6x - 9 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = 3}\\{x =  - 1}\end{array}} \right.\end{array}\].

Bảng biến thiên:

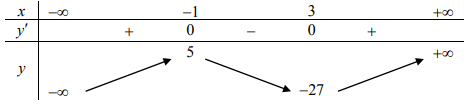
Dựa vào bảng biến thiên ta thấy (1) có ba nghiệm phân biệt

⇔−27 < −m < 5 ⇔ − 5 < m < 27.

Ví dụ 6: Gọi d là đường thẳng đi qua điểm A(−1;0) với hệ số góc k (k ∈ R). Tìm k để đường thẳng d cắt đồ thị hàm số (C): \[y = {x^3} - 3{x^2} + 4\] tại ba điểm phân biệt A, B, C và tam giác OBC có diện tích bằng 1 (O là gốc tọa độ).

Hướng dẫn giải

Đường thẳng d đi qua A(−1;0) và có hệ số góc k nên có dạng y = k (x + 1), hay

 kx – y + k = 0.

Phương trình hoành độ giao điểm của (C) và d là:

\[\begin{array}{l}{x^3} - 3{x^2} + 4 = kx + k \Leftrightarrow \left( {x + 1} \right)\left( {{x^2} - 4x + 4 - k} \right) = 0\\ \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x =  - 1}\\{g(x) = {x^2} - 4x + 4 - k(*)}\end{array}} \right.\end{array}\]

d cắt (C) tại ba điểm phân biệt⇔ phương trình (*) có hai nghiệm phân biệt khác −1

\[ \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{\Delta ' > 0}\\{g( - 1) \ne 0}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{k > 0}\\{k \ne 9}\end{array}} \right.\]

Khi đó \[g(x) = 0 \Leftrightarrow x = 2 - \sqrt k ;x = 2 + \sqrt k \]. Vậy các giao điểm của hai đồ thị lần lượt là \[A( - 1;0),B(2 - \sqrt k ;3k - k\sqrt k ),C(2 + \sqrt k ;3k + k\sqrt k )\].

Tính được \[BC = 2\sqrt k \sqrt {1 + {k^2}} ,d(O,BC) = d(O,d) = \frac{{\left| k \right|}}{{\sqrt {1 + {k^2}} }}\]. Khi đó

\[\begin{array}{l}{S_{\Delta OBC}} = \frac{1}{2}.\frac{{\left| k \right|}}{{\sqrt {1 + {k^2}} }}.2\sqrt k .\sqrt {1 + {k^2}}  = 1\\ \Leftrightarrow \left| k \right|\sqrt k  = 1 \Leftrightarrow {k^3} = 1 \Leftrightarrow k = 1\end{array}\].

Vậy k =1 thỏa yêu cầu bài toán.

II. Sự tương giao của đường thẳng với đồ thị hàm số trùng phương

1. Kiến thức trọng tâm

Cho hàm số \[y = a{x^4} + b{x^2} + c\]   (a ≠ 0) có đồ thị (C) và đường thẳng y = k có đồ thị d. Lập phương trình hoành độ giao điểm của (C) và d : \[a{x^4} + b{x^2} + c = k\]   (1)

Đặt \[t = {x^2}\]  ( t ≥ 0) ta có phương trình \[a{t^2} + bt + c - k = 0\]   (2)

(C) và d có bốn giao điểm ⇔ (1) có bốn nghiệm phân biệt ⇔ (2) có hai nghiệm dương phân biệt ⇔ phương trình (2) thỏa \[\left\{ {\begin{array}{*{20}{c}}{\Delta  > 0}\\{P > 0}\\{S > 0}\end{array}} \right.\]. (Trường hợp này thường gặp)

(C) và d có ba giao điểm ⇔ (1) có ba nghiệm phân biệt⇔ (2) có hai nghiệm phân biệt, trong đó có một nghiệm dương và một nghiệm t = 0 .

(C) và d có hai giao điểm ⇔ (1) có hai nghiệm phân biệt ⇔ (2) có nghiệm kép dương hoặc có hai nghiệm trái dấu.

(C) và d không có giao điểm⇔ (1) vô nghiệm⇔ (2) vô nghiệm hoặc chỉ có nghiệm âm.

(C) và d có một giao điểm⇔ (1) có một nghiệm⇔ (2) có nghiệm t = 0 và một nghiệm âm.

2. Các ví dụ

Ví dụ 1: Tìm giao điểm của đồ thị (C): \[y = {x^4} + 2{x^2} - 3\] và trục hoành.

Hướng dẫn giải

Phương trình hoành độ giao điểm:

 \[y = {x^4} + 2{x^2} - 3 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{{x^2} = 1}\\{{x^2} =  - 3}\end{array}} \right. \Rightarrow x = 1 \vee x =  - 1\].

Vậy có hai giao điểm: A (−1;0), B (1;0)

Ví dụ 2: Tìm m để phương trình \[y = {x^4} - 2{x^2} - m + 3 = 0\] có bốn nghiệm phân biệt.

Hướng dẫn giải

Phương trình: \[{x^4} - 2{x^2} - m + 3 = 0 \Leftrightarrow {x^4} - 2{x^2} + 3 = m\]   (1)

Phương trình (1) là phương trình hoành độ giao điểm của hai đường (C): \[y = {x^4} - 2{x^2} + 3\]và đường thẳng d: \[y = m\]. Số nghiệm của (1) bằng số giao điểm của (C) và d.

Khảo sát và vẽ bảng biến thiên của hàm số \[y = {x^4} - 2{x^2} + 3\].

Tập xác định D = R.

Đạo hàm

\[\begin{array}{l}y' = 4{x^3} - 4x;\\y' = 0 \Leftrightarrow 4{x^3} - 4x = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = 0}\\{x = 1}\\{x =  - 1}\end{array}} \right.\end{array}\].

Bảng biến thiên:

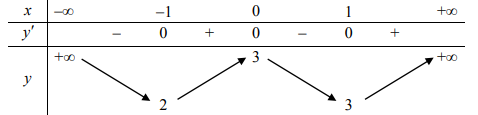
Dựa vào bảng biến thiên ta thấy (1) có bốn nghiệm phân biệt ⇔ 2 < m < 3.

Vậy 2 < m < 3 thỏa yêu cầu bài toán.

Ví dụ 3: Cho hàm số \[y = {x^4} - 2(m + 1){x^2} + {m^2} - 3m - 2\]  (C_m). Định m để đồ thị (C_m) cắt đường thẳng d:  y = −2 tại bốn điểm phân biệt.

Lời giải

Phương trình hoành độ giao điểm của (C_m) và d :

\[\begin{array}{l}{x^4} - 2(m + 1){x^2} + {m^2} - 3m - 2 =  - 2\\ \Leftrightarrow {x^4} - 2(m + 1){x^2} + {m^2} - 3m = 0\end{array}\]   (1)

Đặt \[t = {x^2}\]  ( t ≥ 0),  phương trình trở thành

\[{t^2} - 2(m + 1)t + {m^2} - 3m = 0\]   (2).

(C_m) và d có bốn giao điểm ⇔ (1) có bốn nghiệm phân biệt ⇔ (2) có hai nghiệm dương phân biệt.

\[\begin{array}{l}\left\{ {\begin{array}{*{20}{c}}{\Delta ' > 0}\\{P > 0}\\{S > 0}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{5m + 1 > 0}\\{{m^2} - 3m > 0}\\{2(m + 1) > 0}\end{array}} \right.\\ \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{m >  - \frac{1}{5}}\\{m < 0,m > 3}\\{m >  - 1}\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{ - \frac{1}{5} < m < 0}\\{m > 3}\end{array}} \right.\end{array}\]

Vậy \[m \in \left( { - \frac{1}{5};0} \right) \cup (3; + \infty )\] thỏa yêu cầu bài toán.

Ví dụ 4: Cho hàm số \[y = {x^4} - (3m + 2){x^2} + 3m\]  (C) . Tìm m để đường thẳng d: \[y =  - 1\] cắt đồ thị (C) tại bốn điểm phân biệt có hoành độ đều nhỏ hơn 2.

Hướng dẫn giải

Phương trình hoành độ giao điểm của (C) và d : y = −1 là

\[{x^4} - (3m + 2){x^2} + 3m =  - 1 \Leftrightarrow {x^4} - (3m + 2){x^2} + 3m + 1 = 0\]

Đặt \[t = {x^2}\]  ( t ≥ 0), ta có phương trình

\[{t^2} - (3m + 2)t + 3m + 1 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{t = 1}\\{t = 3m + 1}\end{array}} \right.\]

Khi đó \[\left[ {\begin{array}{*{20}{c}}{{x^2} = 1}\\{{x^2} = 3m + 1}\end{array}} \right.\]. Yêu cầu bài toán \[ \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{0 < 3m + 1 < 4}\\{3m + 1 \ne 1}\end{array}} \right. \Leftrightarrow  - \frac{1}{3} < m < 1\] và \[m \ne 0\]

Vậy \[ - \frac{1}{3} < m < 1\] và \[m \ne 0\]thỏa yêu cầu bài toán.

Ví dụ 5: Cho hàm số \[y = {x^4} - (3m + 4){x^2} + {m^2}\] có đồ thị là (C_m). Tìm m để đồ thị (C_m) cắt trục hoành tại bốn điểm phân biệt có hoành độ lập thành một cấp số cộng.

Hướng dẫn giải

Phương trình hoành độ giao điểm: \[{x^4} - (3m + 4){x^2} + {m^2} = 0\]  (1)

Đặt \[t = {x^2}\]  ( t ≥ 0), phương trình (1) trở thành: \[{t^2} - (3m + 4)t + {m^2}\] (2)

(C_m) cắt trục hoành tại bốn điểm phân biệt ⇔ (1) có bốn nghiệm phân biệt ⇔

(2) có hai nghiệm dương phân biệt ⇔ \[\left\{ {\begin{array}{*{20}{c}}{\Delta  = 5{m^2} + 24m + 16 > 0}\\{P = {m^2} > 0}\\{S = 3m + 4 > 0}\end{array}} \right.\]

⇔ \[\left\{ {\begin{array}{*{20}{c}}{m <  - 4 \vee m >  - \frac{4}{5}}\\{m \ne 0}\\{m >  - \frac{4}{5}}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{m >  - \frac{4}{5}}\\{m \ne 0}\end{array}} \right.\] (*)

Khi đó phương trình (2) có hai nghiệm 0 < t₁ < t₂. Suy ra phương trình (1) có bốn nghiệm phân biệt là \[{x_1} =  - \sqrt {{t_2}}  < {x_2} =  - \sqrt {{t_1}}  < {x_3} = \sqrt {{t_1}}  < {x_4} = \sqrt {{t_2}} \]. Bốn nghiệm x₁, x₂, x₃, x₄ lập thành cấp số cộng

\[\begin{array}{l}{x_2} - {x_1} = {x_3} - {x_2} = {x_4} - {x_3}\\ \Leftrightarrow  - \sqrt {{t_1}}  + \sqrt {{t_2}}  = 2\sqrt {{t_1}} \\ \Leftrightarrow \sqrt {{t_2}}  = 3\sqrt {{t_1}}  \Leftrightarrow {t_2} = 9{t_1}\left( 3 \right)\end{array}\]

Theo định lý Viet ta có \[\left\{ {\begin{array}{*{20}{c}}{{t_1} + {t_2} = 3m + 4(4)}\\{{t_1}{t_2} = {m^2}(5)}\end{array}} \right.\]