Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu Tóm tắt lý thuyết và bài tập trắc nghiệm về tiếp tuyến của đồ thị hàm số, tài liệu bao gồm 25 trang. Tài liệu được tổng hợp từ các tài liệu ôn thi hay nhất  giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kỳ thi sắp hới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây

Tóm tắt lý thuyết và bài tập trắc nghiệm về tiếp tuyến của đồ thị hàm số

CHỦ ĐỀ 7. TIẾP TUYẾN CỦA ĐỒ THỊ HÀM SỐ

A. Kỹ năng cơ bản

Bài toán 1: Các dạng phương trình tiếp tuyến thường gặp.

Cho hàm số \[y = f(x)\], gọi đồ thị của hàm số là (C).

Dạng 1. Viết phương trình tiếp tuyến của đồ thị hàm số (C) : \[y = f(x)\] tại \[M({x_0};{y_0})\]

Phương pháp

Bước 1. Tính \[y = f'(x)\] suy ra hệ số góc của phương trình tiếp tuyến là \[k = y'({x_0})\]

Bước 2. Phương trình tiếp tuyến của đồ thị (C) tại điểm\[M({x_0};{y_0})\] có dạng

\[y - {y_0} = f'({x_0})(x - {x_0})\]

Chú ý:

Nếu đề bài yêu cầu viết phương trình tiếp tuyến tại điểm có hoành độ x₀ thì khi đó ta tìm y₀ bằng cách thế vào hàm số ban đầu, tức \[{y_0} = f({x_0})\]. Nếu đề cho y₀ ta thay vào hàm số để giải ra x_0.

Nếu đề bài yêu cầu viết phương trình tiếp tuyến tại các giao điểm của đồ thị (C): \[y = f(x)\]và đường thẳng \[d:y = ax + b\]. Khi đó các hoành độ tiếp điểm là nghiệm của phương trình hoành độ giao điểm giữa d và (C).

Sử dụng máy tính:

Phương trình tiếp tuyến cần tìm có dạng \[d:y = ax + b\]

Bước 1: Tìm hệ số góc tiếp tuyến \[k = y'({x_0})\]. Nhập  bằng cách nhấn  sau đó nhấn = ta được a.

Bước 2: Sau đó nhân với −X tiếp tục nhấn phím \[ + f(x)CALC\]\[X = {x_0}\] nhấn phím = ta được b.

Ví dụ minh họa

Ví dụ 1. Cho hàm số \[(C):y = {x^3} + 3{x^2}\]. Phương trình tiếp tuyến của đồ thị (C) tại điểm M (1;4) là

A. \[y =  - 9x + 5\].

B. \[y = 9x + 5\].

C. \[y =  - 9x - 5\].

D. \[y = 9x - 5\].

Hướng dẫn giải

Ta có \[y' = 3{x^2} + 6x \Rightarrow k = y'(1) = 9\]. Phương trình tiếp tuyến tại M (1;4) là

\[d:y = y'({x_0})(x - {x_0}) + {y_0} = 9(x - 1) + 4 = 9x - 5\]. Chọn đáp án D.

Sử dụng máy tính:

Nhập 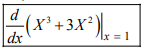 nhấn dấu = ta được 9.

Sau đó nhân với ( −X ) nhấn dấu \[ + {X^3} + 3{X^2}\] \[CALC\] \[X = 1\] nhấn phím = ta được −5 .

Vậy phương trình tiếp tuyến tại M là \[y = 9x - 5\].

Ví dụ 2. Cho hàm số \[y =  - 2{x^3} + 6{x^2} - 5\]. Phương trình tiếp tuyến của (C) tại điểm M thuộc (C) và có hoành độ bằng 3.

A. \[y =  - 18x + 49\].

B. \[y =  - 18x - 49\].

C. \[y = 18x + 49\].

D. \[y = 18x - 49\].

Hướng dẫn giải

Ta có \[y' =  - 6{x^2} + 12x\]. Với x₀ = 3 ⇒ y₀ = − 5 ⇒  M (3;−5) và hệ số góc \[k = y'(3) =  - 18\]

Vậy phương trình tiếp tuyến tại M là \[y =  - 18(x - 3) - 5 =  - 18x + 49\]. Chọn đáp án A.

Sử dụng máy tính:

Nhập nhấn dấu = ta được −18 .

Sau đó nhân với ( −X ) nhấn dấu + \[ - 2{X^3} + 6{X^2} - 5\] \[CALC\] \[X = 3\] nhấn dấu = ta được 49 .

Vậy phương trình tiếp tuyến tại M là \[y =  - 18x + 49\].

Ví dụ 3. Cho hàm số (C): \[y = \frac{1}{4}{x^4} - 2{x^2}\]. Phương trình tiếp tuyến của (C) tại điểm M có hoành độ x₀ > 0, biết y′′(x₀) = −1 là

A. .

B. $y=-3x+1$. \[y =  - 3x - 2\]

C. \[y =  - 3x + \frac{5}{4}\]

D. \[y =  - 3x + \frac{1}{4}\]

Hướng dẫn giải

Ta có \[y' = {x^3} - 4x,y'' = 3{x^2} - 4\]. Mà

y′′(x₀) = −1 ⇒ \[3x_0^2 - 4 =  - 1 \Leftrightarrow x_0^2 = 1 \Leftrightarrow {x_0} = 1\] (vì x₀ > 0 ).

Vậy \[{y_0} =  - \frac{7}{4}\], suy ra \[k = y'(1) =  - 3\].

Vậy phương trình tiếp tuyến tại M là

\[d:y =  - 3(x - 1) - \frac{7}{4} \Rightarrow y =  - 3x + \frac{5}{4}\] ⋅Chọn đáp án C.

Sử dụng máy tính:

Nhập 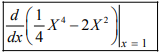 nhấn dấu = ta được −3 .

Sau đó nhân với ( −X ) nhấn dấu + \[\frac{1}{4}{X^4} - 2{X^2}\] \[CALC\] \[X = 1\] ta được \[\frac{5}{4}\].

Vậy phương trình tiếp tuyến là \[y =  - 3x + \frac{5}{4}\]⋅

Dạng 2. Viết phương trình tiếp tuyến của đồ thị hàm số (C): \[y = f(x)\] có hệ số góc k cho trước.

Phương pháp

Bước 1. Gọi \[M({x_0};{y_0})\]là tiếp điểm và tính \[y' = f'(x)\]

Bước 2. Hệ số góc tiếp tuyến là \[k = f'({x_0})\]. Giải phương trình này tìm được x₀, thay vào hàm số được y₀

Bước 3. Với mỗi tiếp điểm ta tìm được các tiếp tuyến tương ứng

d: \[y - {y_0} = f'({x_0})(x - {x_0})\]

Chú ý: Đề bài thường cho hệ số góc tiếp tuyến dưới các dạng sau:

Tiếp tuyến d // ∆: \[y = ax + b\] ⇒ hệ số góc của tiếp tuyến là k = a.

Tiếp tuyến d ⊥ ∆: \[y = ax + b\] (a ≠ 0) ⇔ hệ số góc của tiếp tuyến là k = −\[\frac{1}{a}\] ⋅

Tiếp tuyến tạo với trục hoành một góc α thì hệ số góc của tiếp tuyến d là k = ± tan α

Sử dụng máy tính:

Nhập \[k( - X) + f(x)\] \[CALC\] \[X = {x_0}\] nhấn dấu = ta được b. Phương trình tiếp tuyến là \[y = kx + b\]

Ví dụ minh họa

Ví dụ 1. Cho hàm số (C): \[y = {x^3} - 3x + 2\]. Phương trình tiếp tuyến của (C) biết hệ số góc của tiếp tuyến đó bằng 9 là:

A. \[\left[ {\begin{array}{*{20}{c}}{y = 9x - 14}\\{y = 9x + 18}\end{array}} \right.\]

B. \[\left[ {\begin{array}{*{20}{c}}{y = 9x + 15}\\{y = 9x - 11}\end{array}} \right.\]

C. \[\left[ {\begin{array}{*{20}{c}}{y = 9x - 1}\\{y = 9x + 4}\end{array}} \right.\]

D. \[\left[ {\begin{array}{*{20}{c}}{y = 9x + 8}\\{y = 9x + 5}\end{array}} \right.\]

Hướng dẫn giải

Ta có \[y' = 3{x^2} - 3\].

Vậy \[k = y'({x_0}) = 9 \Leftrightarrow 3x_0^2 - 3 = 9 \Leftrightarrow x_0^2 = 4\]

\[ \Leftrightarrow {x_0} = 2 \vee {x_0} =  - 2.\]

Với x₀ = 2 ⇒ y₀ = 4 ta có tiếp điểm M (2;4) .

Phương trình tiếp tuyến tại M là

\[y = 9(x - 2) + 4 \Rightarrow y = 9x - 14.\]

Với x₀ = − 2 ⇒ y₀ = 0 ta có tiếp điểm N (−2;0).

Phương trình tiếp tuyến tại N là \[y = 9(x + 2) + 0 \Rightarrow y = 9x + 18.\]

Vậy có hai tiếp tuyến cần tìm là \[y = 9x - 14\]và \[y = 9x + 18.\]

Chọn đáp án A.

Sử dụng máy tính:

Với x₀ = 2 ta nhập \[9( - X) + {X^3} - 3{X^2} + 2\] \[CALC\] \[X = 2\] nhấn dấu = ta được −14

⇒ \[y = 9x - 14\].

Với x₀ = −2 ta nhập \[9( - X) + {X^3} - 3{X^2} + 2\] \[CALC\] \[X =  - 2\] nhấn dấu = ta được 18 ⇒\[y = 9x + 18.\]

Ví dụ 2. Cho hàm số (C) : \[y = \frac{{2x + 1}}{{x + 2}}\]. Viết phương trình tiếp tuyến của (C) biết tiếp tuyến song song với đường thẳng có phương trình ∆ : \[3x - y + 2 = 0\].

A. \[y = 3x - 2\].

B. \[y = 3x + 14.\]

C. \[y = 3x + 5.\]

D. \[y = 3x - 8.\]

Hướng dẫn giải

Ta có \[y' = \frac{3}{{{{\left( {x + 2} \right)}^2}}},\Delta :3x - y + 2 = 0 \Rightarrow y = 3x + 2\].

Do tiếp tuyến song song với đường thẳng ∆ nên

\[\begin{array}{l}k = \frac{3}{{{{\left( {{x_0} + 2} \right)}^2}}} = 3 \Leftrightarrow {\left( {{x_0} + 2} \right)^2} = 1\\ \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{{x_0} + 2 = 1}\\{{x_0} + 2 =  - 1}\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{{x_0} =  - 1}\\{{x_0} =  - 3}\end{array}} \right.\end{array}\]

Với x₀ = −1 nhập \[3( - X) + \frac{{2X + 1}}{{X + 2}}\] \[CALC\] \[X =  - 1\] nhấn dấu = ta được 2, suy ra \[d:y = 3x + 2\] (loại do trùng với ∆ ).

Với x₀ = −3 \[CALC\] \[X =  - 3\] nhấn dấu = ta được 14 ⇒ \[d:y = 3x + 14\].

Vậy phương trình tiếp tuyến là \[d:y = 3x + 14\]. Chọn đáp án B.

Dạng 3. Viết phương trình tiếp tuyến của đồ thị hàm số (C) :\[y = f(x)\] biết tiếp tuyến đi qua điểm \[A({x_A};{y_A})\]

Phương pháp

Cách 1.

Bước 1: Phương trình tiếp tuyến đi qua \[A({x_A};{y_A})\] hệ số góc k có dạng

\[d:y = k(x - {x_A}) + {y_A}\] (∗)

Bước 2: d là tiếp tuyến của (C) khi và chỉ khi hệ sau có nghiệm:

\[\left\{ {\begin{array}{*{20}{c}}{f(x) = k(x - {x_A}) + {y_A}}\\{f'(x) = k}\end{array}} \right.\]

Bước 3: Giải hệ này tìm được x suy ra k và thế vào phương trình (∗), ta được tiếp tuyến cần tìm.

Cách 2.

Bước 1. Gọi \[M\left( {{x_0};f({x_0})} \right)\] là tiếp điểm và tính hệ số góc tiếp tuyến \[k = y'({x_0}) = f'({x_0})\]

Bước 2. Phương trình tiếp tuyến có dạng: \[d:y = y'({x_0})(x - {x_0}) + {y_0}\] (∗∗).

Do điểm \[A({x_A};{y_A}) \in d\] nên \[{y_A} = y'({x_0})({x_A} - {x_0}) + {y_0}\] giải phương trình này ta tìm được x₀.

Bước 3. Thế x₀ vào (∗∗) ta được tiếp tuyến cần tìm.

Chú ý: Đối với dạng viết phương trình tiếp tuyến đi qua điểm việc tính toán tương đối mất thời gian. Ta có thể sử dụng máy tính thay các đáp án: Cho \[f(x)\] bằng kết quả các đáp án. Vào MODE → 5 → 4 nhập hệ số phương trình. Thông thường máy tính cho số nghiệm thực nhỏ hơn số bậc của phương trình là 1 thì ta chọn đáp án đó.

Ví dụ minh họa

Ví dụ. Cho hàm số (C) : \[y =  - 4{x^3} + 3x + 1\]. Viết phương trình tiếp tuyến của (C) biết tiếp tuyến đi qua điểm A(−1;2).

A. \[\left[ {\begin{array}{*{20}{c}}{y =  - 9x - 7}\\{y = 2}\end{array}} \right.\]

B. \[\left[ {\begin{array}{*{20}{c}}{y = 4x + 2}\\{y = x + 1}\end{array}} \right.\]

C. \[\left[ {\begin{array}{*{20}{c}}{y = x - 7}\\{y = 3x - 5}\end{array}} \right.\]

D. \[\left[ {\begin{array}{*{20}{c}}{y =  - x - 5}\\{y = 2x - 2}\end{array}} \right.\]

Hướng dẫn giải

Ta có \[y' =  - 12{x^2} + 3\]

Tiếp tuyến của (C) đi qua A(−1;2) với hệ số góc k có phương trình là \[d:y = k(x + 1) + 2\]

d là tiếp tuyến của (C) khi và chỉ khi hệ sau có nghiệm:

\[\left\{ {\begin{array}{*{20}{c}}{ - 4{x^3} + 3x + 1 = k(x + 1) + 2(1)}\\{ - 12{x^2} + 3 = k(2)}\end{array}} \right.\]

Thay k từ (2) vào (1) ta được

\[ - 4{x^3} + 3x + 1 = ( - 12{x^2} + 3)(x + 1) + 2\]

\[\begin{array}{l} \Leftrightarrow 8{x^3} + 12{x^2} - 4 = 0\\ \Leftrightarrow \left( {x - \frac{1}{2}} \right){(x + 1)^2} = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x =  - 1}\\{x = \frac{1}{2}}\end{array}} \right.\end{array}\]

Với x = −1 ⇒ k = − 9. Phương trình tiếp tuyến là \[y =  - 9x - 7.\]

Với \[x = \frac{1}{2}\]⇒ k = 0. Phương trình tiếp tuyến là y = 2. Chọn đáp án A.

Dạng 4. Viết phương trình tiếp tuyến chung của hai đồ thị hàm số (C₁): \[y = f(x)\] và (C₂) : \[y = g(x)\]

Phương pháp

Bước 1. Gọi d tiếp tuyến chung của (C₁), (C₂) và x₀ là hoành độ tiếp điểm của d và (C₁) thì phương trình d có dạng \[y = y'({x_0})(x - {x_0}) + {y_0}\] (***)

Bước 2. Dùng điều kiện tiếp xúc của d và (C₂), tìm được x₀.

Bước 3. Thế x₀ vào (***) ta được tiếp tuyến cần tìm.

Ví dụ minh họa

Ví dụ. Cho hai hàm số:

\[({C_1}):y = f(x) = 2\sqrt x ,(x > 0)\]

và \[({C_2}):y = g(x) = \frac{1}{2}\sqrt {8 - {x^2}} \], \[( - 2\sqrt 2  < x < 2\sqrt 2 )\]

Phương trình tiếp tuyến chung của hai đồ thị hàm số là:

A. \[y = \frac{1}{2}x + 5\]

B. \[y = \frac{1}{2}x - 1\]

C. \[y = \frac{1}{2}x + 2\]

D. \[y = \frac{1}{2}x - 3\]

Hướng dẫn giải

Gọi d là phương trình tiếp tuyến chung của (C₁), (C₂) và x₀ = a ( a > 0 và \[ - 2\sqrt 2  < x < 2\sqrt 2 \]) là hoành độ tiếp điểm của d với (C₁) thì phương trình d là

\[y = y'(x)(x - a) + {y_0} = \frac{1}{{\sqrt a }}(x - a) + 2\sqrt a .\]

d tiếp xúc với (C₂) khi và chỉ khi hệ sau có nghiệm: \[\left\{ {\begin{array}{*{20}{c}}{\frac{1}{2}\sqrt {8 - {x^2}}  = \frac{x}{{\sqrt a }} + \sqrt a (1)}\\{\frac{{ - x}}{{2\sqrt {8 - {x^2}} }} = \frac{1}{{\sqrt a }}(2)}\end{array}} \right.\]

Thay (2) vào (1) ta được phương trình hoành độ tiếp điểm của d và (C₂).

\[\begin{array}{l}\frac{1}{2}\sqrt {8 - {x^2}}  =  - \frac{{{x^2}}}{{2\sqrt {8 - {x^2}} }} - \frac{{2\sqrt {8 - {x^2}} }}{x}\\ \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{ - 2\sqrt 2  < x < 2\sqrt 2 }\\{x \ne 0}\\{x(8 - {x^2}) =  - {x^3} - 4(8 - {x^2})}\end{array}} \right.\end{array}\]

\[ \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{ - 2\sqrt 2  < x < 2\sqrt 2 }\\{x \ne 0}\\{{x^2} - 2x - 8 = 0}\end{array} \Leftrightarrow x =  - 2} \right.\]

Thay x = −2 vào (2) ta được \[\frac{1}{{\sqrt a }} = \frac{1}{2} \Leftrightarrow a = 4 \Rightarrow {x_0} = 4\]. Vậy phương trình tiếp tuyến chung cần tìm là \[y = \frac{1}{2}x + 2\]. Chọn đáp án C.