Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu Tìm cực trị của hàm số hợp khi biết đồ thị hàm số, tài liệu bao gồm 38 trang. Tài liệu được tổng hợp từ các tài liệu ôn thi hay nhất  giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kỳ thi sắp hới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây

Tìm cực trị của hàm số hợp khi biết đồ thị hàm số

TÌM CỰC TRỊ CỦA HÀM SỐ HỢP \[f\left( {u(x)} \right)\] KHI BIẾT ĐỒ THỊ HÀM SỐ \[f(x)\]

Kiến thức cần nhớ:

Đạo hàm của hàm số hợp:

\[g(x) = f\left[ {u(x)} \right] \Rightarrow g'(x) = u'(x).f'\left[ {u(x)} \right]\]

\[g'(x) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{u'(x) = 0}\\{f'\left[ {u(x)} \right] = 0}\end{array}} \right.\]

Lập bảng biến thiên của hàm số \[y = f(x)\] khi biết đồ thị hàm số \[y = f'(x)\]

B1. Xác định giao điểm của đồ thị hàm số \[y = f'(x)\] với trục hoành

B2: Xét dấu của hàm số \[y = f'(x)\], ta làm như sau

Phần đồ thị của \[y = f'(x)\] nằm bên trên trục hoành trong khoảng (a;b) thì \[f'(x) > 0\], \[x \in (a;b)\]

Phần đồ thị của \[y = f'(x)\] nằm bên dưới trục hoành trong khoảng (a;b) thì \[f'(x) < 0\], \[x \in (a;b)\]

Lập bảng biến thiên của hàm số \[g'(x) = f'(x) + u'(x)\] khi biết đồ thị hàm số \[y = f'(x)\]

B1: Đạo hàm \[g'(x) = f'(x) + u'(x)\]. Cho \[g'(x) = 0 \Leftrightarrow f'(x) =  - u'(x)\]

B2. Xác định giao điểm của đồ thị hàm số\[y = f'(x)\]và đồ thị hàm số \[y =  - u'(x)\]

B3: Xét dấu của hàm số \[y = g'(x)\], ta làm như sau

Phần đồ thị của\[f'(x)\]nằm bên trên đồ thị \[ - u'(x)\] trong khoảng (a;b) thì \[g'(x) > 0\], \[x \in (a;b)\]

Phần đồ thị của\[f'(x)\]nằm bên dưới đồ thị \[ - u'(x)\]trong khoảng (a;b) thì \[g'(x) < 0\], \[x \in (a;b)\]

Bài tập mẫu

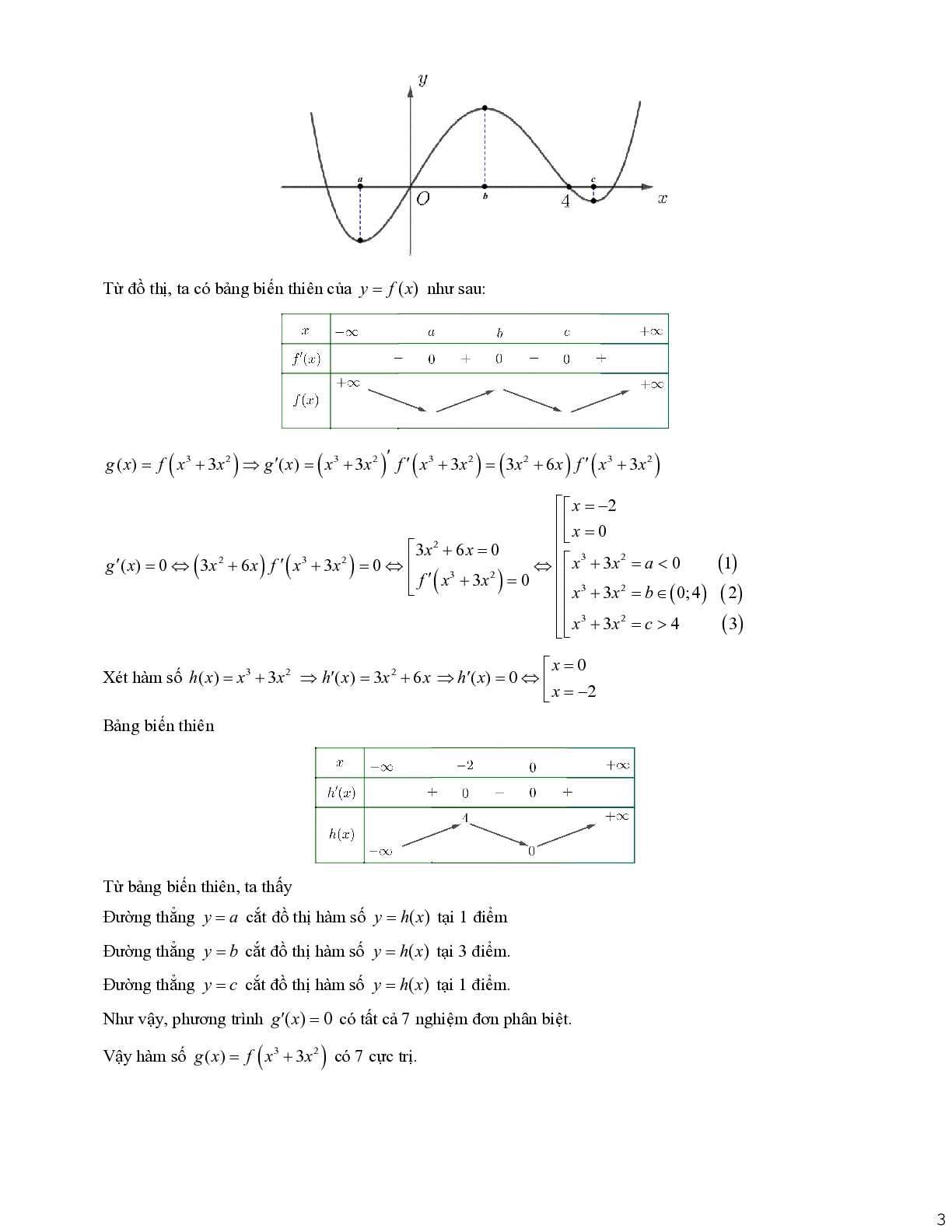
Cho hàm số bậc bốn \[y = f(x)\] có đồ thị như hình bên

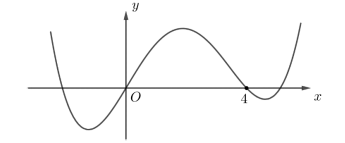
Số điểm cực trị của hàm số \[g(x) = f\left( {{x^3} + 3{x^2}} \right)\]là

A. 5 .

B. 3

C. 7 .

D. 11

Phân tích hướng dẫn giải

1. Dạng toán: Đây là dạng toán tìm số cực trị của hàm hợp \[f\left( {u(x)} \right)\]khi biết đồ thị hàm số\[f(x)\].

2. Kiến thức cần nhớ:

Đạo hàm của hàm hợp: \[\left[ {f\left( {u(x)} \right)} \right]' = u'(x).f'(u)\]

Định lí về cực trị của hàm số:

Cho hàm số \[y = f(x)\] xác định trên D .

Điểm x₀ Î D là điểm cực trị của hàm số\[y = f(x)\] khi \[f'({x_0}) = 0\] hoặc \[f'({x_0})\] không xác định và \[f'(x)\]đổi dấu khi đi qua x₀.

Sự tương giao của hai đồ thị:

Hoành độ giao điểm của hai đồ thị hàm số \[y = f(x)\] và \[y = g(x)\] là nghiệm của phương trình \[f(x) = g(x)\] (1)

Số nghiệm của phương trình (1) bằng số giao điểm của hai cực trị.

Tính chất đổi dấu của biểu thức:

Gọi x = a là một nghiệm của phương trình: \[f(x) = 0\]. Khi đó

Nếu x = a là nghiệm bội bậc chẵn ((x - a)², (x - a)⁴, ...) thì hàm số \[y = f(x)\]không đổi dấu khi đi qua a .

Nếu x = a là nghiệm đơn hoặc nghiệm bội bậc lẻ ((x - a), (x - a)³, ...) thì hàm số \[y = f(x)\] đổi dấu khi đi qua a.

3. Hướng giải:

B1: Tính đạo hàm của hàm số: \[g(x) = f\left( {{x^3} + 3{x^2}} \right)\]

B2: Dựa vào đồ thị của hàm \[f(x)\] ta suy ra số nghiệm của phương trình : \[g'(x) = 0\]

B3: Lập bảng biến thiên của hàm số \[g(x) = f\left( {{x^3} + 3{x^2}} \right)\]và suy ra số cực trị.

Từ đó, ta có thể giải bài toán cụ thể như sau:

Lời giải

Chọn B

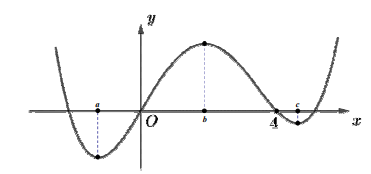
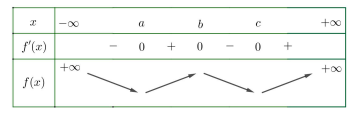
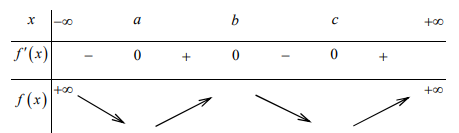
Từ đồ thị, ta có bảng biến thiên của \[y = f(x)\] như sau:

\[\begin{array}{l}g(x) = f\left( {{x^3} + 3{x^2}} \right)\\ \Rightarrow g'(x) = \left( {{x^3} + 3{x^2}} \right)'f'\left( {{x^3} + 3{x^2}} \right)\\ = \left( {3{x^2} + 6x} \right)f'\left( {{x^3} + 3{x^2}} \right)\end{array}\]

\[\begin{array}{l}g'(x) = 0 \Leftrightarrow \left( {{x^3} + 3{x^2}} \right)f'\left( {{x^3} + 3{x^2}} \right)\\ = \left( {3{x^2} + 6x} \right)f'\left( {{x^3} + 3{x^2}} \right) = 0\end{array}\]

\[\begin{array}{l} \Leftrightarrow \left[ \begin{array}{l}3{x^2} + 6x = 0\\f'\left( {{x^3} + 3{x^2}} \right) = 0\end{array} \right.\\ \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{\left[ {\begin{array}{*{20}{c}}{x =  - 2}\\{x = 0}\end{array}} \right.}\\{\begin{array}{*{20}{c}}{{x^3} + 3{x^2} = a < 0(1)}\\{{x^3} + 3{x^2} = b \in (0;4)(2)}\\{{x^3} + 3{x^2} = c > 4(3)}\end{array}}\end{array}} \right.\end{array}\]

Xét hàm số

\[\begin{array}{l}h(x) = {x^3} + 3{x^2} \Rightarrow h'(x) = 3{x^3} + 6x\\ \Rightarrow h'(x) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = 0}\\{x =  - 2}\end{array}} \right.\end{array}\]

Bảng biến thiên

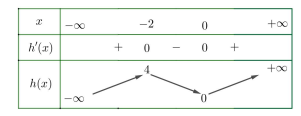
Từ bảng biến thiên, ta thấy

Đường thẳng y = a cắt đồ thị hàm số \[y = h(x)\] tại 1 điểm.

Đường thẳng y = b cắt đồ thị hàm số \[y = h(x)\] tại 3 điểm.

Đường thẳng y = c cắt đồ thị hàm số \[y = h(x)\] tại 1 điểm.

Như vậy, phương trình \[g'(x) = 0\] có tất cả 7 nghiệm đơn phân biệt.

Vậy hàm số \[g(x) = f\left( {{x^3} + 3{x^2}} \right)\] có 7 cực trị.

Cách trình bày khác:

Phân tích hướng dẫn giải

1. Dạng toán: Đây là dạng toán sử dụng đồ thị (hoặc bảng biến thiên) của hàm số \[y = f(x)\](hoặc \[y = f'(x)\]) để tìm cực trị hàm số \[g(x) = f\left[ {u(x)} \right]\].

2. Hướng giải:

B1: Lập bảng biên thiên của hàm số \[y = f(x)\]

Dựa vào đồ thị hàm số\[y = f(x)\] xác định cực trị của hàm số \[y = f(x)\].

Lập bảng biến thiên

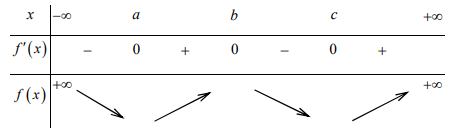
B2: Tìm các điểm tới hạn của hàm số \[g(x) = f\left( {{x^3} + 3{x^2}} \right)\]

Đạo hàm \[g'(x) = \left( {3{x^2} + 6x} \right)f'\left( {{x^3} + 3{x^2}} \right)\]

Cho \[g'(x) = 0\]

\[\begin{array}{l} \Leftrightarrow \left[ \begin{array}{l}3{x^2} + 6x = 0\\f'\left( {{x^3} + 3{x^2}} \right) = 0\end{array} \right.\\ \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{\begin{array}{*{20}{c}}{x = 0}\\{x =  - 2}\end{array}}\\{\begin{array}{*{20}{c}}{{x^3} + 3{x^2} = a;a < 0}\\{{x^3} + 3{x^2} = b;0 < b < 4}\\{{x^3} + 3{x^2} = c;c > 4}\end{array}}\end{array}} \right.\end{array}\]

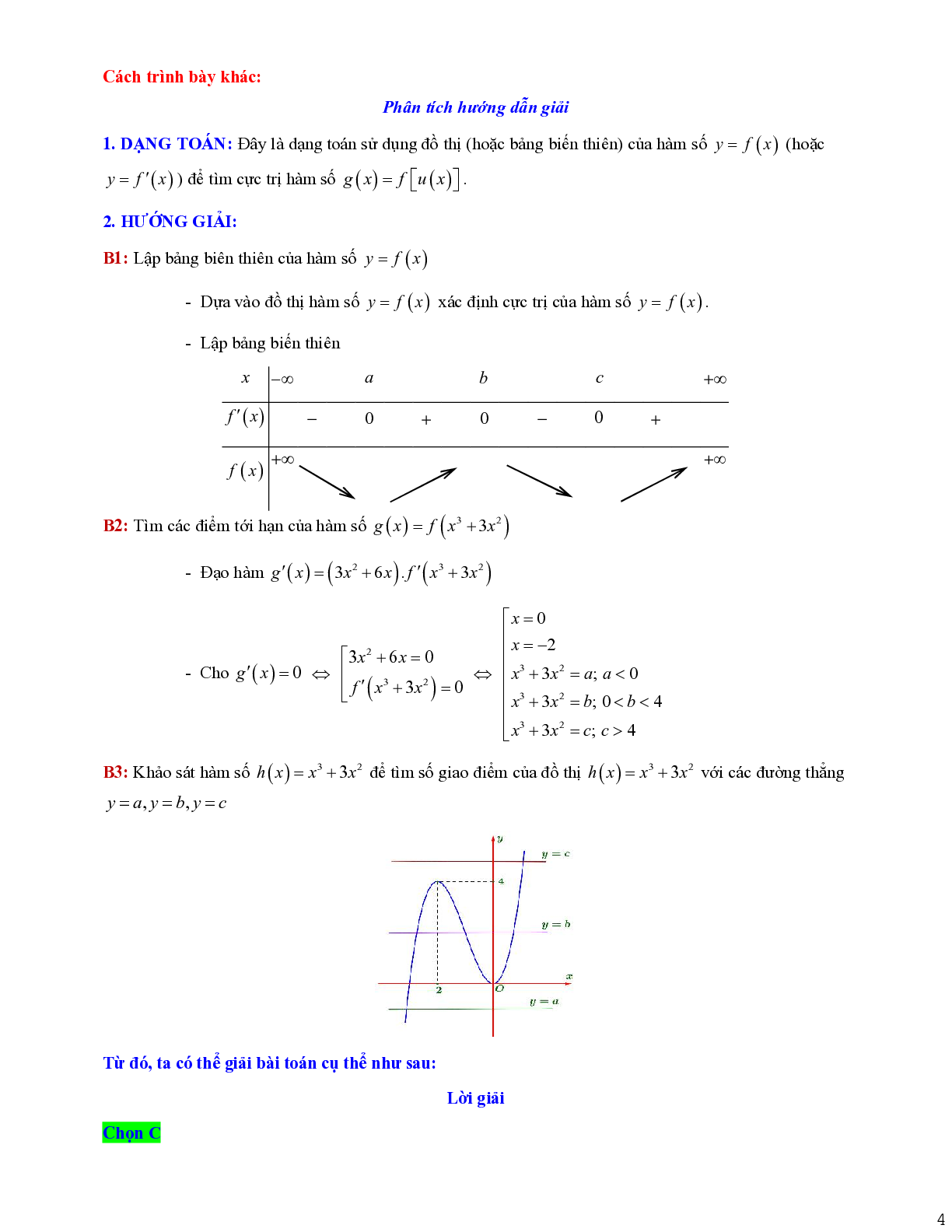
B3: Khảo sát hàm số \[h(x) = {x^3} + 3{x^2}\] để tìm số giao điểm của đồ thị \[h(x) = {x^3} + 3{x^2}\] với các đường thẳng y = a, y = b, y = c

Từ đó, ta có thể giải bài toán cụ thể như sau:

Lời giải

Chọn C

Từ đồ thị ta có bảng biến thiên của hàm số \[y = f(x)\] như sau

Ta có \[g(x) = f\left( {{x^3} + 3{x^2}} \right) \Rightarrow g'(x) = \left( {3{x^2} + 6x} \right)f'\left( {{x^3} + 3{x^2}} \right)\]

Cho \[g'(x) = 0\]

\[\begin{array}{l} \Leftrightarrow \left[ \begin{array}{l}3{x^2} + 6x = 0\\f'\left( {{x^3} + 3{x^2}} \right) = 0\end{array} \right.\\ \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{\begin{array}{*{20}{c}}{x = 0}\\{x =  - 2}\end{array}}\\{\begin{array}{*{20}{c}}{{x^3} + 3{x^2} = a;a < 0}\\{{x^3} + 3{x^2} = b;0 < b < 4}\\{{x^3} + 3{x^2} = c;c > 4}\end{array}}\end{array}} \right.\end{array}\]

Xét hàm số \[h(x) = {x^3} + 3{x^2} \Rightarrow h'(x) = 3{x^3} + 6x\]. Cho \[h'(x) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = 0}\\{x =  - 2}\end{array}} \right.\]

Bảng biến thiên

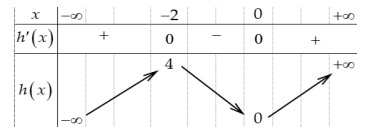
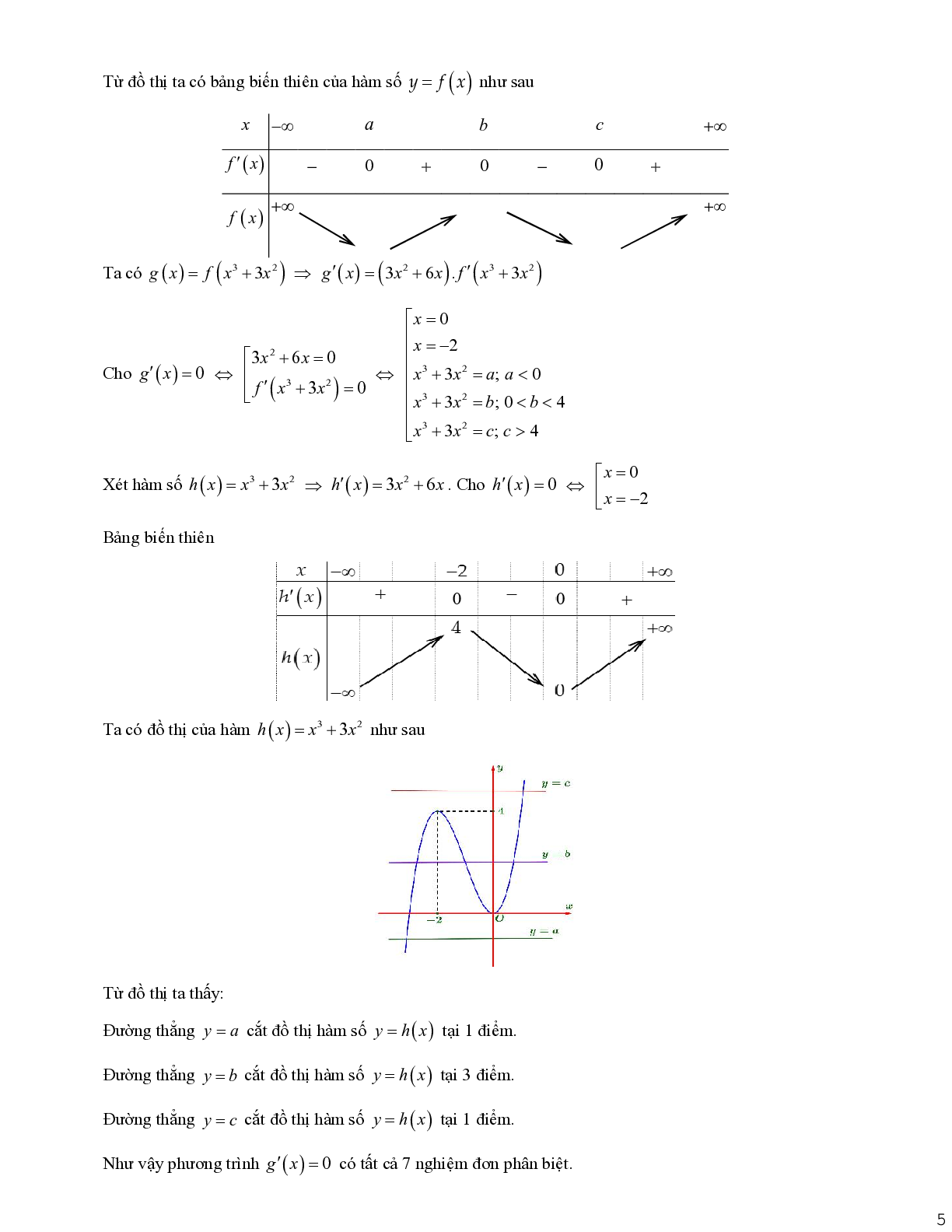
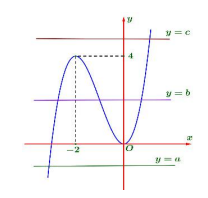
Ta có đồ thị của hàm \[h(x) = {x^3} + 3{x^2}\] như sau

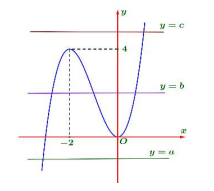
Từ đồ thị ta thấy:

Đường thẳng y = a cắt đồ thị hàm số \[y = h(x)\] tại 1 điểm.

Đường thẳng y = b cắt đồ thị hàm số \[y = h(x)\] tại 3 điểm.

Đường thẳng y = c cắt đồ thị hàm số \[y = h(x)\] tại 1 điểm.

Như vậy, phương trình \[g'(x) = 0\] có tất cả 7 nghiệm đơn phân biệt.

Vậy hàm số \[g(x) = f\left( {{x^3} + 3{x^2}} \right)\] có 7 cực trị.