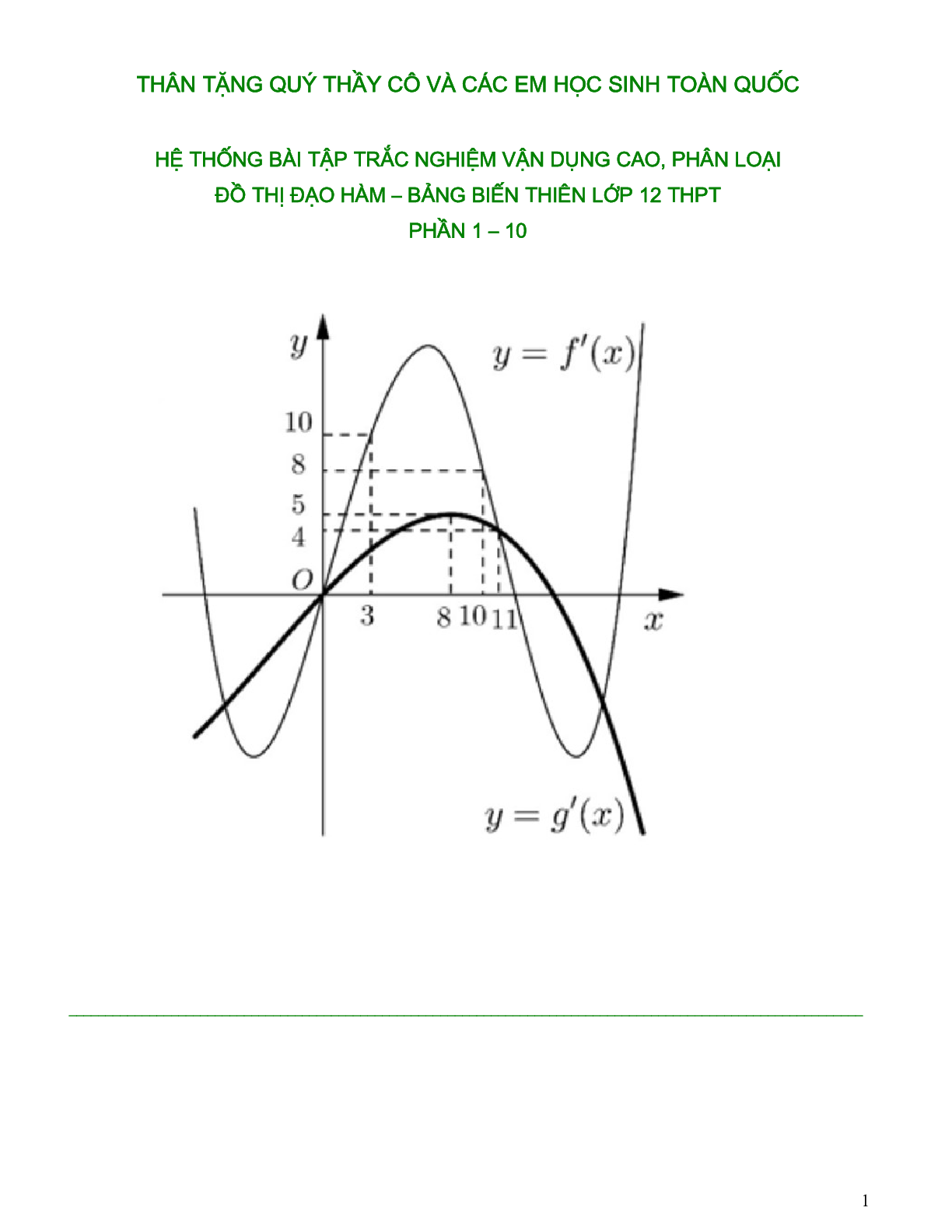
Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu Hệ thống bài tập trắc nghiệm vận dụng cao, phân loại đồ thị đạo hàm - bảng biến thiên phần 1 - 10, tài liệu bao gồm 21 trang. Tài liệu được tổng hợp từ các tài liệu ôn thi hay nhất  giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kỳ thi sắp hới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây

Hệ thống bài tập trắc nghiệm vận dụng cao, phân loại đồ thị đạo hàm - bảng biến thiên phần 1 – 10

Ôn tập đồ thị đạo hàm - bảng biến thiên lớp 12 thpt (lớp bài toán vận dụng cao, phân loại – phần 1)

Câu 1. Cho \[y = f(x)\] có \[f'(x) = {x^3}(x - 5)\]. Hàm số \[g = f({x^2} + 1)\] đồng biến trên khoảng nào ?

A. (0;1)

B. (0;2)

C. (1;6)

D. (6;9)

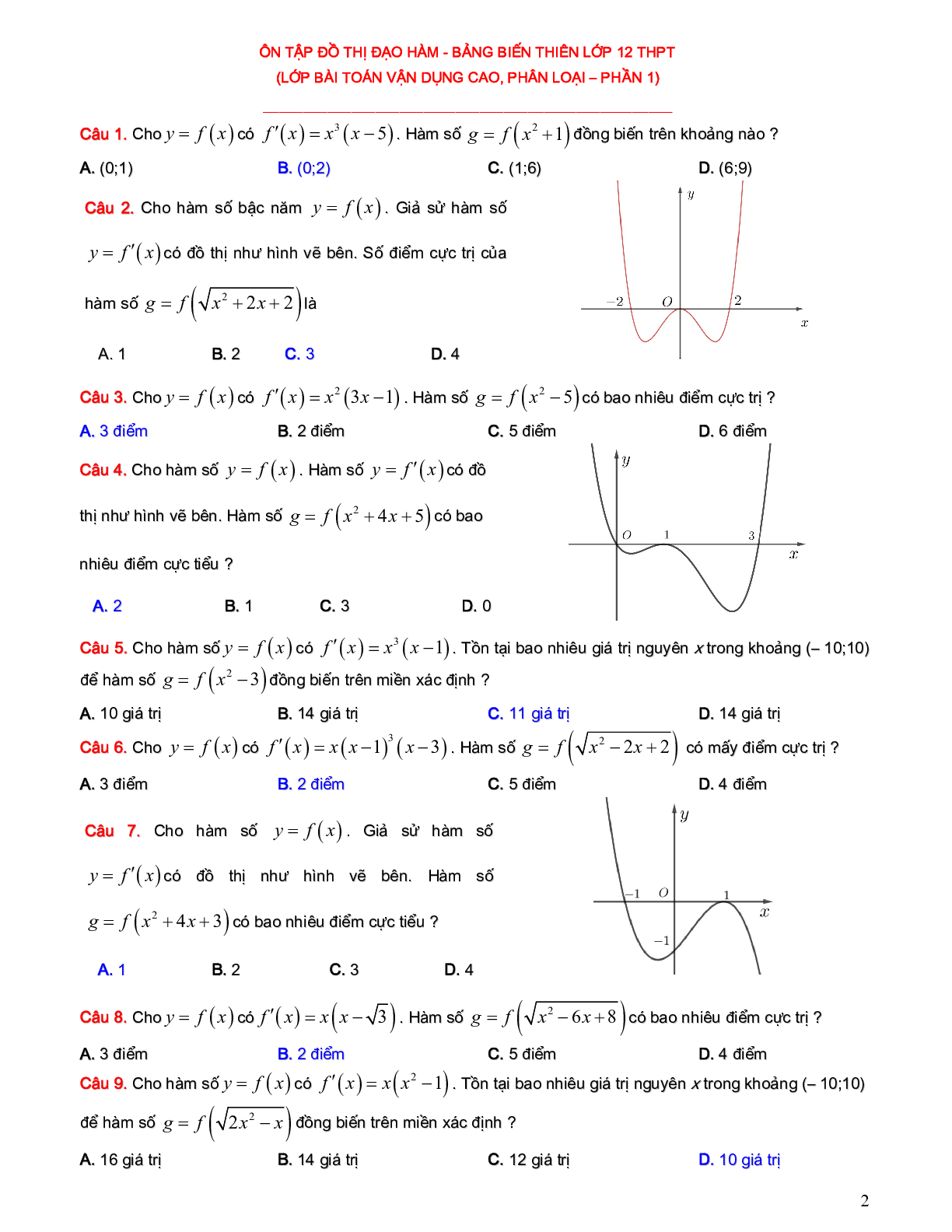
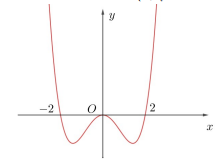
Câu 2. Cho hàm số bậc năm \[y = f(x)\]. Giả sử hàm số \[y = f'(x)\] có đồ thị như hình vẽ bên. Số điểm cực trị của hàm số \[g = f(\sqrt {{x^2} + 2x + 2} )\] là

A. 1

B. 2

C. 3

D. 4

Câu 3. Cho\[y = f(x)\] có \[f'(x) = {x^2}(3x - 1)\]. Hàm số \[g = f({x^2} - 5)\]có bao nhiêu điểm cực trị ?

A. 3 điểm

B. 2 điểm

C. 5 điểm

D. 6 điểm

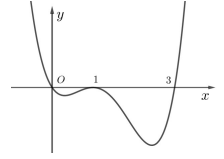
Câu 4. Cho hàm số \[y = f(x)\]. Hàm số \[y = f'(x)\] có đồ thị như hình vẽ bên. Hàm số \[g = f({x^2} + 4x + 5)\]có bao nhiêu điểm cực tiểu ?

A. 2

B. 1

C. 3

D. 0

Câu 5. Cho hàm số \[y = f(x)\] có \[f'(x) = {x^3}(x - 1)\]. Tồn tại bao nhiêu giá trị nguyên x trong khoảng (– 10;10) để hàm số \[g = f({x^2} - 3)\] đồng biến trên miền xác định ?

A. 10 giá trị

B. 14 giá trị

C. 11 giá trị

D. 14 giá trị

Câu 6. Cho\[y = f(x)\] có \[f'(x) = x{(x - 1)^3}(x - 3)\]. Hàm số \[g = f(\sqrt {{x^2} - 2x + 2} )\] có mấy điểm cực trị ?

A. 3 điểm

B. 2 điểm

C. 5 điểm

D. 4 điểm

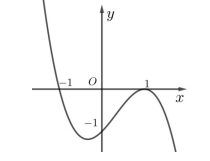
Câu 7. Cho hàm số \[y = f(x)\]. Giả sử hàm số \[y = f'(x)\] có đồ thị như hình vẽ bên. Hàm số \[g = f({x^2} + 4x + 3)\] có bao nhiêu điểm cực tiểu ?

A. 1

B. 2

C. 3

D. 4

Câu 8. Cho\[y = f(x)\] có \[f'(x) = x(x - \sqrt 3 )\]. Hàm số \[g = f(\sqrt {{x^2} - 6x + 8} )\] có bao nhiêu điểm cực trị ?

A. 3 điểm

B. 2 điểm

C. 5 điểm

D. 4 điểm

Câu 9. Cho hàm số\[y = f(x)\] có\[f'(x) = x({x^2} - 1)\]. Tồn tại bao nhiêu giá trị nguyên x trong khoảng (– 10;10) để hàm số \[g = f(\sqrt {2{x^2} - x} )\] đồng biến trên miền xác định ?

A. 16 giá trị

B. 14 giá trị

C. 12 giá trị

D. 10 giá trị

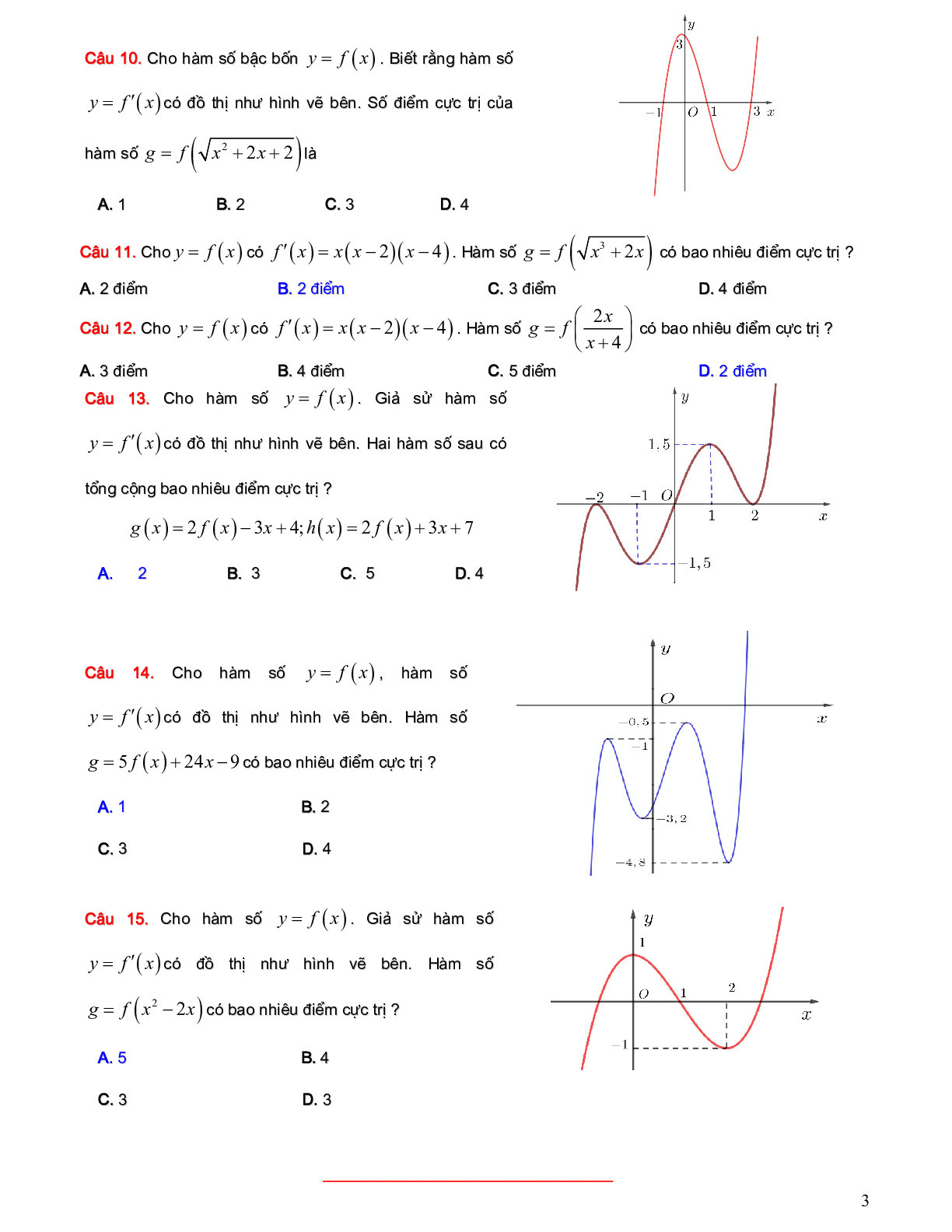
Câu 10. Cho hàm số bậc bốn\[y = f(x)\]. Biết rằng hàm số \[y = f'(x)\] có đồ thị như hình vẽ bên. Số điểm cực trị của hàm số \[g = f(\sqrt {{x^2} + 2x + 2} )\] là

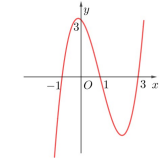
A. 1

B. 2

C. 3

D. 4

Câu 11. Cho \[y = f(x)\] có \[f'(x) = x(x - 2)(x - 4)\]. Hàm số \[g = f(\sqrt {{x^3} + 2x} )\] có bao nhiêu điểm cực trị ?

A. 2 điểm

B. 2 điểm

C. 3 điểm

D. 4 điểm

Câu 12. Cho \[y = f(x)\] có \[f'(x) = x(x - 2)(x - 4)\]. Hàm số \[g = f\left( {\frac{{2x}}{{x + 4}}} \right)\] có bao nhiêu điểm cực trị ?

A. 3 điểm

B. 4 điểm

C. 5 điểm

D. 2 điểm

Câu 13. Cho hàm số \[y = f(x)\]. Giả sử hàm số \[y = f'(x)\] có đồ thị như hình vẽ bên. Hai hàm số sau có tổng cộng bao nhiêu điểm cực trị ?

\[g(x) = 2f(x) - 3x + 4;h(x) = 2f(x) + 3x + 7\]

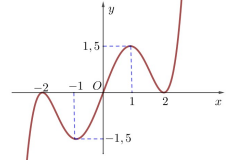
A. 2

B. 3

C. 5

D. 4

Câu 14. Cho hàm số \[y = f(x)\], hàm số \[y = f'(x)\] có đồ thị như hình vẽ bên. Hàm số \[g = 5f(x) + 24x - 9\] có bao nhiêu điểm cực trị ?

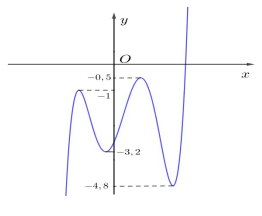
A. 1

B. 2

C. 3

D. 4

Câu 15. Cho hàm số\[y = f(x)\]. Giả sử hàm số \[y = f'(x)\]có đồ thị như hình vẽ bên. Hàm số \[g = f\left( {{x^2} - 2x} \right)\] có bao nhiêu điểm cực trị ?

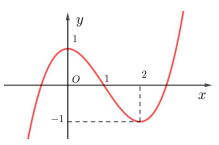
A. 5

B. 4

C. 3

D. 3

Ôn tập đồ thị đạo hàm - bảng biến thiên lớp 12 thpt (lớp bài toán vận dụng cao, phân loại – phần 2)

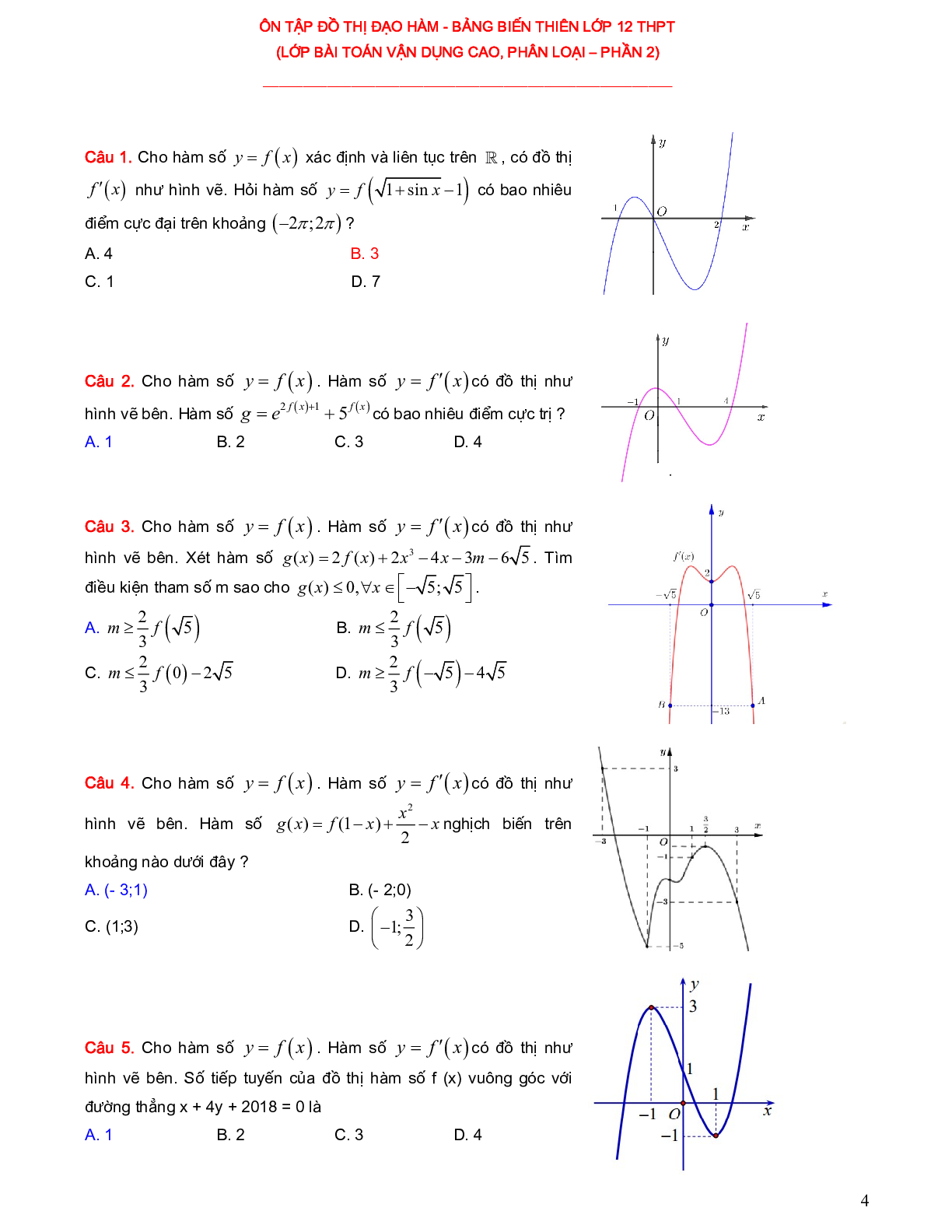
Câu 1. Cho hàm số \[y = f(x)\] xác định và liên tục trên R, có đồ thị \[f'(x)\] như hình vẽ. Hỏi hàm số \[y = f\left( {\sqrt {1 + \sin }  - 1} \right)\]có bao nhiêu điểm cực đại trên khoảng (-2p;2p) ?

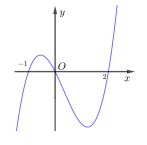
A. 4

B. 3

C. 1

D. 7

Câu 2. Cho hàm số \[y = f(x)\]. Hàm số \[y = f'(x)\] có đồ thị như hình vẽ bên. Hàm số \[g = {e^{2f(x) + 1}} + {5^{f(x)}}\] có bao nhiêu điểm cực trị ?

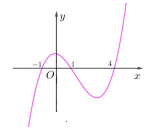
A. 1

B. 2

C. 3

D. 4

Câu 3. Cho hàm số \[y = f(x)\]. Hàm số \[y = f'(x)\] có đồ thị như hình vẽ bên. Xét hàm số \[g(x) = 2f(x) + 2{x^3} - 4x - 3m - 6\sqrt 5 \]. Tìm điều kiện tham số m sao cho \[g(x),\forall x \in \left[ { - \sqrt 5 ;\sqrt 5 } \right]\].

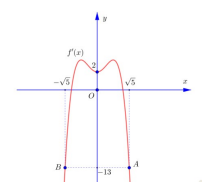
A. \[m \ge \frac{2}{3}f\left( {\sqrt 5 } \right)\]

B. \[m \le \frac{2}{3}f\left( {\sqrt 5 } \right)\]

C. \[m \le \frac{2}{3}f\left( 0 \right) - 2\sqrt 5 \]

D. \[m \ge \frac{2}{3}f\left( { - \sqrt 5 } \right) - 4\sqrt 5 \]

Câu 4. Cho hàm số \[y = f(x)\]. Hàm số \[y = f'(x)\] có đồ thị như hình vẽ bên. Hàm số \[g(x) = f(1 - x) + \frac{{{x^2}}}{2} - x\] nghịch biến trên khoảng nào dưới đây ?

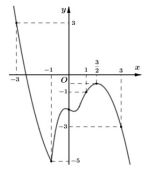
A. (- 3;1)

B. (- 2;0)

C. (1;3)

D. \[\left( { - 1;\frac{3}{2}} \right)\]

Câu 5. Cho hàm số \[y = f(x)\]. Hàm số \[y = f'(x)\] có đồ thị như hình vẽ bên. Số tiếp tuyến của đồ thị hàm số \[f(x)\]vuông góc với đường thẳng x + 4y + 2018 = 0 là

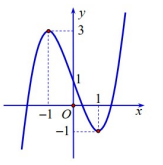
A. 1

B. 2

C. 3

D. 4

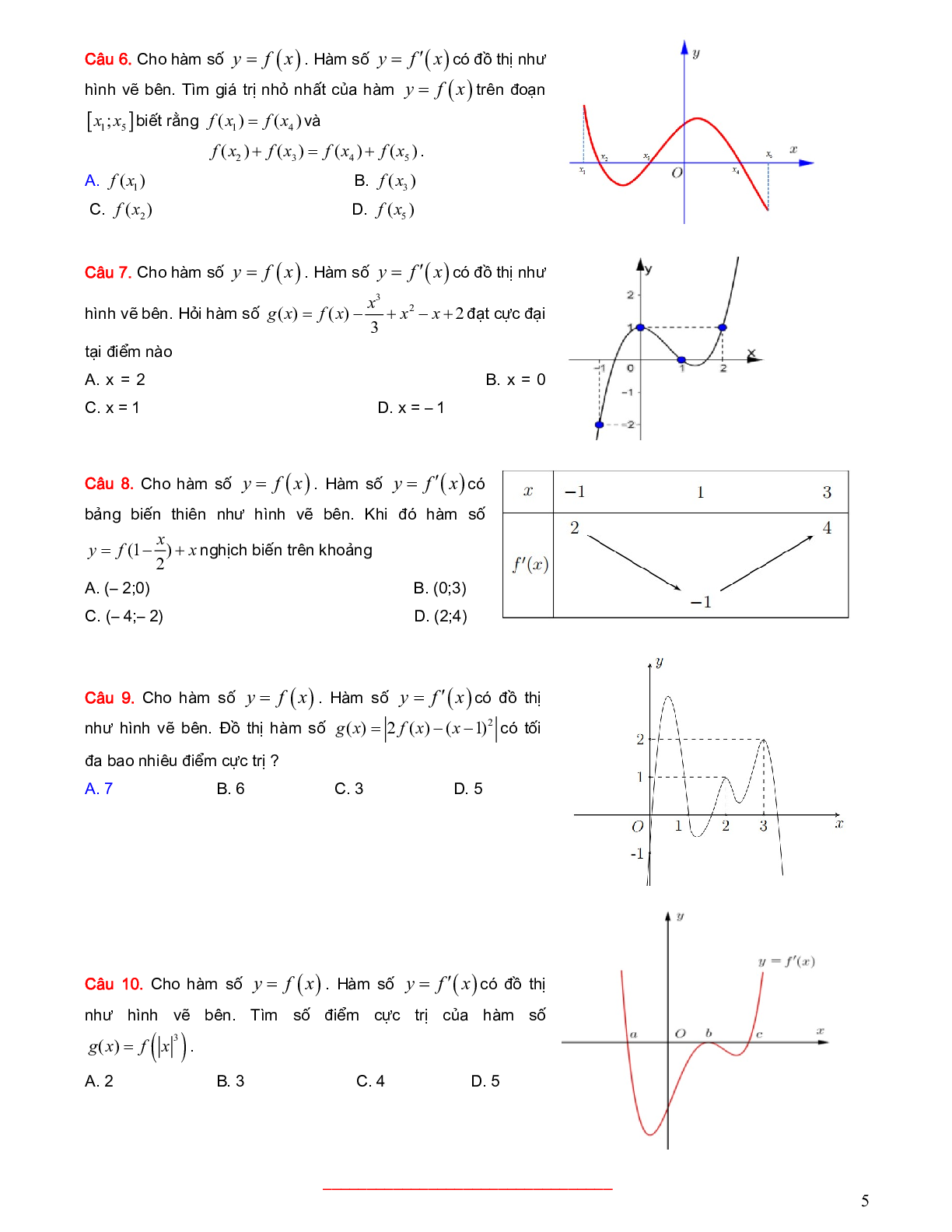
Câu 6. Cho hàm số \[y = f(x)\]. Hàm số \[y = f'(x)\] có đồ thị như hình vẽ bên. Tìm giá trị nhỏ nhất của hàm \[y = f(x)\] trên đoạn \[\left[ {{x_1};{x_5}} \right]\]biết rằng \[f({x_1}) = f({x_4})\] và \[f({x_2}) + f({x_3}) = f({x_4}) + f({x_5})\]

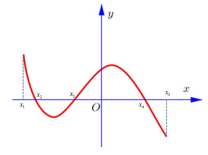
A. \[f({x_1})\]

B. \[f({x_3})\]

C. \[f({x_2})\]

D. \[f({x_5})\]

Câu 7. Cho hàm số \[y = f(x)\]. Hàm số \[y = f'(x)\] có đồ thị như hình vẽ bên. Hỏi hàm số \[g(x) = f(x) - \frac{{{x^3}}}{3} + {x^2} - x + 2\] đạt cực đại tại điểm nào

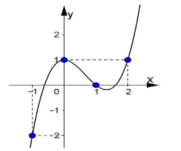
A. x = 2

B. x = 0

C. x = 1

D. x = – 1

Câu 8. Cho hàm số \[y = f(x)\]. Hàm số \[y = f'(x)\] có bảng biến thiên như hình vẽ bên. Khi đó hàm số \[y = f\left( {1 - \frac{x}{2}} \right) + x\]nghịch biến trên khoảng

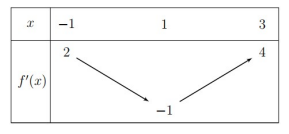
A. (– 2;0)

B. (0;3)

C. (– 4;– 2)

D. (2;4)

Câu 9. Cho hàm số \[y = f(x)\]. Hàm số \[y = f'(x)\] có đồ thị như hình vẽ bên. Đồ thị hàm số \[g(x) = \left| {2f(x) - {{(x - 1)}^2}} \right|\]có tối đa bao nhiêu điểm cực trị ?

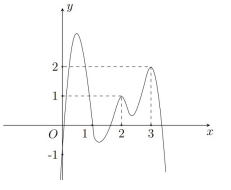
A. 7

B. 6

C. 3

D. 5

Câu 10. Cho hàm số \[y = f(x)\]. Hàm số \[y = f'(x)\] có đồ thị như hình vẽ bên. Tìm số điểm cực trị của hàm số \[g(x) = f\left( {{{\left| x \right|}^3}} \right)\].

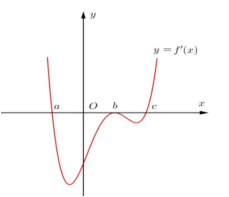
A. 2

B. 3

C. 4

D. 5

Ôn tập đồ thị đạo hàm - bảng biến thiên lớp 12 thpt (lớp bài toán vận dụng cao, phân loại – phần 3)

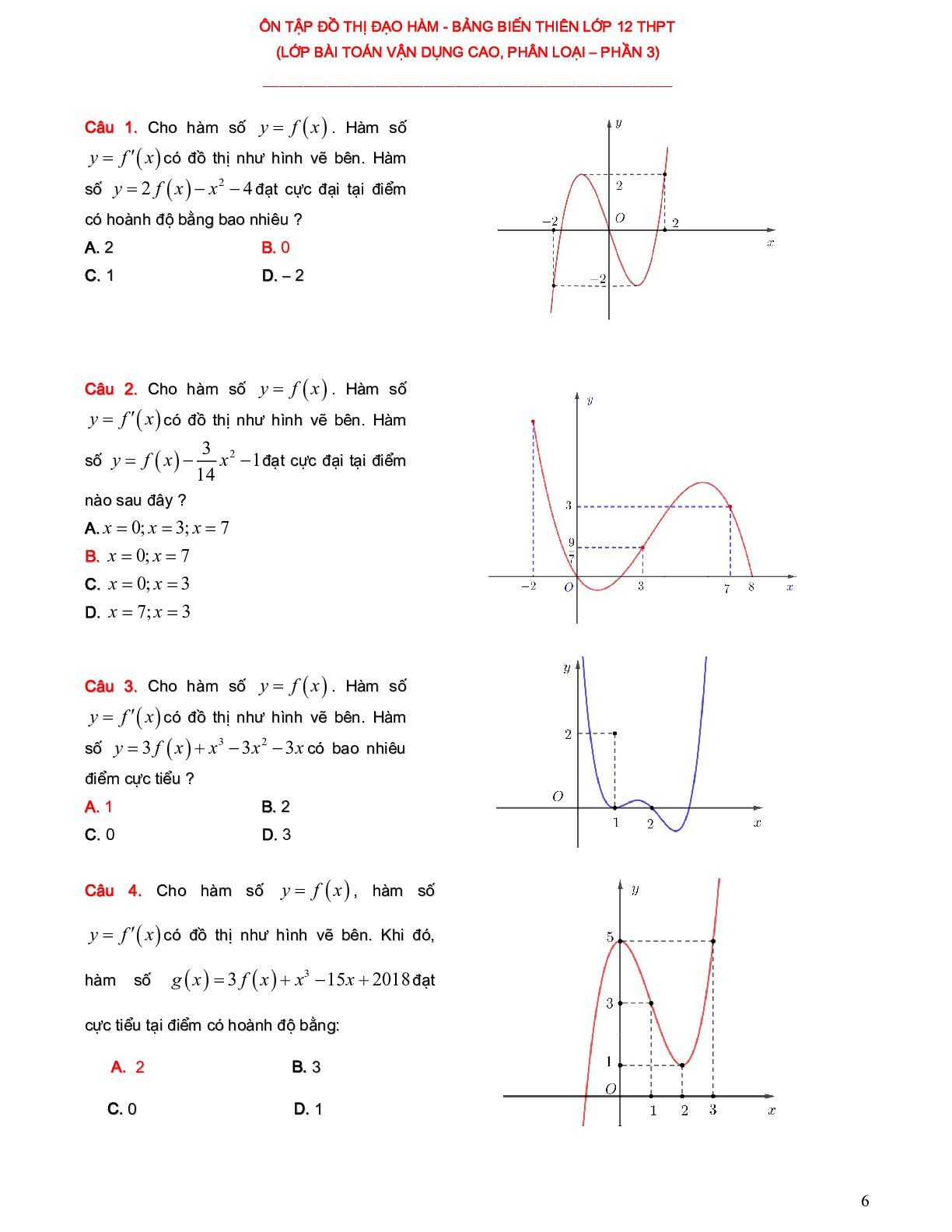
Câu 1. Cho hàm số \[y = f(x)\]. Hàm số \[y = f'(x)\] có đồ thị như hình vẽ bên. Hàm số \[y = 2f\left( x \right) - {x^2} - 4\] đạt cực đại tại điểm có hoành độ bằng bao nhiêu ?

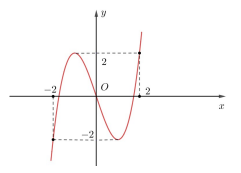
A. 2

B. 0

C. 1

D. – 2

Câu 2. Cho hàm số \[y = f(x)\]. Hàm số \[y = f'(x)\] có đồ thị như hình vẽ bên. Hàm số \[y = f\left( x \right) - \frac{3}{{14}}{x^2} - 1\] đạt cực đại tại điểm nào sau đây ?

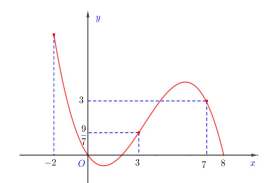
A. x = 0; x = 3; x = 7

B. x = 0; x = 7

C. x = 0; x = 3

D. x = 7; x = 3

Câu 3. Cho hàm số \[y = f(x)\]. Hàm số \[y = f'(x)\] có đồ thị như hình vẽ bên. Hàm số \[y = 3f\left( x \right) + {x^3} - 3{x^2} - 3x\] có bao nhiêu điểm cực tiểu ?

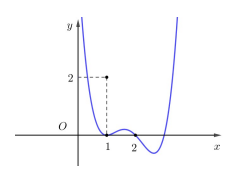
A. 1

B. 2

C. 0

D. 3

Câu 4. Cho hàm số \[y = f(x)\], hàm số \[y = f'(x)\] có đồ thị như hình vẽ bên. Khi đó, hàm số \[g(x) = 3f\left( x \right) + {x^3} - 15x + 2018\] đạt cực tiểu tại điểm có hoành độ bằng:

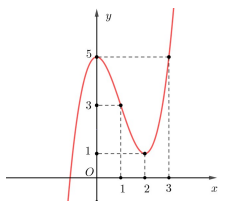
A. 2

B. 3

C. 0

D. 1