Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu Chuyên đề phương pháp tọa độ trong mặt phẳng - Nguyễn Bá Hoàng, tài liệu bao gồm 39 trang. Tài liệu được tổng hợp từ các tài liệu ôn thi hay nhất  giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kỳ thi sắp hới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây

Chuyên đề phương pháp tọa độ trong mặt phẳng - Nguyễn Bá Hoàng

Phương pháp tọa độ trong mặt phẳng

Bài 1. Viết phương trình đường thẳng

I. Nội dung kiến thức.

1. Một số kiến thức về vectơ và toạ độ:

Giá của một vecto là đường thẳng đi qua điểm đầu và điểm cuối của vectơ đó.

Cho hai điểm A, B thì \[\overrightarrow {AB}  = ({x_B} - {x_A};{y_B} - {y_A})\],

\[AB = \left| {\overrightarrow {AB} } \right| = \sqrt {{{({x_B} - {x_A})}^2} + {{({y_B} - {y_A})}^2}} \].

Nếu M là trung điểm của đoạn thẳng AB thì \[{x_M} = \frac{{{x_A} + {x_B}}}{2};{y_M} = \frac{{{y_A} + {y_B}}}{2}\].

Nếu G là trọng tâm của tam giác ABC thì \[{x_G} = 3;{y_M} = \frac{{{y_A} + {y_B} + {y_C}}}{3}\].

\[\overrightarrow u .\overrightarrow v  = \left| {\overrightarrow u } \right|.\left| {\overrightarrow v } \right|.\cos \left( {\overrightarrow u ,\overrightarrow v } \right)\], nếu \[\overrightarrow u  \bot \overrightarrow v \]thì \[\overrightarrow u .\overrightarrow v  = 0;{0^0} < (\overrightarrow u .\overrightarrow v ) < {180^0}\].

2. Vectơ chỉ phương của đường thẳng:

Vectơ \[\overrightarrow u \]được gọi là vectơ chỉ phương của đường thẳng d nếu nó có giá song song hoặc trùng với đường thẳng d.

3. Vectơ pháp tuyến của đường thẳng:

Vectơ \[\overrightarrow n \]được gọi là vectơ pháp tuyến của đường thẳng d nếu nó có giá vuông góc với đường thẳng d.

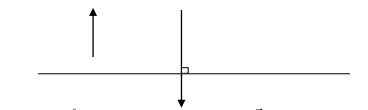
4. Phương trình tham số của đường thẳng:

Đường thẳng d có vectơ chỉ phương \[\overrightarrow u  = (a;b)\] và đi qua điểm M (x₀;y₀) thì có phương trình tham số là: \[\left\{ {\begin{array}{*{20}{c}}{x = {x_0} + at}\\{y = {y_0} + bt}\end{array}} \right.\]0 ở đây t chính là tham số.

5. Phương trình chính tắc của đoạn thẳng: Đường thẳng d có vectơ chỉ phương \[\overrightarrow u  = (a;b)\] và đi qua điểm M (x₀;y₀) thì có phương trình tham số là: \[\frac{{x - {x_0}}}{a} = \frac{{y - {y_0}}}{b}\], chú ý rằng phương trình chính tắc của đoạn thẳng chỉ được viết khi ab ¹ 0.

6. Phương trình tổng quát của đường thẳng:

Đường thẳng d có vectơ pháp tuyến \[\overrightarrow n  = (a;b)\] và đi qua điểm M (x₀;y₀) thì có phương trình tổng quát là: \[a(x - {x_0}) + b(y - {y_0}) = 0\].

Cho đường thẳng \[a:ax + by + c = 0\].

Nếu đường thẳng d' song song với đường thẳng d thì phương trình đường thẳng d ' có dạng \[ax + by + c' = 0\].

Nếu đường thẳng d'' vuông góc với đường thẳng d thì phương trình đường thẳng d '' có dạng \[bx - ay + c'' = 0\].

7. Phương trình đường thẳng theo đoạn chắn:

Đường thẳng d đi qua hai điểm A (a;0), B (0;b) với ab ¹ 0 có phương trình là: \[\frac{x}{a} + \frac{y}{b} - 1 = 0\]

8. Phương trình đường thẳng theo hệ số góc:

Đường thẳng d có hệ số góc k và đi qua điểm M (x₀;y₀) thì có phương trình theo hệ số góc là: \[y = k(x - {x_0}) + {y_0}\], chú ý rằng những đường thẳng song song với trục tung không viết được phương trình theo hệ số góc.

Góc giữa đường thẳng d và trục Ox: Đường thẳng d cắt trục Ox tại M, Mt là tia nằm phía trên trục Ox thì xMt = a là góc giữa đường thẳng d và trục Ox và ta cần lưu ý rằng tan a = k.

Đường thẳng d nếu có hệ số góc là k thì nó có vectơ chỉ phương là \[\overrightarrow u  = (1;k)\]và vectơ pháp tuyến là \[\overrightarrow v  = (k; - 1)\].

Cho đường thẳng d có hệ số góc là k và đường thẳng d ' có hệ số góc là k ' nếu:

\[d \bot d'\] thì \[k.k' =  - 1\].

\[d//d'\] thì \[k = k'\].

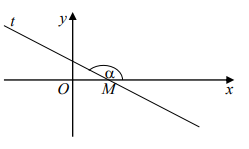
9. Lưu ý: Khi đề bài yêu cầu viết phương trình đường thẳng mà không nói gì ta viết phương trình tổng quát.

10. Vị trí tương đối của hai đường thẳng:

Cho hai đường thẳng : \[\left\{ {\begin{array}{*{20}{c}}{d:ax + by + c = 0}\\{d':a'x + b'y + c' = 0}\end{array}} \right.\]

Để xét vị trí tương đối của d và d ' ta xét số nghiệm của hệ phương trình sau: \[\left\{ {\begin{array}{*{20}{c}}{ax + by + c = 0}\\{a'x + b'y + c' = 0}\end{array}} \right.\]  (I)

Hệ (I) có một nghiệm thì d và d ' cắt nhau.

Hệ (I) vô nghiệm thì d và d ' song song với nhau.

Hệ (I) có vô số nghiệm thì d và d ' trùng nhau.

Nếu a'b'c' ¹ 0 thì:

d và d ' cắt nhau khi và chỉ khi \[\frac{a}{{a'}} \ne \frac{b}{{b'}}\]

d và d ' song song với nhau khi và chỉ khi \[\frac{a}{{a'}} = \frac{b}{{b'}} \ne \frac{c}{{c'}}\]

d và d ' trùng nhau khi và chỉ khi \[\frac{a}{{a'}} = \frac{b}{{b'}} = \frac{c}{{c'}}\]

II. Ví dụ minh hoạ.

Ví dụ 1. Cho hai điểm M(-1;2), N(2;3).

a. Tìm vecto chỉ phương và vecto pháp tuyến của đường thẳng MN;

b. Viết phương trình chính tắc, tham số của đường thẳng MN.

Lời giải

a. Ta có vecto \[\overrightarrow {MN} \] chính là vectơ chỉ phương của đường thẳng MN nên :

\[\overrightarrow {{u_{MN}}}  = (2 - ( - 1);3 - 2) \Leftrightarrow \overrightarrow {{u_{MN}}}  = (3;1)\]

Vectơ pháp tuyến của đường thẳng MN ta lấy được ngay là \[\overrightarrow {{n_{MN}}}  = ( - 1;3)\]

b. Do đường thẳng MN đi qua M(-1;2) và có vectơ chỉ phương \[\overrightarrow {{u_{MN}}}  = (3;1)\] nên ta có : Phương trình tham số của đường thẳng MN là :

\[\left\{ {\begin{array}{*{20}{c}}{x = 3 + ( - 1)t}\\{y = 1 + 2t}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x = 3 - t}\\{y = 1 + 2t}\end{array}} \right.} \right.\]

Phương trình chính tắc của đường thẳng MN là :

 \[\frac{{x - ( - 1)}}{3} = \frac{{y - 2}}{1} \Leftrightarrow \frac{{x + 1}}{3} = \frac{{y - 2}}{1}\]

Ví dụ 2. Cho đường thẳng D có phương trình tham số: \[\left\{ {\begin{array}{*{20}{c}}{x = 1 + 2t}\\{y =  - 3 - t}\end{array}} \right.\]

a. Viết phương trình tổng quát của D;

b. Viết phương trình chính tắc của đường thẳng d đi qua điểm M(2;3) và song song với D;

c. Viết phương trình tổng quát của đường thẳng l đi qua điểm N(4;2) và vuông góc với D.

Lời giải

a. Đường thẳng D có vectơ chỉ phương là \[\overrightarrow u  = (2; - 1)\] nên có vectơ pháp tuyến là \[\overrightarrow n  = (1;2)\]

Chọn tham số t = 0 ta có ngay điểm A(1;-3) nằm trên D.

Phương trình tổng quát của đường thẳng D là :

\[1.(x - 1) + 2.\left[ {y - ( - 3)} \right] = 0 \Leftrightarrow x + 2y - 5 = 0\]

b. Do đường thẳng d song song với D nên đường thẳng d có vectơ chỉ phương là \[\overrightarrow {{u_d}}  = (2; - 1)\]

Phương trình chính tắc của đường thẳng d là : \[\frac{{x - 2}}{2} = \frac{{y - 3}}{{ - 1}}\]

c. Đường thẳng l vuông góc với D nên có vectơ pháp tuyến là \[\overrightarrow {{n_l}}  = (2; - 1)\]

Phương trình tổng quát của đường thẳng l là :

\[2.(x - 4) - 1.(y - 2) = 0 \Leftrightarrow 2x - y - 6 = 0\]

Ví dụ 3. Cho tam giác ABC với A(-1;2), B(2;3), C(4;6).

a. Viết phương trình đường trung tuyến của tam giác kẻ từ B;

b. Tìm toạ độ trực tâm của tam giác ABC.

Lời giải

a. Gọi D là trung điểm của AC, ta có toạ độ của điểm D là : \[D = \left( {\frac{3}{2};4} \right)\]

Ta có \[\overrightarrow {BD}  = \left( {\frac{3}{2} - 2;4 - 3} \right) = \left( {\frac{{ - 1}}{2};1} \right)\] nên vectơ pháp tuyến của đường thẳng BD là: \[\overrightarrow {{n_{BD}}}  = (2;1)\] 

Phương trình đường thẳng BD là : \[2(x - 2) + 1(y - 3) = 0 \Leftrightarrow 2x + y - 7 = 0\]

b. Gọi H là trực tâm của tam giác ABC.

Ta có \[\overrightarrow {BC}  = (2;3)\]là vectơ pháp tuyến của đường thẳng AH nên đường thẳng AH có phương trình là : \[2(x + 1) + 3(y - 2) = 0 \Rightarrow 2x + 3y - 4 = 0\]

Ta có \[\overrightarrow {AC}  = (5;4)\] là vectơ pháp tuyến của đường thẳng BH nên đường thẳng BH có phương trình là : \[5(x - 2) + 4(y - 3) = 0 \Leftrightarrow 5x + 4y - 22 = 0\]

Suy ra toạ độ điểm H là nghiệm của hệ phương trình sau :

\[\left\{ {\begin{array}{*{20}{c}}{2x + 3y - 4 = 0}\\{5x + 4y - 22 = 0}\end{array} \Rightarrow H = \left( {\frac{{50}}{7}; - \frac{{24}}{7}} \right)} \right.\]

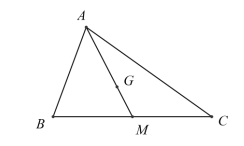
Ví dụ 4. Cho tam giác ABC có đỉnh C(-2; -4) và trọng tâm G(0;4). Hãy viết phương trình đường thẳng AB biết rằng M(2;2) là trung điểm của cạnh BC.

Lời giải

Vì M(2;2) là trung điểm của cạnh BC nên ta có:

\[\left\{ {\begin{array}{*{20}{c}}{\frac{{{x_B} + ( - 2)}}{2} = 2}\\{\frac{{{y_B} + ( - 4)}}{2} = 2}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{{x_B} = 2.2 + 2 = 6}\\{{y_B} = 2.2 + 4 = 8}\end{array}} \right. \Rightarrow B = \left( {6;8} \right)} \right.\]

Vì G là trọng tâm tam giác ABC nên \[\overrightarrow {AG}  = 2\overrightarrow {GM} \]

\[ \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{0 - {x_A} = 2(2 - 0)}\\{4 - {y_A} = 2(2 - 4)}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{{x_A} =  - 4}\\{{y_A} = 8}\end{array} \Rightarrow } \right.A = \left( { - 4;8} \right)\]

Ta có: \[\overrightarrow {AB}  = (10;1)\]nên vectơ pháp tuyến của đường thẳng AB là: \[\overrightarrow {{n_{AB}}}  = (0;1)\]

Phương trình đường thẳng AB là: \[0(x + 4) + 1(y - 8) = 0 \Leftrightarrow y - 8 = 0\]

Ví dụ 5. Cho đường thẳng d có hệ số góc bằng -3 và A(1;2) nằm trên d.

a. Lập phương trình tham số của đường thẳng d;

b. Lập phương trình tổng quát của đường thẳng d.

Lời giải

a. Đường thẳng d có hệ số góc bằng -3 nên có vectơ chỉ phương là (1;-3).

Đường thẳng d đi qua điểm A(1;2) và có vectơ chỉ phương là (1;-3) nên có phương trình tham số là : \[\left\{ {\begin{array}{*{20}{c}}{x = 1 + t}\\{y = 2 - 3t}\end{array}} \right.\]

b. Đường thẳng d có hệ số góc bằng -3 nên có vectơ pháp tuyến là (3;1).

Đường thẳng d đi qua điểm A(1;2) và có vectơ pháp tuyến là (3;1) nên có phương trình tổng quát là : \[3(x - 1) + 1(y - 2) = 0 \Leftrightarrow 3x + y - 5 = 0\]

Ví dụ 6. Hãy viết phương trình tổng quát của đường thẳng d đi qua A(2;-5) và nó tạo với trục Ox một góc 60⁰

Lời giải

Hệ số góc của đường thẳng d là \[k = \tan {60^0} = \frac{{\sqrt 3 }}{3}\].

Phương trình đường thẳng d là :

\[y = \frac{{\sqrt 3 }}{3}(x - 2) - 5 \Leftrightarrow \sqrt 3 x - 3y - 15 - 2\sqrt 3  = 0\]

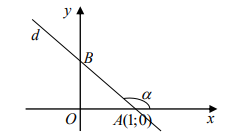
Ví dụ 7. Cho đường thẳng d cắt trục Ox, Oy lần lượt tại A, B. Biết rằng A(1;0) và BAO 45⁰ . Hãy viết phương trình đường thẳng d.

Lời giải

Gọi a là góc giữa đường thẳng d và trục Ox.

Trường hợp 1 :

BAO + a = 180⁰ Þ a = 180⁰ – 45⁰ = 135⁰

Suy ra hệ số góc của đường thẳng d là: k tan135⁰ = -1.

Đường thẳng d có hệ số góc k = -1 và đi qua A(1;0) nên có phương trình là:

\[y =  - 1(x - 1) + 0 \Leftrightarrow x + y - 1 = 0\]

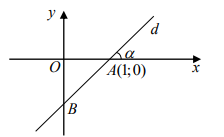
Trường hợp 2 : BAO = a Þ a = 45⁰

Suy ra hệ số góc của đường thẳng d là : k = tan 45⁰ = 1.

Đường thẳng d có hệ số góc k =1 và đi qua A(1;2) nên có phương trình đường thẳng d là : \[y = 1(x - 1) + 0 \Leftrightarrow x - y - 1 = 0\]

Ví dụ 8. Đường thẳng d đi qua M(-1; -5) cắt trục Ox, Oy lần lượt tại A, B sao cho OA = 2OB. Hãy viết phương trình đường thẳng d.

Lời giải

Cách 1 : Sử dụng phương trình đường thẳng dạng hệ số góc.

Gọi a là góc giữa đường thẳng d và trục Ox.

Do tam giác OAB vuông tại O nên ta có: \[\tan BAO = \frac{{OB}}{{OA}} = \frac{1}{2}\]

Trường hợp 1 : BAO + a = 180⁰

Þ \[\tan \alpha  =  - \frac{1}{2}\].

Đường thẳng d có hệ số góc bằng \[ - \frac{1}{2}\]và đi qua M(-1; -5) nên có phương trình là : \[y =  - \frac{1}{2}(x + 1) - 5 \Leftrightarrow x + 2y + 11 = 0\]

Trường hợp 2 : BAO = a Þ \[\tan \alpha  = \frac{1}{2}\]. Đường thẳng d có hệ số góc bằng \[\frac{1}{2}\] và đi qua M(-1; -5) nên có phương trình là : \[y = \frac{1}{2}(x + 1) - 5 \Leftrightarrow x - 2y - 9 = 0\]