Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu 40 câu trắc nghiệm max min hàm số chứa dấu giá trị tuyệt đối, tài liệu bao gồm 24 trang, 40 câu trắc nghiệm và có đáp án chi tiết. Tài liệu được tổng hợp từ các tài liệu ôn thi hay nhất  giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kỳ thi sắp hới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây

40 câu trắc nghiệm max min hàm số chứa dấu giá trị tuyệt đối - có đáp án chi tiết

Câu 1. Có bao nhiêu giá trị nguyên của x để hàm số \[y = \left| {x - 1} \right| + \left| {x + 3} \right|\] đạt giá trị nhỏ nhất.

A. 4 .

B. 5 .

C. 2 .

D. 3 .

Lời giải: Chọn B

Ta có \[y = \left| {x - 1} \right| + \left| {x + 3} \right| = \left\{ {\begin{array}{*{20}{c}}{2x + 2,x \ge 1}\\{4, - 3 \le x \le 1}\\{ - 2x - 2,x <  - 3}\end{array}} \right.\].

Trên 1; \[ + \infty \], ta có \[y \ge 4\] và dấu bằng xảy ra khi x = 1.

Trên –3;1 , ta có y = 4 và có bốn giá trị nguyên của x thuộc khoảng này.

Trên \[ - \infty \]; – 3 , ta có y = –2x – 2 > 4 .

Vậy y_min = 4 và có 5 giá trị nguyên của x để y_min = 4 .

Câu 2. Cho hàm số \[f(x) = \left| {x - 1} \right| + \left| {x + 2} \right| + \left| {x + 5} \right| + \left| {x - 10} \right|\] và hàm số \[g(x) = \left| {{x^3} - 3x + m - 1} \right|\]. Khi hàm số \[f(x)\]đạt giá trị nhỏ nhất thì \[g(x)\] đạt giá lớn nhất bằng 8 . Hỏi tổng tất cả các giá trị tuyệt đối của tham số thực m thỏa mãn bài toán bằng bao nhiêu?

A. 12

B. 2

C. 8

D. 7

Lời giải: Chọn A

Xét hàm số

 \[\begin{array}{l}f(x) = \left| {x - 1} \right| + \left| {x + 2} \right| + \left| {x + 5} \right| + \left| {x - 10} \right|\\ = \left| {x - 1} \right| + \left| { - 2 - x} \right| + \left| { - 5 - x} \right| + \left| {x + 10} \right|\end{array}\]

\[ \ge \left| {(x - 1) + ( - 2 - x) + ( - 5 - x) + (x - 10)} \right| = 4\], dấu bằng xảy ra khi  \[x - 1; - 2 - x; - 5 - x;x - 10\] có cùng dấu hay - 2 £ x £ 1.

Vậy yêu cầu bài toán là hàm số

\[g(x) = \left| {{x^3} - 3x + m - 1} \right|\] đạt giá trị lớn nhất bằng 8 với -2 £ x £ 1.

Lập bảng biến thiên, suy ra các trường hợp sau:

Th1: m - 3 ³ 0. Khi đó, \[\mathop {\max }\limits_{x \in [ - 2;1]} \left| {g(x)} \right| = g( - 1) = m + 1 = 8\] hay m = 7 .

Th2: m - 3 < 0 < m + 1. Khi đó,

\[\mathop {\max }\limits_{x \in [ - 2;1]} \left| {g(x)} \right| = \max \left\{ {\left| {g( - 1)} \right|,\left| {g( - 2)} \right| = \left| {g(1)} \right|} \right\} = \max \left\{ {3 - m,m + 1} \right\} = 8\]

Th3: m + 1 £ 0.

Khi đó, \[\mathop {\max }\limits_{x \in [ - 2;1]} \left| {g(x)} \right| = \left| {g( - 1)} \right| = \left| {g(1)} \right| = 3 - m = 8\] hay m =-5.

Câu 3. Giá trị nhỏ nhất của hàm số \[y = \left| {2x - 1} \right| + \left| {3x + 2} \right| + \left| {7x - 4} \right|\] là \[\frac{a}{b}\] với a, b nguyên dương, phân số \[\frac{a}{b}\] tối giản. Khi đó a + b bằng

A. 5 .

B. 34 .

C. 12.

D. 41.

Lời giải: Chọn B

Ta có

\[\begin{array}{l}y = \left| {2x - 1} \right| + \left| {3x + 2} \right| + \left| {7x - 4} \right|\\ = \left\{ {\begin{array}{*{20}{c}}{3 - 12x;khi <  - \frac{2}{3}}\\{7 - 6x;khi - \frac{2}{3} \le x < \frac{1}{2}}\\{5 - 2x;khi\frac{1}{2} \le x < \frac{4}{7}}\\{12x - 3;khix \ge \frac{4}{7}}\end{array}} \right.\end{array}\]

BBT:

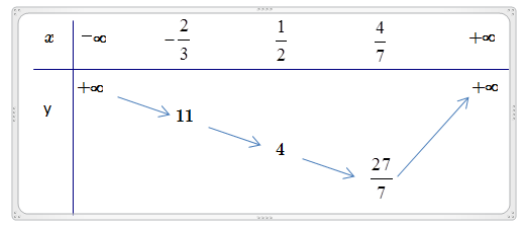
Từ BBT suy ra giá trị nhỏ nhất của hàm số là

\[\frac{{27}}{7} = \frac{a}{b} \Rightarrow \left\{ {\begin{array}{*{20}{c}}{a = 27}\\{b = 7}\end{array} \Rightarrow a + b = 34} \right.\]

Câu 4. Giá trị nhỏ nhất của hàm số \[y = \left| {\sqrt {4 - {x^2}}  - 9} \right|\] trên đoạn [-2;2] bằng

A. 0 .

B. 6 .

C. 7 .

D. 9 .

Lời giải: Chọn C

Xét hàm số \[y = f(x) = \left| {\sqrt {4 - {x^2}}  - 9} \right|\], có \[y' = \frac{{ - x}}{{\sqrt {4 - {x^2}} }} = 0 \Rightarrow x = 0\].

Ta có bảng biến thiên của hàm số \[y = f(x)\] và \[y = \left| {f(x)} \right|\] trên [-2;2] như sau:

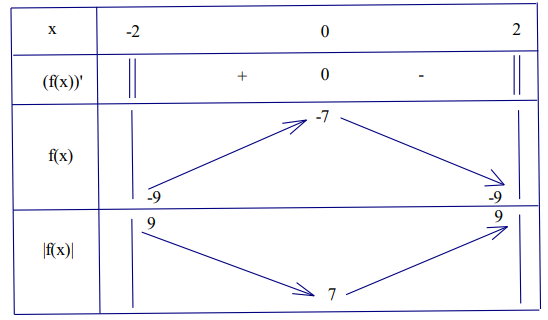
Từ đó ta có giá trị nhỏ nhất của hàm số \[y = \left| {\sqrt {4 - {x^2}}  - 9} \right|\]trên [-2;2] là 7 khi x = 0 .

Câu 5. Cho hàm số \[y = f(x) = \left| {{x^4} - 4{x^3} + 4{x^2} + a} \right|\]. Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn [0;2] . Có bao nhiêu số nguyên a thuộc đoạn [-3;2] sao cho M £ 2m ?

A. 7.

B. 5.

C. 6.

D. 4.

Lời giải: Chọn D

Đặt

\[\begin{array}{l}g(x) = {x^4} - 4{x^3} + 4{x^2} + a\\ \Rightarrow g'(x) = 4{x^3} - 12{x^2} + 8x = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = 0}\\{x = 1}\\{x = 2}\end{array}} \right.\end{array}\].

Ta có g(0) = a; g(1) = a + 1; g(2) = a.

\[\alpha  = \mathop {\max }\limits_{x \in [0;2]} g(x) = \max \left\{ {g(0);g(1);g(2)} \right\} = a + 1\].

\[\beta  = \mathop {\min }\limits_{x \in [0;2]} g(x) = \min \left\{ {g(0);g(1);g(2)} \right\} = a\].

Trường hợp 1: \[a > 0 \Rightarrow \left\{ {\begin{array}{*{20}{c}}{M = a + 1}\\{m = a}\end{array}} \right.\].

Khi đó

\[\begin{array}{l}M \le 2m \Leftrightarrow a + 1 \le 2a\\ \Leftrightarrow a \ge 1,a \in [ - 3;2] \Rightarrow a \in \{ 1;2\} \end{array}\].

Trường hợp 2: \[a + 1 < 0 \Leftrightarrow a <  - 1 \Rightarrow \left\{ {\begin{array}{*{20}{c}}{M =  - a}\\{m =  - a - 1}\end{array}} \right.\].

Khi đó

\[\begin{array}{l}M \le 2m \Leftrightarrow  - a \le  - 2a - 2\\ \Leftrightarrow a \le  - 2,a \in [ - 3;2] \Rightarrow a \in \{  - 3; - 2\} \end{array}\].

Trường hợp 3: \[a(a + 1) \le 0 \Leftrightarrow  - 1 \le a \le 0\]

Khi đó

\[\begin{array}{l}M = \max \left\{ {\left| {a + 1} \right|,\left| a \right|} \right\} = \max \left\{ {\left| {a + 1} \right|,\left| { - a} \right|} \right\}\\ \ge \frac{{\left| {a + 1} \right| + \left| { - a} \right|}}{2} \ge \frac{{\left| {a + 1 - a} \right|}}{2} = \frac{1}{2} > 0 = m\end{array}\].

Như vậy có tất cả 4 giá trị của a thỏa mãn yêu cầu.

Câu 6. Có bao nhiêu giá trị thực của tham số m để giá trị lớn nhất của hàm số \[f(x) = \left| {{x^2} + 2x + m - 4} \right|\]trên đoạn [-2;1] bằng 5 ?

A. 2 .

B. 1.

C. 3 .

D. 4 .

Lời giải: Chọn A

Đặt \[t = {x^2} + 2x - 4,x \in [ - 2;1] \Rightarrow t \in [ - 5; - 1]\]

Ta có: \[y = \left| {t + m} \right|\]

\[\begin{array}{l} \Rightarrow {y_{\max }} = \max \left\{ {\left| {m - 1} \right|;\left| {m - 5} \right|} \right\} = 5\\ \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{\left\{ {\begin{array}{*{20}{c}}{\left| {m - 1} \right| = 5}\\{\left| {m - 1} \right| \ge \left| {m - 5} \right|}\end{array}} \right.}\\{\left\{ {\begin{array}{*{20}{c}}{\left| {m - 5} \right| = 5}\\{\left| {m - 1} \right| < \left| {m - 5} \right|}\end{array}} \right.}\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{m = 6}\\{m = 0}\end{array}} \right.\end{array}\]

Câu 7. Có bao nhiêu số nguyên m để giá trị nhỏ nhất của hàm số \[y = \left| {{x^4} - 38{x^2} + 120x + 4m} \right|\]trên đoạn [0;2] đạt giá trị nhỏ nhất.

A. 26.

B. 13.

C. 14.

D. 27.

Lời giải: Chọn D

Xét \[u = {x^4} - 38{x^2} + 120x + 4m\] trên đoạn [0;2] ta có \[u' = 0 \Leftrightarrow 4{x^3} - 76x + 120 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x =  - 5}\\{x = 2}\\{x = 3}\end{array}} \right.\]

Vậy \[\left\{ {\begin{array}{*{20}{c}}{\mathop {\max }\limits_{[0;2]} u = \max \left\{ {u(0),u(2)} \right\} = \max \left\{ {4m,4m + 104} \right\} = 4m + 104}\\{\mathop {\min }\limits_{[0;2]} u = \min \left\{ {u(0),u(2)} \right\} = \min \left\{ {4m,4m + 104} \right\} = 4m}\end{array}} \right.\]

Khi đó

\[\begin{array}{l}\min \left\{ {\mathop {\min }\limits_{[0;2]} y} \right\} = 0 \Leftrightarrow 4m(4m + 104) \le 0\\ \Leftrightarrow  - 26 \le m \le 0\end{array}\]

Có 27 số nguyên thỏa mãn.

Chú ý ôn tập lại kiến thức đã học

Giá trị lớn nhất và giá trị nhỏ nhất của hàm số \[y = \left| {u(x)} \right|\] và \[u = {\left( {u(x)} \right)^{2n}}\].

Gọi \[m = \mathop {\min }\limits_{[a;b]} u(x);M = \mathop {\max }\limits_{[a;b]} u(x)\].

Khi đó \[\mathop {\max }\limits_{[a;b]} y\]   \[\mathop {\max }\limits_{[a;b]} \left\{ {\left| M \right|,\left| m \right|} \right\}\]   \[\frac{{\left| M \right|\left| m \right|\left| {\left| M \right|\left| m \right|} \right|}}{2}\]

Giá trị nhỏ nhất không có công thức nhanh mà phụ thuộc và dấu của M và m

\[m \ge 0 \Rightarrow \mathop {\min }\limits_{[a;b]} y = m\]

\[M \le 0 \Rightarrow \mathop {\min }\limits_{[a;b]} y =  - m\]

\[m.M < 0 \Rightarrow \exists {x_0} \in (a;b)|y({x_0}) = 0 \Rightarrow \mathop {\min }\limits_{[a;b]} y = 0\]

Câu 8. Cho hàm số \[f(x) = \left| {2{x^3} - 3{x^2} + m} \right|\]có bao nhiêu số nguyên m để \[\mathop {\min }\limits_{[ - 1;3]} f(x) \le 3\]

A. 4

B. 8

C. 31

D. 39

Lời giải: Chọn D

Xét \[t = 2{x^3} - 3{x^2} + m \Rightarrow 6{x^2} - 6x = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = 0}\\{x = 1}\end{array}} \right.\].

Do đó: \[\mathop {\min }\limits_{[ - 1;3]} t(x) = m - 5;\mathop {\max }\limits_{[ - 1;3]} t(x) = m + 27\].

Nếu \[m - 5 \ge 0 \Rightarrow \mathop {\min }\limits_{[ - 1;3]} f(x) = m - 5 \le 3\]

\[ \Leftrightarrow 5 \le m \le 8 \Rightarrow m \in \{ 5;6;7;8\} \].

Nếu

\[\begin{array}{l}m + 27 \le 0 \Rightarrow \mathop {\min }\limits_{[ - 1;3]} f(x) =  - (m + 27) \le 3\\ \Leftrightarrow  - 30 \le m \le  - 27\\ \Rightarrow m \in \{  - 30; - 29; - 28; - 27\} \end{array}\]

Nếu \[(m - 5)(m + 27) \le 0 \Rightarrow \mathop {\min }\limits_{[ - 1;3]} f(x) = 0\]

Vậy, \[m \in \{  - 30; - 29;...;8\} \]có tất cả 39 số nguyên thỏa mãn.

Câu 9: Có bao nhiêu giá trị nguyên của tham số m để \[\mathop {\max }\limits_{[0;3]} \left| {{x^2} - 2x + m} \right| \le 5\]?

A. 5

B. 6

C. 7

D. 8

Lời giải: Chọn B

Đặt \[f(x) = {x^2} - 2x + m\] là hàm số xác định và liên tục trên đoạn [0;3].

Ta có . \[f'(x) = 2x - 2\] . Với mọi \[x \in [0;3]\] ta có

 \[f'(x) = 0 \Leftrightarrow 2x - 2 = 0 \Leftrightarrow x = 1\].

Mặt khác: \[\begin{array}{l}f(0) = m\\f(1) = m - 1\\f(3) = m + 3\end{array}\]

Ta có: \[\mathop {\max }\limits_{[0;3]} \left| {f(x)} \right| = \max \left\{ {\left| {f(0)} \right|;\left| {f(1)} \right|;\left| {f(3)} \right|} \right\}.\]

Theo bài: \[\mathop {\max }\limits_{[0;3]} \left| {f(x)} \right| \le 5 \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{\left| {f(0)} \right| \le 5}\\{\left| {f(1)} \right| \le 5}\\{\left| {f(3)} \right| \le 5}\end{array}} \right.\]

\[ \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{\left| m \right| \le 5}\\{\left| {m - 1} \right| \le 5}\\{\left| {m + 3} \right| \le 5}\end{array} \Leftrightarrow } \right.\left\{ {\begin{array}{*{20}{c}}{ - 5 \le m \le 5}\\{ - 5 \le m - 1 \le 5}\\{ - 5 \le m + 3 \le 5}\end{array}} \right.\]

\[ \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{ - 5 \le m \le 5}\\{ - 4 \le m \le 6}\\{ - 8 \le m \le 2}\end{array} \Leftrightarrow  - 4 \le m \le 2} \right.\].

Do \[m \in Z \Rightarrow m \in S = \{  - 4; - 3; - 2; - 1;0;1\} \].

Vậy có tất cả 6 giá trị của m thỏa mãn yêu cầu bài toán.

Câu 10. Có bao nhiêu giá trị nguyên của tham số để giá trị lớn nhất của hàm số \[f(x) = \left| {{x^2} - 2x + m} \right|\] trên đoạn [0;3] không lớn hơn 3?

A. 4

B. 5

C. 6

D. 3

Lời giải: Chọn D

Xét hàm số \[g(x) = {x^2} - 2x + m\]liên tục trên đoạn [0;3] có \[g'(x) = 2x - 2 = 0 \Leftrightarrow x = 1\].

\[\begin{array}{l}\mathop {Max}\limits_{[0;3]} f(x) = Max\left\{ {\left| {g(0)} \right|,\left| {g(3)} \right|,\left| {g(1)} \right|} \right\}\\ = Max\left\{ {\left| m \right|,\left| {m + 3} \right|,\left| {m - 1} \right|} \right\}\\ = Max\left\{ {\left| {m + 3} \right|,\left| {m - 1} \right|} \right\}.\end{array}\]

\[\begin{array}{l}\mathop {Max}\limits_{[0;3]} f(x) \le 3 \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{\left| {m + 3} \right| \le 3}\\{\left| {m - 1} \right| \le 3}\end{array}} \right.\\ \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{ - 3 \le m + 3 \le 3}\\{ - 3 \le m - 1 \le 3}\end{array}} \right. \Leftrightarrow  - 2 \le m \le 0.\end{array}\]

Các giá trị nguyên thỏa mãn yêu cầu bài toán của tham số m là -2, -1, 0.

Câu 11. Có bao nhiêu số nguyên \[m \in  - 5;5\]để \[\mathop {\min }\limits_{1;3} \left| {{x^3} - 3{x^2} + m} \right| \ge 2\]

A. 6

B. 4

C. 3

D. 5

Lời giải: Chọn B

Ta có

\[\begin{array}{l}\mathop {\min }\limits_{1;3} \left| {{x^3} - 3{x^2} + m} \right| \ge 2\\ \Leftrightarrow \left| {{x^3} - 3{x^2} + m} \right| \ge 2;\forall x \in 1;3\end{array}\]   (1)

Giải (1): \[\left| {{x^3} - 3{x^2} + m} \right| \ge 2;\forall x \in 1;3\]

\[ \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{{x^3} - 3{x^2} + m \ge 2;\forall x \in 1;3}\\{{x^3} - 3{x^2} + m \le  - 2;\forall x \in 1;3}\end{array}} \right.\]

\[ \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{{x^3} - 3{x^2} \ge 2 - m;\forall x \in 1;3}\\{{x^3} - 3{x^2} \le  - 2 - m;\forall x \in 1;3}\end{array}} \right.\]

\[ \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{2 - m \le \mathop {\min }\limits_{1;3} {x^3} - 3{x^2}}\\{ - 2 - m \ge \mathop {\max }\limits_{1;3} {x^3} - 3{x^2}}\end{array}} \right.\] (*)

Xét hàm số \[f(x) = {x^3} - 3{x^2}\] trên 1;3. Hàm số xác định và liên tục trên 1;3 mà \[f'(x) = 3{x^2} - 6x = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = 0}\\{x = 2}\end{array}} \right.\].

Ta có \[f(1) =  - 2;f(3) = 0;f(2) =  - 4\].

Do đó \[\mathop {\max }\limits_{1;3} f(x) = 0;\mathop {\min }\limits_{1;3} f(x) =  - 4\].

 Từ (*) suy ra \[\left[ {\begin{array}{*{20}{c}}{2 - m \le  - 4}\\{ - 2 - m \ge 0}\end{array} \Leftrightarrow } \right.\left[ {\begin{array}{*{20}{c}}{m \ge 6}\\{m \le  - 2}\end{array}} \right.\].

Vì \[\left\{ {\begin{array}{*{20}{c}}{m \in  - 5;5}\\{m \in Z}\end{array}} \right.\] nên \[m \in \{  - 5; - 4; - 3; - 2\} \].

Vậy m có 4 giá trị m thỏa mãn yêu cầu bài toán.

Cách 2:

Đặt \[t = {x^3} - 3{x^2}\], với \[x \in 1;3 \Rightarrow t \in  - 4;0\]. Khi đó bài toán trở thành \[\mathop {\min }\limits_{ - 4;0} \left| {t + m} \right| \ge 2\].

TH1:

\[\begin{array}{l} - m \le  - 4 \Rightarrow \mathop {\min }\limits_{ - 4;0} \left| {t + m} \right| = \left| { - 4 + m} \right|\\ = m - 4 \ge 2 \Leftrightarrow m \ge 6\end{array}\].

TH2: \[ - m \ge 0 \Rightarrow \mathop {\min }\limits_{ - 4;0} \left| {t + m} \right| = \left| m \right| =  - m \ge 2 \Leftrightarrow m \le  - 2\].

Kết hợp với điều kiện \[\left\{ {\begin{array}{*{20}{c}}{m \in  - 5;5}\\{m \in Z}\end{array}} \right.\]suy ra \[m \in \{  - 5; - 4; - 3; - 2\} \].

Vậy có 4 giá trị m thỏa mãn yêu cầu bài toán.