Tailieumoi.vn xin giới thiệu Bài tập Toán 9 Chương 3 Bài 9:Độ dài đường tròn, cung tròn . Bài viết gồm 50 bài tập với đầy đủ các mức độ và có hướng dẫn giải chi tiết sẽ giúp học sinh ôn luyện kiến thức và rèn luyện kĩ năng làm bài tập Toán 9. Ngoài ra, bài viết còn có phần tóm tắt nội dung chính lý thuyết Chương 3 Bài 9: Độ dài đường tròn, cung tròn. Mời các bạn đón xem:
Bài tập Toán 9 Chương 3 Bài 9: Độ dài đường tròn, cung tròn
A. Bài tập Độ dài đường tròn, cung tròn
I. Bài tập trắc nghiệm
Câu 1: Số đo n° của cung tròn có độ dài 30,8 cm trên đường tròn có bán kính 22 cm là (lấy π ≃ 3,14 và làm tròn đên độ)
A. 70°
B. 80°
C. 65°
D. 85°
Lời giải:
Độ dài cung tròn
Chọn đáp án B
Câu 2: Tính độ dài cung 30° của một đường tròn có bán kính 4 dm
Lời giải:
Độ dài cung
Chọn đáp án D
Câu 3: Chu vi đường tròn bán kính R = 9 là
A. 18π
B. 9π
C. 12π
D. 27π
Chu vi C = 2πR = 2π.9 = 18π
Chọn đáp án A
Câu 4: Biết chu vi đường tròn là C = 36π (cm) . Tính đường kính của đường tròn.
A. 18(cm)
B. 14(cm)
C. 36(cm)
D. 20(cm)
Chu vi C = πd = 36π ⇒ d = 36.36π .
Vậy đường kính cần tìm là 36cm
Chọn đáp án C.
Câu 5: Cho đường tròn tâm O có chu vi 36π cm. Tính độ dài cung có số đo 90°?
A. 9π
B. 4,5π
C. 18π
D. 15π
Chọn đáp án A
Câu 6: Biết độ dài cung 60° là 6π. Tính độ dài cung tròn có số đo 100°.
A. 6π
B. 8π
C. 10π
D. 10,5π
Lời giải:
Chọn đáp án C.
Câu 7: Cho tam giác ABC có AB= 8cm; AC = 6cm và BC = 10cm. Tính chu vi đường tròn ngoại tiếp tam giác ABC?
A. 8π (cm)
B. 10π (cm)
C. 6π (cm)
D. 12π (cm)
Ta có: AB2 + AC2 = BC2 ( = 100)
Suy ra, tam giác ABC là tam giác vuông tại
A. Do đó, tâm đường tròn ngoại tiếp tam giác ABC là trung điểm M của BC.
Bán kính đường tròn là: R = BC/2 = 5cm
Chu vi đường tròn ngoại tiếp tam giác ABC là:
C = 2π.5 = 10π (cm)
Chọn đáp án B.
Câu 8: Cho hình vuông ABCD có độ dài cạnh là 10 cm . Gọi O là tâm đường tròn nội tiếp hình vuông. Gọi M, N lần lượt là trung điểm của AB; BC. Tính độ dài của cung MN⌢ ?
A. 2π (cm)
B. 5π (cm)
C. 2,5π (cm)
D. 7,5π (cm)
Do O là tâm đường tròn nội tiếp hình vuông ABCD nên bán kính đường tròn nội tiếp hình vuông là:
Chọn đáp án C.
Câu 9: Biết độ dài cung 60° bằng 6π (cm). Tính bán kính đường tròn
A. R =10 cm
B. R = 8cm
C. R =12cm
D. R = 18cm
Độ dài cung 60° là:
Chọn đáp án D.
Câu 10: Cho đường tròn (O; R), độ dài cung có số đo n° là 0,314. R.Tính n?
A. 18°
B. 20°
C. 36°
D. 30°
Độ dài cung có số đo n° là:
Chọn đáp án A.
Câu 11: Cho tam giác ABC vuông tại A, cạnh AB = 5cm, 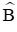
+) Xét đường tròn (I) đường kính AB có 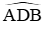
+) Gọi K là trung điểm của AC ⇒ KA = KC = KD ⇒ D thuộc đường tròn đường kính AC ⇒ Phương án C đúng
+) Ta có ∆IBD cân tại I có 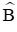
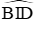
Đáp án cần chọn là: A
Câu 12: Cho tam giác ABC vuông tại A, cạnh AB = 4cm, 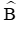
+) Xét tam giác ABC vuông tại A có 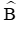
+) Vì AC ⊥ AB và A ∈ 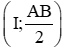
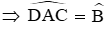
+) Vì 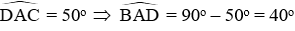
Độ dài cung nhỏ BD của (I) là 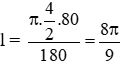
+) Số đo cung lớn BD là 360o – 80o = 280o
Độ dài cung lớn BD của (I) là 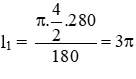
Đáp án cần chọn là: D
*Chú ý: Độ dài cung lớn BD các em có thể tính bằng cách lấy chu vi đường tròn trừ đi độ dài cung nhỏ BD
Câu 13: Cho tam giác ABC có AB = AC = 3cm, Â = 120o. Tính độ dài đường tròn ngoại tiếp tam giác ABC
A. 12π
B. 9π
C. 6π
D. 3π
Gọi O là tâm đường tròn ngoại tiếp tam giác ABC. Vì tam giác ABC cân tại A nên AO vừa là đường cao vừa là đường phân giác của
⇒ ∆CAO đều nên OA = OC = AC = 3cm
Nên bán kính đường tròn ngoại tiếp ∆ABC là R = 3cm
Chu vi đường tròn (O) là C = 2πR = 6π (cm)
Đáp án cần chọn là: C
Câu 14: Cho tam giác ABC có AB = AC = 4cm, Â = 100o. Tính độ dài đường tròn ngoại tiếp tam giác ABC
A. 6,22π
B. 3,11π
C. 6π
D. 12,44π
Gọi O là tâm đường tròn ngoại tiếp tam giác ABC. Vì tam giác ABC cân tại A nên AO vừa là đường cao vừa là đường phân giác của
Xét tam giác OAC cân tại O (vì OA = (C) có:
Nên bán kính đường tròn ngoại tiếp ∆ABC là R ≈ 3,11cm
Chu vi đường tròn (O) là C = 2πR ≈ 6,22 (cm)
Đáp án cần chọn là: A
Câu 15: Chu vi đường tròn ngoại tiếp tam giác đều cạnh a (cm) là:
Lời giải:
Gọi O là tâm đường tròn ngoại tiếp tam giác đều ABC, suy ra O cũng là trọng tâm của tam giác ABC
Tia CO ⊥ AB tại D thì D là trung điểm của AB
Nên bán kính đường tròn ngoại tiếp tam giác ABC là
Đáp án cần chọn là: B
II. Bài tập tự luận có lời giải
Câu 1: Cho đường tròn (O), bán kính R = 4cm. Tính chu vi của đường tròn ?
Lời giải:
Chu vi của đường tròn là:
C = 2πR = 2π.4 = 8π (cm)
Câu 2: Tính chu vi của hình tròn có độ dài cung có số đo 60° là 10π (cm)
Lời giải:
Gọi R là bán kính của hình tròn
Theo đề bài ta có:
III. Bài tập vận dụng
Câu 1: Xích Đạo là một đường tròn lớn của Trái Đất có độ dài khoảng 40000km. Hãy tính bán kính của Trái Đất.
Câu 2: Máy cày có hai bánh xe sau lớn hơn hai bánh xe trước. Biết khi bơm căng, bánh xe trước có đường kính 0,8m, bánh xe sau có đường kính 1,5m. Hỏi bánh xe sau lăn được 16 vòng thì bánh xe trước lăn được mấy vòng?
B. Lý thuyết Độ dài đường tròn, cung tròn
1. Công thức tính độ dài đường tròn
“Độ dài đường tròn” hay còn được gọi là “chu vi đường tròn” được kí hiệu là C.
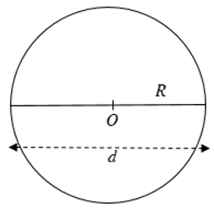
Công thức tính chu vi hình tròn: C = 2πR hoặc C = πd.
Trong đó: C là độ dài đường tròn;
R là bán kính đường tròn;
d là đường kính của đường tròn;
π (đọc là “pi”) là kí hiệu của một số vô tỉ mà giá trị gần đúng thường được lấy là π ≈ 3,14.
Ví dụ 1. Cho đường tròn có bán kính 5 cm. Tính độ dài đường tròn đó?
Lời giải:
Độ dài đường tròn là:
C = 2πR = 2π . 5 = 10π (cm).
Vậy đường tròn có bán kính R = 5 cm có độ dài đường tròn là 10π cm.
2. Công thức tính độ dài cung tròn
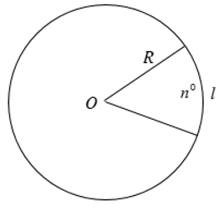

Ví dụ 2. Cho đường tròn có bán kính 4cm. Tính độ dài cung tròn 120o.
Lời giải:
Độ dài cung tròn 120o là:
(cm)
Vậy độ dài cung tròn 120o của đường tròn (O; 4cm) là cm.





