Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu Phương pháp giải bài toán về mặt cầu ngoại tiếp hình chóp, tài liệu bao gồm 9 trang. Tài liệu được tổng hợp từ các tài liệu ôn thi hay nhất  giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kỳ thi sắp hới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây

Phương pháp giải bài toán về mặt cầu ngoại tiếp hình chóp

Nội dung gồm có

A.LỜI MỞ ĐẦU  

B. NỘI DUNG

I. Cơ sở lí thuyết.

II. Các phương pháp xác định tâm mặt cầu ngoại tiếp hình chóp.

III. Cách xác định tâm và tính bán kính mặt cầu ngoại tiếp của một số hình chóp đặc biệt

IV. Các ví dụ minh họa

PHƯƠNG PHÁP GIẢI BÀI TOÁN MẶT CẦU NGOẠI TIẾP HÌNH CHÓP.

A. LỜI MỞ ĐẦU

Bài toán mặt cầu ngoại tiếp hình chóp xuất hiện nhiều trong các đề kiểm tra, các đề thi vào đại học. Qua thực tế giảng dạy chúng tôi thấy rằng: Nhiều học sinh tỏ ra lúng túng khi gặp các bài toán có liên quan đến mặt cầu. Bài viết này cùng trao đổi với các em và bạn đồng nghiệp một vài kỹ thuật giải toán thông qua các ví dụ về mặt cầu ngoại tiếp hình chóp.Các vấn đề thường gặp liên quan đến bài toán mặt cầu ngoại tiếp hình chóp kiểu như:Chứng minh các điểm nào đó cùng nằm trên một mặt cầu? Xác định tâm và tính bán kính mặt cầu ngoại tiếp hình chóp? Hay tính diện tích mặt cầu ngoại tiếp hình chóp hay thể tích khối cầu ngoại tiếp khối chóp?....

B. NỘI DUNG

I. Cơ sở lí thuyết.

Định lí:

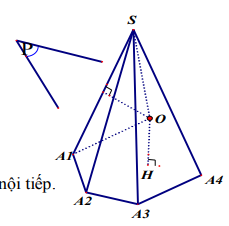
 Điều kiện cần và đủ để hình chóp SA₁A₂…An có mặt cầu ngoại tiếp là đa giác đáy A₁A₂…A_n phải là đa giác nội tiếp.

Chứng minh:

1.Điều kiện cần:

Giả sử tồn tại mặt cầu tâm O ngoại tiếp hình chóp SA₁A₂…A_n , tức là ta có

OS = OA₁ = OA₂ =…= OA_n      (1)

Kẻ OH vuông góc mặt phẳng đáy (A₁A₂…A_n )

 Þ HA₁ = HA₂ =…= HA_n (2)

Đẳng thức (2) chứng tỏ đáy A₁A₂…A_n là một đa giác nội tiếp

2. Điều kiện đủ

Giả sử A₁A₂…A_n là một đa giác nội tiếp. Gọi H là tâm đường tròn ngoại tiếp đáy. Qua H dựng đường thẳng \(\Delta \) vuông góc (A₁A₂…A_n ). Vẽ mặt phẳng trưng trực (P) của một cạnh bất kì của hình chóp ( chẳng hạn cạnh SA₁).

Do \(\Delta \) không song song (P) nên giả sử \(\Delta  \cap \left( P \right) = O\)

Khi đó ta thấy OA₁ = OA₂ =…= OA_n, OA₁ = OS.

Từ đó suy ra O là tâm mặt cầu ngoại tiếp hình chóp đa giác SA₁A₂…A_n .

Chú ý: Từ định lí trên ta rút ra các kết luận sau:

Nói riêng mọi hình chóp tam giác (tứ diện), mọi hình chóp đều, đều có mặt cầu ngoại tiếp

II. Các phương pháp xác định tâm mặt cầu ngoại tiếp hình chóp.

Bài toán: Xác định tâm I và tính bán kính R của mặt cầu ngoại tiếp hình chóp SA₁A₂…A_n.

Phương pháp 1: Gọi I là tâm mặt cầu ngoại tiếp hình chóp SA₁A₂…A_n.

- Xác định tâm O đường tròn ngoại tiếp đa giác đáy A₁A₂…A_n

- Dựng trục \(\Delta \) của đường tròn ngoại tiếp đa giác đáy A₁A₂…A_n.( \(\Delta \)là đường thẳng đi qua tâm O đường tròn ngoại tiếp đa giác đáy và vuông góc với mặt phẳng đáy.)

- Vẽ mặt phẳng trung trực (P) của một cạnh bên bất kì của hình chóp.

- Giả sử \(I = \Delta  \cap \left( P \right)\)khi đó I là tâm mặt cầu ngoại tiếp cần dựng.

Lưu ý:

a)trong trường hợp sau đây mặt phẳng trung trực có thể thay bằng đường trung trực.

+ Khi hình chóp đều (vì \(\Delta \) đi qua đỉnh S)

+ Khi hình chóp có một cạnh vuông góc với mặt phẳng đáy

b) Có thể phát hiện trục \(\Delta \) dựa vào tính chất của một số hình chóp đặc biệt rồi chứng minh thay vì dựng \(\Delta \) .

c) Khi dựng mặt phẳng trung trực của cạnh bên nên chọn cạnh bên của hình chóp đồng phẳng với trục \(\Delta \) để dễ dàng tính toán bán kính R.

Phương pháp 2: Gọi I là tâm mặt cầu ngoại tiếp hình chóp SA₁A₂…A_n.

- Dựng trục \({\Delta _1}\) của đường tròn ngoại tiếp đa giác đáy A₁A₂…A_n.( \(\Delta \)là đường thẳng đi qua tâm O đường tròn ngoại tiếp đa giác đáy và vuông góc với mặt phẳng đáy.)

- Dựng trục \({\Delta _2}\) của đường tròn ngoại tiếp tam giác của mặt bên sao cho \({\Delta _1}{\Delta _2}\)đồng phẳng

- Giả sử\(I = {\Delta _1} \cap {\Delta _2}\), khi đó I là tâm mặt cầu ngoại tiếp.

Phương pháp 3: Ta chứng minh các đỉnh của hình chóp cùng nhìn hai đỉnh còn lại của hình chóp dưới một góc vuông hoặc tất cả các đỉnh của hình chóp cùng nhìn hai điểm nào đó dưới một góc vuông.

Phương pháp 4: Trong không gian ta dự đoán điểm đặc biệt I nào đó rồi chứng minh I cách đều các đỉnh của hình chóp.

III. Cách xác định tâm và tính bán kính mặt cầu ngoại tiếp của một số hình chóp đặc biệt.

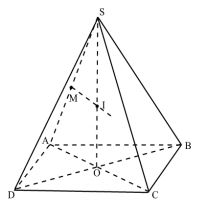
1.Trường hợp hình chóp có các cạnh bên bằng nhau.

Giả sử SA = SB = SC = SD. Ta dựng SO\( \bot \)(ABCD). Trong tam giác SAO kẻ trung trực của SA cắt SO tại I; Ta được I là tâm của mặt cầu ngoại tiếp. Trường hợp này để tính bán kính ta sử dụng tứ giác nội tiếp đường tròn. Cụ thể ABCD nội tiếp đường tròn và có AB cắt CD tại M, khi đó MA.MB = MC.MD.

2. Trường hợp hình chóp có một mặt vuông góc với đáy.

- Xác định trục đường tròn ngoại tiếp đáy

- Xác định trục đường tròn ngoại tiếp của mặt vuông góc đáy

- Giao của hai trục đường tròn là tâm đường tròn ngoại

3. Trường hợp hình chóp có một cạnh vuông góc với đáy.

Giả sử SA vuông góc (ABCD).

 - Xác định trục d đường tròn ngoại tiếp đáy, d song song SA.

- Xác định trung trực cạnh bên SA cắt d tại I thì I là tâm mặt cầu ngoại tiếp.

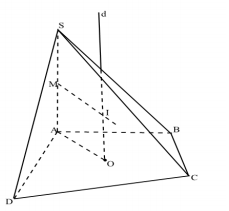
Để tính bán kính ta sử dụng định lý Pitago trong tam giác vuông

IV. Các ví dụ minh họa.

Ví dụ 1: Cho hình chóp S.ABCD có chiều cao SA = a, đáy ABCD là hình thang vuông tại A và B với AB = BC = a, AD = 2a. Gọi E là trung điểm AD. Xác định tâm và tính bán kính mặt cầu ngoại tiếp SCDE theo a.

Phân tích bài toán:

+Nếu nhìn SCDE là hình chóp tam giác S.CDE có mặt đáy CDE là tam giác vuông tại E, ta có ngay trục d đường tròn ngoại tiếp tam giác CDE, khi đó ta tìm trục d’ đường tròn ngoại tiếp tam giác chứa mặt bên nào đó của hình chóp sao cho d và d’ đồng phẳng hoặc tìm hay dựng mặt phẳng trung trực của một cạnh bên nào đó của hình chóp, trong trường hợp này không nên dựng mặt phẳng trung trực của một cạnh bên bất kì, vì các cạnh bên của hình chóp không đồng phẳng với d.

+Nếu nhìn SDCE là hình chóp C.SDE đáy tam giác SCE thì trục đường tròn ngoại tiếp tam giác SCD sẽ song song CE, khi đó ta có thể dựng mặt phẳng trung trực của CE cắt trục tại tâm I

Từ đó ví dụ dụ 1 có thể có các cách giải sau

Cách giải thứ nhất.

Tam giác CDE vuông tại E nên gọi O là trung điểm CD và d là đường thẳng qua O song song SA khi đó d là trục đường tròn ngoại tiếp đáy CDE.

Gọi M, N lần lượt là trung điểm AB và SC.

Ta chứng minh được MN là trục đường tròn ngoại tiếp tam giác SEC

Thật vậy CE\( \bot \) SE nên N là tâm đường tròn ngoại tiếp tam giác SCE.

\(\left\{ {\begin{array}{*{20}{c}}{MN \bot CE}\\{MN \bot SC}\end{array}} \right. \Rightarrow MN \bot \left( {SCE} \right)\)

Dễ dàng chứng minh được MN và d cắt nhau,

gọi\(I = MN \cap d\), khi đó I là tâm mặt cầu ngoại tiếp SCDE

Bán kính\(R = IC = \sqrt {O{I^2} + O{C^2}} \),

trong đó\(OC = \frac{{a\sqrt 2 }}{2};\frac{{OI}}{{O1N}} = \frac{{OM}}{{O1M}} = 3 \Rightarrow OI = \frac{{3a}}{2}\), Suy ra \(R = \frac{{a\sqrt {11} }}{2}\)

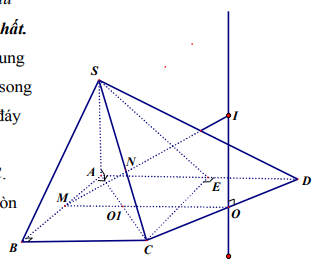
Cách giải thứ hai.

Gọi M, N, P lần lượt là trung điểm của AB, SC và SE, ta có AMNP là hình bình hành và (AMNP) là mặt phẳng trung trực SE, vì

AP\( \bot \) SE ( Tam giác ASE cân tại A)

NP \( \bot \) SE ( NP//AB, AB \( \bot \) SE).

Gọi O là trung điểm CD ta có O là tâm đường tròn ngoại tiếp tam giác CDE. Đường thẳng d đi qua O song song SA là trục đường tròn ngoại tiếp đáy ECD.

\[MN \subset \left( {AMNP} \right)\]cắt d tại I, ta được I là tâm mặt cầu ngoại tiếp SECD.

Bán kính \(R = IC = \sqrt {O{I^2} + O{C^2}} \)

Trong đó \(OC = \frac{{a\sqrt 2 }}{2};\frac{{OI}}{{O1N}} = \frac{{OM}}{{O1M}} = 3 \Rightarrow OI = \frac{{3a}}{2}\)

Suy ra \(R = \frac{{a\sqrt {11} }}{2}\)

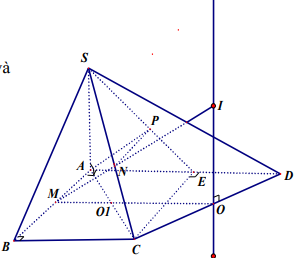
Cách giải thứ ba:

Nếu nhìn tứ diện SECD là hình chóp C.SED ta có đường cao CE và mặt đáy là tam giác SED, có góc SED > 90⁰ .

Gọi O là tâm đường tròn ngoại tiếp tam giác SDE và d là trục đường tròn ngoại tiếp đáy SDE, Khi đó d // CE.

Dựng mặt phẳng trung trực (P) của CE đi qua trung điểm M của CE cắt d tại I

Ta được I là tâm mặt cầu ngoại tiếp CSDE.

Bán kính \(R = IE = \sqrt {E{M^2} + O{E^2}} \)

Với R₁= OE là bán kính đường tròn ngoại tiếp tam giác SED.

Tam giác SED có ED = a, SE =\(a\sqrt 2 \), SD = \(a\sqrt 5 \)

Theo định lí hàm số côsin ta tính được góc SED = 135⁰

Theo định lí hàm sin \({R_1} = \frac{{SD}}{{2\sin E}} = \frac{{a\sqrt {10} }}{2}\)

Suy ra \(R = \frac{{a\sqrt {11} }}{2}\)

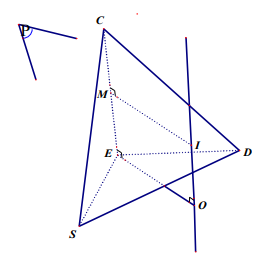
Ví dụ 2: Cho hình S.ABCD, đường cao SA = 2a đáy ABCD là hình thang cân đáy lớn AD = 2a, AB = BC = CD = a. Tính bán kính mặt cầu ngoại tiếp hình chóp S.ABC.

Phân tích bài toán.

+Hình chóp SABC có SA là đường cao nên theo phương pháp giải chúng ta có thể sử dụng đúng phương pháp dựng tâm mặt cầu ngoại tiếp chóp S.ABC . Có trục đường tròn ngoại tiếp đáy song song SA như vậy sẽ chọn mặt phẳng trung trực của cạnh SA, xác định thêm tâm đường tròn ngoại tiếp tam giác ABC là xong.

+ Đáy là hình thang cân với AD = 2a, AB = BC = CD = a nên ta nghĩ đến việc xem xét các quan hệ vuông góc từ số liệu bài toán và định lí 3 đường vuông góc để chứng minh A,B,C cùng nhìn SD dưới một góc vuông.

Từ đó ta có các cách giải sau:

Cách giải thứ nhất

Gọi E, F lần lượt là trung điểm AD và BC có BE là trung trực AC và EF là trung trực BC nên E là tâm đường tròn ngoại tiếp tam giác ABC.

Trong mp(SAD) đường thẳng d qua E song song SA là trục đường tròn ngoại tiếp tam giác ABC.

Gọi (P) là mặt phẳng trung trực SA.

khi đó \(\left( P \right) \cap d = I\) là tâm mặt cầu ngoại tiếp chóp S.ABC

Bán kính \(R = IA = \sqrt {A{E^2} + I{E^2}}  = a\sqrt 2 \)

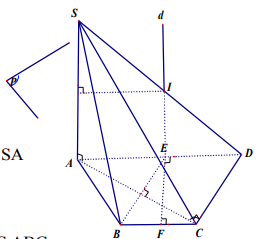
Cách giải thứ hai.

Ta có SA\( \bot \) AD. Gọi E là trung điểm AD khi đó EC = ED = EA = a

 nên AC \( \bot \) CD suy ra SC \( \bot \) CD

Tương tự SB \( \bot \) BD

Do đó A, B, C, S, D nằm trêm mặt cầu đường kính SD.

Bán kính mặt cầu ngoại tiếp S.ABC là \(R = \frac{{SD}}{2} = a\sqrt 2 \)

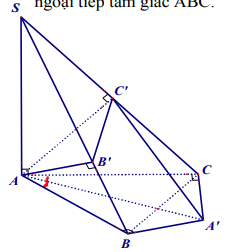
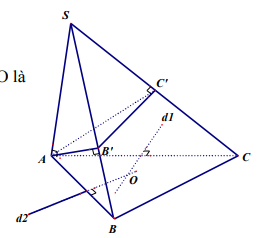
Ví dụ 3: Cho hình chóp S.ABC có SA vuông góc mặt phẳng (ABC). AC = b, AB = c, góc BAC = \(\alpha \) . Gọi B’, C’ lần lượt là hình chiếu vuông góc của A lên SB, SC. Xác định tâm và tính bán kính mặt cầu đó theo b, c và \(\alpha \) .

Cách giải thứ nhất.

Gọi AA’ là đường kính của đường tròn ngoại tiếp tam giác ABC.

Khi đó AC \( \bot \) A’C, AB \( \bot \) A’B.

Ta chứng minh AC’ \( \bot \) A’C’:

SA \( \bot \) A’C ( do SA \( \bot \) (ABC))

AC \( \bot \) A’C

Þ A’C \( \bot \) AC’.

Mà AC’ \( \bot \) SC

ÞAC’ \( \bot \) A’C’

Tương tự AB’ \( \bot \) A’B’ Như vậy B, C, B’, C’ cùng nhìn AA’ dưới một góc vuông nên A, B, C, C’, B’ cùng thuộc mặt cầu đường kính AA’.

Tính bán kính: Gọi R là bán kính mặt cầu đi qua A, B, C, C’, B’ thì R cũng là bán kính đường tròn ngoại tiếp tam giác ABC.

Trong tam giác ABC:

BC²  = AB² + AC²  - 2AB.AC cosA

= \({c^2} + {b^2} - 2bc\cos \alpha  \Rightarrow BC = \sqrt {{b^2} + {c^2} - 2bc\cos \alpha } \)

Trong tam giác ABC:

 \(\frac{{BC}}{{\sin A}} = 2R \Rightarrow R = \frac{{2\sqrt {{b^2} + {c^2} - 2bc\cos \alpha } }}{{\sin \alpha }}\)

Vậy tâm mặt cầu ngoại tiếp A.BCC’B’ là I trung điểm AA’ bán kính

\(R = \frac{{2\sqrt {{b^2} + {c^2} - 2bc\cos \alpha } }}{{\sin \alpha }}\)

Cách giải thứ 2:

Tam giác ABB’ vuông tại B’ nên trong (ABC) dựng đườngtrung trực d2 của AB, tam giác ACC’ vuông tại C’ nên trong mp(ABC) dựng đường trung trực d1 của AC.

Gọi \(O = {d_1} \cap {d_2}\)ta có OA = OB = OB’ = OC = OC’ nên O là tâm mặt cầu ngoại tiếp ABCC’B’ đồng thời là tâm đường tròn ngoại tiếp tam giác ABC

Bán kính R = OA

Trong tam giác ABC:

\(\frac{{BC}}{{\sin A}} = 2R \Rightarrow R = \frac{{2\sqrt {{b^2} + {c^2} - 2bc\cos \alpha } }}{{\sin \alpha }}\)

V. Bài tập tương tự

Bài 1: Cho hình chóp SABCD có đáy là hình vuông cạnh a, SA = SB = a. mặt phẳng (SAB) vuông góc (ABCD). Tính diện tích mặt cầu ngoại tiếp SABCD.

Bài 2: Cho tứ diện ABCD biết AB = BC = AC = BD = a và AD = b, hai mặt phẳng (ACD) và (BCD) vuông góc với nhau. Tính diện tích mặt cầu ngoại tiếp tứ diện ABCD.

Bài 3:Cho chóp SABC có SA vuông góc đáy và SA = a, AB = b, AC = c. Xác định tâm và bán kính mặt cầu ngoại tiếp chóp trong các trường hợp sau:

a) Góc BAC bằng 90⁰ .

b) Góc BAC bằng 60⁰ và b = c.

c) Góc BAC bằng 120⁰ và b = c.

Bài 4: Cho tứ diện ABCD có AD = BC = a, BC = AD = b và AC = BD = c. Tính bán kính mặt cầu ngoại tiếp tứ diện.