Tailieumoi.vn xin giới thiệu Bài tập Toán 9 Chương 1 Bài 9:Căn bậc ba. Bài viết gồm 50 bài tập với đầy đủ các mức độ và có hướng dẫn giải chi tiết sẽ giúp học sinh ôn luyện kiến thức và rèn luyện kĩ năng làm bài tập Toán 9. Ngoài ra, bài viết còn có phần tóm tắt nội dung chính lý thuyết Chương 1 Bài 9: Căn bậc ba. Mời các bạn đón xem:
Bài tập Toán 9 Chương 1 Bài 9: Căn bậc ba
A. Bài tập Căn bậc ba
I. Bài tập trắc nghiệm
Câu 1: Kết quả so sánh nào sau đây sai ?
A. 5 > ∛123 B. 5∛6 = 6∛5
C. 3∛2 < ∛55 D. 3∛4 > 2∛13
Chọn đáp án B.
Câu 2: Kết quả của phép tính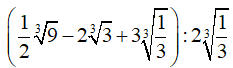 
là ?
Ta có
Chọn đáp án C.
Câu 3: Kết quả rút gọn của biểu thức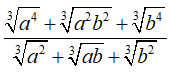 
là ?
Ta có:
Chọn đáp án C.
Câu 4: Cho biểu thức
với x > 0 và x ≠ 8. Rút gọn P ta được ?
A. 2 B. 2 - 2∛x C. ∛x D. 1/2
Ta có:
Chọn đáp án A.
Câu 5: Kết quả của phép tính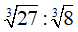 
là = ?
Ta có :
Chọn đáp án B
Câu 6: Tính 
A. 15
B. -1
C.17
D. 1
Ta có:
Chọn đáp án C.
Câu 7: Tìm kết quả đúng 
A. -3
B. 3
C. 6
D.- 6
Ta có:
Chọn đáp án A.
Câu 8: Tìm x biết 
A. x = 1
B. x = 13
C.x = 4
D.x = 6
Ta có :
Chọn đáp án B.
Câu 9: Rút gọn 
A. a
B.2a
C. – 2a
D. – a
Ta có:
Chọn đáp án D.
Câu 10: Rút gọn 
A. -5b2(a+1)
B.5b2(a+1)
C. -5b2(a -1)
D. Đáp án khác
Ta có:
Chọn đáp án A.
Câu 11: Thu gọn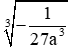 
với a ≠ 0 ta được
Đáp án cần chọn là: C
Câu 12: Rút gọn biểu thức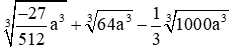 
ta được
Đáp án cần chọn là: A
Câu 13: Rút gọn biểu thức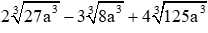 
ta được
A. 14a
B. 20a
C. 9a
D. −8a
Đáp án cần chọn là: B
Câu 14: Rút gọn biểu thức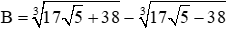 
ta được
Đáp án cần chọn là: A
Câu 15: Rút gọn biểu thức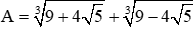 
ta được
Đáp án cần chọn là: A
Câu 1: Chứng minh rằng giá trị của biểu thức sau không phụ thuộc vào giá trị của biến:
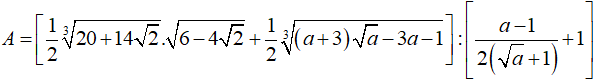
Ta có:
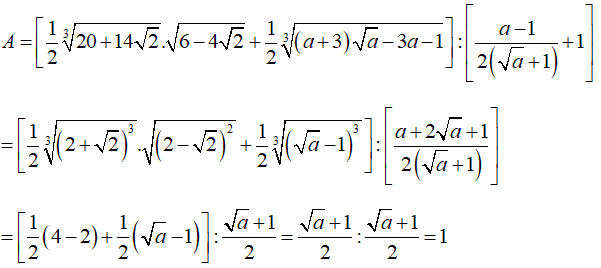
Vậy A không phụ thuộc vào giá trị của biến.
Câu 2: Giải phương trình sau đây:
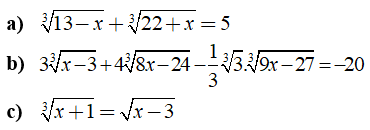
a) Ta có:
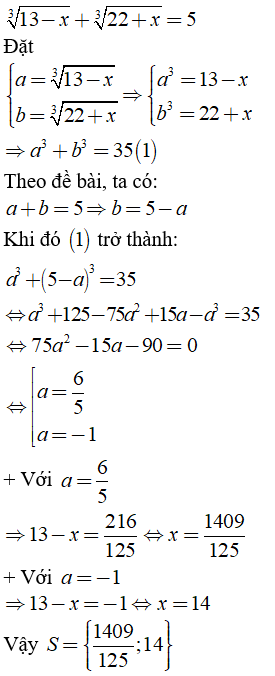
b) Ta có:
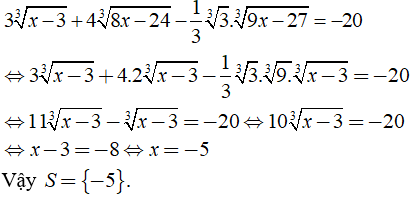
c) Ta có:
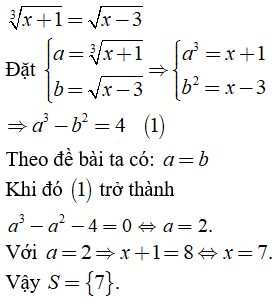
Câu 3: Rút gọn các biểu thức sau
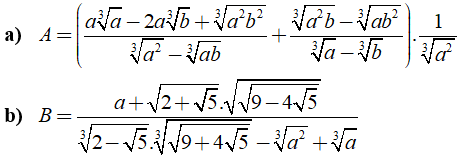
a) Ta có:
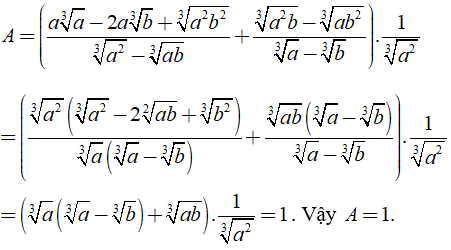
b) Ta có
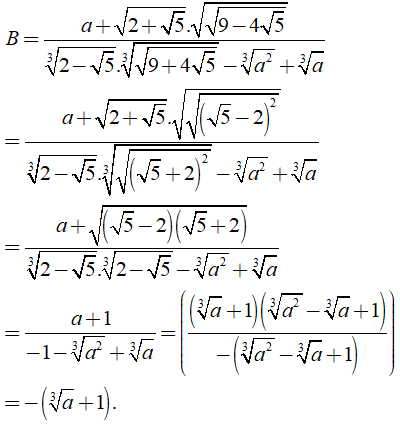
III. Bài tập vận dụng
Câu 1: Chứng minh rằng giá trị của biểu thức sau không phụ thuộc vào giá trị của biến:
Câu 2: Giải phương trình sau đây:
Câu 3: Rút gọn các biểu thức sau
B. Lý thuyết Căn bậc ba
1. Khái niệm căn bậc ba
Định nghĩa: Căn bậc ba của một số thực a là số x sao cho x3 = a.
Ví dụ 1.
3 là căn bậc ba của 27, vì 33 = 27.
– 2 là căn bậc ba của – 8, vì (– 2)3 = – 8.
• Mỗi số a đều có duy nhất một căn bậc ba.
• Căn bậc ba của một số a được kí hiệu là (số 3 gọi là chỉ số căn).
• Phép lấy căn bậc ba của một số gọi là phép khai căn bậc ba.
Chú ý. Từ định nghĩa căn bậc ba, ta có .
Ví dụ 2. vì 73 = 343;
vì (− 4)3 = − 64.
Nhận xét:
- Căn bậc ba của số dương là số dương;
- Căn bậc ba của số âm là số âm;
- Căn bậc ba của số 0 là số 0.
Ví dụ 3.
- Căn bậc ba của 125 là 5 vì 53 = 125;
- Căn bậc ba của −1 là −1 vì (−1)3 = −1;
- Căn bậc ba của số 0 là số 0.
2. Tính chất
• a < b .
• .
• Với b ≠ 0, ta có: .
Ví dụ 4.
+ 5 < 6 Û .
+ .
+ .
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
