Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập bộ bài tập Các dạng Giải bài toán bằng cách lập hệ phương trình, tài liệu bao gồm 4 trang, tuyển chọn bài tập Các dạng Giải bài toán bằng cách lập hệ phương trình đầy đủ lý thuyết, phương pháp giải chi tiết và bài tập, giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kì thi môn Toán sắp tới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây:

GIẢI BÀI TOÁN BẰNG CÁCH LẬP HỆ PHƯƠNG TRÌNH

A. Các kiến thức cần nhớ

Các bước giải bài toán bằng cách lập hệ phương trình

Bước 1. Lập hệ phương trình:

- Chọn các ẩn số và đặt điều kiện thích hợp cho các ẩn số;

- Biểu diễn các đại lượng chưa biết theo các ẩn và các đại lượng đã biết;

-Lập hệ phương trình biểu thị mối quan hệ giữa các đại lượng

Bước 2. Giải hệ phương trình vừa thu được.

Bước 3. Kết luận

- Kiểm tra xem trong các nghiệm của hệ phương trình, nghiệm nào thỏa mãn điều kiện của ẩn.

- Kết luận bài toán.

B. Các dạng toán thường gặp

Dạng 1: Toán liên quan đến mối quan hệ giữa các số

Phương pháp:

Ta thường sử dụng các kiến thức  sau:

+) Biểu diễn số có hai chữ số : $\overline{ab}=10a+b$ trong đó

$a$ là chữ số hàng chục và $0<a\le 9$, $a\in \mathbb{N}$,

$b$ là chữ số hàng đơn vị và $0\le b\le 9,b\in \mathbb{N}$.

+) Biểu diễn số có ba chữ số: $\overline{abc}=100a+10b+c$ trong đó

$a$ là chữ số hàng trăm và $0<a\le 9$, $a\in \mathbb{N}$,

$b$ là chữ số hàng chục và $0\le b\le 9,b\in \mathbb{N}$,

$c$ là chữ số hàng đơn vị và $0\le c\le 9,c\in \mathbb{N}$.

Dạng 2: Toán chuyển động

Phương pháp:

Ta thường sử dụng các công thức $S=v.t$, $v={\displaystyle \frac{S}{t}},t={\displaystyle \frac{S}{v}}$

Với $S:$ là quãng đường, $v:$ là vận tốc, $t$: thời gian

Dạng 3: Toán làm chung công việc

Phương pháp:

Một số lưu ý khi giải bài toán làm chung công việc

- Có ba đại lượng tham gia là: Toàn bộ công việc , phần công việc làm được trong một đơn vị thời gian (năng suất) và thời gian.

- Nếu một đội làm xong công việc trong $x$ ngày thì một ngày đội dó làm được ${\displaystyle \frac{1}{x}}$ công việc.

- Xem toàn bộ công việc là $1$ (công việc).

Dạng 4: Toán phần trăm

Phương pháp:

1. Các bước giải bài toán bằng cách lập phương trình hoặc hệ phương trình

+ Bước 1: Chọn ẩn, đơn vị cho ẩn, điều kiện thích hợp cho ẩn

+ Bước 2: Biểu đạt các đại lượng khác theo ẩn

+ Bước 3: Dựa vào các dữ kiện của bài toán để lập phương trình hoặc hệ phương trình

+ Bước 4: Giải phương trình hoặc hệ phương trình

+ Bước 5: So sánh kết quả bài toán, tìm kết quả thích hợp và kết luận

2. Lưu ý:

+ Nếu tổng số sản phẩm là x, số sản phẩm vượt mức a% thì có x+a%x sản phẩm

+ Nếu tổng số sản phẩm là x, số sản phẩm giảm a% thì có x – a%x sản phẩm

Dạng 5: Toán có nội dung hình học

Phương pháp:

Một số công thức cần nhớ

Với tam giác:

Diện tích = (Đường cao x Cạnh đáy) $:2$

Chu vi = Tổng độ dài ba cạnh

Với tam giác vuông: Diện tích = Tích hai cạnh góc vuông$:2$

Với hình chữ nhật: 

Diện tích = Chiều dài. Chiều rộng

Chu vi=(Chiều dài + chiều rộng) $.2$

Với hình vuông cạnh $a$

Diện tích = $a^2$

Chu vi = Cạnh . $4$

C. Ví dụ minh họa

Các Công thức cần lưu ý khi gbt bc lpt hpt.

(S - quãng đường; V - vận tốc; T- thời gian );

2. Chuyển động của tàu, thuyền khi có sự tác động của dòng nước;

Ví dụ 1: Một mảnh vườn hình chữ nhật có chu vi 34m. Nếu tăng chiều dài thêm 3m và tăng chiều rộng thêm 2m thì diện tích tăng thêm 45m². Hãy tính chiều dài, chiều rộng của mảnh vườn.

Hướng dẫn giải

Gọi chiều rộng và chiều dài của mảnh vườn là x và y (m, x > 0, y > 0).

Theo đề bài ta có:

Chu vi hình chữ nhật là: 2(x + y) = 34. (1)

Hình chữ nhật mới có chiều dài (y + 3)m, chiều rộng (x +2)m nên có diện tích là (x + 2)(y + 3). Do hình chữ nhật mới có diện tích tăng thêm 45m² nên ta có phương trình:

(x+2)(y+3)= xy + 45 (2)

Từ (1) và (2) ta có hệ phương trình:

Ví dụ 2: Tìm số có hai chữ số, biết rằng nếu đổi chỗ hai chữ số của nó thì được một số lớn hơn số đã cho là 72 và tổng của số mới và số đã cho là 110.

Hướng dẫn giải

Vậy số cần tìm là 19.

Ví dụ 3: Hai thị xã A và B cách nhau 90km. Một chiếc ôtô khởi hành từ A và một xe máy khởi hành từ B cùng một lúc ngược chiều nhau. Sau khi gặp nhau ôtô chạy thêm 30 phút nữa thì đến B, còn xe máy chạy thêm 2 giờ nữa mới đến A. Tìm vận tốc của mỗi xe.

Hướng dẫn giải

Gọi vận tốc của ôtô và xe máy lần lượt là x và y (km/h, x > 0, y > 0).

Giả sử hai xe gặp nhau tại C. Do ôtô đi hết quãng đường BC trong 30 phút (= 0,5h) và xe máy đi hết quãng đường CA trong 2 giờ nên ta có:

Quãng đường AC dài 2y (km), quãng đường BC dài 0,5x (km).

Thời gian ôtô đi hết quãng đường AC là 2y/x (km/h).

Thời gian xe máy đi trên quãng đường BC là 0,5x/y (km/h).

Do tổng quãng đường AB dài 90km và thời gian hai xe từ lúc xuất phát tới C bằng nhau nên ta có hệ phương trình

Từ (2) suy ra x = 2y (do x > 0, y > 0), thay vào (1) ta có phương trình

3y = 90 ⇔ y = 30 => x = 60 (thỏa mãn x, y > 0).

Vận tốc của ôtô là 60km/h và vận tốc của xe máy là 30km/h.

Ví dụ 4: Hai vật chuyển động đều trên một đường tròn đường kính 20cm, xuất phát cùng một lúc, từ một điểm, nếu chuyển động cùng chiều cứ 20 giây chúng lại gặp nhau, nếu chuyển động ngược chiều thì cứ 4 giây chúng lại gặp nhau. Tìm vận tốc của mỗi vật.

Hướng dẫn giải:

Gọi vận tốc của hai vật lần lượt là x (cm/s) và y (cm/s). ( x , y > 0, giả sử x > y)

Vì nếu chuyển động cùng chiều cứ 20 giây chúng lại gặp nhau nên hiệu quãng đường đi được trong 20 giây của hai vật là chu vi của đường tròn, do đó: 20x – 20y = 20π

Vì nếu chuyển động ngược chiều thì cứ 4 giây chúng lại gặp nhau nên tổng quãng đường đi được trong 4 giây của hai vật là chu vi của đường tròn, do đó: 4x + 4y = 20 π

Cộng vế theo vế của hai phương trình trên ta được: 2x=6π ⇔ x =3π ( tm)

Với x=3π ⇒ y = 5π-3π = 2π (tm)

Vậy vận tốc của hai vật lần lượt là: 3π(cm/s),2π(cm/s)

Ví dụ 5: Tìm số có hai chữ số biết chữ số ở hàng chục lớn hơn chữ số hàng đơn vị là 2. Số đó gấp 7 lần tổng hai chữ số của nó.

Hướng dẫn giải:

Gọi số cần tìm là $\overline{ab}$ với 

Vì chữ số ở hàng chục lớn hơn chữ số hàng đơn vị là 2, nên ta có: a – b = 2

Vì số đó gấp 7 lần tổng hai chữ số của nó, nên ta có: 10a + b = 7(a + b)

Nhân pt (1) với 3 ta được: 3a – 3b = 6 (3)

Lấy pt (3) – pt (2) ta được: 3b = 6 ⇔ b = 2 ( tm )

Với b = 2 ⇒ a = 4 ( tm)

Vậy số cần tìm là: 42.

Ví dụ 6: Hai người thợ cùng làm chung một công việc trong 16 giờ thi xong. Nếu người thứ nhất làm trong 3 giờ và người thứ hai làm trong 6 giờ thì được 25% khối lượng cộng việc. Hỏi mỗi người làm một mình thì hết bao lâu?

Hướng dẫn giải:

Gọi thời gian để người thứ nhất làm xong công việc đó là x (giờ), ( x > 16)

Gọi thời gian để người thứ hai làm xong công việc đó là y (giờ), ( y > 16)

Vì hai người cùng làm chung công việc trong 16 giờ thi xong, nên ta có: 

Vì người thứ nhất làm trong 3 giờ và người thứ hai làm trong 6 giờ thì được 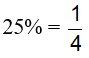 khối lượng cộng việc, nên ta có:

Nhân pt(1) với 3 ta được: 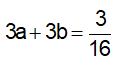 , rồi trừ vế với vế cho pt(2) ta được:

Vậy người thứ nhất làm hết 24 giờ, người thứ hai làm hết 48 giờ.

D. Bài tập vận dụng

Bài toán 1. Dạng toán chuyển động

Một Ô tô đi từ A đến B cùng một lúc, Ô tô thứ hai đi từ B về A với vận tốc bằng  vận tốc Ô tô thứ nhất. Sau 5 giờ chúng gặp nhau. Hỏi mỗi Ô tô đi cả quãng đường AB mất bao lâu.

Đáp án

Gọi thời gian ô tô đi từ A đến B là ;

Ta có vận tốc Ô tô đi từ A đến B là : 

Vận tốc Ô tô đi từ B về A là: 

Sau 5 giờ Ô tô đi từ A đến B đi được quãng đường là; 5 . 

Sau 5 giờ ô tô đi từ B đến A đi được quãng đường là; 

Vì sau 5 giờ chúng gặp nhau do đó ta có phương trình:

Giải phương trình ta được: 

Bài toán 2: Hai ô tô cùng khởi hành một lúc từ hai tỉnh A và B cách nhau 160 km, đi ngược chiều nhau và gặp nhau sau 2 giờ. Tìm vận tốc của mỗi ô tô biết rằng nếu ô tô đi từ A tăng vận tốc thêm 10 km/h sẽ bằng hai lần vận tốc ôtô đi từ B.

Bài toán 3: Một người đi xe đạp từ A đến B với vận tốc 9km/h. Khi đi từ B về A người ấy đi đường khác dài hơn 6 km, với vận tốc 12km/h nên thời gian ít hơn thời gian khi đi là 20 phút. Tính quãng đường AB?

Bài toán 4: Hai ca nô cùng khởi hành từ hai bến A, B cách nhau 85 km , đi ngược chiều nhau và gặp nhau sau 1 giờ 40 phút.Tính vận tốc riêng của mỗi ca nô biết rằng vận tốc của ca nô xuôi dòng lớn hơn vận tốc của ca nô ngược dòng là 9 km/h (có cả vận tốc dòng nước) và vận tốc dòng nước là 3 km/h.

Dạng 2: Toán thêm bớt một lượng

Bài 5. Hai lớp 9A và 9B có tổng cộng 70 học sinh. nếu chuyển 5 học sinh từ lớp 9A sang lớp 9B thì số học sinh ở hai lớp bằng nhau. Tính số học sinh mỗi lớp.

Bài 6: Hai thùng đựng dầu: Thùng thứ nhất có 120 lít, thùng thứ hai có 90 lít. Sau khi lấy ra ở thùng thứ nhát một lượng dầu gấp ba lượng dầu lấy ra ở thùng thứ hai, thì lượng dầu còn lại trong thùng thứ hai gấp đôi lượng dầu còn lại trong thùng thứ nhất. Hỏi đã lấy ra bao nhiêu lít dầu ở mỗi thùng?

Dạng 3: Toán phần trăm

Bài 7. Hai trường A, B có 250 học sinh lớp 9 dự thi vào lớp 10, kết quả có 210 học sinh đã trúng tuyển. Tính riêng tỉ lệ đỗ thì trường A đạt 80%, trường B đạt 90%. Hỏi mỗi trường có bao nhiêu học sinh lớp 9 dự thi vào lớp 10.

Dạng 4: Toán làm chung làm riêng

Bài 8. Hai vòi nước cùng chảy vào một bể không có nước sau 2 giờ 55 phút thì đầy bể. Nếu chảy riêng thì vòi thứ nhất cần ít thời gian hơn vòi thứ hai là 2 giờ. Tính thời gian để mỗi vòi chảy riêng thì đầy bể.

Bài 9. Hai tổ cùng làm chung một công việc hoàn thành sau 15 giờ. Nếu tổ một làm trong 5 giờ, tổ hai làm trong 3 giờ thì được 30% công việc. Hỏi nếu làm riêng thì mỗi tổ hoàn thành trong bao lâu.

E. Bài tập trắc nghiệm

Câu 1: Tìm hai số biết tổng của chúng là 1006, nếu lấy số lớn chia cho số bé thì được thương là 2 và số dư là 124. ( biết hai số đó là số nguyên dương)

A. số lớn: 712 và số bé : 294

B. số lớn: 702 và số bé : 304

C. số lớn: 612 và số bé : 394

D. số lớn: 512 và số bé : 494

Lời giải:

Đáp án: A

Gọi hai số cần tìm lần lượt là x, y ( x > y, 0 < x, y < 1006 )

Vì tổng của hai số là 1006, nên ta có: x + y = 1006

Vì số lớn chia cho số bé thì được thương là 2 và số dư là 124, nên ta có: x = 2y +124

Suy ra hệ phương trình:

Thay x = 2y + 124 vào pt (1) ta được: 2y + 124 + y = 1006 ⇔ 3y = 882 ⇔ y = 294 ( tm )

Với y = 294 ⇒ x = 2.294 + 124 = 712 ( tm )

Vậy hai số cần tìm là: 712 và 294.

Câu 2: Một thửa ruộng hình chữ nhật có chiều rộng ngắn hơn chiều dài 45m. Tính diện tích của thửa ruộng, biết nếu giảm chiều dài 2 lần và tăng chiều rộng lên 3 lần thì chu vi không đổi.

A, 640 m²

B, 600 m²

C, 800 m²

D, 900 m²

Lời giải:

Đáp án: D

Gọi chiều dài của thửa ruộng là x (m), ( x > 45)

Gọi chiều rộng của thửa ruộng là y (m) ( 0 < y < x)

Vì thửa ruộng hình chữ nhật có chiều rộng ngắn hơn chiều dài 45m, nên ta có: x – y = 45

Vì nếu giảm chiều dài 2 lần và tăng chiều rộng lên 3 lần thì chu vi không đổi, ta có:

2(0,5x + 3y) = 2(x + y) ⇔ 0,5x + 3y = x + y

Nhân pt (1) với 2 ta được: 2x – 2y = 90, rồi trừ vế với vế cho pt (2) ta được:

1,5x = 90 ⇔ x = 60 (tm )

Với x = 60 ⇒ y = 60 – 45 = 15 ( tm )

Vậy diện tích của thửa ruộng là: 60 . 15 = 900 m₂.

Câu 3: Một hình chữ nhật có chu vi là 70m, nếu giảm chiều rộng 3m và tăng chiều dài lên 5m thì diện không đổi. Tìm chiều rộng và chiều dài?

A. chiều rộng: 15m và chiều dài : 20m

B. chiều rộng: 10m và chiều dài : 25m

C. chiều rộng: 25m và chiều dài : 10m

D. chiều rộng: 5m và chiều dài : 30m

Lời giải:

Đáp án: A

Gọi chiều rộng của hình chữ nhật là x (m), ( 0 < x < 35)

Gọi chiều dài của hình nhật là y (m), ( x <y < 35)

Vì chu vi của hình chữ nhật la 70m, ta có: 2( x + y) = 70 ⇔ x + y = 35

Vì giảm chiều rộng 3m và tăng chiều dài lên 5m thì diện không đổi, ta có: (x – 3)(y + 5) = xy

Từ pt (1) suy ra: x = 35 – y, thay vào pt (2) ta được:

5(35 – y) – 3y = 15 ⇔ 175 – 5y – 3y = 15 ⇔ 8y = 160 ⇔ y = 20 ( tm )

Với y = 20 ⇒ x = 35 – 20 = 15 ( tm )

Vậy chiều rộng của hình chữ nhật là: 15m và chiều dài là: 20m.

Câu 4: Hai đội cùng làm chung một công việc và dự định xong trong 12 ngày thi xong. Họ cùng làm trong 8 ngày, thì đội I được điều đi làm việc khác, đội II làm tiếp. Do cải tiến kỹ thuật năng suất tăng lên gấp đôi nên đội II làm xong cộng việc còn lại trong 3,5 ngày. Hỏi mỗi đội làm một mình thì hết bao lâu?

A. Đội I: 28 ngày và Đội II: 21 ngày

B. Đội I: 28 ngày và Đội II: 24 ngày

C. Đội I: 21 ngày và Đội II: 28 ngày

D. Đội I: 24 ngày và Đội II: 21 ngày

Lời giải:

Đáp án: A

Gọi thời gian để đội I làm xong công việc đó là x (giờ), ( x > 12)

Gọi thời gian để đội II làm xong công việc đó là y (giờ), ( y > 12)

Vì hai đội cùng làm chung dự định xong trong 12 ngày thi xong, nên ta có:

Đội II phải làm khối lượng công việc còn lại là:

Vì cải tiến kỹ thuật năng suất tăng lên gấp đôi nên đội II làm xong cộng việc còn lại trong 3,5 ngày, nên ta có:

Vậy đội I làm trong 28 ngày, đội II làm trong 21 ngày.

Câu 5: Tìm hai số biết tổng của hai số đó bằng 19, tổng các bình phương của hai số đó bằng 185.( biết hai số đó là số nguyên)

A. 11 và 9 hoặc 9 và 11

B. 11 và 8 hoặc 8 và 11

C. 8 và 12 hoặc 12 và 8

D. 10 và 11 hoặc 11 và 10

Lời giải:

Đáp án: B

Gọi hai số cần tìm lần lượt là x và y (x,y ∈ Z )

Vì tổng của hai số đó bằng 19, nên ta có: x + y = 19

Vì tổng các bình phương của hai số đó bằng 185, nên ta có: x² + y² = 185

Vậy hai số cần tìm là 11 và 8 (hoặc 8 và 11).

Câu 6: Hai vòi nước cùng chảy vào một bể trong 1 giờ 20 phút thì đầy bể. Nếu mở vòi thứ nhất chảy trong 10 phút và mở vòi thứ hai chảy trong 12 phút thì được 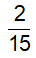 bể. Nếu mỗi vòi chảy một mình thì bao lâu thì chảy đầy bể?

A. vòi thứ nhất : 220 phút và vòi thứ hai: 240 phút.

B. vòi thứ nhất : 120 phút và vòi thứ hai: 140 phút.

C. vòi thứ nhất : 120 phút và vòi thứ hai: 240 phút.

D. vòi thứ nhất : 240 phút và vòi thứ hai: 120 phút.

Lời giải:

Đáp án: c

Đổi 1 giờ 20 phút = 80 phút.

Gọi thời gian để vòi thứ nhất chảy một mình để bể là x (phút), ( x > 80)

Gọi thời gian để vòi thứ hai chảy một mình để bể là y (phút), ( y > 80)

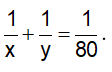
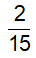
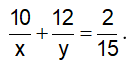
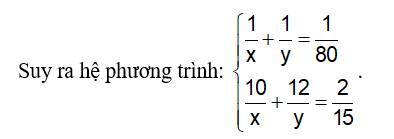
Vì hai vòi nước cùng chảy vào một bể trong 1 giờ 20 phút thì đầy bể, nên ta có:  Vì mở vòi thứ nhất chảy trong 10 phút và mở vòi thứ hai chảy trong 12 phút thì được  bể, ta có: .   

Câu 7: Ở nông trường, có hai máy cày cùng cày trên thửa ruộng hết 2 giờ thì xong, nếu mỗi máy cày riệng thửa ruộng đó thì máy cày thứ 1 cày xong sớm hơn máy cày thứ 2 là 3 giờ. Tính thời gian mỗi máy cày làm việc riêng?

A. máy 1 là: 4 giờ và máy 2 là: 7 giờ.

B. máy 1 là: 3 giờ và máy 2 là: 6 giờ.

C. máy 1 là: 2 giờ và máy 2 là: 5 giờ.

D. máy 1 là: 5 giờ và máy 2 là: 8 giờ.

Lời giải:

Đáp án: B

Gọi thời gian máy cày thứ nhất làm riêng là x (giờ), ( x > 2)

Gọi thời gian máy cày thứ hai làm riêng là y (giờ), ( y > 3)

Trong 1 giờ cả hai máy cày được là :

Vì khi làm riêng thì máy thứ nhất làm xong sớm hơn máy thứ hai là 3 giờ, nên ta có: y = x + 3

Suy ra hệ phương trình:

Thay y = x + 3 vào pt (1) ta được:

Với x = –2 ( loại)

Với x = 3 => y = 6 ( tm )

Vậy máy cày thứ làm hết: 3 giờ, máy cày thứ hai làm hết : 6 giờ.

Câu 8: Một người mua hai mặt hàng A và B. Nếu tăng giá mặt hàng A thêm 10% và tăng thêm giá mặt hàng B thêm 20% thì người đó phải trả 232 nghìn đồng, nếu giảm giá cả hai mặt hàng 10% thì người đó phải trả 180 nghìn đồng. Tính giá tiền mỗi loại.

A. mặt hàng A: 60 nghìn đồng và mặt hàng B: 100 nghìn đồng.

B. mặt hàng A: 70 nghìn đồng và mặt hàng B: 90 nghìn đồng.

C. mặt hàng A: 80 nghìn đồng và mặt hàng B: 120 nghìn đồng.

D. mặt hàng A: 80 nghìn đồng và mặt hàng B: 100 nghìn đồng.

Lời giải:

Đáp án: C

Gọi giá tiền của mặt hàng thứ A là x (nghìn đồng), ( x > 0)

Gọi giá tiền của mặt hàng thứ B là y (nghìn đồng), ( y > 0)

Vì tăng giá mặt hàng A thêm 10% và tăng thêm giá mặt hàng B thêm 20% thì người đó phải trả 232 nghìn đồng, nên ta có: 1,1x + 1,2y = 232.

Vì giảm giá cả hai mặt hàng 10% thì người đó phải trả 180 nghìn đồng,ta có: 0,9x + 0,9y = 180

Thay x = 200 – y vào pt (1) ta được:

1,1(200-y) + 1,2y = 232 ⇔ 220 - 1,1y + 1,2y = 232 ⇔ 0,1y = 12 ⇔ y =120.( tm )

Với y = 120 => x = 80 ( tm )

Vậy giá mặt hàng A: 80 nghìn đồng, giá tiền mặt hàng B: 120 nghìn đồng.

Câu 9: Hai trường A và B của một thị trấn có 210 học sinh thi đỗ vào lớp 10,tỷ lệ trúng tuyển là 84%. Tính riêng thì trường A có 80% học sinh thi đỗ và trường B có 90% học sinh thi đỗ. Hỏi mỗi trường có bao nhiêu học sinh dự thi vào lớp 10.

A. trường A: 150 học sinh và trường B: 100 học sinh.

B. trường A: 110 học sinh và trường B: 140 học sinh.

C. trường A: 120 học sinh và trường B: 130 học sinh.

D. trường A: 100 học sinh và trường B: 150 học sinh.

Lời giải:

Đáp án: A

Gọi số học sinh của trương A tham gia thi vào lớp 10 là x (học sinh), ( 0 < x < 210, x ∈ z⁺ )

Gọi số học sinh của trương B tham gia thi vào lớp 10 là y (học sinh), ( 0 < y < 210, y ∈ z⁺ )

Tổng số học sinh của hai trường tham gia thi vào lớp 10 là: 210 : 84% = 250 ( học sinh)

Ta có: x + y = 250

Vì trường A có 80% học sinh thi đỗ và trường B có 90% học sinh thi đỗ, ta có:

0,8x + 0,9y = 210

Suy ra hệ phương trình:

Thay x = 250 – y vào pt (2) ta được:

0,8(250 – y) + 0,9y = 210 ⇔ 200 – 0,8y + 0,9y = 210 ⇔ 0,1y = 100 ⇔ y = 100 ( tm )

Với y = 100 => x = 250 – 100 = 150 ( tm )

Vậy trường A có 150 học sinh, trường B có 100 học sinh.

Câu 10: Một thửa đất hình chữ nhật có chu vi là 198m và diện tích là 2430 m2. Tính chiều dài và chiều rộng của thửa đất đó?

A. chiều dài : 53m và chiều rộng: 46m

B. chiều dài : 59m và chiều rộng: 40m

C. chiều dài : 57m và chiều rộng: 42m

D. chiều dài : 54m và chiều rộng: 45m

Lời giải:

Đáp án: D

Gọi chiều dài của thửa đất là x (m), ( 0 < x < 99)

Gọi chiều rộng của thửa đát là y(m), ( 0 < y < 99, y < x)

Vì thửa đất có chu vi là 198m , nên ta có: 2(x + y) = 198 ⇔ x + y = 99

Vì thửa đất có diện tích là 2430m2, nên ta có: xy = 2430

Vậy chiều dài của thửa đất : 54m, chiều rộng thửa đất: 45m.

F. Bài tập tự luyện

Câu 1: Một ô tô đi từ A đến B với một vận tốc xác định và trong một thời gian đã định. Nếu vận tốc ô tô giảm 10 km/h thì thời gian tăng 45 phút. Nếu vận tốc ô tô tăng 10 km/h thì thời gian giảm 30 phút. Tính vận tốc và thời gian dự định đi của ô tô.

Câu 2: Hai xí nghiệp theo kế hoạch phải làm tổng cộng 360 dụng cụ. Thực tế, xí nghiệp I vượt mức kế hoạch 10%, xí nghiệp II vượt mức kế hoạch 15%, do đó cả hai xí nghiệp đã làm được 404 dụng cụ. Tính số dụng cụ mỗi xí nghiệp phải làm theo kế hoạch.

Câu 3: Một công nhân dự định làm 72 sản phẩm trong một thời gian đã định. Nhưng thực tế xí nghiệp lại giao 80 sản phẩm. Mặc dù người đó mỗi giờ đã làm thêm một sản phẩm so với dự kiến, nhưng thời gian hoàn thành công việc vẫn chậm so với dự định là 12 phút. Tính số sản phẩm dự kiến làm trong 1 giờ của người đó. Biết mỗi giờ người đó làm không quá 20 sản phẩm.

Câu 4: Một xe khách và một xe du lịch khởi hành đồng thời từ A để đi đến B. Biết vận tốc của xe du lịch lớn hơn vận tốc xe khách là 20 km/h. Do đó nó đến B trước xe khách 50 phút. Tính vận tốc mỗi xe, biết quãng đường AB dài 100 km

Câu 5: Theo kế hoạch, một công nhân phải hoàn thành 60 sản phẩm trong thời gian nhất định. Nhưng do cải tiến kĩ thuật nên mỗi giờ người công nhân đó đã làm thêm được 2 sản phẩm. Vì vậy, chẳng những hoàn thành kế hoạch sớm hơn dự định 30 phút mà còn vượt mức 3 sản phẩm. Hỏi theo kế hoạch, mỗi giờ người đó phải làm bao nhiêu sản phẩm.

Câu 6:  Để hoàn thành một công việc, hai tổ phải làm chung trong 6 giờ. Sau 2 giờ làm chung thì tổ II được điều đi làm việc khác, tổ I đã hoàn thành công việc còn lại trong 10 giờ. Hỏi nếu mỗi tổ làm riêng thì sau bao lâu sẽ xong công việc đó.

Câu 7: Một khu vườn hình chữ nhật có chu vi bằng 48 m. Nếu tăng chiều rộng lên bốn lần và chiều dài lên ba lần thì chu vi của khu vườn sẽ là 162 m. Hãy tìm diện tích của khu vườn ban đầu.

Câu 8: Một người đi xe máy từ A đến B. Vì có việc gấp phải đến B trước thời gian dự định là 45 phút nên người đó tăng vận tốc lên mỗi giờ 10Km. Tính vận tốc mà người đó dự định đi, biết quãng đường AB dài 90 km.

Câu 9: Một đôi công nhân hoàn thành một công việc với mức 420 ngày công thợ (nghĩa là nếu công việc đó chỉ có một người làm thì phải mất 420 ngày). Hãy tính số công nhân của đôi biết rằng nếu đôi tăng thêm 5 người thì số ngày để đôi hoàn thành công việc sẽ giảm đi 7 ngày.

Câu 10 Hai lớp 9A và 9B cùng tham gia lao động vệ sinh sân trường thì công việc hoàn thành sau 1 giờ 20 phút. Nếu mỗi lớp chia nhau làm nửa công việc thì thời gian hoàn tất là 3 giờ. Hỏi nếu mỗi lớp làm một mình thì phải mất bao nhiêu thời gian.

Câu 11: Một tam giác có chiều cao bằng  cạnh đáy. Nếu tăng chiều cao them 3 dm, giảm cạnh đáy đi 2 dm thì diện tích của nó tăng thêm 12 dm. Tính chiều cao và cạnh đáy của tam giác.

Câu 12: Một người đi xe máy từ A đến B. Cùng một lúc một người khác cũng đi xe máy từ B tới A với vận tốc bà̀ng  vận tốc của người thứ nhất. Sau 2 giờ hai người gặp nhau. Hồi mồi người đi cả quãng đường AB hết bao Iâu?

Câu 13: Một thửa ruộng hình chữ nhạt có diện tích 100 m²Tính độ dài các cạnh của thửa ruộng. Biết rằng nếu tăng chiều trọng của thửa ruộng lên 2M và giảm chiều dài của thửa ruộng đi 5m thì diện tích của thửa ruộng tăng thêm m² tăng thêm 2 đơn vị thì tích của chúng bằng 105 đơn vị.

Câu 14: Thời gian ca nô ngược dòng từ A đến B nhỏ hơn thời gian ca nô xuôi dòng từ B trở về A là 2 giờ 40 phút. Tính khoảng cách giữa hai bên A va B. Biết vận tốc dòng nước là 5 km/h, vận tốc riêng của ca nô lúc xóa đông vả lúc ngược dòng bà̀ng nhau.

Câu 15 Người ta dự kiến trồng 300 cây trong một thời gian đã định. Do điều kiện thuận lợi nên mỗi ngày trồng nhiều hơn so với dự kiến là 5 cây. Vì vậy đã trồng xong 300 ấy trước 5 ngày. Hỏi dự kiến ban đầu trồng mỗi ngày là bao nhiêu cây.