Lời giải:

Gọi số sản phẩm của tổ I sản xuất được trong tháng thứ I là x (sản phẩm)

Số sản phẩm của tổ II sản xuất được trong tháng thứ nhất là y (sản phẩm) (x, y ∈ N*)

Tháng thứ nhất 2 tổ sản xuất được 1200 sản phẩm nên ta có phương trình:

 x + y = 1200                  (1)

Tháng thứ hai tổ I vượt mức 30% và tổ II giảm mức đi 22% so với tháng thứ nhất nên 2 tổ đã sản xuất được 1300 sản phẩm, ta có:

Từ (1) và (2) ta có hệ phương trình:

Vậy trong tháng thứ hai tổ II sản xuất được 500.78 : 100 = 390 sản phẩm

Đáp án cần chọn là: C

Lời giải:

Gọi chiều cao của tam giác là h, cạnh đáy tam giác là a. (h, a ∈ N*, a > 3, dm)

Diện tích tam giác ban đầu là 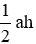 (dm2)

Vì chiều cao bằng 3/4 cạnh đáy nên ta có phương trình: 

Nếu chiều cao tăng thêm 3 dm và cạnh đáy giảm đi 3 dm thì diện tích của nó tăng thêm 12 dm2.

Vậy chiều cao của tam giác bằng 44 dm, cạnh đáy tam giác bằng 33 dm

Suy ra diện tích tam giác ban đầu là 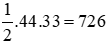 (dm2)

Đáp án cần chọn là: D

Lời giải:

Gọi chiều cao của tam giác là h, cạnh đáy tam giác là a. (h, a , dm); (a > 2)

Diện tích tam giác ban đầu là 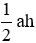 (dm2)

Vì chiều cao bằng 1/4 cạnh đáy nên ta có phương trình 

Nếu chiều cao tăng thêm 2 dm và cạnh đáy giảm đi 2 dm thì diện tích của nó tăng thêm 2,5 dm2.

Vậy chiều cao và cạnh đáy của tấm bìa lần lượt là 1,5 dm và 6 dm

Đáp án cần chọn là: A

Lời giải:

Gọi chiều dài và chiều rộng của khu vương hình chữ nhật lần lượt là x, y

(24 > x > y > 0; m)

Vì khu vườn hình chữ nhật có chu vi bằng 48 m nên ta có (x + y). 2 = 48

Nếu tăng chiều rộng lên bốn lần và chiều dài lên ba lần thì chu vi của khu vườn sẽ là 162m

Nên ta có phương trình (4y + 3x). 2 = 162

Suy ra hệ phương trình 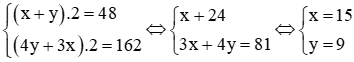 (thỏa mãn)

Vậy diện tích khu vườn ban đầu là 15.9 = 135m2

Đáp án cần chọn là: C

b

Gọi chiều dài và chiều rộng của khu vương hình chữ nhật lần lượt là x, y

(150 > x > y > 0; cm)

Diện tích ban đầu của khu vương là x.y (cm2)

Vì hình chữ nhật có chu vi bằng 300 (cm) nên ta có (x + y). 2 = 300

Nếu tăng chiều rộng thêm 5 cm và giảm chiều dài 5cm thì diện tích tăng 275cm2

Nên ta có phương trình (x − 5).(y + 5) = xy + 275

Vậy chiều rộng của hình chữ nhật ban đầu là 45 cm

Chiều dài của hình chữ nhật ban đầu là 105 cm

Đáp án cần chọn là: B

Lời giải:

Gọi số sách trên hai giá lần lượt là x, y (0 < x, y < 450, cuốn)

Vì hai giá sách có 450 cuốn nên ta có phương trình: x + y = 450 (cuốn)

Nếu chuyển 50 cuốn từ giá thứ nhất sang giá thứ hai thì số sách trên giá thứ hai bằng 4/5 số sách ở giá thứ nhất nên ta có: 

Vậy số sách trên giá thứ nhất là 300 cuốn, số sách trên giá thứ hai là 150 cuốn.

Đáp án cần chọn là: A

Lời giải:

Gọi số viên bi trong hộp thứ nhất và hộp thứ hai lần lượt là x, y (0 < x, y < 360, viên)

Vì Nam có 360 viên bi nên ta có phương trình x + y = 360 (viên bi)

Nếu Nam chuyển 30 viên bi từ hộp thứ hai sang hộp thứ nhất thì số viên bi ở hộp thứ nhất bằng 5/7 số viên bi ở hộp thứ hai nên ta có phương trình  

Vậy số viên bi ở hộp thứ nhất là 120 viên bi, số viên bi ở hộp thứ hai là 240 viên bi.

Đáp án cần chọn là: D

Lời giải:

Gọi năng suất lúa mới và lúa cũ trên 1 ha lần lượt là x; y (x, y > 0) đơn vị: tấn/ha

Vì cấy 60 ha lúa giống mới và 40 ga lúa giống cũ, thu hoạch được tất cả 460 tấn thóc nên ta có 60x + 40y = 460

Vì 3 ha trồng lúa mới thu hoạch được ít hơn 4 ha trồng lúa cũ là 1 tấn nên ta có phương trình: 4y – 3x = 1

Vậy năng suất lúa mới trên 1 ha là 5 tấn

Đáp án cần chọn là: A

Lời giải:

Gọi năng suất lúa mới và lúa cũ trên 1 ha lần lượt là x; y (x, y > 0) đơn vị: tấn/ha

Vì đồng cấy 50 ha lúa giống mới và 30 ha lúa giống cũ, thu hoạch được tất cả 410 tấn thóc nên ta có 50x + 30y = 410

Vì 5 ha trồng lúa mới thu hoạch được nhiều hơn 6 ha trồng lúa cũ là 0,5 tấn nên ta có phương trình: 5x – 6y = 0,5

Vậy năng suất lúa cũ trên 1 ha là 4,5 tấn.

Đáp án cần chọn là: C

Lời giải:

Gọi số học sinh dự thi của hai trường A, B lần lượt là x, y (350 > x, y > 0) (học sinh)

Vì hai trường A, B có tổng cộng 350 học sinh dự thi nên ta có phương trình

x + y = 350 (học sinh)

Vì trường A có 97% và trường B có 96% số học sinh trúng tuyển và cả hai trường đó có 338 học sinh trúng tuyển nên ta có phương trình 97%.x +96%.y = 338

Vậy trường B có 150 học sinh dự thi

Đáp án cần chọn là: B

Lời giải:

Gọi số học sinh của trường thứ nhất dự thi là x (học sinh) (x ∈ N*, x < 300)

Số học sinh của trường thứ hai dự thi là y (học sinh) (y ∈ N*, y < 300)

Hai trường có tất cả 300 học sinh tham gia cuộc thi nên ta có phương trình: x + y = 300  (1)

Trường A có 75% học sinh đạt, trường 2 có 60% đạt nên cả 2 trường có 207 học sinh đạt, ta có: 

Vậy số học sinh của trường thứ nhất dự thi là 180 học sinh; Số học sinh của trường thứ hai dự thi là 120 học sinh.

Đáp án cần chọn là: C

Lời giải:

Gọi chiều dài và chiều rộng của mảnh đất hình chữ nhật lần lượt là: x, y

(21 > x > y > 0; m)

Vì mảnh đất hình chữ nhật có chu vi bằng 42m nên ta có (x + y). 2 = 42

Đường chéo hình chữ nhật dài 15m nên ta có phương trình: x2 + y2 = 152

Vậy chiều rộng mảnh đất ban đầu là 9m

Đáp án cần chọn là: C

Lời giải:

Gọi chiều dài và chiều rộng của mảnh đất hình chữ nhật lần lượt là: x, y

(34 > x > y > 0; m)

Vì mảnh đất hình chữ nhật có nửa chu vi bằng 37m nên ta có x + y = 37

Đường chéo hình chữ nhật dài 26m nên ta có phương trình: x2 + y2 = 262

Vậy chiều dài mảnh đất ban đầu là 24m

Đáp án cần chọn là: A