Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu Đề thi Cuối kì 1 Toán lớp 11 có đáp án, tài liệu bao gồm 4 trang, tuyển chọn đề thi Toán lớp Cuối học kì 1. Đề thi được tổng hợp từ các trường THPT trên cả nước giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho bài thi Giữa học kì 1 môn Toán lớp 11 sắp tới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.
Tài liệu Đề thi Cuối học kì 1 Toán lớp 11 chọn lọc gồm các nội dung sau:
- Ma trận đề kiểm tra giúp học sinh làm quen với cấu trúc đề thi
- Đề thi Cuối kì 1 có đáp án và lời giải chi tiết giúp học sinh ôn tập, rèn luyện
Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây:
MA TRẬN ĐỀ KIỂM TRA HỌC KỲ I
MÔN: TOÁN 11 - Năm học: 2021 – 2022
|
Chủ đề hoặc mạch kiến thức, kĩ năng |
Mức độ nhận thức – Hình thức câu hỏi |
Tổng điểm /10 |
||||
|
1 |
2 |
3 |
4 |
|||
|
TL |
TL |
TL |
TL |
|||
|
I. HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC |
Phương tình lượng giác cơ bản |
Câu 1.1 1,0 |
|
|
|
1 1,0 |
|
Phương trình lượng giác thường gặp… |
|
Câu 1.2 1,0 |
|
Câu 1.3 1,0 |
2 2,0 |
|
|
GTLN và GTNN của hàm số lượng giác |
|
|
Câu 2 1,0 |
|
1 1,0 |
|
|
II. TỔ HỢP- XÁC SUẤT |
Xác suất – Nhị thức Niu-Tơn |
|
Câu 3.1 1,0 |
Câu 3.2 1.0 |
|
2 2,0 |
|
Hoán vị- Chỉnh hợp- Tổ hợp. |
|
|
Câu 3.3 1,0 |
|
1 1,0 |
|
|
IV. PHÉP BIẾN HÌNH TRONG MẶT PHẲNG |
Tìm ảnh của đường tròn qua phép biến hình |
|
Câu 4. 1,0 |
|
|
1 1,0 |
|
III. ĐƯỜNG THẲNG VÀ MẶT PHẢNG TRONG KHÔNG GIAN. QUAN HỆ SONG SONG |
Tìm giao tuyến của hai mặt phẳng- Chứng minh quan hệ song song |
Câu 5.1 1,0 |
|
|
|
1
1,0 |
|
Xác định thiết diện |
|
|
Câu 5.2 1,0 |
|
1
1,0 |
|
|
|
1
2,0 |
3
3,0 |
5 4,0 |
1 1,0 |
10 10,0 |
|
BẢNG MÔ TẢ NỘI DUNG
Câu 1(3đ). Giải các phương trình sau:
1.1(1đ). Giải phương trình lượng giác cơ bản.
1.2(1đ). Giải phương trình lượng giác thường gặp(bậc nhất đối với sin và cos hoặc bậc hai đối với một hàm số lượng giác – Không biến đổi).
1.3(1đ). Giải phương trình lượng giác đưa về dạng tích hoặc có biến đổi phức tạp.
Câu 2(1đ). Tìm GTLN – GTNN hàm số lượng giác.
Câu 3(3đ).
3.1. Tính xác suất( có đếm số các số hoán vị, chỉnh hợp, tổ hợp).
3.2. Tìm hệ số trong khai triển nhị thức Niu-tơn.
3.3. Giải phương trình hoặc bất phương trình có chứa số hoán vị, chỉnh hợp hoặc chứng minh đẳng thức có chứa tổ hợp.
Câu 4.(1đ). Tìm ảnh của điểm hoặc đường thẳng hoặc đường tròn qua phép tịnh tiến hoặc phép vị tự.
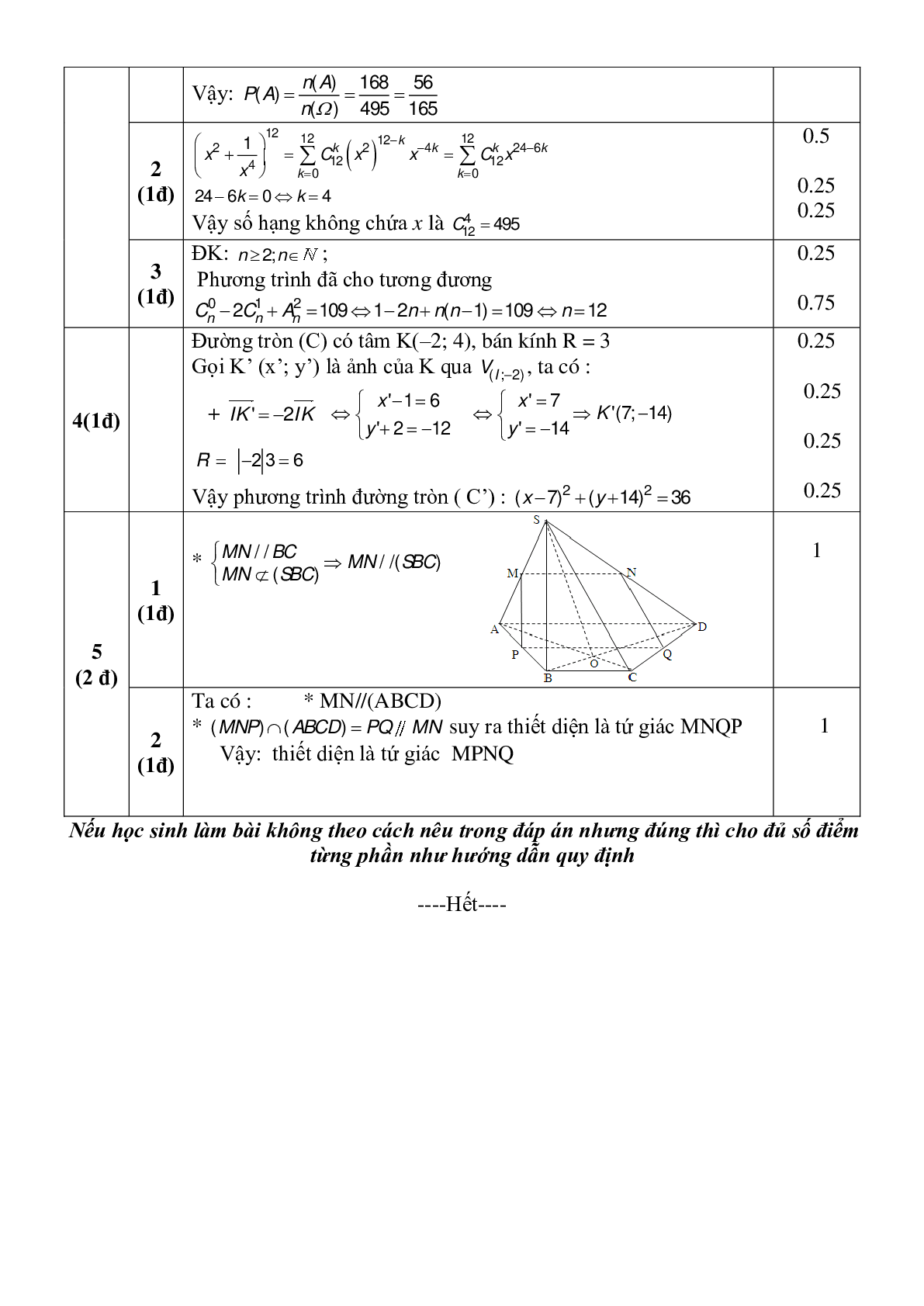
Câu 5.(2đ)
5.1(1đ). Chứng minh quan hệ song song.
5.2.(1đ). Xác định thiết diện.
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
