50 Bài tập Lôgarit (có đáp án)- Toán 12

Trần Thị Hồng Ngày: 08-03-2024 Lớp 12

Tải xuống 9 2.5 K 15

Tailieumoi.vn xin giới thiệu Bài tập Toán 12 Chương 2 Bài 3: Lôgarit. Bài viết gồm 50 bài tập với đầy đủ các mức độ và có hướng dẫn giải chi tiết sẽ giúp học sinh ôn luyện kiến thức và rèn luyện kĩ năng làm bài tập Toán 12. Ngoài ra, bài viết còn có phần tóm tắt nội dung chính lý thuyết Chương 2 Bài 3: Lôgarit. Mời các bạn đón xem:

Bài tập Toán 12 Chương 2 Bài 3: Lôgarit

A. Bài tập Lôgarit

I. Bài tập trắc nghiệm

Bài 1: Tính giá trị của biểu thức

Bài tập trắc nghiệm Giải tích 12 | Câu hỏi trắc nghiệm Giải tích 12

A. -2

B. 2

C. -3log_a5

D. 3log_a5

Lời giải:

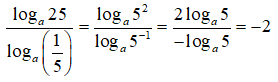
Bài tập trắc nghiệm Giải tích 12 | Câu hỏi trắc nghiệm Giải tích 12

Bài 2: 10log7 bằng:

A. 1

B. log₇10

C. 7

D. log7

Lời giải:

Sử dụng công thức alog_ab

⇒ 10log7 = 7

Bài 3: Cho P = log₃(a²b³) (a,b là các số dương). Khẳng định nào sau đây là đúng ?

A. P = 6log₃a.log₃b

B. P = 2log₃a + 3log₃b

C. P = _{( $\frac{1}{2}$ )}log₃a + ( $\frac{1}{3}$ )log₃b

D. P = (log₃a)².(log₃b)³

Lời giải:

P = log₃a² + log₃b³ = 2log₃a + 3log₃b

Bài 4: Đặt a = log₂7, b = log₂3. Tính log₂( $\frac{56}{9}$ ) theo a và b

A. P = 3 + a - 2b

B. P = 3 + a - b²

C. P = $\frac{3 a}{2 b}$

D. $\frac{3 a}{b^{2}}$

Lời giải:

P = log₂56 - log₂9

= log₂(8.7) - log₂32

= log₂23 + log₂7 - 2log₂3

= 3 + log₂7 - 2log₂3

= 3 + a - 2b

Bài 5: Biết y = 2³x. Hãy biểu thị x theo y

Bài tập trắc nghiệm Giải tích 12 | Câu hỏi trắc nghiệm Giải tích 12

Lời giải:

y = 2³x ⇔ 3x = log₂y ⇔ x = ( $\frac{1}{3}$ )log₂y

Bài 6: Biết 3 + 2log₂x = log₂y . Hãy biểu thị y theo x

A. y = 2x+3

B. y = 8x²

C. y = x²+8

D. y = 3x²

Lời giải:

3 + 2log₂x = log₂y ⇔ log₂23 + log₂x2 = log₂y

Bài 7: Nếu x = (log₈2)log₂8 thì log₃x bằng:

A. -3

B. - $\frac{1}{3}$

C. $\frac{1}{3}$

D. 3

Lời giải:

x = (log₈2)log₂8 = (log₂32)log₂23 = ( $\frac{1}{3}$ )³ = 3-3 => log₃x = -3

Bài 8: Độ pH của một chất được xác định bởi công thức pH = -log[H+] trong đó [H+] là nồng độ ion hyđrô trong chất đó tính theo mol/lít (mol/L). Xác định nồng độ ion H+ của một chất biết rằng độ pH của nó là 2,44

A. 1,1.108 mol/L

C. 3,6.10-3 mol/L

B. 3,2.10-4 mol/L

D. 3,7.10-3 mol/L

Lời giải:

pH = -log[H+]

=> [H+] = 10-pH = 10-2,44 ≈ 0,00363 ≈ 3,6.10-3 (mol/L).

Chọn đáp án C

Bài 9: Rút gọn biểu thức

Bài tập trắc nghiệm Giải tích 12 | Câu hỏi trắc nghiệm Giải tích 12

Lời giải:

Ta có

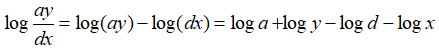
P = loga - logb + logb - logc + logc - logd - (loga + logy - logd - logx)

= -logy + logx = log( $\frac{x}{y}$ )

Chọn đáp án B.

Bài 10: Tính giá trị biểu thức

Bài tập trắc nghiệm Giải tích 12 | Câu hỏi trắc nghiệm Giải tích 12

A. 0,01

B. 0,1

C. 1

D. 10

Lời giải:

Biểu thức đã cho bằng

log100!2 + log100!3 + log100!4 + ... + log100!100 = log100!(2.3.4....10) = log100!100! = 1

Chọn đáp án C

II. Bài tập tự luận có lời giải

Bài 1: Đặt a = log₂3, b = log₃5. Hãy tính biểu thức P = log₆60 theo a và b

Lời giải:

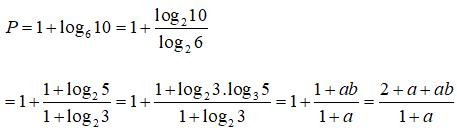
Bài 2:

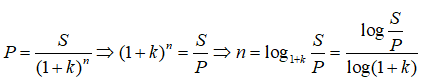
Bài tập trắc nghiệm Giải tích 12 | Câu hỏi trắc nghiệm Giải tích 12

Lời giải:

Bài 3: Tính giá trị của biểu thức log₃100 - log₃18 - log₃50

Lời giải:

log₃100 - log₃18 - log₃50

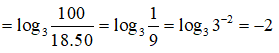
Bài 4: Tính giá trị của biểu thức (log₂3)(log₉4)

Lời giải:

(log₂3)(log₉4) = (log₂3) = (log₃222) = (log₂3)(log₃2) = 1

Bài 5: Khối lượng m của một chất phóng xạ thay đổi theo thời gian t tuân theo công thức

Bài tập trắc nghiệm Giải tích 12 | Câu hỏi trắc nghiệm Giải tích 12

trong đó m₀ là khối lượng chất phóng xạ ban đầu, T là chu kì bán rã. Nếu viết phương trình này dưới dạng m = m₀e-kt thì :

Lời giải:

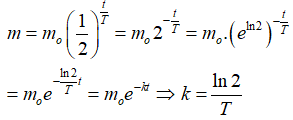
Bài 6: Đặt log₈3 = p và log_nx = 3log_mx . Hãy biểu thị log5 theo p và q

Lời giải:

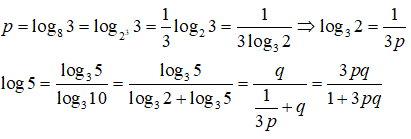
Bài 7: Cho m, n > 1 và log_nx = 3log_mx với mọi x > 0. Hãy biểu thị m theo n

Lời giải:

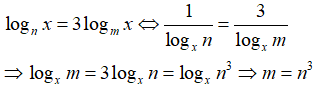
Bài 8: Biết rằng 4a = 5, 5b = 6, 6c = 7, 7d = 8. Tính abcd

Lời giải:

Từ giả thiết ta có: a = log₄5, b = log₅6, c = log₆7, d = log₇8

=> abcd = log₄5.log₅6.log₆7.log₇8 = log₄6log₆7log₇8 = log₄7.log₇8 = log₄8 = log₂223 = ( $\frac{3}{2}$ )log₂2 = $\frac{3}{2}$

Bài 9: Cho b > 1, sinx > 0, cosx > 0 và log_bsinx = a. Khi đó log_bcosx bằng

Lời giải:

Bài tập trắc nghiệm Giải tích 12 | Câu hỏi trắc nghiệm Giải tích 12

Bài 10: Biết rằng log₃y = ( $\frac{1}{2}$ )log₃u + log₃v + 1. Hãy biểu thị y theo u và v

Lời giải:

log₃y = ( $\frac{1}{2}$ )log₃u + log₃v + 1 <=> log₃y = log₃u $\frac{1}{2}$ + log₃v + log₃3 = log₃( $\sqrt{u}$ .v.3) => y = 3 $\sqrt{u}$ .v

III. Bài tập vận dụng

Bài 1 Tìm số k sao cho 2^x = e^kx với mọi số thực x

Bài 2 Độ pH của một chất được xác định bởi công thức pH = -log[H⁺] trong đó H⁺ là nồng độ ion hyđrô trong chất đó tính theo mol/lít (mol/L). Xác định nồng độ ion H⁺ của một chất biết rằng độ pH của nó là 8,06

Bài 3 log₁₂5 bằng?

Bài 4 Cho a, b, c là các số dương. Tính giá trị của biểu thức log_ab².log_bc².log_ca²

Bài 5 Nếu a = log8225 và b = log215 thì giữa a và b có hệ thức

Bài 6 Biết 3 + 2log₂x = log₂y . Hãy biểu thị y theo x

Bài 7 Tính giá trị biểu thức

Bài tập trắc nghiệm Giải tích 12 | Câu hỏi trắc nghiệm Giải tích 12

Bài 8 Đặt a = log₂3, b = log₃5. Hãy tính biểu thức P = log₆60 theo a và b

Bài 9 Tính giá trị của biểu thức log₃100 - log₃18 - log₃50

Bài 10 Tính giá trị của biểu thức (log₂3)(log₉4)

B. Lý thuyết Lôgarit

I. Khái niệm về lôgarit

1. Định nghĩa

Cho hai số dương a; b với a ≠ 1. Số α thỏa mãn đẳng thức a^α = b được gọi là logarit cơ số a của b và kí hiệu là log_ab.

$α = \log_{a} b \Leftrightarrow a^{α} = b$

Ví dụ 1.

a) log₃ 27 = 3 vì 3³ = 27.

b) $\log_{4} (\frac{1}{16}) = - 2$ vì $4^{- 2} = \frac{1}{16}$ .

– Chú ý: Không có logarit của số âm và số 0.

2. Tính chất

Cho hai số dương a và b; a ≠ 1. Ta có các tính chất sau đây:

log_a1 = 0; log_aa = 1

$a^{\log_{a} b} = b; \log_{a} (a^{α}) = α$

Ví dụ 2.

$4^{- 2 \log_{4} 3} = {(4^{\log_{4} 3})}^{- 2}$ $= 3^{- 2} = \frac{1}{9}$

$\log_{3} (\frac{1}{27})$ $= \log_{3} (3^{- 3}) = - 3$

II. Quy tắc tính logarit

1. Logarit của một tích

– Định lí 1. Cho ba số dương a; b₁ ;b₂ với a ≠ 1. Ta có:

$\log_{a} (b_{1} . b {}_{2}) = \log_{a} b_{1} + \log_{a} b {}_{2}$

Logarit của một tích bằng tổng các logarit.

Ví dụ 3.

$\log_{2} 12 + \log_{2} \frac{1}{3} = \log_{2} (12. \frac{1}{3}) = \log_{2} 4 = 2$

– Chú ý:

Định lí 1 có thể mở rộng cho tích n số dương:

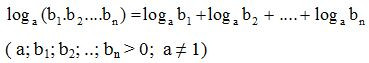
Lý thuyết Lôgarit chi tiết – Toán lớp 12 (ảnh 1)

2. Logarit của một thương

– Định lí 2. Cho ba số dương a; b₁ ;b₂ với a ≠ 1. Ta có:

$\log_{a} \frac{b_{1}}{b_{2}} = \log_{a} b_{1} - \log_{a} b {}_{2}$

Logarit của một thương bằng hiệu các logarit.

Đặc biệt: $\log_{a} \frac{1}{b} = - \log_{a} b$ ( a > 0; b > 0; a ≠ 1)

– Ví dụ 4.

$\log {}_{5} 75 - \log_{5} 3 = \log_{5} \frac{75}{3} = \log_{5} 25 = 2$

3. Logarit của một lũy thừa.

– Định lí 3. Cho hai số dương a; b và a ≠ 1 . Với mọi số α, ta có:

$\log_{a} b^{α} = α \log_{a} b$

Logarit của một lũy thừa bằng tích của số mũ với logarit của cơ số.

– Đặc biệt: $\log_{a} \sqrt[n]{b} = \frac{1}{n} \log_{a} b$

– Ví dụ 5.

$\begin{array}{l} \log_{7} 3^{6} = 6 \log_{7} 3 \\ \log_{3} \sqrt[5]{4} = \frac{1}{5} \log_{3} 4 \end{array}$

III. Đổi cơ số.

– Định lí 4. Cho ba số dương a; b; c với a ≠ 1; c ≠ 1, ta có:

$\log_{a} b = \frac{\log_{c} b}{\log_{c} a}$

– Đặc biệt:

$\begin{array}{l} \log_{a} b = \frac{1}{\log_{b} a} ( b \neq 1) \\ \log_{a^{α}} b = \frac{1}{α} \log_{a} b (α \neq 0) \end{array}$

Ví dụ 6. Tính giá trị các biểu thức sau:

a) $5^{\log_{\frac{1}{125}} 8}$

b) $\log_{2} 3. \log_{3} 4. .... \log_{7} 8$

Lời giải:

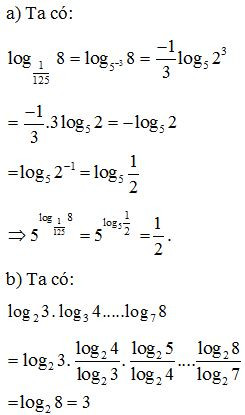
Lý thuyết Lôgarit chi tiết – Toán lớp 12 (ảnh 1)

IV. Logarit thập phân. Logarit tự nhiên.

1. Logarit thập phân

Logarit thập phân là logarit cơ số 10.

log₁₀b thường được viết là logb hoặc lgb.

2. Logarit tự nhiên

– Logarit tự nhiên là logarit cơ số e.

log_eb được viết là lnb.

Tài liệu có 9 trang. Để xem toàn bộ tài liệu, vui lòng tải xuống

Từ khóa :

Đánh giá

0 đánh giá

Đánh giá

Tìm kiếm

Tài Liệu Xem Nhiều

pdf Góc giữa cạnh bên và mặt đáy
3 41.5 K 81
pdf Các công thức mặt nón, mặt cầu, mặt trụ
2 40.1 K 85
pdf Dạng bài tập Khảo sát và vẽ đồ thị hàm hữu tỉ bậc hai trên bậc nhất
10 37.3 K 206
pdf 50 Bài tập Nguyên hàm (có đáp án)- Toán 12
22 31.2 K 460
pdf Vị trí tương đối của đường thẳng và mặt phẳng
9 30.3 K 37