Tailieumoi.vn xin giới thiệu Bài tập Toán 8 Chương 2 Bài 2: Diện tích hình chữ nhật. Bài viết gồm 50 bài tập với đầy đủ các mức độ và có hướng dẫn giải chi tiết sẽ giúp học sinh ôn luyện kiến thức và rèn luyện kĩ năng làm bài tập Toán 8. Ngoài ra, bài viết còn có phần tóm tắt nội dung chính lý thuyết Chương 2 Bài 2:Diện tích hình chữ nhật. Mời các bạn đón xem:

Bài tập Toán 8 Chương 2 Bài 2: Diện tích hình chữ nhật 

A. Bài tập Diện tích hình chữ nhật

I. Bài tập trắc nghiệm

Bài 1: Diện tích hình chữ nhật thay đổi như thế nào nếu chiều rộng tăng 4 lần, chiều dài giảm 2 lần ?

A. Diện tích không đổi.

B. Diện tích giảm 2 lần.

C. Diện tích tăng 2 lần.

D. Cả đáp án A, B, C đều sai.

Lời giải:

Công thức diện tích hình chữ nhật là S_hcn = a.b

Trong đó : a là chiều dài, b là chiều rộng

Theo giả thiết: S_{ban đầu} = a.b

Khi đó ta có: S_sau = 4b.$\frac{1}{2}$a = 2a.b = 2S_{ban đầu}

Do đó, diện tích sau tăng lên 2 lần.

Chọn đáp án C.

Bài 2: Cho hình chữ nhật có chiều dài là 4 cm, chiều rộng là 1,5 cm. Diện tích của hình chữ nhật đó là ?

A. 5 (cm)   

B. 6 (cm²)

C. 6 (cm)   

D. 5 (cm²)

Lời giải:

Công thức diện tích hình chữ nhật là S_hcn = a.b

Trong đó : a là chiều dài, b là chiều rộng

Khi đó ta có: S_hcn = 4. 1,5 = 6( cm² ).

Chọn đáp án B.

Bài 3: Cho hình vuông có độ dài cạnh hình vuông là 4 cm. Diện tích của hình vuông đó là?

A. 8( cm ).   

B. 16( cm )

C. 8( cm² )   

D. 16( cm² )

Lời giải:

Diện tích hình vuông bằng bình phương cạnh của nó: S = a².

Khi đó ta có S_hv = 4.4 = 16 ( cm² ).

Chọn đáp án D.

Bài 4: Cho tam giác vuông, có độ dài hai cạnh góc vuông lần lượt là 6cm, 4cm. Diện tích của tam giác vuông đó là ?

A. 24 (cm²)   

B. 14 (cm²)

C. 12 (cm²)   

D. 10 (cm²)

Lời giải:

Diện tích tam giác vuông bằng nửa tích hai cạnh: S = $\frac{1}{2}$a.b.

Khi đó ta có S = $\frac{1}{2}$. 6. 4 = 12( cm² ).

Chọn đáp án C.

Bài 5: Cho hình vuông có đường chéo là 6( dm ) thì diện tích là ?

A. 12 (cm²)   

B. 18(cm²)

C. 20 (cm²)   

D. 24 (cm²)

Lời giải:

Diện tích hình vuông bằng bình phương cạnh của nó: S = a².

Ngoài công thức này, diện tích hình vuông còn một công thức mở rông là:

Diện tích hình vuôngbằng nửa tích của hai đường chéo

Khi đó ta có : S = $\frac{1}{2}$. 6. 6 = 18( cm² ).

Chọn đáp án B.

Bài 6: Cho một tam giác vuông có độ dài hai cạnh góc vuông là 8cm và 9cm. Một hình vuông khác có diện tích bằng diện tích tam giác. Tính độ dài cạnh hình vuông.

A. 6cm    

B. 7cm

C. 4cm    

D. 8cm

Lời giải:

Diện tích tam giác vuông là: S = ($\frac{1}{2}$).8.9 = 36cm²

Gọi độ dài cạnh hình vuông là a (cm).

Diện tích hình vuông là: S = a² (cm²)

Vì diện tích hình vuông bằng diện tích tam giác nên: a² = 36 nên a = 6cm

Chọn đáp án A

Bài 7: Một hình chữ nhật có chiều rộng là 10cm và diện tích là 120cm². Tính đường chéo của hình chữ nhật?

Lời giải:

Diện tích hình chữ nhật là: S = a.b trong đó a và b lần lượt là chiều dài và chiều rộng của hình chữ nhật

Suy ra: 120 = a.10 nên a = 12

Đường chéo của hình chữ nhật là:

Chọn đáp án C

Bài 8: Một tam giác vuông có diện tích 36cm² và độ dài 1 cạnh góc vuông là 6cm. Tính cạnh huyền?

Lời giải:

Diện tích tam giác vuông là:

trong đó a,b là độ dài 2 cạnh góc vuông

Suy ra:

Cạnh huyền của tam giác vuông là:

Chọn đáp án B

Bài 9: Một hình chữ nhật có độ dài hai cạnh là 3cm và 12cm. Một hình vuông có diện tích bằng diện tích hình chữ nhật. Tính độ dài cạnh hình vuông?

A. 5cm    

B. 6cm

C. 4cm    

D. 7cm

Lời giải:

Diện tích hình chữ nhật là: 3.12 = 36 cm²

Diện tích hình vuông độ dài cạnh bằng a là: S = a² (cm²)

Theo giả thiết ta có: a² = 36 nên a = 6cm

Chọn đáp án B

Bài 10: Khi tăng độ dài cạnh lên 2 lần thì diện tích hình vuông tăng lên bao nhiêu lần?

A. 2    

B. 4

C. 6    

D. 8

Lời giải:

Gọi độ dài cạnh hình vuông ban đầu là a

Diện tích ban đầu của hình vuông là a²

Độ dài cạnh hình vuông khi tăng lên 2 lần là 2a

Diện tích của hình vuông mới là (2a)² = 4a²

Suy ra: diện tích hình vuông tăng lên 4 lần

Chọn đáp án B

II. Bài tập tự luận có lời giải

Bài 1: Cho tam giác ABC, lấy M thuộc BC sao cho BM = 4CM. Hãy chọn câu đúng

Lời giải

Kẻ AH ⊥ BC tại H.

Đáp án cần chọn là: C

Bài 2: Cho tam giác ABC, AM là đường trung tuyến. Biết diện tích của ΔABC bằng 60 cm². Diện tích của tam giác AMC là:

A. S_AMC = 30 cm²

B. S_ABC = 120 cm²     

C. S_AMC = 15 cm²       

D. S_AMC = 40 cm²

Lời giải

Mà AM là đường trung tuyến nên M là trung điểm của BC ⇒ BC = 2AM

Đáp án cần chọn là: A

Bài 3 Cho tam giác ABC, AM là đường trung tuyến. Biết diện tích của ΔABC bằng 40 cm². Diện tích của tam giác AMC là:

A. S_AMC = 80 cm²                              

B. S_ABC = 120 cm²     

C. S_AMC = 20 cm²                               

D. S_AMC = 40 cm²

Lời giải

Mà AM là đường trung tuyến nên M là trung điểm của BC ⇒ BC = 2AM

Đáp án cần chọn là: C

Bài 4 Cho tam giác ABC vuông tại A, biết BC = 5 cm; AC = 3 cm. Diện tích tam giác ABC là:

A. 15 cm²       

B. 5 cm²         

C. 6 cm²         

D. 7, 5 cm²

Lời giải

+ Áp dụng định lý Pytago cho tam giác vuông ABC ta có: BC² = AC² + AB² ⇒ AB² = 5² – 3² ⇒ AB² = 16 ⇒ AB = 4 cm

+ Suy ra 

Đáp án cần chọn là: C

Bài 5 Cho tam giác ABC vuông tại A, biết BC = 13 cm; AC = 5 cm. Diện tích tam giác ABC là:

A. 30 cm²       

B. 60 cm²       

C. 40 cm²       

D. 20 cm²

Lời giải

+ Áp dụng định lý Pytago cho tam giác vuông ABC ta có: BC² = AC² + AB² ⇒ AB² = 13² – 5² ⇒ AB² = 144 ⇒ AB = 12 cm

+ Suy ra 

Đáp án cần chọn là: A

III. Bài tập vận dụng

Bài 1 Một gian phòng có nền hình chữ nhật với kích thước là 4,2m và 5,4m, có một cửa sổ hình chữ nhật kích thước là 1m và 1,6m và một cửa ra vào hình chữ nhật kích thước 1,2m và 2m. Ta coi một gian phòng đạt mức chuẩn về ánh sáng nếu diện tích các cửa bằng 20% diện tích nền nhà. Hỏi gian phòng trên có đạt mức chuẩn về ánh sang hay không?

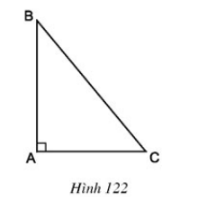
Bài 2 Đo cạnh (đơn vị mm) rồi tính diện tích tam giác vuông dưới đây (h.122)

Bài 3 Xét các hình A, B, C, D, E vẽ trên lưới kẻ ô vuông (h.121), mỗi ô vuông là một đơn vị diện tích.

a) Kiểm tra xem có phải diện tích hình A là diện tích 9 ô vuông, diện tích hình B cũng là diện tích 9 ô vuông hay không ?

b) Vì sao ta nói: Diện tích hình D gấp bốn lần diện tích hình C ?

c) So sánh diện tích hình C với diện tích hình E.

Bài 4 Từ công thức tính diện tích hình chữ nhật hãy suy ra công thức tính diện tích hình vuông, tam giác vuông.

Bài 5 Ba tính chất của diện tích đa giác đã được vận dụng như thế nào khi chứng minh công thức tính diện tích tam giác vuông ?

Bài 6 Diện tích hình chữ nhật thay đổi như thế nào nếu:

a) Chiều dài tăng 2 lần, chiều rộng không đổi?

b) Chiều dài và chiều rộng tăng 3 lần?

c) Chiều dài tăng 4 lần, chiều rộng giảm 4 lần?

Bài 7 Một gian phòng có nền hình chữ nhật với kích thước là 4,2m và 5,4m, có một cửa sổ hình chữ nhật kích thước là 1m và 1,6m và một cửa ra vào hình chữ nhật kích thước 1,2m và 2m.

Bài 8 Ta coi một gian phòng đạt mức chuẩn về ánh sáng nếu diện tích các cửa bằng 20% diện tích nền nhà. Hỏi gian phòng trên có đạt mức chuẩn về ánh sang hay không?

Bài 9 Đo cạnh (đơn vị mm) rồi tính diện tích tam giác vuông dưới đây (h.122)

Bài 10 ABCD là một hình vuông cạnh 12cm, AE = xcm (h123). Tính x sao cho diện tích tam giác ABE bằng $\frac{1}{3}$ diện tích hình vuông ABCD.

Bài 11 Cho một tam giác vuông. Hãy so sánh tổng diện tích của hai hình vuông dựng trên hai cạnh góc vuông với diện tích hình vuông dựng trên cạnh huyền.

Gợi ý: Sử dụng định lí Pitago.

B. Lý thuyết Diện tích hình chữ nhật

1. Khái niệm diện tích đa giác

Số đo của một phần mặt phẳng giới hạn bởi một đa giác được gọi là diện tích đa giác đó.

Mỗi đa giác có một diện tích xác định. Diện tích đa giác là một số dương.

Diện tích đa giác có các tính chất sau

+ Hai tam giác bằng nhau thì có diện tích bằng nhau.

+ Nếu một đa giác được chia thành những đa giác không có điểm trong chung thì diện tích của nó bằng tổng diện tích của những đa giác đó.

2. Công thức diện tích hình chữ nhật

Diện tích hình chữ nhật là tích hai kích thức của nó

Ta có S_hcn = a.b.

Ví dụ: Cho hình chữ nhật có chiều dài bằng 15 cm, chiều rộng bằng 10 cm. Tính diện tích hình chữ nhật đó?

Hướng dẫn:

Diện tích hình chữ nhật cần tìm là S_hcn = 15.10 = 150 ( cm² ).

3. Công thức diện tích hình vuông, diện tích tam giác vuông

Diện tích hình vuông bằng bình phương cạnh của nó: S = a².

Diện tích tam giác vuông bằng nửa tích hai cạnh: S = 1/2a.b.

Ví dụ: Cho hình vuông có độ dài các cạnh bằng 4 cm. Tính diện tích hình vuông ?

Hướng dẫn:

Diện tích hình vuông cần tìm là S_hv = 4² = 16 ( cm² )