Tailieumoi.vn xin giới thiệu Bài tập Toán 8 Chương 2 Bài 4: Diện tích hình thang. Bài viết gồm 50 bài tập với đầy đủ các mức độ và có hướng dẫn giải chi tiết sẽ giúp học sinh ôn luyện kiến thức và rèn luyện kĩ năng làm bài tập Toán 8. Ngoài ra, bài viết còn có phần tóm tắt nội dung chính lý thuyết Chương 2 Bài 4: Diện tích hình thang. Mời các bạn đón xem:

Bài tập Toán 8 Chương 2 Bài 4: Diện tích hình thang

A. Bài tập Diện tích hình thang.

I. Bài tập trắc nghiệm

Bài 1: Hình thang có độ dài đáy lần lượt là $2\sqrt{2}$ cm, 3cm và chiều cao là $3\sqrt{2}$ cm. Diện tích của hình thang là ?

A. 2 (2 + $\sqrt{2}$)cm².

B. 3 ( 2 + $\frac{3}{2\sqrt{2}}$)cm².

C. 3 (3 + $\sqrt{2}$)cm².

D. 3 (2 + $\frac{\sqrt{2}}{2}$)cm²

Lời giải:

Ta có: S = $\frac{1}{2}$( a + b ).h

Khi đó ta có: 

Chọn đáp án B.

Bài 2: Hình thang có độ dài đáy lần lượt là 6cm, 4cm và diện tích hình thang đó là 15cm². Chiều cao hình thang có độ dài là ?

A. 3cm.   

B. 1,5cm

C. 2cm   

D. 1cm

Lời giải:

Diện tích của hình thang là S = $\frac{1}{2}$( a + b ).h

⇒ ( a + b ).h = 2S ⇔ h = $\frac{2S}{\left(a+b\right)}$

Khi đó, chiều cao của hình thang là h = $\frac{(2.15)}{(6 + 4)}$ = 3( cm ).

Chọn đáp án A.

Bài 3: Cho hình bình hành ABCD ( AB//CD ) có AB = CD = 4cm, độ dài đường cao hình bình hành là h = 2cm. Diện tích của hình bình hành là?

A. 4 (cm²)   

B. 8 (cm²)

C. 6 (cm²)   

D. 3 (cm²)

Lời giải:

Ta có : S = a.h

Khi đó ta có: S = 4.2 = 8( cm² ).

Chọn đáp án B.

Bài 4: Cho hình thang vuông ABCD ($\hat{A}=\hat{D}$ = 90⁰ ), trong đó có $\hat{C}$ˆ = 45⁰, AB = 2cm, CD = 4cm. Diện tích của hình thang vuông ABCD là

A. 3 (cm²)   

B. 8 (cm²)

C. 4 (cm²)   

D. 6 (cm²)

Lời giải:

Xét hình thang ABCD

Từ B kẻ BH ⊥ CD, khi đó ta được hình chữ nhật ABHD ⇒ AB = DH = 2cm

⇒ HC = CD - DH = 4 - 2 = 2cm.

+ Xét Δ BDC có BH là đường cao đồng thời là đường trung tuyến

⇒ Δ BDC là tam giác cân tại B.

Mà $\widehat{BCD}$ = 45⁰ ⇒ $\widehat{BDC}$ˆ = 45⁰

⇒ $\widehat{DBC}$ˆ = 180⁰ - ( $\widehat{BCD} + \widehat{BDC}$ˆ ) = 180⁰ - 90⁰ = 90⁰.

⇒ Δ BDC là tam giác vuông cân tại B nên BH = $\frac{1}{2}$DC = 2cm.

Do đó

Chọn đáp án D.

Bài 5: Cho tam giác ABC có BC = 16cm ,đường cao AH = 8cm. Gọi M và N lần lượt là trung điểm của AB và AC. Tính diện tích của tứ giác MNCB?

A. 48cm² 

B. 40cm²

C. 54cm² 

D. 60cm²

Lời giải:

Xét tam giác ABC có M và N lần lượt là trung điểm của AB và AC nên MN là đường trung bình của tam giác ABC.

Suy ra: MN // BC và

Do đó, tứ giác MNCB là hình thang .

Vì AH = 8cm nên đường cao kẻ từ M đến BC bằng

Diện tích hình thang MNCB là :

Chọn đáp án A

Bài 6: Cho tam giác ABC vuông tại A có AB = 6cm và BC = 10cm . Gọi M và N theo thứ tự là trung điểm của AB và BC. Tính diện tích của tứ giác MNCA?

A. 10 cm² 

B. 12cm²

C. 15cm² 

D. 18cm²

Lời giải:

Vì M là trung điểm của AB nên:

Áp dụng định lí py tago vào tam giác ABC có:

BC² = AB² + AC² suy ra: AC² = BC² - AB² = 10² - 6² = 64

Suy ra: AC = 8cm

Xét tam giác ABC có M và N lần lượt là trung điểm của AB và BC nên MN là đường trung bình của tam giác ABC nên: MN// AC và

Suy ra: tứ giác MNCA là hình thang vuông.

Diện tích hình thang MNCA là:

Chọn đáp án D

Bài 7: Cho tam giác ABC có M, N và P lần lượt là trung điểm của AB, AC và P. Biết đường cao AH = 10cm và BC = 16cm . Tính diện tích tứ giác MNPB?

A. 20cm² 

B. 30cm²

C. 40cm² 

D. 50cm²

Lời giải:

Xét tam giác ABC có M và N lần lượt là trung điểm của AB và AC nên MN là đường trung bình của tam giác ABC

Suy ra: MN// BC và

Tương tự, có NP là đường trung bình của tam giác nên: NP // AB

Xét tứ giác MNPB có MN// BC và NP // AB

Suy ra: tứ giác MNPB là bình hành.

Tam giác ABC có đường cao AH = 10cm nên đường cao ứng với cạnh đáy của hình bình hành MNPB là:

Diện tích hình bình hành MNPB là:

Chọn đáp án C

Bài 8: Cho hình bình hành ABCD có diện tích là 40cm². Tính diện tích tam giác ABC?

A. 10cm² 

B. 15cm²

C. 20cm² 

D. 18cm²

Lời giải:

Do ABCD là hình bình hành nên: AB = CD và BC = AD

Xét tam giác ABC và tam giác CDA có :

AB = CD

BC = AD

AC chung

⇒ ΔABC = ΔCDA (c.c.c)

Suy ra: S_ABC = S_CDA

Mà S_ABC + S_CDA = S_ABCD

Do đó

Chọn đáp án C

Bài 9: Cho hình thang ABCD (AB// CD) có AB = 6cm và CD = 10cm. Biết diện tích hình thang ABCD là 60cm². Tính diện tích tam giác ACD?

A. 37,5cm² 

B. 35cm²

C. 30cm² 

D. 40cm²

Lời giải:

Chọn đáp án A

Bài 10: Cho hình thang ABCD có AB// CD; AB = 10cm , CD = 12cm, đường cao AH = 6cm . Gọi M và N lần lượt là trung điểm của AD và BC. Tính diện tích tứ giác ABNM?

A. 30cm² 

B. 29,5cm²

C. 27,5cm² 

D.31,5cm²

Lời giải:

Xét hình thang ABCD có M và N lần lượt là trung điểm của AD và BC nên MN là đường trung bình của hình thang:

Suy ra: MN// AB// CD và

Suy ra: tứ giác MNCD là hình thang.

Vì M là trung điểm của AD và đường cao AH = 6cm nên chiều cao xuất phát từA của hình thang MNCD là:

Diện tích hình thang ABNM là :

Chọn đáp án D

II Bài tập tự luận có lời giải

Bài 1: Cho hình thoi có cạnh là 10 cm, một trong hai đường chéo có độ dài là 16 cm Diện tích của hình thoi là?

Lời giải

Giả sử hình thoi ABCD có đường chéo AC vuông góc BD tại O, AB = 10 cm; AC = 16 cm.

Áp dụng định lý Py-ta-go trong tam giác vuông AOB vuông tại O ta có:

Bài 2 Cho hình thoi ABCD có hai đường chéo AC và BD cắt nhau tại O. Biết AB = 10 cm, OA = 6cm. Diện tích hình thoi ABCD là?

Lời giải

Áp dụng định lý Py-ta-go trong tam giác vuông AOB vuông tại O ta có:

Cho hình thoi ABCD có hai đường chéo AC và BD cắt nhau tại O. Biết AB = 10 cm, OA = 6cm. Diện tích hình thoi ABCD là?

Lời giải

Áp dụng định lý Py-ta-go trong tam giác vuông AOB vuông tại O ta có:

Bài 3 Cho hình thoi ABCD có hai đường chéo AC và BD cắt nhau tại O. Biết AB = 20 cm, OA = 16cm. Diện tích hình thoi ABCD là?

Lời giải

Áp dụng định lý Py-ta-go trong tam giác vuông AOB vuông tại O ta có:

Bài 4 Cho tứ giác ABCD có đường chéo AC vuông góc với BD, diện tích của ABCD là 25 cm²; BD = 5 cm. Độ dài đường chéo AC là?

Lời giải

Bài 5 Vì sao hình chữ nhật ABCD và hình bình hành ABEF (h.141) lại có cùng diện tích? Suy ra cách vẽ một hình chữ nhật có cùng diện tích với một hình bình hành cho trước.

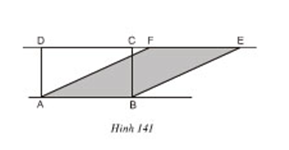
Lời giải:

Hình chữ nhật ABCD và hình bình hành ABEF có đáy chung là AB và có chiều cao bằng nhau, vậy chúng có diện tích bằng nhau.

Suy ra cách vẽ 1 hình chữ nhật có cùng diện tích với 1 hình bình hành cho trước:

- Lấy 1 cạnh của hình bình hành ABEF làm 1 cạnh của hình chữ nhật cần vẽ, chẳng hạn cạnh AB.

- Vẽ đường thẳng EF.

- Từ A và B vẽ các đường thẳng vuông góc với đường thẳng EF chúng cắt đường thẳng EF lần lượt tại D, C. Vẽ các đoạn thẳng AD, BC.

ABCD là hình chữ nhật có cùng diện tích với hình bình hành ABEF đã cho.

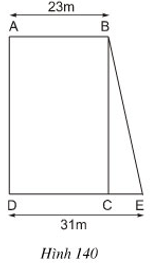
Bài 6 Tính diện tích mảnh đất hình thang ABED theo các độ dài đã cho trên hình 140 và biết diện tích hình chữ nhật ABCD là 828m².

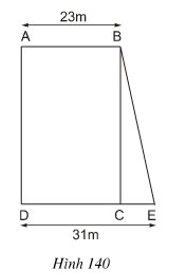
Lời giải:

Ta có: S_ABCD = 828m²

⇔ AD.AB = 828

Mà AB = 23m ⇒ AD = 36m.

Diện tích hình thang ABED là:

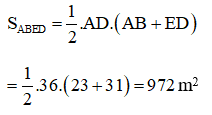
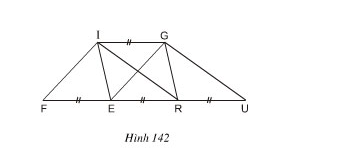
Bài 7 Xem hình 142 (IG // FU). Hãy đọc tên một số hình có cùng diện tích với hình bình hành FIGE.

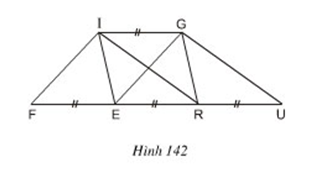
Lời giải:

+ Nhận thấy các hình IGRE và IGUR là hình bình hành.

Gọi h là chiều cao từ I đến cạnh FE, đồng thời là chiều cao từ I đến FU.

⇒ S_IGRE = h.RE

và S_IGUR = h.RU; S_FIGE = h.FE.

Mà FE = RE = RU

⇒ S_FIGE = S_IGRE = S_IGUR.

+ Lại có S_FIGE = h.FE = $\frac{1}{2}$.h.2FE = $\frac{1}{2}$.h.FR = S_FIR

Tương tự S_FIGE = S_GEU

Vậy S_FIGE = S_IGRE = S_IGUR = S_IFR = S_GEU

Bài 8 Khi nối trung điểm của hai đáy hình thang, tại sao ta được hình thang có diện tích bằng nhau?

Lời giải:

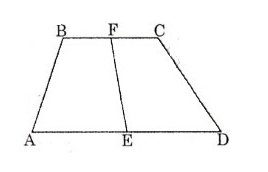
Vẽ hình thang ABCD như hình trên. Gọi E, F lần lượt là trung điểm của 2 đáy AB, CD.

Hai hình thang ABFE và CDEF có:

+ Chung chiều cao

+ Hai đáy nhỏ bằng nhau

+ Hai đáy lớn bằng nhau

⇒ Hai diện tích bằng nhau.

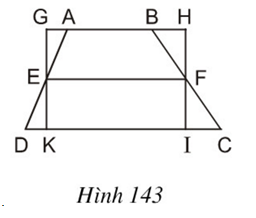
Bài 9 Trên hình 143 ta có hình thang ABCD với đường trung bình EF và hình chữ nhật GHIK. Hãy so sánh diện tích hai hình này, từ đó suy ra một cách chứng minh khác về công thức diện tích hình thang

.

Lời giải:

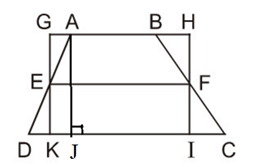
Ta có hình thang ABCD (AB // CD) với đường trung bình EF và hình chữ nhật GHIK như hình vẽ.

Dễ dàng chứng minh:

ΔAEG = ΔDEK, ΔBFH = ΔCFI

Do đó S_ABCD = S_AEKIFB + S_DEK + S_CFI = S_AEKIFB + S_AEC + S_BFH = S_GHIK

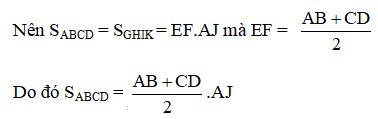
Vậy ta gặp lại công thức tính diện tích hình thang đã học nhưng bằng 1 phương pháp chứng minh khác.

Mặt khác, ta phát hiện công thức mới: Diện tích hình thang bằng tích của đường trung bình hình thang với đường cao.

III Bài tập vận dụng

Bài 1 Trên hình 143 ta có hình thang ABCD với đường trung bình EF và hình chữ nhật GHIK. Hãy so sánh diện tích hai hình này, từ đó suy ra một cách chứng minh khác về công thức diện tích hình thang

.

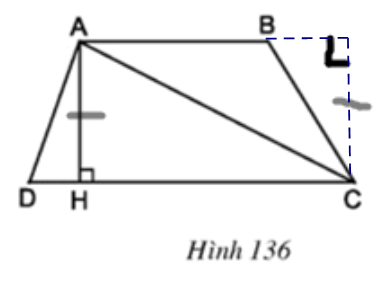
Bài 2 Hãy chia hình thang ABCD thành hai tam giác rồi tính diện tích hình thang theo hai đáy và đường cao (h.136).

Bài 4 Hãy dựa vào công thức tính diện tích hình thang để tính diện tích hình bình hành.

Bài 5 Tính diện tích mảnh đất hình thang ABED theo các độ dài đã cho trên hình 140 và biết diện tích hình chữ nhật ABCD là 828m².

Bài 6 Vì sao hình chữ nhật ABCD và hình bình hành ABEF (h.141) lại có cùng diện tích? Suy ra cách vẽ một hình chữ nhật có cùng diện tích với một hình bình hành cho trước.

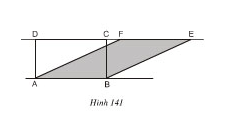
Bài 7 Xem hình 142 (IG // FU). Hãy đọc tên một số hình có cùng diện tích với hình bình hành FIGE.

Bài 8 Khi nối trung điểm của hai đáy hình thang, tại sao ta được hai hình thang có diện tích bằng nhau?

Bài 9 Tính diện tích mảnh đất hình thang ABED theo các độ dài cho trên hình vẽ và biết diện tích hình chữ nhật ABCD là 828 cm${}^2$

Bài 10 Tính diện tích hình bình hành ABCD biết AD = 6cm, AB = 10cm và 

Bài 11 Tính diện tích hình thang vuông ABCD ($\hat{A}=\hat{D}={90}^{\circ }$), biết $\hat{C}={45}^{\circ }$, AB = 2cm và CD = 4cm.

Bài 12 Tính diện tích hình thang ABCD biết AB = 3cm, BC = 8cm, CD = 12cm và $\hat{C}={30}^{\circ }$

Bài 13 Cho hình thang cân ABCD (AB // CD, AB < CD) biết chiều cao AH = 8cm và HC = 12cm.

Bài 14 Chứng minh rằng diện tích tam giác có cạnh đáy là cạnh bên của hình thang là trung điểm của cạnh bên kia thì bằng một nửa diện tích của hình thang đó.

Bài 15 Tính diện tích hình bình hành biết hai cạnh kề bằng 6cm và 9cm, góc xen giữa bằng 120${}^{\circ }$

Bài 16 Cho hình thang ABCD (AB // CD). Gọi E là trung điểm của BC kẻ EH vuông góc với AD. Chứng minh rằng $S_{ABCD}$ = AB.EH

Bài 17 Cho hình bình hành ABCD. Trên cạnh AB lấy điểm M, trong hình bình hành ABCD lấy điểm N. Chứng minh rằng:

a) $S_{MCD}=\frac{1}{2}{S}_{ABCD}$

b) $S_{ABN}+S_{CDN}=\frac{1}{2}{S}_{ABCD}$

B. Lý thuyết Diện tích hình thang.

1. Công thức diện tích của hình thang

Diện tích hình thang bằng một nửa tích của tổng hai đáy với chiều cao.

Ta có: S = 1/2( a + b ).h

Lý thuyết tính diện tích hình thang: Muốn tính diện tích hình thang ta cộng tổng hai đáy rồi nhân với chiều cao, sau đó chia đôi.

Ví dụ: Cho hình thang ABCD ( AB//CD ) có AB = 3cm; CD = 5cm, chiều cao hình thang là h = 4cm. Tính diện tích hình thang ?

Hướng dẫn:

Diện tích hình thang cần tìm là S_ABCD = 1/2( AB + CD ).h = 1/2( 3 + 5 ).4 = 16( cm² )

2. Công thức tính diện tích hình bình hành

Ta có : S = a.h

Ví dụ: Cho hình bình hành ABCD ( AB//CD ) có AB = CD = 5cm, độ dài đường cao hình bình hành là h = 4cm. Tính diện tích của hình bình hành?

Hướng dẫn:

Diện tích hình hình hành là S_ABCD = AB.h = 4.5 = 20( cm² )