Tailieumoi.vn xin giới thiệu Bài tập Toán 8 Chương 2 Bài 1: Đa giác. Đa giác đều. Bài viết gồm 50 bài tập với đầy đủ các mức độ và có hướng dẫn giải chi tiết sẽ giúp học sinh ôn luyện kiến thức và rèn luyện kĩ năng làm bài tập Toán 8. Ngoài ra, bài viết còn có phần tóm tắt nội dung chính lý thuyết Chương 2 Bài 1:Đa giác. Đa giác đều. Mời các bạn đón xem:

Bài tập Toán 8 Chương 2 Bài 1: Đa giác. Đa giác đều

A. Bài tập Đa giác. Đa giác đều

I. Bài tập trắc nghiệm

Bài 1: Trong các khẳng định sau, khẳng định nào đúng, khẳng định nào sai ?

A. Hình vuông là đa giác đều.

B. Tổng các góc của đa giác lồi 8 cạnh là 1080⁰.

C. Hình thoi là đa giác đều.

D. Số đo góc của hình bát giác đều là 135,5⁰.

Lời giải:

Ta cần nhớ định nghĩa: Đa giác đều là đa giác có tất cả các cạnh bằng nhau và tất cả các góc bằng nhau.

+ Hình vuông là hình có 4 cạnh bằng nhau và 4 góc bằng nhau

⇒ Hình vuông là đa giác đều.

⇒ Đáp án A đúng.

+ Hình thoi là hình có 4 cạnh bằng nhau nhưng 4 góc không bằng nhau.

⇒ Hình thoi không phải là đa giác đều.

⇒ Đáp án C sai.

+ Tổng số đo các góc của đa giác n cạnh là ( n - 2 ).180⁰.

Khi đó tổng các góc của đa giác lồi 8 cạnh là ( 8 - 2 ).180⁰ = 1080⁰.

⇒ Đáp án B đúng.

+ Số đo của một góc của đa giác đều n cạnh là $\frac{\left(\right( n - 2 ).{180}^0)}{n}$.

Khi đó số đo của hình bát giác đều là $\frac{\left(\right( 8 - 2 ).{180}^0)}{8}$ = 135⁰.

⇒ Đáp án D sai.

Bài 2: Một đa giác 7 cạnh thì số đường chéo của đa giác đó là ?

A. 12.   

B. 13.

C. 14.   

D. Kết quả khác.

Lời giải:

Số đường chéo của đa giác n cạnh là $\frac{\left(n\right( n - 3 \left)\right)}{2}$

Khi đó số đường chéo của đa giác 7 cạnh là $\frac{\left(7\right( 7 - 3 \left)\right)}{2}$ = 14 (đường chéo)

Chọn đáp án C.

Bài 3: Một đa giác có số đường chéo bằng số cạnh của đa giác thì đa giác có số cạnh là?

A. 5.   

B. 6.

C. 4.   

D. 7.

Lời giải:

Số đường chéo của đa giác n cạnh là $\frac{\left(n\right( n - 3 \left)\right)}{2}$. ( n ∈ N, n ≥ 3 )

Theo giả thiết ta có $\frac{\left(n\right( n - 3 \left)\right)}{2}$ = n ⇔ n(n - 3 ) = 2n ⇔ n² - 3n - 2n = 0

⇔ n² - 5n = 0 ⇔ n( n - 5 ) = 0 ⇔ 

So sánh điều kiện ta có n = 5 thỏa mãn.

Bài 4: Tổng số đo các góc của đa giác 12 cạnh là?

A. 1800^o    

B. 1600^o

C. 1720^o    

D. 1440^o

Lời giải:

Tổng số đo các góc của đa giác n cạnh là (n -2).180^o

Do đó, Tổng số đo các góc của đa giác 12 cạnh là (12 – 2).180^o = 1800^o

Chọn đáp án A

Bài 5: Số đường chéo xuất phát từ 1 đỉnh của đa giác 20 cạnh là?

A. 15    

B. 16

C. 17    

D. 18

Lời giải:

Số đường chéo xuất phát từ 1 đỉnh của đa giác n cạnh là n – 3

Do đó, Số đường chéo xuất phát từ 1 đỉnh của đa giác 20 cạnh là: 20 – 3 = 17

Chọn đáp án C

Bài 6: Số đường chéo của đa giác 10 cạnh?

A. 50    

B. 60

C. 70    

D. 80

Lời giải:

Số đường chéo xuất phát từ 1 đỉnh của đa giác 10 cạnh là: 10 – 3 = 7

Suy ra: số đường chéo của đa giác 10 cạnh là: 7.10 = 70 đường chéo

Chọn đáp án B

Bài 7: Số đo mỗi góc của 10- giác đều là:

A. 100^o    

B. 120^o

C. 136^o    

D. 144^o

Lời giải:

Tổng số đo các góc của 10 – giác đều là: (10 - 2). 180^o = 1440^o

Do đây là 10 – giác đều nên số đo các góc bằng nhau và bằng: 144^o: 10 = 144^o

Chọn đáp án D

Bài 8: Cho đa giác đều n cạnh. Biết số đo mỗi góc bằng 140^o. Tìm n?

A. n = 9    

B. n = 8

C. n = 7    

D. n = 10

Lời giải:

Tổng số đo các góc của đa giác n cạnh là: 140.n

Mặt khác đa giác n cạnh thì có tổng số đo các góc của đa giác là: (n-2). 180

Suy ra: 140n = (n – 2). 180

⇔ 140n = 180n - 360

⇔ 40n = 360 ⇔ n = 9

Chọn đáp án A

Bài 9: Cho đa giác đều 11 cạnh có độ dài mỗi cạnh là 5cm. Tính chu vi đa giác

A. 45cm    

B. 50cm

C. 60cm    

D. 55cm

Lời giải:

Chu vi của đa giác đều 11 cạnh là: 5.11 = 55 cm

Chọn đáp án D

Bài 10: Hình vuông có mấy trục đối xứng?

A. 1    

B. 2

C. 3    

D. 4

Lời giải:

Hình vuông có 4 trục đối xứng bao gồm:

+ 2 đường chéo của hình vuông

+ 2 đường thẳng đi qua tâm và song song với 2 cạnh của hình vuông

Chọn đáp án D

II Bài tập tự luận có lời giải

Bài 1: Một đa giác có số đường chéo là 44 thì có số cạnh là:

Lời giải:

Số cạnh của đa giác là 12

Số cạnh của đa giác là 11

Đáp án cần chọn là: A

Bài 2: Cho các hình: Hình chữ nhật, hình thoi, hình vuông, tam giác cân, tam giác đều.

Lời giải:

Hình vuông là tứ giác đều (có bốn cạnh bằng nhau và các góc cùng bằng 90⁰) và tam giác đều là những đa giác đều.

Hình chữ nhật là đa giác không đều vì hình chữ nhật có 4 góc vuông nhưng các cạnh không bằng nhau nên không là đa giác đều.

Hình thoi là đa giác không đều vì các cạnh bằng nhau nhưng các góc không bằng nhau.

Tam giác cân không là đa giác đều vì có ba cạnh không bằng nhau

Bài 3: Chọn câu đúng

A. Lục giác có sáu góc bằng nhau là lục giác đều.                            

B. Hình thoi là đa giác không đều có các góc bằng nhau.

C. Ngũ giác có năm cạnh bằng nhau được gọi là ngũ giác đều.                                

D. Hình chữ nhật là đa giác không đều có các góc bằng nhau.

Lời giải

Hình chữ nhật là đa giác không đều vì hình chữ nhật có 4 góc vuông nhưng các cạnh không bằng nhau nên không là đa giác đều.

Hình thoi là đa giác không đều vì các cạnh bằng nhau nhưng các góc không bằng nhau.

Bài 4: Cho ABCDEF là hình lục giác đều. Hãy chọn câu sai:

A. ABCDEF có một tâm đối xứng                

B. Mỗi góc trong của nó là 120⁰.

C. Tổng các góc trong của nó là 720⁰.                                  

D. Mỗi góc trong của nó là 150⁰.

Lời giải

Số cạnh của đa giác là 12

Câu sai là: Mỗi góc trong của nó là 150⁰.

Bài 5: Cho ABCDEF là hình ngũ giác đều. Hãy chọn câu sai:

A. ABCDEF có một tâm đối xứng                

B. Mỗi góc trong của nó là 108⁰.

C. Tổng các góc trong của nó là 450⁰.                                  

D. Tổng các góc trong của nó là 540⁰.

Lời giải

Số cạnh của đa giác là 12

Câu sai là: Tổng các góc trong của nó là 450⁰.

Bài 6 Tại sao hình gồm năm đoạn thẳng AB, BC, CD, DE, EA ở hình 118 không phải là đa giác?

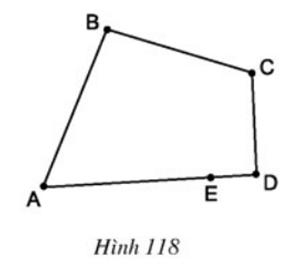
Lời giải

Hình 118 không phải là một đa giác vì DE và EA cùng nằm trên một đường thẳng

Bài 7 Tại sao các đa giác ở hình 112, 113, 114 không phải là đa giác lồi?

Lời giải

- Hình 112: Đa giác nằm trên hai nửa mặt phẳng có bờ AB (hoặc bờ DE, hoặc bờ DC)

- Hình 113: Đa giác nằm trên hai nửa mặt phẳng có bờ BC (hoặc bờ CD)

- Hình 114: Đa giác nằm trên hai nửa mặt phẳng có bờ AB/ BC/ CD/ DE/ EA

Bài 8 Quan sát đa giác ABCDEG ở hình 119 rồi điền vào chỗ trống trong các câu sau:

Các đỉnh là các điểm: A, B, …

Các đỉnh kề nhau là: A và B, hoặc B và C, hoặc …

Các cạnh là các đoạn thẳng: AB, BC, …

Các đường chéo là các đoạn thẳng nối hai đỉnh không kề nhau: AC, CG, …

Các góc là: $\hat{A}$ , $\hat{B}$ , …

Các điểm nằm trong đa giác (các điểm trong của đa giác) là: M, N, …

Các điểm nằm ngoài đa giác (các điểm ngoài của đa giác) là: Q, …

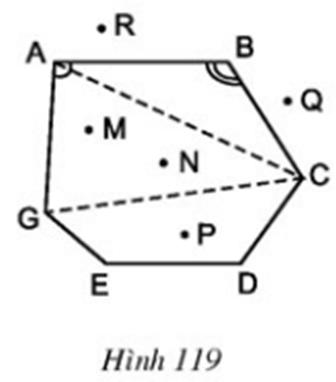
Lời giải

Các đỉnh là các điểm: A, B, C, D, E, G

Các đỉnh kề nhau là: A và B, hoặc B và C, hoặc C và D, hoặc D và E, hoặc E và G, hoặc G và A

Các cạnh là các đoạn thẳng: AB, BC, CD, DE, EG, GA

Các đường chéo là các đoạn thẳng nối hai đỉnh không kề nhau: AC, CG, AD, AE, BG, BE, BD, CE, DG

Các góc là: $\hat{A}, \hat{B}, \hat{C}, \hat{D}, \hat{E}, \hat{G}$

Các điểm nằm trong đa giác (các điểm trong của đa giác) là: M, N, P

Các điểm nằm ngoài đa giác (các điểm ngoài của đa giác) là: Q, R

Bài 9 Hãy vẽ các trục đối xứng và tâm đối xứng của mỗi hình 120a, b, c, d (nếu có)

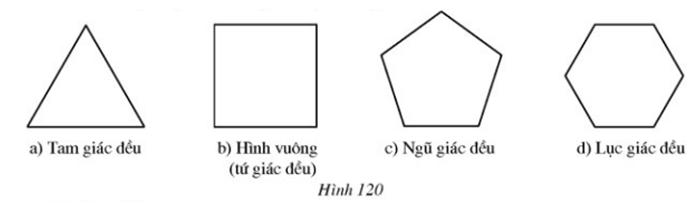
Lời giải

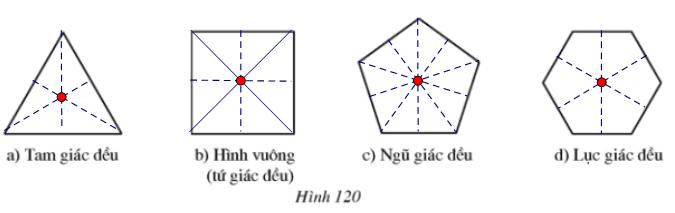
a) Trục đối xứng là các đường trung trực của tam giác đều

Tâm đối xứng là giao điểm ba đường trung trực

b) Trục đối xứng là đường thẳng nối hai trung điểm của hai cạnh đối nhau của hình vuông và hai đường chéo

Tâm đối xứng là giao điểm hai đường chéo

c) Trục đối xứng là đường thẳng nối đỉnh và trung điểm cạnh đối diện đỉnh đó

Tâm đối xứng là giao điểm của các trục đối xứng

d) Trục đối xứng là đường thẳng nối hai trung điểm của hai cạnh đối nhau của lục giác đều

Tâm đối xứng là giao điểm của các trục đối xứng

Bài 10 Hãy vẽ phác một lục giác lồi.

Hãy nêu cách nhận biết một đa giác lồi.

Lời giải:

- Lục giác lồi ABCDEF

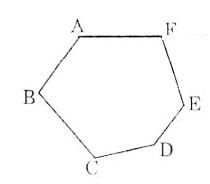
- Cách nhận biết một đa giác lồi: Một đa giác lồi là một đa giác thỏa mãn điều kiện sau:

+ Các cạnh chỉ cắt nhau tại các đỉnh, nghĩa là không có hai cạnh nào cắt nhau tại một điểm mà không phải là đỉnh. Một đa giác thỏa mãn điều kiện này là đa giác đơn.

+ Đa giác luôn nằm trong một nửa mặt phẳng mà bờ là đường thẳng chứa một cạnh tùy ý của nó. Một đa giác đơn thỏa mãn thêm điều kiện này là một đa giác lồi.

III. Bài tập vận dụng

Bài 1 Cho ví dụ về đa giác không đều trong mỗi trường hợp sau:

a) Có tất cả các cạnh bằng nhau.

b) Có tất cả các góc bằng nhau.

Bài 2 Cho hình thoi ABCD có góc $\hat{A}$ = 60^o. Gọi E, F, G, H lần lượt là trung điểm của các cạnh AB, BC, CD, DA. Chứng minh rằng đa giác EBFGDH là lục giác đều.

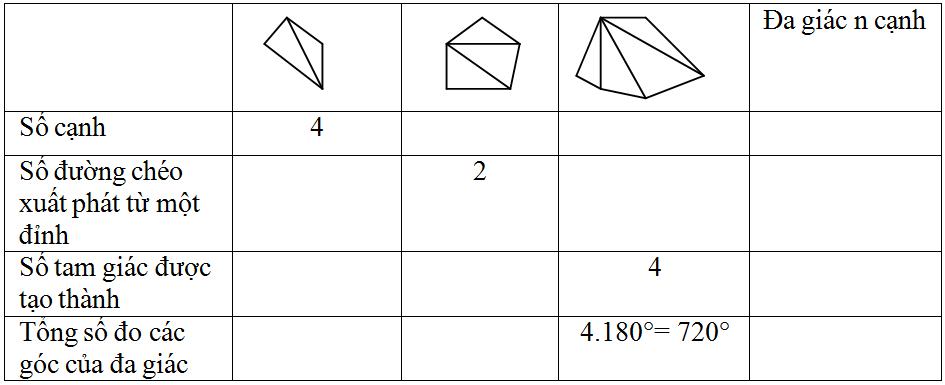
Bài 3 Điền số thích hợp vào các ô trống trong bảng sau:

Bài 4 Tính số đo mỗi góc của ngũ giác đều, lục giác đều, n – giác đều.

Bài 5 Cho hình bình hành ABCD có diện tích 60cm. Gọi M, N lần lượt là trung điểm của BC, CD và I là giao điểm của BN, DM. Tính diện tích tứ giác ABID.

Bài 6 Cho ABC và điểm D thuộc cạnh BC. Qua D hãy dựng một đường thẳng chia tam giác thành hai phần có diện tích bằng nhau.

Bài 7 Chứng minh công thức tính diện tích tam giác S = p.r trong đó p là nửa chu vi và r là khoảng cách từ giao điểm của ba đường phân giác đến mỗi cạnh.

Bài 8 Ở một sàn giao dịch bất động sản, người ta quảng cáo bán một hồ hình tam giác và ba mảnh đất hình vuông dựng trên ba cạnh hồ. Diện tích ba mảnh đất đó thứ tự bằng 74ha, 116 ha và 370 ha. Bảng quảng cáo không nói rõ diện tích của hồ, làm nhiều người thắc mắc, không rõ diện tích hồ lớn hay bé. Bạn hãy tính giúp xem diện tích của hồ bằng bao nhiêu?

Bài 9 Cho lục giác ABCDEF có các cạnh đối diện AB và DE, BC và EF, CD và FA đôi một song song với nhau. Chứng minh rằng $S_{ACE}=S_{BDE}$

Bài 10 Cho $\mathrm{\Delta }$ABC và điểm D thuộc cạnh BC. Qua D hãy dựng hai đường thẳng chia $\mathrm{\Delta }$ABC thành ba phần có diện tích bằng nhau.

Bài 11 Cho tứ giác ABCD và điểm E thuộc cạnh AB (diện tích $\mathrm{\Delta }$ADE, $\mathrm{\Delta }$BCE nhỏ hơn nửa diện tích tứ giác). Hãy dựng một đường thẳng đi qua E chia tứ giác đã cho thành hai phần có diện tích bằng nhau.

B. Lý thuyết Đa giác. Đa giác đều

1. Khái niệm về đa giác

Định nghĩa: Đa giác lồi là đa giác luôn nằm trong một nửa mặt phẳng mà bờ là đường thẳng chứa bất kì cạnh nào của đa giác đó.

 

Chú ý: Từ nay nếu nhắc đến đa giác thì ta quy ước đó là đa giác lồi

2. Đa giác đều

Đa giác đều là đa giác có tất cả các cạnh bằng nhau và tất cả các góc bằng nhau.

  

3. Mở rộng

a) Góc trong đa giác

+ Tổng số đo các góc của đa giác n cạnh là ( n - 2 ).180⁰.

+ Số đo của một góc của đa giác đều n cạnh là

b) Số đường chéo của đa giác n cạnh

Số đường chéo của đa giác n cạnh là

Ví dụ: Cho một đa giác đều có 20 cạnh. Tính số đo một góc và số đường chéo của đa giác đều đó ?

Hướng dẫn:

+ Số đo của một góc của đa giác đều n cạnh là

Khi đó số đo của một góc của đa giác đều 20 cạnh là:

+ Số đường chéo của đa giác n cạnh là

Khi đó số đường chéo của đa giác đều 20 cạnh là