Tailieumoi.vn xin giới thiệu Giải bài tập Toán 8 Bài 1: Đa giác. Đa giác đều hay, chi tiết giúp học sinh dễ dàng làm bài tập Đa giác. Đa giác đều lớp 8.

Giải bài tập Toán lớp 8 Bài 1: Đa giác. Đa giác đều

Trả lời câu hỏi giữa bài

Câu hỏi 1 trang 114 Toán 8 Tập 1:Tại sao hình gồm năm đoạn thẳng AB, BC, CD, DE, EA ở hình 118 không phải là đa giác?

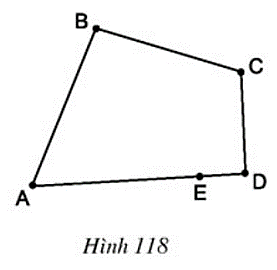
Lời giải

Hình 118 không phải là một đa giác vì DE và EA cùng nằm trên một đường thẳng

Câu hỏi 2 trang 114 Toán 8 Tập 1:Tại sao các đa giác ở hình 112, 113, 114 không phải là đa giác lồi?

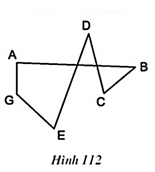
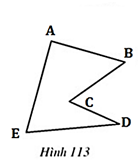
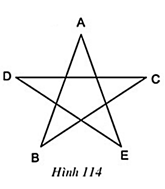
Lời giải

- Hình 112: Đa giác nằm trên hai nửa mặt phẳng có bờ AB (hoặc bờ DE, hoặc bờ DC)

- Hình 113: Đa giác nằm trên hai nửa mặt phẳng có bờ BC (hoặc bờ CD)

- Hình 114: Đa giác nằm trên hai nửa mặt phẳng có bờ AB (hoặc bờ BC, hoặc bờ CD, hoặc bờ DE, hoặc bờ EA)

Câu hỏi 3 trang 114 Toán 8 Tập 1:Quan sát đa giác ABCDEG ở hình 119 rồi điền vào chỗ trống trong các câu sau:

Các đỉnh là các điểm: A, B, …

Các đỉnh kề nhau là: A và B, hoặc B và C, hoặc …

Các cạnh là các đoạn thẳng: AB, BC, …

Các đường chéo là các đoạn thẳng nối hai đỉnh không kề nhau: AC, CG, …

Các góc là: $\widehat{A},\widehat{B}$, …

Các điểm nằm trong đa giác (các điểm trong của đa giác) là: M, N, …

Các điểm nằm ngoài đa giác (các điểm ngoài của đa giác) là: Q, …

Lời giải

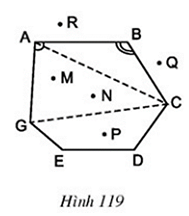
Các đỉnh là các điểm: A, B, C, D, E, G

Các đỉnh kề nhau là: A và B, hoặc B và C, hoặc C và D, hoặc D và E, hoặc E và G, hoặc G và A

Các cạnh là các đoạn thẳng: AB, BC, CD, DE, EG, GA

Các đường chéo là các đoạn thẳng nối hai đỉnh không kề nhau: AC, CG, AD, AE, BG, BE, BD, CE, DG

Các góc là: $\widehat{A},\widehat{B},\widehat{C},\widehat{D},\widehat{E},\widehat{G}$

Các điểm nằm trong đa giác (các điểm trong của đa giác) là: M, N, P

Các điểm nằm ngoài đa giác (các điểm ngoài của đa giác) là: Q, R

Câu hỏi 4 trang 115 Toán 8 Tập 1:Hãy vẽ các trục đối xứng và tâm đối xứng của mỗi hình 120a, b, c, d (nếu có)

Hình 120

Lời giải

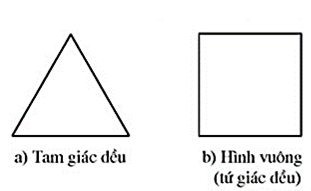
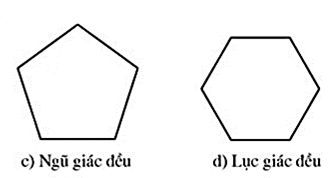
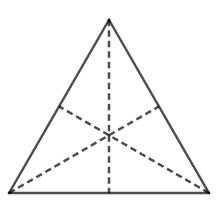
a) Tam giác đều có 3 trục đối xứng là các đường trung trực của tam giác đều.

Tam giác đều không có tâm đối xứng.

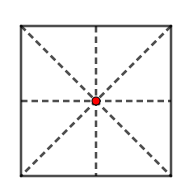
b) Hình vuông có 4 trục đối xứng là hai đường thẳng nối hai trung điểm của hai cạnh đối nhau của hình vuông và hai đường chéo.

Tâm đối xứng là giao điểm hai đường chéo của hình vuông.

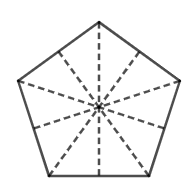
c) Hình ngũ giác đều có 5 trục đối xứng là các đường thẳng nối đỉnh và trung điểm cạnh đối diện đỉnh đó.

Hình ngũ giác đều không có tâm đối xứng.

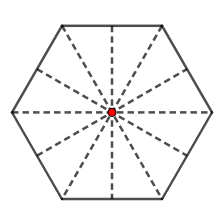
d) Lục giác đều là hình có 6 trục đối xứng gồm ba đường thẳng nối hai trung điểm của hai cạnh đối nhau của lục giác đều và ba đường chéo chính của lục giác đều.

Tâm đối xứng là giao điểm của các trục đối xứng.

Bài tập (trang 115)

Bài 1 trang 115 Toán 8 Tập 1:Hãy vẽ phác một lục giác lồi.

Hãy nêu cách nhận biết một đa giác lồi.

Lời giải:

- Lục giác lồi ABCDEF:

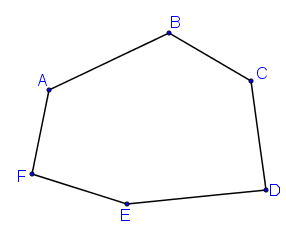
- Cách nhận biết một đa giác lồi:

Lần lượt xét các nửa mặt phẳng bờ là cạnh của đa giác, nếu đa giác luôn nằm hoàn toàn trong một nửa mặt phẳng thì đa giác là đa giác lồi.

Nếu có 1 cạnh mà đa giác nằm trên cả hai nửa mặt phẳng mà đường thẳng chứa cạnh là bờ thì đa giác không phải đa giác lồi.

Bài 2 trang 115 Toán 8 Tập 1:Cho ví dụ về đa giác không đều trong mỗi trường hợp sau:

a) Có tất cả các cạnh bằng nhau.

b) Có tất cả các góc bằng nhau.

Lời giải:

a) Hình thoi có tất cả các cạnh bằng nhau nhưng các góc không bằng nhau nên hình thoi không phải là đa giác đều.

b) Hình chữ nhật có tất cả các góc bằng nhau nhưng các cạnh có thể không bằng nhau nên hình chữ nhật không buộc phải là đa giác đều.

Bài 3 trang 115 Toán 8 Tập 1:Cho hình thoi ABCD có góc $\widehat{A}=60°$. Gọi E, F, G, H lần lượt là trung điểm của các cạnh AB, BC, CD, DA. Chứng minh rằng đa giác EBFGDH là lục giác đều.

Lời giải:

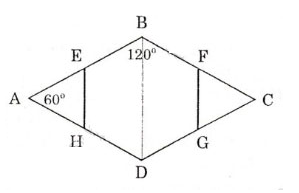
Ta có: $AE=EB=\frac{AB}{2}$ (E là trung điểm của AB)

$BF=FC=\frac{BC}{2}$ (F là trung điểm của BC)

$CG=GD=\frac{CD}{2}$ (G là trung điểm của CD)

$AH=HD=\frac{AD}{2}$ (H là trung điểm của AD)

Vì ABCD là hình thoi nên AB = BC = CD = AD

Suy ra BE = AE = BF = FC = CG = GD = AH = HD = $\frac{AB}{2}$. (1)

Xét $\Delta ABD$, có: BA = DA nên $\Delta ABD$ cân tại A

Mà $\widehat{A}=60°$

Suy ra $\Delta ABD$ đều

$\Rightarrow AB=BD=AD$

Ta lại có:

E là trung điểm của AB

H là trung điểm của AD

Suy ra EH là đường trung bình của

$\Rightarrow EH=\frac{BD}{2}=\frac{AB}{2}$ (2)

Xét $\Delta CBD$, có: BC = CD nên $\Delta CBD$ cân tại C

Mà $\widehat{C}=\widehat{A}=60°$(tính chất hình thoi)

Suy ra $\Delta CBD$ đều

$\Rightarrow CB=BD=CD$

Ta lại có: 

F là trung điểm của CB

G là trung điểm của CD

Suy ra FG là đường trung bình của $\Delta CBD$

$\Rightarrow FG=\frac{BD}{2}=\frac{AB}{2}$ (3)

Từ (1), (2) và (3) suy ra:

BE = AE = BF = FC = CG = GD = AH = HD = EH = FG

Hay EB = BF = FG = GD = DH = HE.

Vì ABCD là hình thoi nên AD // BC

$\begin{array}{l}\Rightarrow \widehat{A}+\widehat{ABC}=180°\\ \iff 60°+\widehat{ABC}=180°\\ \iff \widehat{ABC}=180°-60°=120°\\ \Rightarrow \widehat{ADC}=\widehat{ABC}=120°\end{array}$ 

(tính chất hình thoi) (4)

Vì EH là đường trung bình của $\Delta ABD$(cmt)

$\Rightarrow EH//BD$

$\Rightarrow \widehat{BEH}+\widehat{EBD}=180°$(hai góc trong cùng phía bù nhau)

Mà $\widehat{EBD}=60°$ (Do $\Delta ABD$ đều)

$\Rightarrow \widehat{BEH}=120°$

Chứng minh tương tự ta được: $\widehat{DHE}=\widehat{BFG}=\widehat{FGD}=120°$

Do đó $\widehat{BEH}=\widehat{DHE}=\widehat{BFG}=\widehat{FGD}=120°$(5)

Từ (4) và (5) suy ra: $\widehat{ABC}=\widehat{ADC}=\widehat{BEH}=\widehat{DHE}$$=\widehat{BFG}=\widehat{FGD}=120°$

Vậy EBFGDH có tất cả các góc bằng nhau và tất cả các cạnh bằng nhau nên là lục giác đều.

Bài 4 trang 115 Toán 8 Tập 1:Điền số thích hợp vào các ô trống trong bảng sau:

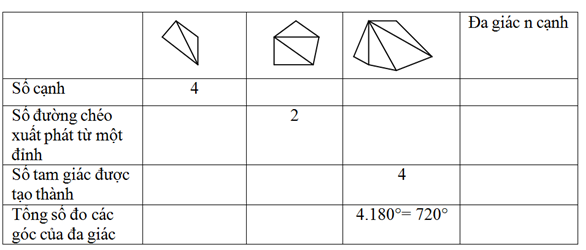
Lời giải:

Ta có bảng sau:

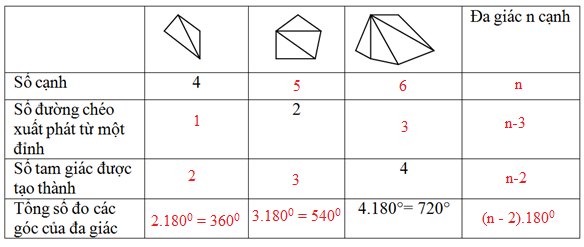
Bài 5 trang 115 Toán 8 Tập 1:Tính số đo mỗi góc của ngũ giác đều, lục giác đều, n – giác đều.

Lời giải:

Từ bài 4, ta có:

Tổng số đó các góc của đa giác n cạnh là: (n – 2).180⁰.

Suy ra số đo mỗi góc của hình n – giác đều là: $\frac{\left(n-2\right).180°}{n}$.

Áp dụng công thức trên, ta có:

Với n = 5 số đo mỗi góc của ngũ giác đều là: $\frac{\left(5-2\right).180°}{5}={108}^0.$

Với n = 6 số đo mỗi góc của lục giác đều là: $\frac{\left(6-2\right).180°}{6}={120}^0.$

Vậy số đo mỗi góc của ngũ giác đều là 108⁰, số đo mỗi góc của lục giác đều là 120⁰, số đo mỗi góc của n giác đều là $\frac{\left(n-2\right).180°}{n}.$