Tailieumoi.vn xin giới thiệu Bài tập Toán 11 Chương 1 Bài 3: Phép đối xứng trục. Bài viết gồm 50 bài tập với đầy đủ các mức độ và có hướng dẫn giải chi tiết sẽ giúp học sinh ôn luyện kiến thức và rèn luyện kĩ năng làm bài tập Toán 11. Ngoài ra, bài viết còn có phần tóm tắt nội dung chính lý thuyết Chương 1 Bài 3: Phép đối xứng trục. Mời các bạn đón xem:
Bài tập Toán 11 Chương 1 Bài 3: Phép đối xứng trục
A. Bài tập Phép đối xứng trục
I. Bài tập trắc nghiệm
Bài 1: Trong mặt phẳng, hình nào sau đây có trục đối xứng?
A. hình thang vuông
B. hình bình hành
C. hình tam giác vuông không cân
D. hình tam giác cân
Đáp án: D
Tam giác cân có trục đối xứng là đường cao (cúng là trung trực, phân giác).
Bài 2: Trong mặt phẳng, cho hình thang cân ABCD có AD = BC. Tìm mệnh đề đúng :
A. có phép đối xứng trục biến thành nên
B. có phép đối xứng trục biến thành nên
C. có phép đối xứng trục biến AB thành CD nên AB // CD
D. có phép đối xứng trục biến DA thành CB nên DA = CB
Đáp án: D
Bài 3: Trong mặt phẳng cho hai đường thẳng a và b tạo với nhau góc 600. Có bao nhiêu phép đối xứng trục biến a thành b.
A. một
B. hai
C. ba
D. bốn
Đáp án: B
Hai đường phân giác của góc tạo bởi a và b.
Nhận xét: Giả thiết góc 600 chỉ để gây nhiễu
Bài 4: Cho hình vuông ABCD tâm I. gọi E, F, G, H lần lượt là trung điểm của các cạnh DA, AB, BC, CD. Phép đối xứng trục AC biến:
A. ∆IED thành ∆IGC
B. ∆IFB thành ∆IGB
C. ∆IBG thành ∆IDH
D. ∆IGC thành ∆IFA
Đáp án: C
Tìm ảnh của từng điểm qua phép đối xứng trục AC: điểm I biến thành I; B thành D; G thành H. Chọn đáp án C
Bài 5: Trong mặt phẳng Oxy cho điểm M(-1;3). Phép đối xứng trục Ox biến M thành M’ thì tọa độ M’ là:
A. M’(-1;3)
B. M’(1;3)
C. M’(-1;-3)
D. M’(1;-3)
Đáp án: C
(x' = x; y' = -y). Chọn đáp án C
Bài 6: Trong mặt phẳng Oxy cho đường thẳng d có phương trình : x - 2y + 4 = 0. Phép đối xứng trục Ox biến d thành d’ có phương trình:
A. x - 2y + 4 = 0
B. x + 2y + 4 = 0
C. 2x + y + 2 = 0
D. 2x - y + 4 = 0
Đáp án: B
Phép đối xứng trục Ox có
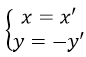
thay vào phương trình d được x'+ 2y' + 4 = 0 hay x + 2y + 4 = 0. Chọn đáp án B
Bài 7: Trong mặt phẳng Oxy cho đường tròn (C) có phương trình:
(x - 3)2 + (y - 1)2 = 6. Phép đối xứng trục Oy biến (C) thành (C’) có phương trình
A. (x + 3)2 + (y - 1)2 = 36
B. (x + 3)2 + (y - 1)2 = 6
C.(x - 3)2 + (y + 1)2 = 36
D. (x + 3)2 + (y + 1)2 = 6
Đáp án: B
Phép đối xứng trục Oy biến tâm I(3;1) của (C) thành I’(-3;1); bán kính không thay đổi. Chọn đáp án B.
Bài 8: Trong mặt phẳng Oxy cho điểm M(2;3). Điểm M là ảnh của điểm nào trong bốn điểm sau qua phép đối xứng trục Oy?
A. A(3;2)
B. B(2; -3)
C. C(3;-2)
D. D(-2;3)
Đáp án: D
Bài 9: Trong các mệnh đề sau mệnh đề nào đúng?
A. Tam giác đều có vô số trục đối xứng
B. Một hình có vô số trục đối xứng thì hình đó phải là đường tròn
C. Hình gồm hai đường thẳng vuông góc có vô số trục đối xứng
D. Hình tròn có vô số trục đối xứng
Đáp án: D
Phương án A. Tam giác đều chỉ có ba trục đối xứng là ba đường cao.
Phương án B. Đường thẳng cũng có vô số trục đối xứng (là đường thẳng bất kì vuông góc với đường thẳng đã cho).
Phương án C. Hình gồm hai đường thẳng vuông góc có bốn trục đối xứng (là chính hai đường thẳng đó và hai đường phân giác của góc tạo bởi hai đường thẳng đó).
Bài 10: Trong mặt phẳng, hình vuông có mấy trục đối xứng?
A. một
B. hai
C. ba
D. bốn
Đáp án: D
Hai đường chéo và hai đường trung bình.
II. Bài tập tự luận có lời giải
Bài 1: Trong mặt phẳng Oxy cho đường thẳng d có phương trình 2x - 8y + 11 = 0. Phép đối xứng trục Oy biến d thành d’ có phương trình?
Lời giải:
Phép đối xứng trục Oy có:
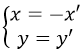
Thay vào phương trình d ta được -2x' - 8y' + 11 = 0 hay 2x + 8y - 11 = 0
Bài 2: Trong mặt phẳng Oxy cho đường thẳng d có phương trình x-2y+2=0 và đường thằng l có phương trình : x - y + 1 = 0. Phép đối xứng trục l biến d thành d’ có phương trình
Lời giải:
Gọi giao điểm của d và l là điểm I. Tọa độ điểm I là nghiệm hệ:
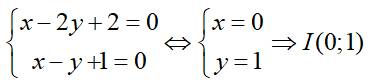
Lấy A(4; 3) thuộc d. Phương trình đường thẳng a qua A và vuông góc với đường thẳng l có vecto chỉ phương là: = = (1;-1) nên có vecto pháp tuyến là: = (1;1)
Phương trình đường thẳng a: 1( x – 4) + 1.(y – 3) =0 hay x + y – 7 = 0
Gọi H là giao điểm của a và l.Tọa độ H là nghiệm hệ:
Gọi A’ là điểm đối xứng với A qua H. Khi đó, H là trung điểm của AA’.
Suy ra:
Phương trình đường thẳng IA’: đi qua I(0; 1) và có vecto chỉ phương (2;4) ⇒ (2;-1) .
Phương trình IA’: 2( x- 0) - 1(y – 1) = 0 hay 2x – y + 1 = 0 chính là phương trình đường thẳng d’ đối xứng với d qua l.
Bài 3: Cho hai điểm A, B cùng phía với đường thẳng d. gọi A’, B’ lần lượt là hình chiếu của A, B trên đường thẳng d. Tìm vị trí điểm C trên d để chu vi tam giác ABC nhỏ nhất.
Lời giải:
Lấy A’’ đối xứng với A qua d.
Chu vi tam giác ABC = AB + AC + BC = AB + CA’’+ CB
Vì độ dài AB không đổi nên để chu vi tam giác ABC nhỏ nhất khi và chỉ khi CA” + CB nhỏ nhất.
Lại có: CA” + CB ≥ A”B
Do đó, để chu vi tam giác ABC nhỏ nhất khi và chỉ khi CA” + CB = A”B. Khi đó: B, C, A’’ thẳng hàng.
Bài 4: Có bao nhiêu phép đối xứng trục biến một hình chữ nhật thành chính nó?
Lời giải:
Hai đường thẳng đi qua tâm hình chữ nhật và vuông góc với hai cặp cạnh đối diện của nó.
Bài 5: Trong mặt phẳng Oxy cho đường thẳng d có phương trình x + y - 2 = 0. Phép đối xứng trục Oy biến d thành d’ có phương trình?
Lời giải:
Phép đối xứng trục Oy có:
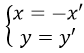
Thay vào phương trình d ta được -x' + y'- 2 = 0 hay - x + y - 2 = 0 ⇔ x - y + 2 = 0
Bài 6: Trong mặt phẳng Oxy cho parabol (P) có phương trình :y = 6x2 - 3x + 13. Phép đối xứng trục Ox biến (P) thành (P’) có phương trình:
Lời giải:
Phép đối xứng trục Ox có:
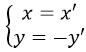
Thay vào phương trình (P) ta được :-y' = 6x'2 - 3x' + 13 hay y = -6x2 + 3x - 13
Bài 7: Trong mặt phẳng Oxy cho đường tròn (C) có phương trình: x2 + y2 - 4x + 5y + 1 = 0. Phép đối xứng trục Oy biến (C) thành (C’) có phương trình:
Lời giải:
Phép đối xứng qua trục Oy có :
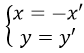
Thay vào phương trình (C) ta được x'2 + y'2 + 4x' + 5y' + 1 = 0 hay x2 + y2 + 4x + 5y + 1 = 0
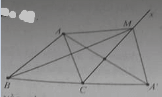
Bài 8: Trên tia phân giác ngoài Cx của góc C của tam giác ABC lấy điểm M không trùng với C. tìm mệnh đề đúng nhất:
Lời giải:
Lấy A’ đối xứng A qua Cx. Ta có:
MA + MB = MA’ + MB > BA’ = CB + CA’ = CB + CA
Nhận xét: Bất đẳng thức tam giác: Trong một tam giác bất kì luôn có tổng hai cạnh lớn hơn cạnh thứ ba (chú ý giả thiết : M không trùng với C).
Bài 9: Trong mặt phẳng Oxy cho parabol (P) có phương trình y = 4x2 - 7x + 3. Phép đối xứng trục Oy biến (P) thành (P’) có phương trình?
Lời giải:
Phép đối xứng trục Oy có:
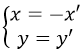
Thay vào phương trình (P) được y = 4x'2 + 7x' + 3 hay y = 4x2 + 7x + 3
Bài 10: Trong mặt phẳng Oxy cho A(1; -2) và B(3; 1). Tìm ảnh của A, B và đường thẳng AB qua phép đối xứng trục Ox.
Lời giải:
+ A’(x1; y1) đối xứng với A(1; -2) qua trục Ox
+ B’(x2; y2) đối xứng với B(3; 1) qua trục Ox
* Qua phép đối xứng trục Ox, biến điểm A và B lần lượt thành 2 điểm A’ và B’. Nên biến đường thẳng AB thành đường thẳng A’B’.
+ Đường thẳng A’B’ đi qua A’(1;2) và nhận vecto chỉ phương là (2,-3) nên vecto pháp tuyến là: (3; 2)
Phương trình đường thẳng A’B’ là:
3(x-1)+ 2( y-2) = 0 hay 3x+ 2y- 7=0
III. Bài tập vận dụng
Bài 1 Trong mặt phẳng Oxy cho đường thẳng d có phương trình 3x – y + 2 = 0. Viết phương trình của đường thẳng d’ là ảnh của d qua phép đối xứng trục Oy.
Bài 2 Trong các chữ cái sau, chữ nào là hình có trục đối xứng ?
Bài 3 Trong mặt phẳng Oxy cho hai điểm A(1;-2) và B(3;1). Tìm ảnh của A, B và đường thẳng AB qua phép đối xứng trục Ox.
Bài 4 Trong mặt phẳng Oxy cho đường thẳng d có phương trình 3x-y+2=0. Viết phương trình của đường thẳng d' là ảnh của d qua phép đối xứng trục Oy.
Bài 5 Trong các chữ cái sau, chữ nào là hình có trục đối xứng?

Bài 6 Trong mặt phẳng Oxy cho điểm . Điểm M (2;3) là ảnh của điểm nào trong bốn điểm sau qua phép đối xứng trục ?
Bài 7 Trong mặt phẳng Oxy cho A(1; -2) và B(3; 1). Tìm ảnh của A, B và đường thẳng AB qua phép đối xứng trục Ox.
Bài 8 Trong mặt phẳng cho hai đường thẳng a và b tạo với nhau góc 600. Có bao nhiêu phép đối xứng trục biến a thành b.
Bài 9 Trong mặt phẳng Oxy cho đường thẳng d có phương trình : x - 2y + 4 = 0. Phép đối xứng trục Ox biến d thành d’ có phương trình
Bài 10 Trong mặt phẳng Oxy cho điểm M(2;3). Điểm M là ảnh của điểm nào trong bốn điểm sau qua phép đối xứng trục Oy?
B. Lý thuyết Phép đối xứng trục
I. Định nghĩa.
- Cho đường thẳng d. Phép biến hình biến mỗi điểm M thuộc d thành chính nó, biến mỗi điểm M không thuộc d thành điểm M’ sao cho d là đường trung trực của đoạn MM’ được gọi là phép đối xứng qua đường thẳng d hay phép đối xứng trục d.
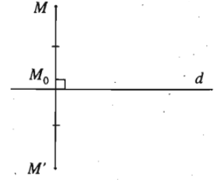
Đường thẳng d được gọi là trục của phép đối xứng hoặc đơn giản là trục đối xứng.
Phép đối xứng trục d thường được kí hiệu là Đd.
- Nếu hình ℋ ' là ảnh của hình ℋ qua phép đối xứng trục d thì ta còn nói ℋ đối xứng với ℋ ' qua d, hay ℋ và ℋ ' đối xứng với nhau qua d.
- Nhận xét:
1) Cho đường thẳng d. Với mỗi điểm M, gọi M0 là hình chiếu vuông góc của M
trên đường thẳng d. Khi đó: M’ = Đd(M)
2) M’ = Đd(M) M = Đd(M’).
II. Biểu thức tọa độ.
1) Chọn hệ trục tọa độ Oxy sao cho trục Ox trùng với đường thẳng d. Với mỗi điểm M = (x ; y), gọi M’ = Đd(M) = (x’ ; y’) thì , đây là biểu thức tọa độ của phép đối xứng qua trục Ox.
2) Chọn hệ trục tọa độ Oxy sao cho trục Oy trùng với đường thẳng d. Với mỗi điểm M = (x ; y), gọi M’ = Đd(M) = (x’; y’) thì , đây là biểu thức tọa độ của phép đối xứng qua trục Oy.
Ví dụ 1. Cho điểm M(2 ; 4). Tìm ảnh của điểm M qua phép đối xứng qua trục Ox và trục Oy.
Lời giải:
Gọi ĐOx(M) = A(x ; y) và ĐOy(M) = B(a; b)
Áp dụng biểu thức tọa độ của phép đối xứng trục Ox ta có:
Áp dụng biểu thức tọa độ của phép đối xứng trục Oy ta có:
III. Tính chất.
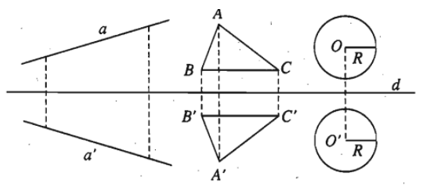
- Tính chất 1. Phép đối xứng trục bảo toàn khoảng cách giữa hai điểm bất kì.
- Tính chất 2. Phép đối xứng trục biến đường thẳng thành đường thẳng, biến đoạn thẳng thành đoạn thẳng bằng nó, biến tam giác thành tam giác bằng nó, biến đường tròn thành đường tròn có cùng bán kính.
Ví dụ 2. Trong mặt phẳng tọa độ Oxy, qua phép đối xứng trục Ox, đường tròn (C)
(x – 2)2 + (y – 3)2 = 36 biến thành đường tròn (C’). Tìm phương trình đường tròn (C’) ?
Lời giải:
Đường tròn (C) có tâm I(2 ; 3) và bán kính là R = 6.
Qua phép đối xứng trục Ox, biến đường tròn (C) thành đường tròn (C’), biến tâm I thành tâm I’(x’; y’) và bán kính R’ = R = 6.
Áp dụng biểu thức phép đối xứng trục Ox ta được I’(2; – 3)
Do đó, phương trình đường tròn (C’) là:
(x – 2)2 + (y + 3)2 = 36.
IV. Trục đối xứng của một hình
- Định nghĩa. Đường thẳng d được gọi là trục đối xứng của hình ℋ nếu phép đối xứng qua đường thẳng d biến ℋ thành chính nó.
Khi đó, ta nói ℋ là hình có trục đối xứng.
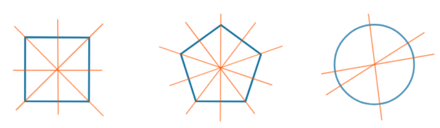
- Ví dụ 3. Các hình sau có trục đối xứng