Tailieumoi.vn xin giới thiệu Bài tập Toán 11 Chương 1 Bài 5: Phép quay. Bài viết gồm 50 bài tập với đầy đủ các mức độ và có hướng dẫn giải chi tiết sẽ giúp học sinh ôn luyện kiến thức và rèn luyện kĩ năng làm bài tập Toán 11. Ngoài ra, bài viết còn có phần tóm tắt nội dung chính lý thuyết Chương 1 Bài 5:Phép quay.Mời các bạn đón xem:
Bài tập Toán 11 Chương 1 Bài 5: Phép quay
A. Bài tập Phép quay
I. Bài tập trắc nghiệm
Bài 1: Trong mặt phẳng Oxy phép quay tâm K, góc 600 biến M(1;1) thành M’(-1;1). Tọa độ điểm K là:
A. (0;0)
B. (0;-)
C. (0;1-)
D. (;0)
Lời giải:
Đáp án: C
Tam giác đều KMM’ có cạnh MM’ = 2 nên đường cao bằng .
Suy ra OK = -1 ⇒ K(0; 1-)
Nhận xét. Phép quay có góc quay bằng ±600 thì tam giác tạo bởi tâm quay, điểm M và ảnh M’ của nó luôn tạo thành một tam giác đều.
Bài 2: Trong mặt phẳng Oxy phép quay Q(O; 600) biến đường thẳng d có phương trình x - 2y = 0 thành đường thẳng d’ có phương trình:
A. x + 2y = 0
B. 2x + y = 0
C. 2x - y = 0
D. x - y + 2 = 0
Lời giải:
Đáp án: B
Lấy M(2; 1) thuộc d, phép quay Q(O, 900) biến M(2; 1) thành M’(-1; 2). Tâm quay O(0; 0) thuộc d ⇒ d' đi qua O và M’ có phương trình 2x + y = 0.
Bài 3: trong mặt phẳng Oxy phép quay Q(O; 900) biến đường thẳng d có phương trình: 2x - y + 1 = 0 thành đường thẳng d’ có phương trình.
A. x + 2y - 1 = 0
B. 2x + y + 1 = 0
C. 2x - y + 1 = 0
D. x + 2y + 1 = 0
Lời giải:
Đáp án: D
Lấy A(0; 1) và B(-;0) thuộc d, phép quay Q(O, 900) biến A thành A’(-1; 0), biến B thành B’(0; -) phương trình d’ qua A’, B’ là x + 2y + 1 = 0.
Bài 4: Trong mặt phẳng Oxy cho đường tròn (C) có phương trình (x - 3)2 + y2 = 4. Phép quay tâm O(0;0) góc quay 900 biến (C) thành (C’) có phương trình:
A. x2 + y2 - 6x + 5 = 0
B. x2 + y2 - 6y + 6 = 0
C. x2 + y2 + 6x - 6 = 0
D. x2 + y2 - 6y + 5 = 0
Lời giải:
Đáp án: D
Phép quay tâm O(0; 0) góc quay 900 biến tâm I(3; 0) của (C) thành tâm I’(0; 3) của (C’), bán kính không thay đổi. phương trình (C’) là x2 + (y - 3)2 = 4 ⇒ x2 + y2 - 6y + 5 = 0
Bài 5: Cho một tam giác ABC tâm O. gọi A, E, F lần lượt là trung điểm các cạnh BC, CA, AB. Mệnh đề nào sau đây đúng?
A. Q(0; 1200)(∆ODC) = ∆OFA
B. Q(0; 1200)(∆AOF) = ∆BOD
C. Q(0; 1200)(∆AOB) = ∆AOC
D. Q(0; 600)(∆OFE) = ∆ODE
Lời giải:
Đáp án: B
D. Không có trên hình vẽ
Chọn đáp án B
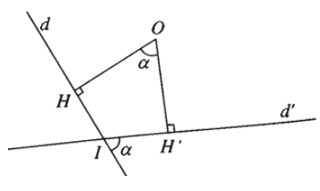
Bài 6: Dựng ra phía ngoài tam giác vuông cân ABC đỉnh A các tam giác đều ABD và ACE. Góc giữa hai đường thẳng BE và CD là:
A. 900
B. 600
C. 450
D. 300
Lời giải:
Đáp án: B
Xét phép quay tâm A góc quay 600 biến D thành B và biến C thành E, suy ra phép quay đó biến đường thẳng DC thành đường thẳng BE suy ra góc giữa DC và BE bằng góc quay 600. Chọn đáp án B.
Bài 7: Trong mặt phẳng tọa độ Oxy cho điểm M(1;0). Phép quay tâm O góc quay 450 biến M thành M’ có tọa độ
Lời giải:
Đáp án: D
Ta có OM’ = OM = 1; tứ giác OHM’K là hình vuông đường chéo bằng 1 suy ra cạnh bằng . Chọn đáp án D
Bài 8: Cho hình lục giác ABCDEF, tâm O. mệnh đề nào sau đây sai?
A. phép quay tâm O góc quay 600 biến tam giác BCD thành tam giác ABC.
B. phép quay tâm O góc quay 1200 biến tam giác OEC thành tam giác OCA
C. phép quay tâm O góc quay -600, biến tam giác AFD thành tam giác FEC.
D. phép quay tâm O góc quay -1200 biến tam giác BCD thành tam giác DEF.
Lời giải:
Đáp án: C
Phép quay tâm O góc quay -600 biến tam giác AFD thành tam giác ABE.
Bài 9: Cho ba điểm thẳng hàng A, B, C. dựng các tam giác đều ABD, BCE về cùng phía đối với đường thẳng AC. Gọi F, G lần lượt là trung điểm của các cạnh AE và DC. Tam giác BFG là:
A. tam giác thường
B. tam giác vuông đỉnh B
C. tam giác cân đỉnh B
D. tam giác đều
Lời giải:
Đáp án: D
(Hình 1) Xét phép quay tâm B góc quay -600 biến A thành D, biến E thành C suy ra phép quay này biến đoạn thẳng AE thành đoạn thẳng DC, suy ra nó biến trung điểm F của AE thành trung điểm G của DC, suy ra nó biến đoạn thẳng BF thành đoạn thẳng BG do đó BF = BG và góc FBG bằng 600. Vậy tam giác BFG là tam giác đều.
Bài 10: Cho hình thoi ABCD có góc A bằng 600.
a) Phép biến hình nào sau đây biến AB thành BC?
A. Đ0
B.
C. Q(D; 600)
D. Q(B; 1200)
b) Phép biến hình nào sau đây không biến A thành C?
A. ĐBD
B.
C. Q(B; 1200)
D. Q(B; 1200)
Lời giải:
Đáp án: a - C, b - D
(hình 2)
Chọn đáp án C
Phương án A. Đ0(AB) = CD
Phương án B. T2OC→(AB) = CB' với ACB'B là hình bình hành
Phương án D. Q(B,1200)(AB) = A' Bvới A' là điểm đối xứng của D và B.
Góc quay là -1200 (thuận chiều kim đồng hồ) thì A biến thành C
II. Bài tập tự luận có lời giải
Bài 1: Cho hình vuông ABCD tâm O. Gọi E, F lần lượt là trung điểm của các cạnh BC và CD?
a) phép biến hình nào biến thành
b) phép biến hình nào biến thành ?
Lời giải:
a) Xét từng điểm: Phép quay tâm O góc quay -900 biến B thành C, E thành F.
Q(A, 450)(B) = B' ≠ C và Q(A, 450)(E) = E' ≠ F(sai cả hai ảnh)
Q(A, -900)(B) = D và Q(A, 900)(E) = E' ≠ F(sai về chiều góc và ảnh của E)
Q(O, 900)(B) = A và Q(O, -900)(E) = F
b) Nhận xét. Khi luyện tập ta kiểm tra cả bốn phương án và trong mỗi phương án kiểm tra cả hai điểm B, D. còn trong khi kiểm tra, thi cử khi thấy ảnh của một điểm sai thì loại phương án đó; thấy ảnh của cả hai điểm đều đúng thì chọn phương án đó mà không cần kiểm tra các phương án còn lại.
Bài 2: Trong mặt phẳng Oxy, ảnh của điểm M (-6;1) qua phép quay Q(O; 900) là?
Lời giải:
Nhận xét. Cách làm các bài từ 5 đến 9: Vẽ hệ tọa độ Oxy, lấy điểm M, thực hiện phép quay. Chú ý chiều dương là ngược kim đồng hồ, chiều âm thuận chiều kim đồng hồ (hình 1)
Bài 3: Trong mặt phẳng Oxy qua phép quay Q(O; 900) thì M'(2; -3) là ảnh của điểm.
Lời giải:
(hình 2) vẽ ảnh của M’ qua phép quay Q(O, 900) là điểm M (- 3; -2)
Bài 4: Trong mặt phẳng Oxy cho điểm M(1;1). Điểm nào sau đây là ảnh của M qua phép quay tâm O, góc quay 450.
Lời giải:
Nhận xét. Hình vuông có cạnh bằng 1 thì đường chéo bằng .
Cho hình vuông ABCD tâm O.
a. Tìm ảnh của điểm C qua phép quay tâm A góc 90o.
b. Tìm ảnh của đường thẳng BC qua phép quay tâm O góc 90o
Lời giải:
a. Gọi C’ là điểm đối xứng với điểm C qua điểm D.
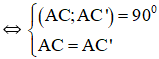
b) Ta có:
Bài 6 Trong mặt phẳng tọa độ Oxy cho điểm A(2; 0) và đường thẳng d có phương trình x + y – 2 = 0. Tìm ảnh của A và d qua phép quay tâm O góc 90o.
Lời giải:
* Ta có A(2; 0) thuộc tia Ox.
Gọi Q(O,90º) (A) = B thì B thuộc tia Oy và OA = OB nên B(0 ; 2).
* Gọi d’ là ảnh của d qua phép quay tâm O, góc quay 90º.
+ A(2 ; 0) ∈ (d)
⇒ B = Q(O,90º) (A) ∈ (d’)
+ B(0 ; 2) ∈ (d).
⇒ C = Q(O,90º) (B) ∈ (d’).
Dễ dàng nhận thấy C(-2; 0) (hình vẽ).
⇒ (d’) chính là đường thẳng BC.
Đường thẳng d’ đi qua B(0 ; 2) và C(-2; 0) nên có phương trình đoạn chắn là :
III. Bài tập vận dụng
Bài 1 Cho hình vuông ABCD tâm O
a) Tìm ảnh của điểm C qua phép quay tâm A góc .
b) Tìm ảnh của đường thẳng BC qua phép quay tâm O góc .
Bài 2 Trong mặt phẳng tọa độ Oxy cho điểm A(2,0) và đường thẳng d có phương trình . Tìm ảnh của A và d qua phép quay tâm O góc .
Bài 3 Cho ba điểm thẳng hàng A, B, C. dựng các tam giác đều ABD, BCE về cùng phía đối với đường thẳng AC. Gọi F, G lần lượt là trung điểm của các cạnh AE và DC. Tam giác BFG là?
Bài 4 Cho hình thoi ABCD có góc A bằng . Phép biến hình nào biến AB thành BC?
Bài 5 Trong mặt phẳng Oxy phép quay tâm K, góc 60 độ biến M(1;1) thành M’(-1;1). Tọa độ điểm K là?
Bài 6 Trong mặt phẳng Oxy phép quay Q(O; 600) biến đường thẳng d có phương trình x - 2y = 0 thành đường thẳng d’ có phương trình?
Bài 7 trong mặt phẳng Oxy phép quay Q(O; 900) biến đường thẳng d có phương trình: 2x - y + 1 = 0 thành đường thẳng d’ có phương trình.
Bài 8 Trong mặt phẳng Oxy cho đường tròn (C) có phương trình (x - 3)2 + y2 = 4. Phép quay tâm O(0;0) góc quay 900 biến (C) thành (C’) có phương trình?
Bài 9 Cho một tam giác ABC tâm O. gọi A, E, F lần lượt là trung điểm các cạnh BC, CA, AB. Mệnh đề nào sau đây đúng?
Bài 10 Dựng ra phía ngoài tam giác vuông cân ABC đỉnh A các tam giác đều ABD và ACE. Góc giữa hai đường thẳng BE và CD là?
B. Lý thuyết Phép quay
I. Định nghĩa.
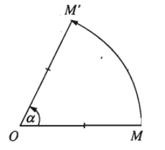
- Định nghĩa: Cho điểm O và góc lượng giác α. Phép biến hình biến O thành chính nó, biến mỗi điểm M khác O thành điểm M’ sao cho OM’ = OM và góc lượng giác (OM; OM’) bằng α được gọi là phép quay tâm O góc α.
- Điểm O được gọi là tâm quay, α được gọi là góc quay của phép quay đó.
Phép quay tâm O góc α được kí hiệu là Q(O, α).
- Nhận xét:
1) Chiều dương của phép quay là chiều dương của đường tròn lượng giác nghĩa là chiều ngược với chiều quay của kim đồng hồ.

2) Với k là số nguyên ta luôn có:
Phép quay là phép đồng nhất.
Phép quay là phép đối xứng tâm O.
II. Tính chất
- Tính chất 1. Phép quay bảo toàn khoảng cách giữa hai điểm bất kì.
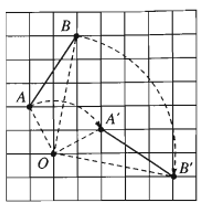
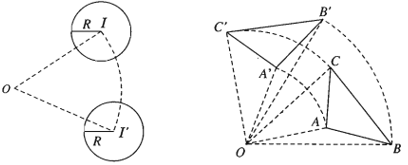
Phép quay tâm O, góc (OA, OA’) biến điểm A thành A’, B thành B’. Khi đó ta có A’B’ = AB.
- Tính chất 2. Phép quay biến đường thẳng thành đường thẳng, biến đoạn thẳng thành đoạn thẳng bằng nó, biến tam giác thành tam giác bằng nó, biến đường tròn thành đường tròn có cùng bán kính.
- Nhận xét: Phép quay góc α với , biến đường thẳng d thành đường thẳng d’ sao cho góc giữa d và d’ bằng α (nếu ), hoặc bằng (nếu