Tailieumoi.vn xin giới thiệu Trắc nghiệm Toán lớp 10 Bài 1: Quy tắc cộng và quy tắc nhân sách Chân trời sáng tạo. Bài viết gồm 20 câu hỏi trắc nghiệm với đầy đủ các mức độ và có hướng dẫn giải chi tiết sẽ giúp học sinh ôn luyện kiến thức và rèn luyện kĩ năng làm bài trắc nghiệm Toán 10.
Trắc nghiệm Toán 10 Bài 1: Quy tắc cộng và quy tắc nhân
I. Nhận biết
Câu 1. Lớp 10A có 23 học sinh nữ và 22 học sinh nam. Số cách chọn một bạn đại diện cả lớp tham gia cuộc thi điền kinh là:
A. 23;
B. 22;
C. 1;
D. 45.
Đáp án: D
Giải thích:
Công việc cử một học sinh có hai phương án thực hiện:
⦁ Phương án 1: Cử một học sinh nữ, có 23 cách thực hiện;
⦁ Phương án 2: Cử một học sinh nam, có 22 cách thực hiện.
Ta thấy mỗi cách thực hiện của phương án này không trùng với bất kì cách nào của phương án kia.
Do đó, theo quy tắc cộng, có 23 + 22 = 45 cách cử một học sinh đại diện cả lớp tham gia cuộc thi điền kinh.
Vậy ta chọn phương án D.
Câu 2. Có 3 kiểu mặt đồng hồ đeo tay (vuông, tròn, elip) và 4 kiểu dây (kim loại, da, vải, nhựa). Số cách chọn một chiếc đồng hồ gồm một mặt đồng hồ và một dây là:
A. 4;
B. 7;
C. 12;
D. 16.
Đáp án: C
Giải thích:
Công việc chọn một chiếc đồng hồ gồm hai công đoạn:
Công đoạn 1: Chọn một kiểu mặt đồng hồ, có 3 cách chọn.
Công đoạn 2: Ứng với mỗi cách chọn kiểu mặt đồng hồ, có 4 cách chọn kiểu dây.
Theo quy tắc nhân, có 3.4 = 12 cách chọn một chiếc đồng hồ.
Vậy ta chọn phương án C.
Câu 3. Giả sử một công việc có thể được thực hiện theo một trong hai phương án. Phương án thứ nhất có 10 cách thực hiện, phương án thứ hai có 5 cách thực hiện không trùng với bất kì cách nào của phương án thứ nhất. Khi đó, công việc có thể được thực hiện theo bao nhiêu cách?
A. 50 cách;
B. 15 cách;
C. 1 cách;
D. 125 cách.
Đáp án: B
Giải thích:
Công việc có hai phương án thực hiện:
⦁ Phương án thứ nhất có 10 cách thực hiện;
⦁ Phương án thứ hai có 5 cách thực hiện.
Ta thấy mỗi cách thực hiện của phương án này không trùng với bất kì cách nào của phương án kia. Do đó, theo quy tắc cộng, ta có 10 + 5 = 15 cách thực hiện công việc đã cho.
Vậy ta chọn phương án B.
Câu 4. Giả sử một công việc được chia thành hai công đoạn. Công đoạn thứ nhất có 2 cách thực hiện và ứng với mỗi cách đó có 6 cách thực hiện công đoạn thứ hai. Khi đó, công việc có thể thực hiện theo bao nhiêu cách?
A. 4 cách;
B. 8 cách;
C. 12 cách;
D. 40 cách.
Đáp án: C
Giải thích:
Công việc được chia thành hai công đoạn:
⦁ Công đoạn thứ nhất có 2 cách thực hiện;
⦁ Công đoạn thứ hai: ứng với mỗi cách thực hiện công đoạn thứ nhất, có 6 cách thực hiện.
Theo quy tắc nhân, ta có 2.6 = 12 cách thực hiện công việc đã cho.
Vậy ta chọn phương án C.
Câu 5. Giả sử một công việc có thể được thực hiện theo một trong ba phương án. Phương án A có 3 cách thực hiện, phương án B có 4 cách thực hiện, phương án C có 7 cách thực hiện (các cách thực hiện của cả ba phương án là khác nhau đôi một). Số cách thực hiện công việc đó là:
A. 14 cách;
B. 19 cách;
C. 84 cách;
D. 31 cách.
Đáp án: A
Giải thích:
Công việc có ba phương án thực hiện:
⦁ Phương án A có 3 cách thực hiện;
⦁ Phương án B có 4 cách thực hiện;
⦁ Phương án C có 7 cách thực hiện.
Ta thấy mỗi cách thực hiện của phương án này không trùng với bất kì cách nào của phương án kia. Do đó, theo quy tắc cộng, ta có 3 + 4 + 7 = 14 cách thực hiện công việc đã cho.
Vậy ta chọn phương án A.
Câu 6. Giả sử một công việc được chia thành ba công đoạn. Công đoạn A có 8 cách thực hiện; ứng với mỗi cách đó có 3 cách thực hiện công đoạn B; ứng với mỗi cách thực hiện công đoạn A và mỗi cách thực hiện công đoạn B có 6 cách thực hiện công đoạn C. Khi đó số cách thực hiện công việc đã cho là:
A. 17 cách;
B. 26 cách;
C. 30 cách;
D. 144 cách.
Đáp án: D
Giải thích:
Công việc được chia thành ba công đoạn:
⦁ Công đoạn A có 8 cách thực hiện;
⦁ Công đoạn B: ứng với mỗi cách thực hiện công đoạn A, có 3 cách thực hiện;
⦁ Công đoạn C: ứng với mỗi cách thực hiện công đoạn A và mỗi cách thực hiện công đoạn B, có 6 cách thực hiện.
Theo quy tắc nhân, ta có 8 . 3 . 6 = 144 cách thực hiện công việc đã cho.
Vậy ta chọn phương án D.
Câu 7. Cho kiểu gen AaBb. Giả sử quá trình giảm phân tạo giao tử bình thường và không xảy ra đột biến. Sơ đồ hình cây biểu thị sự hình thành giao tử được biểu diễn như hình bên.
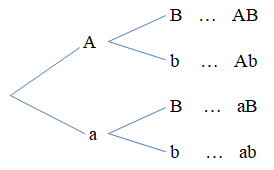
Từ sơ đồ cây, số loại giao tử của kiểu gen AaBb là:
A. 4;
B. 2;
C. 8;
D. 16.
Đáp án: A
Giải thích:
Từ sơ đồ cây, ta thấy có 4 kết quả có thể xảy ra.
Do đó số loại giao tử của kiểu gen AaBb là 4.
Vậy ta chọn phương án A.
II. Thông hiểu
Câu 1. Trong một tuần vào dịp nghỉ hè, bạn An dự định mỗi ngày đi thăm một người bạn trong 12 người bạn của mình. Hỏi bạn An có thể lập được bao nhiêu kế hoạch đi thăm bạn của mình (thăm một bạn không quá một lần)?
A. 3 991 680;
B. 479 001 600;
C. 35 831 808;
D. 5040.
Đáp án: A
Giải thích:
Theo đề, ta có mỗi tuần có 7 ngày, mỗi ngày bạn An đi thăm một người bạn (thăm một bạn không quá một lần).
⦁ Có 12 cách chọn một người bạn để đi thăm vào ngày thứ nhất.
⦁ Có 11 cách chọn một người bạn để đi thăm vào ngày thứ hai.
⦁ Có 10 cách chọn một người bạn để đi thăm vào ngày thứ ba.
⦁ Có 9 cách chọn một người bạn để đi thăm vào ngày thứ tư.
⦁ Có 8 cách chọn một người bạn để đi thăm vào ngày thứ năm.
⦁ Có 7 cách chọn một người bạn để đi thăm vào ngày thứ sáu.
⦁ Có 6 cách chọn một người bạn để đi thăm vào ngày thứ bảy.
Theo quy tắc nhân, ta có số cách lập kế hoạch của bạn An là:
12.11.10.9.8.7.6 = 3 991 680.
Vậy ta chọn phương án A.
Câu 2. Từ các chữ số 0; 1; 2; 3; 4; 5, có thể lập được bao nhiêu số lẻ gồm 4 chữ số khác nhau?
A. 154;
B. 145;
C. 144;
D. 155.
Đáp án: C
Giải thích:
Gọi là số cần tìm.
Vì số được lập là số lẻ nên vị trí d có 3 cách chọn một trong các số 1; 3; 5.
Ứng với mỗi cách chọn đó, có 4 cách chọn số ở vị trí a từ 4 chữ số khác 0 và khác số ở vị trí d đã cho.
Ứng với mỗi cách chọn đó, có 4 cách chọn số ở vị trí b từ 4 chữ số còn lại.
Ứng với mỗi cách chọn đó, có 3 cách chọn số ở vị trí c từ 3 chữ số còn lại.
Theo quy tắc nhân, ta có tất cả 3.4.4.3 = 144 cách lập một số thỏa mãn yêu cầu bài toán.
Vậy ta chọn phương án C.
Câu 3. Một người vào cửa hàng ăn, người đó chọn thực đơn gồm một món chính trong năm món chính, một loại quả tráng miệng trong năm loại quả tráng miệng và một loại nước uống trong ba loại nước uống. Số cách chọn thực đơn là:
A. 25;
B. 75;
C. 100;
D. 15.
Đáp án: B
Giải thích:
Việc chọn thực đơn gồm ba công đoạn:
Công đoạn 1: Chọn một món chính, có 5 cách chọn.
Công đoạn 2: Chọn một loại quả tráng miệng, có 5 cách chọn.
Công đoạn 3: chọn một loại nước uống, có 3 cách chọn.
Theo quy tắc nhân, ta có tất cả 5.5.3 = 75 cách chọn thực đơn.
Vậy ta chọn phương án B.
Câu 4. Trong một hộp chứa 6 quả cầu trắng được đánh số từ 1 đến 6 và ba quả cầu đen được đánh số 7; 8; 9. Có bao nhiêu cách chọn một trong các quả cầu ấy?
A. 27;
B. 9;
C. 6;
D. 3.
Đáp án: B
Giải thích:
Việc chọn một trong các quả cầu trong hộp có hai phương án thực hiện:
Phương án 1: Chọn một quả cầu màu trắng, có 6 cách chọn.
Phương án 2: Chọn một quả cầu màu đen, có 3 cách chọn.
Theo quy tắc cộng, ta có tất cả 6 + 3 = 9 cách chọn một quả cầu trong hộp.
Vậy ta chọn phương án B.
Câu 5. Từ các chữ số 1; 5; 6; 7; 9 có thể lập được bao nhiêu số tự nhiên có 4 chữ số?
A. 3 125;
B. 120;
C. 20;
D. 625.
Đáp án: D
Giải thích:
Gọi là số cần tìm.
Việc lập một số tự nhiên có 4 chữ số gồm 4 công đoạn:
Công đoạn 1: Chọn số ở vị trí a, có 5 cách chọn một chữ số từ các chữ số 1; 5; 6; 7; 9.
Công đoạn 2: Chọn số ở vị trí b, có 5 cách chọn một số từ các chữ số 1; 5; 6; 7; 9.
Công đoạn 3: Chọn số ở vị trí c, có 5 cách chọn một số từ các chữ số 1; 5; 6; 7; 9.
Công đoạn 4: Chọn số ở vị trí d, có 5 cách chọn một số từ các chữ số 1; 5; 6; 7; 9.
Theo quy tắc nhân, ta có tất cả 5.5.5.5= 54 = 625 cách lập một số tự nhiên có 4 chữ số.
Vậy ta chọn phương án D.
Câu 6. Trên bàn có 8 cây bút chì khác nhau, 6 cây bút bi khác nhau và 10 cuốn tập khác nhau. Một học sinh muốn chọn một đồ vật duy nhất (một cây bút chì hoặc một cây bút bi hoặc một cuốn tập) thì số cách chọn khác nhau là:
A. 24;
B. 480;
C. 48;
D. 60.
Đáp án: A
Giải thích:
Việc chọn một đồ vật duy nhất có ba phương án thực hiện:
Phương án 1: Chọn một cây bút chì, có 8 cách chọn.
Phương án 2: Chọn một cây bút bi, có 6 cách chọn.
Phương án 3: Chọn một cuốn tập, có 10 cách chọn.
Theo quy tắc cộng, ta có tất cả 8 + 6 + 10 = 24 cách chọn một đồ vật duy nhất.
Vậy ta chọn phương án A.
Câu 7. Hội đồng quản trị của công ty X gồm 10 người. Hỏi có bao nhiêu cách bầu ra ba người vào ba vị trí chủ tịch, phó chủ tịch và thư kí, biết khả năng mỗi người là như nhau.
A. 1 000;
B. 720;
C. 30;
D. 27.
Đáp án: B
Giải thích:
Việc bầu ra ba người vào ba vị trí chủ tịch, phó chủ tịch và thư kí gồm ba công đoạn:
Công đoạn 1: Bầu một người làm chủ tịch, có 10 cách chọn.
Công đoạn 2: Ứng với mỗi cách bầu một người làm chủ tịch, có 9 cách bầu một người làm phó chủ tịch.
Công đoạn 3: Ứng với mỗi cách bầu một người làm chủ tịch và bầu một người làm phó chủ tịch, có 8 cách bầu một người làm thư kí.
Theo quy tắc nhân, ta có tất cả 10.9.8 = 720 cách bầu ra ba người vào ba vị trí chủ tịch, phó chủ tịch và thư kí.
Vậy ta chọn phương án B.
Câu 8. Trong một cuộc thi tìm hiểu về đất nước Việt Nam, ban tổ chức công bố danh sách các đề tài bao gồm: 8 đề tài về lịch sử, 7 đề tài về thiên nhiên, 10 đề tài về con người và 6 đề tài về văn hóa. Mỗi thí sinh được quyền chọn một đề tài. Hỏi mỗi thí sinh có bao nhiêu cách chọn đề tài?
A. 20;
B. 3360;
C. 31;
D. 30.
Đáp án: C
Giải thích:
Việc chọn đề tài có 4 phương án thực hiện:
⦁ Phương án 1: Chọn đề tài về lịch sử, có 8 cách chọn;
⦁ Phương án 2: Chọn đề tài về thiên nhiên, có 7 cách chọn;
⦁ Phương án 3: Chọn đề tài về con người, có 10 cách chọn;
⦁ Phương án 4: Chọn đề tài về văn hóa, có 6 cách chọn.
Theo quy tắc cộng, ta có số cách chọn đề tài của mỗi thí sinh là: 8 + 7 + 10 + 6 = 31 cách chọn.
Vậy ta chọn phương án C.
III. Vận dụng
Câu 1. Từ các chữ số 1; 2; 3; 4; 5; 6, có thể lập được bao nhiêu số tự nhiên bé hơn 100?
A. 36;
B. 62;
C. 54;
D. 42.
Đáp án: D
Giải thích:
Các số bé hơn 100 là các số có một chữ số và các số có hai chữ số.
Việc lập các số bé hơn 100 từ các chữ số 1; 2; 3; 4; 5; 6 có hai phương án thực hiện:
Phương án 1: Lập số có một chữ số từ các chữ số 1; 2; 3; 4; 5; 6.
Khi đó có thể lập được 6 số.
Phương án 2: Lập số có hai chữ số từ các chữ số 1; 2; 3; 4; 5; 6.
Gọi là số cần tìm.
Chọn số ở vị trí a, có 6 cách chọn.
Chọn số ở vị trí b, có 6 cách chọn.
Theo quy tắc nhân, ta có 6.6 = 36 cách lập một số có hai chữ số từ các chữ số 1; 2; 3; 4; 5; 6.
Vậy theo quy tắc cộng, ta có tất cả 6 + 36 = 42 số tự nhiên bé hơn 100.
Do đó ta chọn phương án D.
Câu 2. Một mạng đường giao thông nối các tỉnh A, B, C, D, E, F và G như hình vẽ, trong đó chữ số được viết trên mỗi cạnh là số con đường có thể đi từ tỉnh này đến tỉnh kia, chẳng hạn chữ số 2 viết trên cạnh AB có nghĩa là có 2 con đường nối A và B,...
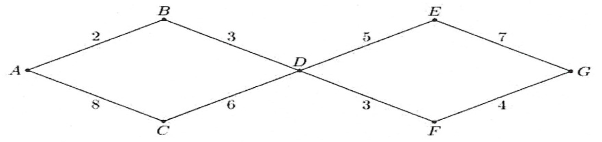
Số con đường từ A đến G là:
A. 101;
B. 2 538;
C. 38;
D. 1 462.
Đáp án: D
Giải thích:
Ta thấy để đi từ A đến G, ta bắt buộc phải đi qua D.
Bước 1: Đi từ A đến D.
• Phương án 1: Đi từ A, qua B, đến D thì có 2.3 = 6 con đường.
• Phương án 2: Đi từ A, qua C, đến D thì có 8.6 = 48 con đường.
Theo quy tắc cộng, ta có số cách đi từ A đến D là 6 + 48 = 54 con đường.
Bước 2: Đi từ D đến G.
• Phương án 1: Đi từ D, qua E, đến G thì có 5.7 = 35 con đường.
• Phương án 2: Đi từ D, qua F, đến G thì có 3.4 = 12 con đường.
Theo quy tắc cộng, ta có số cách đi từ D đến G là 35 + 12 = 47 con đường.
Vậy theo quy tắc nhân, ta có số cách đi từ A đến G là 54.47 = 2 538 con đường.
Do đó ta chọn phương án B.
Câu 3. Biển số xe máy của tỉnh A (không gồm kí hiệu địa phương đăng kí xe và seri đăng kí) thì có 5 kí tự, mỗi kí tự là một chữ số thuộc tập hợp {0; 1; 2; 3; 4; 5; 6; 7; 8; 9} và không có biển số xe 000.01. Hỏi nếu hai kí tự đầu tiên đều không nhỏ hơn 7 thì tỉnh A có thể làm được nhiều nhất bao nhiêu biển số xe máy?
A. 4 000;
B. 34;
C. 36;
D. 9 000.
Đáp án: A
Giải thích:
Việc chọn một biển số xe gồm 4 công đoạn:
Công đoạn 1: chọn kí tự ở vị trí đầu tiên, có 2 cách chọn một chữ số không nhỏ hơn 7 là 8; 9.
Công đoạn 2: chọn kí tự ở vị trí thứ hai, có 2 cách chọn một chữ số không nhỏ hơn 7 là 8; 9.
Công đoạn 3: chọn kí tự ở vị trí thứ ba, có 10 cách chọn một chữ số thuộc tập hợp {0; 1; 2; 3; 4; 5; 6; 7; 8; 9}.
Công đoạn 4: chọn kí tự ở vị trí thứ tư, có 10 cách chọn một chữ số thuộc tập hợp {0; 1; 2; 3; 4; 5; 6; 7; 8; 9}.
Công đoạn 5: chọn kí tự ở vị trí thứ năm, có 10 cách chọn một chữ số thuộc tập hợp {0; 1; 2; 3; 4; 5; 6; 7; 8; 9}.
Theo quy tắc nhân, ta có tất cả 2.2.10.10.10 = 4 000 cách chọn một biển số xe.
Vậy ta chọn phương án A.
Câu 4. Số 253 125 000 có bao nhiêu ước số tự nhiên?
A. 160;
B. 240;
C. 180;
D. 120.
Đáp án: C
Giải thích:
Ta có 253 125 000 = 23.34.58.
Do đó mỗi ước số tự nhiên của số 253 125 000 đều có dạng 2m.3n.5p, trong đó 0 ≤ m ≤ 3, 0 ≤ n ≤ 4, 0 ≤ p ≤ 8 và m, n, p ∈ ℕ.
Khi đó:
⦁ m có 4 cách chọn;
⦁ n có 5 cách chọn;
⦁ p có 9 cách chọn.
Theo quy tắc nhân, ta có tất cả 4.5.9 = 180 ước số tự nhiên.
Vậy ta chọn phương án C.
Câu 5. Cho tập hợp A = {0; 1; 2; 3; 4; 5; 6; 7}. Hỏi từ tập A có thể lập được bao nhiêu số tự nhiên gồm 5 chữ số đôi một khác nhau sao cho một trong 3 chữ số đầu tiên có chữ số 1?
A. 2 802;
B. 65;
C. 2 520;
D. 2 280.
Đáp án: D
Giải thích:
Gọi là số cần tìm.
Trường hợp 1: a = 1.
Khi đó b có 7 cách chọn, c có 6 cách chọn, d có 5 cách chọn và e có 4 cách chọn.
Do đó theo quy tắc nhân, ta có 7.6.5.4 = 840 số được lập.
Trường hợp 2: b = 1 hoặc c = 1 thì có 2 cách.
Khi đó a có 6 cách chọn (vì a ≠ 0 và a ≠ 1).
Ba vị trí còn lại lần lượt có 6, 5, 4 cách chọn.
Do đó theo quy tắc nhân, ta có 2.6.6.5.4 = 1 440 số được lập.
Vậy theo quy tắc cộng, ta có tất cả 840 + 1 440 = 2 280 số được lập.
Do đó ta chọn phương án D.
Xem thêm các bài trắc nghiệm Toán 10 Chân trời sáng tạo hay, chi tiết khác:
Trắc nghiệm Bài 1. Quy tắc cộng và quy tắc nhân
Trắc nghiệm Bài 2. Hoán vị, chỉnh hợp và tổ hợp