Tailieumoi.vn xin giới thiệu Trắc nghiệm Toán lớp 7 Bài 13: Hai tam giác bằng nhau. Trường hợp bằng nhau thứ nhất của tam giác sách Kết nối tri thức. Bài viết gồm 20 câu hỏi trắc nghiệm với đầy đủ các mức độ và có hướng dẫn giải chi tiết sẽ giúp học sinh ôn luyện kiến thức và rèn luyện kĩ năng làm bài trắc nghiệm Toán 7. Ngoài ra, bài viết còn có phần tóm tắt nội dung chính lý thuyết Bài 13: Hai tam giác bằng nhau. Trường hợp bằng nhau thứ nhất của tam giác. Mời các bạn đón xem:
Trắc nghiệm Toán 7 Bài 13: Hai tam giác bằng nhau. Trường hợp bằng nhau thứ nhất của tam giác
I. Nhận biết
Câu 1. Cho ∆DEF và tam giác tạo bởi ba đỉnh M, N, P là hai tam giác bằng nhau. Biết rằng mỗi tam giác không có hai cạnh nào bằng nhau và không có hai góc nào bằng nhau. Biết và FD = PN. Cách kí hiệu nào sau đây đúng?
A. ∆DFE = ∆PMN;
B. ∆DEF = ∆MNP;
C. ∆DEF = ∆PMN;
D. ∆DEF = ∆MPN.
Hướng dẫn giải
Đáp án: C
Giải thích:
Ta có (giả thiết)
Do đó D và P là hai đỉnh tương ứng.
Mà FD = PN.
Suy ra F và N là hai đỉnh tương ứng.
Từ đó ta có E và M là hai đỉnh tương ứng.
Vì vậy ta kí hiệu là: ∆DEF = ∆PMN.
Do đó ta chọn phương án C.
Câu 2. Cho ∆GHK và tam giác tạo bởi ba đỉnh P, Q, R là hai tam giác bằng nhau. Biết rằng mỗi tam giác không có hai cạnh nào bằng nhau và không có hai góc nào bằng nhau. Biết và . Cách kí hiệu nào sau đây đúng?
A. ∆GHK = ∆QPR;
B. ∆HKG = ∆QPR;
C. ∆GHK = ∆PQR;
D. ∆GHK = ∆RQP.
Hướng dẫn giải
Đáp án: A
Giải thích:
Ta có (giả thiết)
Suy ra H và P là hai đỉnh tương ứng (1)
Lại có (giả thiết)
Suy ra K và R là hai đỉnh tương ứng (2)
Từ (1), (2), ta suy ra G và Q là hai đỉnh tương ứng còn lại.
Vì vậy ta kí hiệu là: ∆GHK = ∆QPR.
Do đó ta chọn phương án A.
Câu 3. Cho ∆ABC và tam giác tạo bởi ba đỉnh H, I, K bằng nhau. Biết rằng mỗi tam giác không có hai cạnh nào bằng nhau và không có hai góc nào bằng nhau. Biết AC = IK, BC = HI. Cách kí hiệu nào sau đây đúng?
A. ∆ABC = ∆KHI;
B. ∆ABC = ∆IKH;
C. ∆ABC = ∆HKI;
D. ∆ABC = ∆KIH.
Hướng dẫn giải
Đáp án: A
Giải thích:
Ta có AC = IK và BC = HI (giả thiết)
Do đó C và I là hai đỉnh tương ứng.
Suy ra A và K; B và H là hai cặp đỉnh tương ứng còn lại.
Vì vậy ta kí hiệu là: ∆ABC = ∆KHI.
Vậy ta chọn phương án A.
Câu 4. Cho hình vẽ bên.
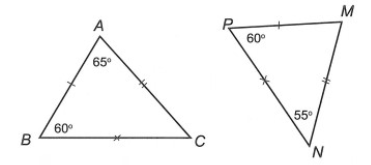
Kết luận nào sau đây đúng?
A. ∆ABC = ∆MNP;
B. ∆ABC = ∆PMN;
C. ∆ABC = ∆MPN;
D. Hai tam giác đã cho không bằng nhau.
Hướng dẫn giải
Đáp án: C
Giải thích:
Câu 5. Cho ∆ABC = ∆MNP. Khẳng định nào sau đây sai?
A. AB = MN;
B. ;
C. MP = AC;
D. .
Hướng dẫn giải
Đáp án: B
Giải thích:
Ta có ∆ABC = ∆MNP (giả thiết)
Suy ra:
⦁ AB = MN; AC = MP và BC = NP (các cặp cạnh bằng nhau);
⦁ và (các cặp góc bằng nhau).
Vì AB = MN nên phương án A đúng.
Vì MP = AC nên phương án C đúng.
Vì nên phương án D đúng.
Vì vậy phương án B sai.
Do đó ta chọn phương án B.
II. Thông hiểu
Câu 1. Cho hình bên.
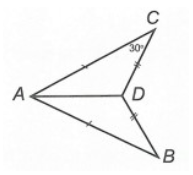
Số đo của bằng:
A. 30°;
B. 45°;
C. 60°;
D. 85°.
Hướng dẫn giải
Đáp án: A
Giải thích:
Xét ∆ADB và ∆ADC, có:
AD là cạnh chung.
AB = AC (giả thiết)
DB = DC (giả thiết)
Do đó ∆ADB = ∆ADC (c.c.c)
Suy ra (cặp góc tương ứng)
Vậy ta chọn phương án A.
Câu 2. Cho ∆ABC có AB = AC. Gọi D, E là hai điểm thuộc cạnh BC sao cho BD = DE = EC. Biết AD = AE. Khẳng định nào sau đây đúng nhất?
A. BE = CD;
B. ∆ABE = ∆ACD;
C. ;
D. Cả A, B, C đều đúng.
Hướng dẫn giải
Đáp án: D
Giải thích:
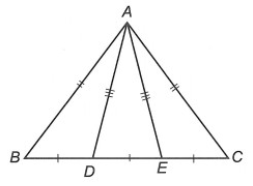
⦁ Ta có BD = EC (giả thiết)
Suy ra BD + DE = DE + EC.
Khi đó BE = CD.
Vì vậy phương án A đúng.
⦁ Xét ∆ABE và ∆ACD, có:
AB = AC (giả thiết)
AD = AE (giả thiết)
BE = CD (chứng minh trên)
Do đó ∆ABE = ∆ACD (c.c.c)
Vì vậy phương án B đúng.
⦁ Ta có ∆ABE = ∆ACD (chứng minh trên)
Suy ra (cặp góc tương ứng)
Do đó phương án C đúng.
Vậy ta chọn phương án D.
Câu 3. Quan sát hình bên.
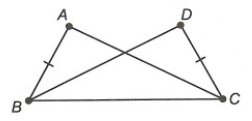
Để ∆ABC = ∆DCB theo trường hợp cạnh – cạnh – cạnh thì cần thêm điều kiện:
A. AC = BC;
B. AC = DB;
C. BD = BC;
D. AB = AD.
Hướng dẫn giải
Đáp án: B
Giải thích:
Xét ∆ABC và ∆DCB, có:
BC là cạnh chung.
AB = DC (giả thiết)
Do đó để ∆ABC = ∆DCB theo trường hợp cạnh – cạnh – cạnh thì cần thêm điều kiện về cạnh là AC = DB.
Vậy ta chọn phương án B.
Câu 4. Cho ∆ABC và ∆DEF có AB = DF, AC = DE và BC = FE. Khẳng định nào sau đây đúng?
A. ∆ABC = ∆DFE;
B. ∆ABC = ∆DEF;
C. ∆ABC = ∆EFD;
D. ∆ABC = ∆EDF.
Hướng dẫn giải
Đáp án: A
Giải thích:
Xét ∆ABC và ∆DFE, có:
AB = DF (giả thiết)
AC = DE (giả thiết)
BC = FE (giả thiết)
Do đó ∆ABC = ∆DFE (c.c.c)
Vậy ta chọn phương án A.
Câu 5. Cho ∆ABC và ∆MNP bằng nhau. Biết số đo các góc như hình vẽ sau:
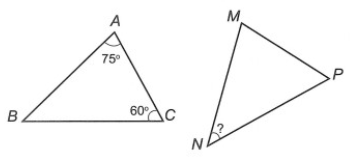
Số đo của bằng:
A. 60°;
B. 45°;
C. 30°;
D. 75°.
Hướng dẫn giải
Đáp án: B
Giải thích:
∆ABC có: (định lí tổng ba góc trong một tam giác)
Suy ra .
Ta có ∆ABC = ∆MNP (giả thiết)
Suy ra (cặp góc tương ứng)
Vậy ta chọn phương án B.
Câu 6. Cho hình vẽ bên.
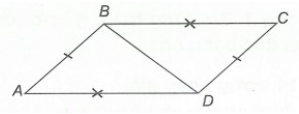
Kết luận nào sau đây đúng?
A. ∆ABD = ∆BCD;
B. ∆BAD = ∆CDB;
C. ∆ABD = ∆CBD;
D. ∆ABD = ∆CDB.
Hướng dẫn giải
Đáp án: D
Giải thích:
Xét ∆ABD và ∆CDB, có:
BD là cạnh chung.
AB = CD (giả thiết)
AD = CB (giả thiết)
Do đó ∆ABD = ∆CDB (c.c.c)
Vậy ta chọn phương án D.
Câu 7. Cho ∆ABC có M là trung điểm BC, N là một điểm nằm bên trong ∆ABC sao cho NB = NC. Kết luận nào sau đây đúng?
A. ∆NMB = ∆CNM;
B. ∆BMC = ∆NMC;
C. ∆NMB = ∆NMC;
D. ∆NMB = ∆CMN.
Hướng dẫn giải
Đáp án: C
Giải thích:
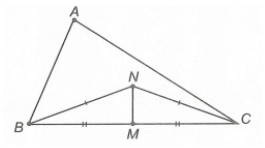
Xét ∆NMB và ∆NMC, có:
NB = NC (giả thiết)
MB = MC (M là trung điểm BC)
NM là cạnh chung.
Do đó ∆NMB = ∆NMC (c.c.c)
Vậy ta chọn phương án C.
III. Vận dụng
Câu 1. Cho ∆ABC = ∆IHK, biết AB = 5 cm, HK = 9 cm và IK = 12 cm. Chu vi ∆ABC bằng:
A. 13 cm;
B. 52 cm;
C. 26 cm;
D. 16 cm.
Hướng dẫn giải
Đáp án: A
Giải thích:
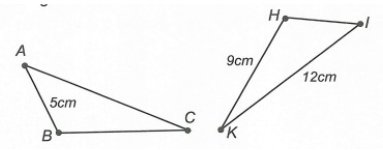
Ta có ∆ABC = ∆IHK (giả thiết)
Suy ra AB = HI = 5 cm; BC = HK = 9 cm; AC = IK = 12 cm.
Vậy chu vi của ∆ABC là: AB + AC + BC = 5 + 12 + 9 = 26 (cm).
Do đó ta chọn phương án C.
Câu 2. Cho bốn điểm A, B, C, D thuộc đường tròn (O) sao cho AB = CD. Khẳng định nào sau đây sai?
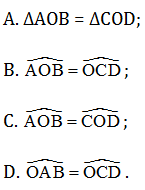
Hướng dẫn giải
Đáp án: B
Giải thích:
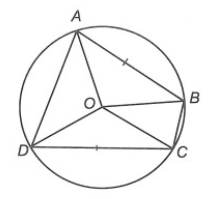
⦁ Xét ∆AOB và ∆COD, có:
OA = OC (= R)
OB = OD (= R)
AB = CD (giả thiết)
Do đó ∆AOB = ∆COD (c.c.c)
Vì vậy phương án A đúng.
⦁ Ta có ∆AOB = ∆COD (chứng minh trên)
Suy ra và (các cặp góc tương ứng)
Vì vậy phương án B sai, phương án C, D đúng.
Vậy ta chọn phương án B.
Câu 3. Cho là góc nhọn. Trên tia Ox và Oy, lần lượt lấy hai điểm A và B sao cho OA = OB. Gọi M là trung điểm của đoạn thẳng AB. Kết luận nào sau đây đúng nhất?
A. ;
B. OM ⊥ AB;
C. OM là tia phân giác của ;
D. Cả B, C đều đúng.
Hướng dẫn giải
Đáp án: C
Giải thích:
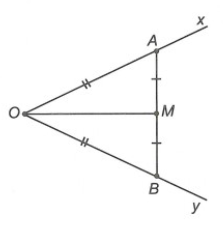
Xét ∆OAM và ∆OBM, có:
OM là cạnh chung.
OA = OB (giả thiết)
MA = MB (M là trung điểm của đoạn thẳng AB)
Do đó ∆OAM = ∆OBM (c.c.c)
Suy ra và (các cặp góc tương ứng)
⦁ Vì nên OM là tia phân giác của .
Do đó phương án C đúng.
⦁ Vì nên phương án A sai.
⦁ Ta có (hai góc kề bù)
Suy ra .
Do đó OM ⊥ AB.
Vì vậy phương án B đúng.
Vậy ta chọn phương án D.
Xem thêm các bài trắc nghiệm Toán 7 Kết nối tri thức hay, chi tiết khác:
Trắc nghiệm Tổng các góc trong một tam giác
Trắc nghiệm Hai tam giác bằng nhau. Trường hợp bằng nhau thứ nhất của tam giác
Trắc nghiệm Trường hợp bằng nhau thứ hai và thứ ba của tam giác
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
