Tailieumoi.vn xin giới thiệu chuyên đề Phép vị tự thuộc chương trình Toán 11. Chuyên đề gồm 6 trang với đầy đủ lý thuyết, phương pháp giải các dạng bài tập và trên 200 bài tập có lời giải chi tiết từ cơ bản đến nâng cao giúp học sinh ôn luyện kiến thức, nâng cao kĩ năng làm bài tập môn Toán 11.
Chuyên đề Phép vị tự
Phần 1: Tìm ảnh của một điểm qua phép vị tự cực hay
Ví dụ 1: Trong hệ trục tọa độ Oxy, tìm ảnh của các điểm sau qua phép vị tự tâm O, tỉ số k, biết:
Hướng dẫn giải:
Ví dụ 2: Trong hệ trục tọa độ Oxy, tìm tọa độ của điểm A sao cho B là ảnh của A qua phép vị tự tâm O, tỉ số k, biết:
Hướng dẫn giải:
Ví dụ 3: Tìm tỉ số k, biết V(O,k)(A) = A':
a) A(-2; 4), A’(1; -2)
b) A(4; 5), A’(-8; -10)
Hướng dẫn giải:
Phần 2: Tìm ảnh của một đường thẳng qua phép vị tự cực hay
● Cách 1. Sử dụng tính chất: Phép vị tự biến một đường thẳng thành đường thẳng song song hoặc trùng với nói.
● Cách 2. Dùng biểu thức tọa độ của phép vị tự.
Ví dụ 1: Trong mặt phẳng Oxy, cho đường thẳng d có phương trình 5x + 2y-7 = 0. Hãy viết phương trình của đường thẳng d' là ảnh của d qua phép vị tự tâm O tỉ số k = -2.
Hướng dẫn giải:
Cách 1: Lấy M(x;y) ∈ d ⇒ 5x + 2y - 7 = 0 (*).
Gọi M'(x';y') = V(O,-2)(M).
Theo biểu thức tọa độ ta có:
Thay vào (*) ta được 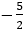
Vậy d': 5x + 2y + 14 = 0.
Cách 2: Do d' song song hoặc trùng với d nên phương trình có dạng : 5x + 2y+c = 0.
Lấy M(1;1) thuộc d. Gọi M'(x';y') = V(O,-2)(M) ta có
Thay vào (*)ta được c = 14.
Vậy d': 5x + 2y + 14 = 0.
Ví dụ 2: Tìm ảnh của các đt d sau qua phép vị tự tâm O, tỉ số k, biết:
a) d: 4x – 3y + 1 = 0, k = -3
b) d: x – 4y + 2 = 0, k = 1/2
Hướng dẫn giải:
a)
* Cách 1: Gọi V(O,-3)(d) = d' ⇒ d’ // d nên PT đt d’ có dạng: 4x – 3y + C = 0
Chọn A(2; 3) ∈ d V(O,-3)(A) = A' (-6; -9) ∈ d’. Khi đó: -24 + 27 + C = 0 ⇔ C = -3
Vậy: PT đt d’ là: 4x – 2y – 3 = 0
* Cách 2: Chọn A(2; 3) ∈ d V(O,-3)(A) = A' (-6; -9) ∈ d’ và B(-1; -1) ∈ d V(O,-3)(B) = B' (3; 3) ∈ d’
PT đt d’ đi qua 2 điểm A’, B’ là:
b)
* Cách 1: Gọi 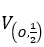
Chọn A(-2; 0) ∈ d 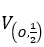
Vậy: PT đt d’ là: x – 4y + 1 = 0
* Cách 2: Chọn A(-2; 0) ∈ d 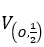
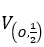
PT đt d’ đi qua 2 điểm A’, B’ là:
Ví dụ 3: Trong mặt phẳng tọa độ Oxy, cho đường thẳng (d) có phương trình 2x + 3y - 1 = 0 và điểm I(-1;3), phép vị tự tâm I tỉ số k = -3 biến đường thẳng (d) thành đường thẳng (d'). Viết phương trình đường thẳng (d')
Hướng dẫn giải:
Chọn B
Đường thẳng (d') có dạng: 2x + 3y + m = 0.
Lấy A(-1;1) ∈ (d), gọi A'(x;y) là ảnh của A qua
Phần 3:Tìm ảnh của một đường tròn qua phép vị tự cực hay
Cách 1. Sử dụng quỹ tích: Với mọi điểm M(x;y) thuộc hình (C), V(O,k)(M) = M'(x';y') thì M'thuộc ảnh (C') của hình (C).
Cách 2. áp dụng tính chất phép vị tự biến đường tròn bán kính R thành đường tròn bán kính |k|R
Ví dụ 1: Trong mặt phẳng Oxy, cho đường tròn (C): (x - 1)2 + (y - 1)2 = 4. Tìm ảnh của đường tròn (C) qua phép vị tự tâm I(-1;2) tỉ số k = 3
Hướng dẫn giải:
Đường tròn (C) có tâm J(1;1), bán kính R = 2.
⇒ J'(7;-2).
Gọi (C') là ảnh của (C) qua phép vị tự V(I;3) thì(C') có tâm J'(7;-2), bán kính R' = 3R = 6.
Vậy (C'): (x - 7)2 + (y + 2)2 = 36.
Ví dụ 2: Tìm ảnh của các đường tròn (C) sau qua phép vị tự tâm O, tỉ số k, biết:
a) (C): (x – 2)2 + (y + 4)2 = 1, k = -1/2
b) (C): x2 + y2 – 6x + 4y – 3 = 0, k = 4
Hướng dẫn giải:
a)
b)
Gọi V(O,4)(C) = (C'). Từ (C), ta có: tâm I(3; -2) và bán kính R = 4
Khi đó: V(O,4)(I) = I'(12; -8) và bán kính R’ = |4|R = 16.
Vậy: (C’): (x – 12)2 + (y + 8)2 = 256
Ví dụ 3: Cho hai đường tròn (C): (x - 2)2 + (y - 1)2 = 4 và (C'): (x - 8)2 + (y - 4)2 =16. Tìm tâm vị tự của hai đường tròn.
Hướng dẫn giải:
Đường tròn (C) có tâm I(1;2),bán kính R = 2; đường tròn (C') có tâm I'(8;4), bán kính R' = 4. Do I ≠ I' và R ≠ R' nên có hai phép vị tự V(J;2) và V(J';-2) biến (C) thành (C'). Gọi J(x;y)
Với k = 2 khi đó
⇒ J(-4;-2).
Tương tự với k = -2, tính được J'(4;2).





