Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu bài tập Phép vị tự và phép đồng dạng Toán lớp 11, tài liệu bao gồm 5 trang, tuyển chọn 10 bài tập Phép vị tự và phép đồng dạng đầy đủ lý thuyết, phương pháp giải, giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kì thi môn Toán sắp tới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Tài liệu Lý thuyết, bài tập về Phép vị tự và phép đồng dạng gồm các nội dung sau:

A. LÝ THUYẾT CƠ BẢN

I. Phép vị tự

1. Định nghĩa

Cho điểm $O$ và số $k\ne 0$. Phép biến hình biến mỗi điểm $M$ thành điểm $M^{\prime }$ sao cho $\overrightarrow{O{M}^{\prime }}=k$ $\overrightarrow{OM}$, được gọi là phép vị tự tâm $O$, tỉ số $k$

Phép vị tự tâm $O$, tỉ số $k$ và thường được kí hiệu là $V_{(O,k)}$

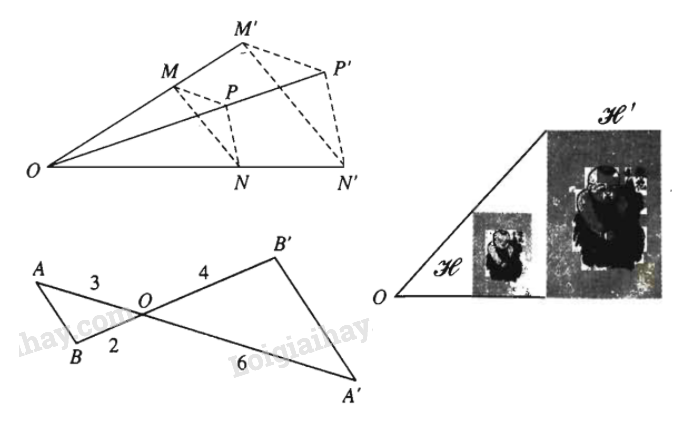
 Nhận xét

- Phép vị tự biến tâm vị tự thành chính nó

- Khi $k=1$, phép vị tự là phép đồng nhất

- Khi $k=-1$, phép vị tự là phép đối xứng qua tâm vị tự

- $M^{\prime }$ = ${V_{(O,k)}}^{}(M)$ $\iff M=$ $V_{(O,\frac{1}{k})}(M^{\prime })$

2. Tính chất

- Nếu phép vị tự tâm $O$ tỉ số $k$ biến hai điểm $M,N$ tùy ý theo thứ tự thành $M^{\prime },N^{\prime }$ thì $\overrightarrow{M^{\prime }{N}^{\prime }}$ =$k\overrightarrow{MN}$ và $M^{\prime }{N}^{\prime }=|k|MN$

- Phép vị tự tỉ số $k$ có các tính chất:

a) Biến ba điểm thẳng hàng thành ba điểm thẳng hàng và bảo toàn thứ tự giữa các điểm ấy

b) Biến đường thẳng thành đường thẳng song song hoặc trùng với nó, biến tia thành tia, biến đoạn thẳng có độ dài bằng $a$ thành đoạn thẳng có độ dài bằng $|k|a$

c) Biến tam giác thành tam giác đồng dạng với tỉ số đồng dạng là $|k|$, biến góc thành góc bằng nó.

d) Biến đường tròn bán kính $R$ thành đường tròn bán kính $|k|R$.

3. Tâm vị tự của hai đường tròn

Định lí: Với hai đường tròn bất kì, luôn có một phép vị tự biến đường tròn này thành đường tròn kia.

Cách tìm tâm vi tự:

+ TH1: hai tâm trùng nhau

+ TH2: hai tâm khác nhau

+ Th3: hai tâm khác nhau, bán kính bằng nhau

4. Biểu thức tọa độ của phép vị tự

Cho điểm $M\left(x_0;y_0\right)$.

Phép vị tự tâm $O\left(a;b\right)$, tỉ số $k$ biến điểm $M$ thành $M^{\prime }$ có tọa độ $\left(x^{\prime };y^{\prime }\right)$ thỏa mãn:

$\{\begin{array}{l}{x}^{\prime }-a=k\left(x_0-a\right)\\ y^{\prime }-b=k\left(y_0-b\right)\end{array}$

II. Phép đồng dạng

1. Định nghĩa

Phép biến hình $f$ được gọi là phép đồng dạng tỉ số $k$, $(k>0)$, nếu với hai điểm $M,N$ bất kì và ảnh $M^{\prime },N^{\prime }$ tương ứng của chúng, ta luôn có $M^{\prime }{N}^{\prime }=kMN$

2. Nhận xét

a) Phép dời hình là phép đồng dạng tỉ số $1$

b) Phép vị tự tỉ số $k$ là phép đồng dạng tỉ số $|k|$

c) Nếu thực hiện liên tiếp phép đồng dạng tỉ số $k$ và phép đồng dạng tỉ số $p$ ta được phép đồng dạng tỉ số $pk$

d) Phép đồng dạng tỉ số $k$ là hợp thành của một phép dời hình và một phép vị tự tỉ số $k$ hoặc $-k$. Nó cũng là hợp thành của một phép vị tự tỉ số $k$ hoặc $-k$ và một phép dời hình

3. Tính chất

Phép đồng dạng tỉ số $k$ có các tính chất:

a) Biến ba điểm thẳng hàng thành ba điểm thẳng hàng và bảo toàn thứ tự giữ các điểm ấy.

b) Biến đường thẳng thành đường thẳng, biến tia thành tia, biến đoạn thẳng có độ dài bằng $a$ thành đoạn thẳng có độ dài bằng $ka$.

c) Biến tam giác thành tam giác đồng dạng với tỉ số đồng dạng là $k$, biến góc thành góc bằng nó.

- Nếu một phép đồng dạng biến tam giác thành tam giác $A^{\prime }{B}^{\prime }{C}^{\prime }$ thì nó cũng biến trọng tâm, trực tâm, tâm các đường tròn nội tiếp, ngoại tiến của tam giác thành các vị trí đó trong tam giác $A^{\prime }{B}^{\prime }{C}^{\prime }$.

d) Biến đường tròn bán kính $R$ thành đường tròn bán kính $kR$.

e) Biến đa giác $n$ cạnh thành đa giác $n$ cạnh, đỉnh thành đỉnh, cạnh thành cạnh.

4. Hai hình đồng dạng

Hai hình được gọi là đồng dạng với nhau nếu có một phép đồng dạng biến hình này thành hình kia.

B. BÀI TẬP

Câu 1. Cho hai đường thẳng song song d và $d\text{'}$. Có bao nhiêu phép vị tự với tỉ số $k=20$ biến đường thẳng d thành đường thẳng $d\text{'}$?

A.  0

B.  1

C.  2

D. Vô số.

Câu 2. Cho hai đường thẳng cắt nhau d và $d\text{'}$. Có bao nhiêu phép vị tự biến d thành đường thằng $d\text{'}$?

A.  0

B.  1

C.   2

D. Vô số.

Câu 3. Trong mặt phẳng tọa độ Oxy cho ba điểm $A\left(1;2\right)$, $B\left(-3;4\right)$ và $I\left(1;1\right)$. Phép vị tự tâm I tỉ số $k=-\frac{1}{3}$ biến điểm A thành $A\text{'}$, biến điểm B thành $B\text{'}$. Mệnh đề nào sau đây là đúng?

A.  $A\text{'}B\text{'}=AB.$

B.   $\overrightarrow{A\text{'}B\text{'}}=\left(\frac{4}{3};-\frac{2}{3}\right).$

C.   $A\text{'}B\text{'}=2\sqrt{5}.$

D.   $\overrightarrow{A\text{'}B\text{'}}=\left(-4;2\right).$

Câu 4. Cho hai đường thẳng cắt nhau d và $d\text{'}$. Có bao nhiêu phép vị tự biến mỗi đường thẳng thành chính nó.

A. 0

B.  1

C.  2

D. Vô số.

Câu 5. Cho phép vị tự tỉ số k= 2 biến điểm A thành điểm B, biến điểm C thành điểm D. Mệnh đề nào sau đây đúng?

A. $\overrightarrow{AB}=2\overrightarrow{CD}.$ 

B. $2\overrightarrow{AB}=\overrightarrow{CD}.$

C. $2\overrightarrow{AC}=\overrightarrow{BD}.$

D. $\overrightarrow{AC}=2\overrightarrow{BD}.$

Câu 6. Cho tam giác ABC với trọng tâm G, D là trung điểm BC. Gọi V là phép vị tự tâm G tỉ số k biến điểm A thành điểm D. Tìm k.

A.  $k=\frac{3}{2}$

B.  $k=-\frac{3}{2}$

C.  $k=\frac{1}{2}$

D.  $k=-\frac{1}{2}$

Câu 7. Trong mặt phẳng tọa độ Oxy cho hai đường thẳng ${\Delta }_1$, ${\Delta }_2$ lần lượt có phương trình $x-2y+1=0$,  $x-2y+4=0$ và điểm $I\left(2;1\right)$. Phép vị tự tâm I tỉ số k biến đường thẳng ${\Delta }_1$ thành ${\Delta }_2$. Tìm k.

A.  k= 1

B.  k= 2

C.  k= 3

D.  k= 4

Câu 8. Trong mặt phẳng tọa độ Oxy cho đường tròn $\left(C\right):{\left(x-1\right)}^2+{\left(y-5\right)}^2=4$ và điểm $I\left(2;-3\right)$. Gọi $\left(C\text{'}\right)$ là ảnh của $\left(C\right)$  qua phép vị tự tâm I tỉ số k= -2 . Khi đó $\left(C\text{'}\right)$ có phương trình là:

 A. ${\left(x-4\right)}^2+{\left(y+19\right)}^2=16.$

B. ${\left(x-6\right)}^2+{\left(y+9\right)}^2=16.$

C. ${\left(x+4\right)}^2+{\left(y-19\right)}^2=16.$

D. ${\left(x+6\right)}^2+{\left(y+9\right)}^2=16.$

Câu 9: Trong măt phẳng Oxy cho đường thẳng d có phương trình $2x-y=0.$ Phép đồng dạng có được bằng cách thực hiện liên tiếp phép vị tự tâm O tỉ số k = -2 và phép đối xứng qua trục Oy sẽ biến d thành đường thẳng nào trong các đường thẳng sau?

A. $2x-y=0.$

B. $2x+y=0.$

C. $4x-y=0.$

D. $2x+y-2=0.$

Câu 10: Trong mặt phẳng Oxy cho đường tròn $\left(C\right)$ có phương trình ${\left(x-2\right)}^2+{\left(y-2\right)}^2=4$. Phép đồng dạng có được bằng cách thực hiện liên tiếp phép vị tự tâm O tỉ số $k=\frac{1}{2}$ và phép quay tâm O góc ${90}^0$ sẽ biến $\left(C\right)$ thành đường tròn nào trong các đường tròn sau?

A. ${\left(x–2\right)}^2+{\left(y–2\right)}^2=1$

B. ${\left(x–1\right)}^2+{\left(y–1\right)}^2=1$

C. ${\left(x+2\right)}^2+{\left(y–1\right)}^2=1$

D. ${\left(x+1\right)}^2+{\left(y–1\right)}^2=1$

Câu 11: Cho tam giác ABC và $A\text{'}B\text{'}C\text{'}$ đồng dạng với nhau theo tỉ số k. Chọn câu sai.

A. k là tỉ số hai trung tuyến tương ứng

B. k là tỉ số hai đường cao tương ứng

C. k là tỉ số hai góc tương ứng

D. k là tỉ số hai bán kính đường tròn ngoại tiếp tương ứng

Câu 12: Trong măt phẳng Oxy cho điểm $M\left(2;4\right).$ Phép đồng dạng có được bằng cách thực hiện liên tiếp phép vị tự tâm O tỉ số $k=\frac{1}{2}$ và phép đối xứng qua trục Oy sẽ biến M thành điểm nào trong các điểm sau?

A. $\left(1;2\right).$

B. $\left(-2;4\right).$

C. $\left(-1;2\right).$

D. $\left(1;-2\right).$

Câu 13: Trong mặt phẳng với hệ trục tọa độ Oxy, cho 2 đường tròn $\left(C\right)$ và $\left(C^{\text{'}}\right)$ có phương trình $x^2+y^2–4y–5=0$ và $x^2+y^2–2x+2y–14=0$. Gọi $\left(C^{\text{'}}\right)$ là ảnh của $\left(C\right)$ qua phép đồng dạng tỉ số k , khi đó giá trị k là:

A. $\frac{4}{3}$

B. $\frac{3}{4}$

C. $\frac{9}{16}$

D. $\frac{16}{9}$

Câu 14: Trong mặt phẳng với hệ trục tọa độ Oxy, cho hai Elip $\left(E_1\right)$ và $\left(E_2\right)$ lần lượt có phương trình là: $\frac{x^2}{5}+\frac{y^2}{9}=1$ và $\frac{x^2}{9}+\frac{y^2}{5}=1$. Khi đó $\left(E_2\right)$ là ảnh của $\left(E_1\right)$ qua phép đồng dạng tỉ số k bằng:

A. $\frac{5}{9}$

B. $\frac{9}{5}$

C. k = -1

D. k = 1

Câu 15: Trong mặt phẳng với hệ trục tọa độ Oxy, cho điểm $I\left(1;1\right)$ và đường tròn $\left(C\right)$ có tâm I  bán kính bằng 2. Gọi đường tròn $\left(C^{\text{'}}\right)$ là ảnh của đường tròn trên qua phép đồng dạng có được bằng cách thực hiện liên tiếp phép quay tâm O, góc $45°$ và phép vị tự tâm O, tỉ số $\sqrt{2}$. Tìm phương trình của đường tròn $\left(C^{\text{'}}\right)$?

A. $x^2+{\left(y-2\right)}^2=8$

B. ${\left(x-2\right)}^2+y^2=8$

C. ${\left(x-1\right)}^2+{\left(y-1\right)}^2=8$

D. $x^2+{\left(y-1\right)}^2=8$

Câu 16: Trong mặt phẳng Oxy cho đường tròn $\left(C\right):x^2+y^2-6x+4y-23=0,$ tìm phương trình đường tròn $\left(C^{\text{'}}\right)$ là ảnh của đường tròn $\left(C\right)$ qua phép đồng dạng có được bằng cách thực hiện liên tiếp phép tịnh tiến theo vectơ $\overrightarrow{v}=\left(3;5\right)$ và phép vị tự $V_{\left(O;-\frac{1}{3}\right)}.$ 

A. $\left(C\text{'}\right):{\left(x+2\right)}^2+{\left(y+1\right)}^2=4.$

B. $\left(C\text{'}\right):{\left(x+2\right)}^2+{\left(y+1\right)}^2=36.$

C. $\left(C\text{'}\right):{\left(x+2\right)}^2+{\left(y+1\right)}^2=6.$

D. $\left(C\text{'}\right):{\left(x-2\right)}^2+{\left(y-1\right)}^2=2.$