Với tóm tắt lý thuyết Toán lớp 7 Bài 2: Tia phân giác của một góc sách Cánh diều hay, chi tiết cùng với bài tập tự luyện chọn lọc giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán lớp 7.

Lý thuyết Toán lớp 7 Bài 2: Tia phân giác của một góc

A. Lý thuyết Tia phân giác của một góc

1. Định nghĩa

Tia phân giác của một góc là tia nằm trong góc và tạo với hai cạnh của góc đó hai góc bằng nhau.

Ví dụ:

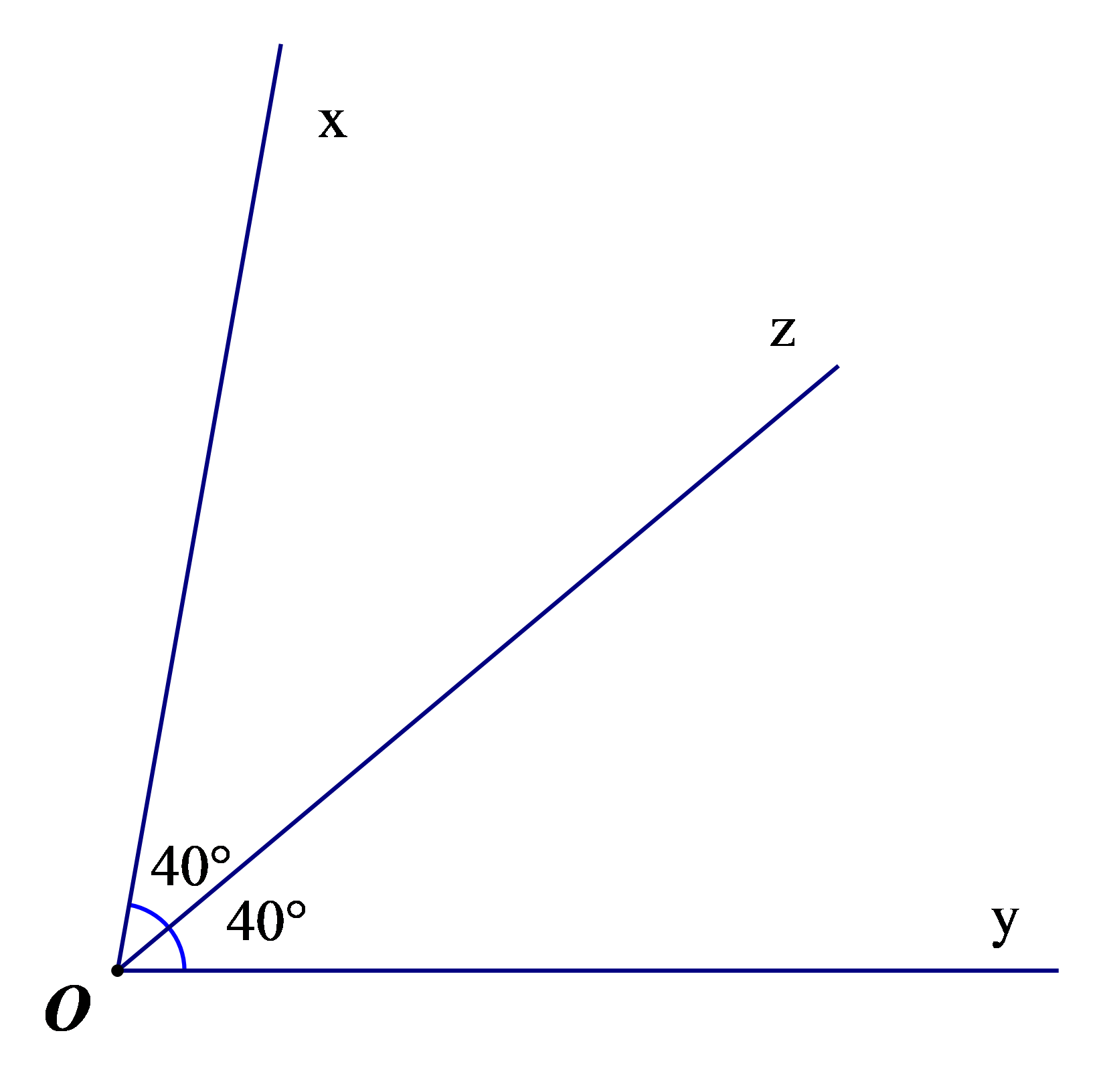Ta thấy tia Oz nằm trong góc xOy và tia Oz tạo với cạnh Ox góc xOz, tạo với cạnh Oy góc yOz; hai góc xOz và yOz đều bằng 40°.

Vì vậy, tia Oz là tia phân giác của góc xOy.

2. Vẽ tia phân giác của một góc

Cho góc xOy. Để vẽ tia phân giác của góc xOy ta có các cách sau:

Cách 1: Vẽ tia phân giác của một góc bằng thước thẳng và compa.

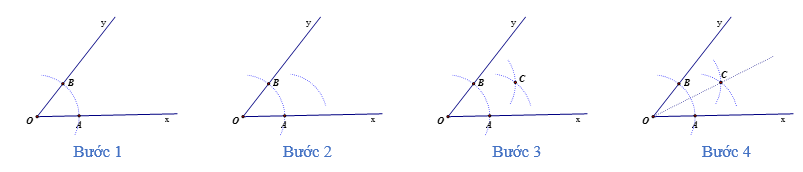
Bước 1: Trên tia Ox lấy điểm A bất kì (A khác O). Vẽ một phần đường tròn tâm O bán kính OA, cắt tia Oy tại điểm B.

Bước 2: Vẽ một phần đường tròn tâm A bán kính AO.

Bước 3: Vẽ một phần đường tròn tâm B bán kính AO, cắt phần đường tròn tâm A bán kính AO tại điểm C nằm trong góc xOy.

Bước 4: Vẽ tia OC, ta được tia phân giác của góc xOy.

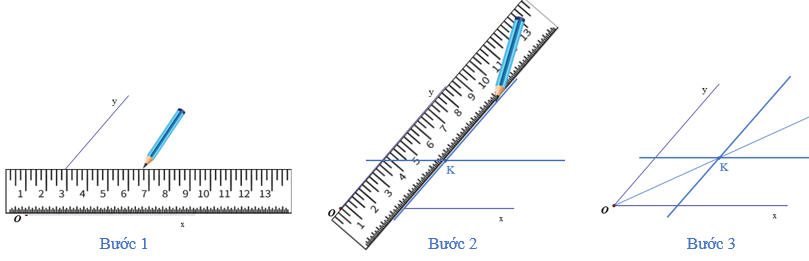
Cách 2: Dùng thước hai lề

Bước 1: Đặt thước hai lề sao cho một cạnh của thước trùng với một trong hai cạnh của góc xOy; dùng bút, vạch một vạch thẳng theo cạnh kia của thước.

Bước 2: Đặt thước hai lề sao cho một cạnh của thước trùng với cạnh còn lại của góc xOy; dùng bút, vạch một vạch thẳng theo cạnh kia của thước.

Bước 3: Hai nét vạch ở bước 1 và bước 2 cắt nhau tại điểm K nằm trong góc xOy. Vẽ tia OK, ta được tia này là tia phân giác của góc xOy.

B. Bài tập tự luyện

B.1 Bài tập tự luận

Bài 1. Cho góc xAm có số đo bằng 65° và tia Am là tia phân giác của xAy. Tính số đo góc xAy.

Hướng dẫn giải

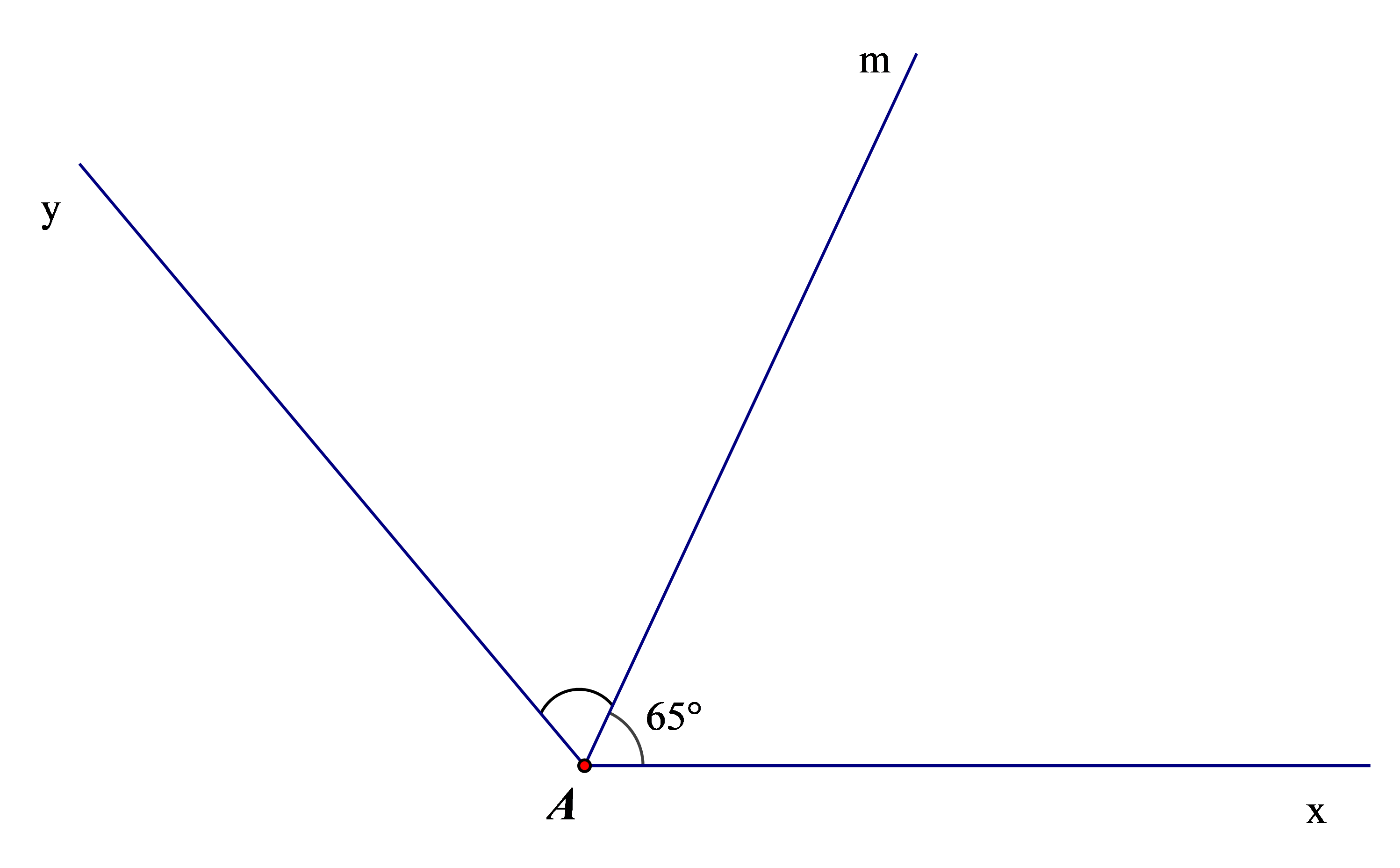Vì Am là tia phân giác của góc xAy nên:

Ta có $\widehat{xAy}=2.\widehat{xAm}=2.65°=130°$.

Vậy $\widehat{xAy}=130°$.

Bài 2. Cho góc xOy có số đo bằng 110°. Tia Oz là tia phân giác của góc xOy. Tính số đo các góc xOz và yOz.

Hướng dẫn giải

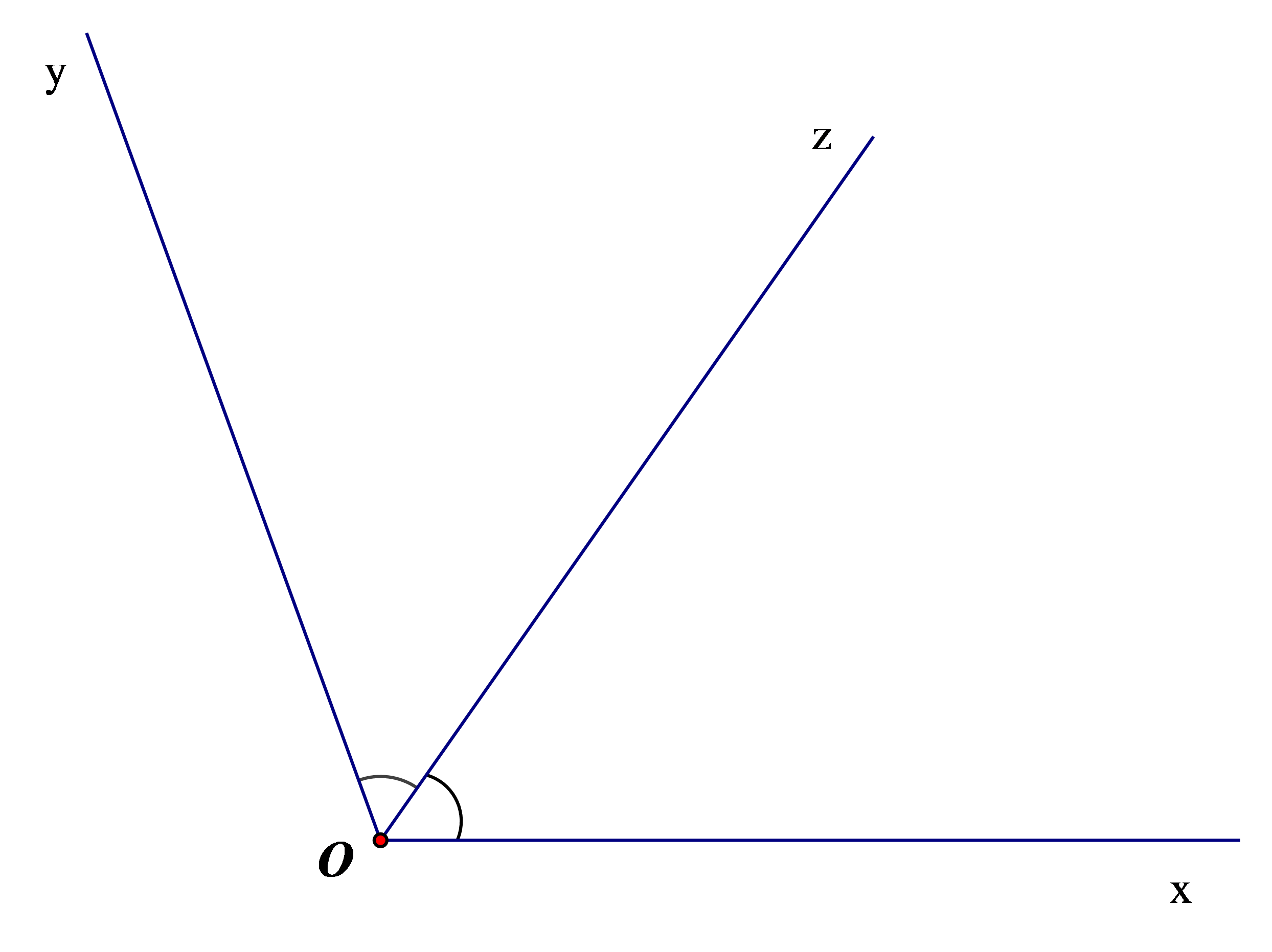Vì tia Oz là tia phân giác của góc xOy nên:

Ta có $\widehat{xOz}=\widehat{yOz}=\widehat{xOy}:2=110°:2=55°$.

Vậy $\widehat{xOz}=\widehat{yOz}=55°$.

B.2 Bài tập trắc nghiệm

Câu 1. Cho $\widehat{HOK}=90°$ và tia OI sao cho tia OK là tia phân giác của góc HOI. Khi đó góc HOI là:

A. góc vuông;                                            

B. góc nhọn;                                                                  

C. góc tù;                                                                       

D. góc bẹt.

Hướng dẫn giải

Đáp án đúng là: B

Ta có: OK là tia phân giác của góc HOI $\Rightarrow \widehat{HOK}=\widehat{KOI}=90°$.

$\Rightarrow \widehat{HOI}=\widehat{HOK}+\widehat{KOI}=90°+90°=180°$.

Vậy góc HOI là góc bẹt.

Câu 2. Tính góc xOt, biết góc xOy và góc x'Oy' là hai góc đối đỉnh, $\widehat{x\text{'}Oy\text{'}}=60°$ và tia Ot là tia phân giác góc xOy.

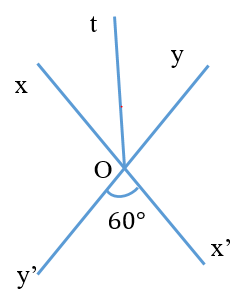
A. 60°;                                                                          

B. 120°;                                                                        

C. 42°;                                                                          

D. 30°.

Hướng dẫn giải

Đáp án đúng là: D

Ta có góc xOy và góc x'Oy' là hai góc đối đỉnh $\Rightarrow \widehat{xOy}=\widehat{x\text{'}Oy\text{'}}=60°$.

Mà Ot là tia phân giác góc xOy $\Rightarrow \widehat{xOt}=\widehat{yOt}=\frac{\widehat{xOy}}{2}=\frac{60°}{2}=30°$.

Vậy góc $\widehat{xOt}=30°$.

Câu 3. Cho các thông số như hình vẽ, Ot là tia phân giác góc zOx. Tính số đo góc zOt.

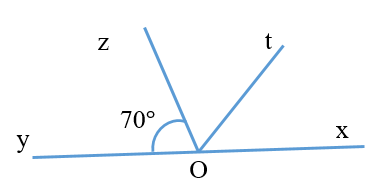A. 65°;                                                                          

B. 40°;                                                                          

C. 55°;                                                                          

D. 110°.

Hướng dẫn giải

Đáp án đúng là: C

Ta có: góc yOz và góc zOx là hai góc kề bù $\Rightarrow \widehat{yOz}+\widehat{zOx}=180°$

$\Rightarrow \widehat{zOx}=180°-\widehat{yOz}=180°-70°=110°$.

Mà Ot là tia phân giác của góc zOx nên $\widehat{zOt}=\widehat{xOt}=\frac{\widehat{zOx}}{2}=\frac{110°}{2}=55°$.

Xem thêm các bài tóm tắt lý thuyết Toán lớp 7 Cánh diều hay, chi tiết khác:

Lý thuyết Bài 1: Góc ở vị trí đặc biệt

Lý thuyết Bài 2: Tia phân giác của một góc

Lý thuyết Bài 3: Hai đường thẳng song song

Lý thuyết Bài 4: Định lý

Lý thuyết Toán 7 Chương 4: Góc. Đường thẳng song song