Với tóm tắt lý thuyết Toán lớp 7 Bài 4: Định lý sách Cánh diều hay, chi tiết cùng với bài tập tự luyện chọn lọc giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán lớp 7.
Lý thuyết Toán lớp 7 Bài 4: Định lý
A. Lý thuyết Định lý
1. Định lý
Khẳng định có các tính chất sau thì được gọi là định lý:
- Là một phát biểu về một tính chất toán học;
- Tính chất toán học đó đã được chứng tỏ là đúng không dựa vào trực giác hay đo đạc,..
Nhận xét:
+ Định lý thường được phát biểu dưới dạng “Nếu … thì …”.
+ Phần nằm giữa từ “Nếu” và từ “thì” là phần giả thiết, phần nằm sau từ “thì” là phần kết luận.
Ví dụ: Định lý: “Nếu một đường thẳng cắt hai đường thẳng song song thì hai góc so le trong bằng nhau”.
Giả thiết: Một đường thẳng cắt hai đường thẳng song song.
Kết luận: Hai góc so le trong bằng nhau.
Ta có thể vẽ hình minh họa và viết GT, KL của định lý này như sau:
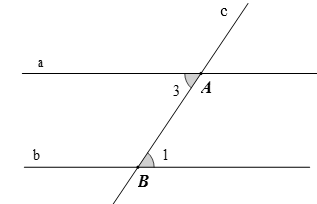
|
GT |
a // b c cắt a tại A, c cắt b tại B và là hai góc so le trong |
|
KL |
= |
2. Chứng minh định lý
Chứng minh định lý là một tiến trình lập luận từ giả thiết suy ra kết luận là đúng.
Ví dụ: Chứng minh định lý: “Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì chúng song song với nhau”.
Hướng dẫn giải
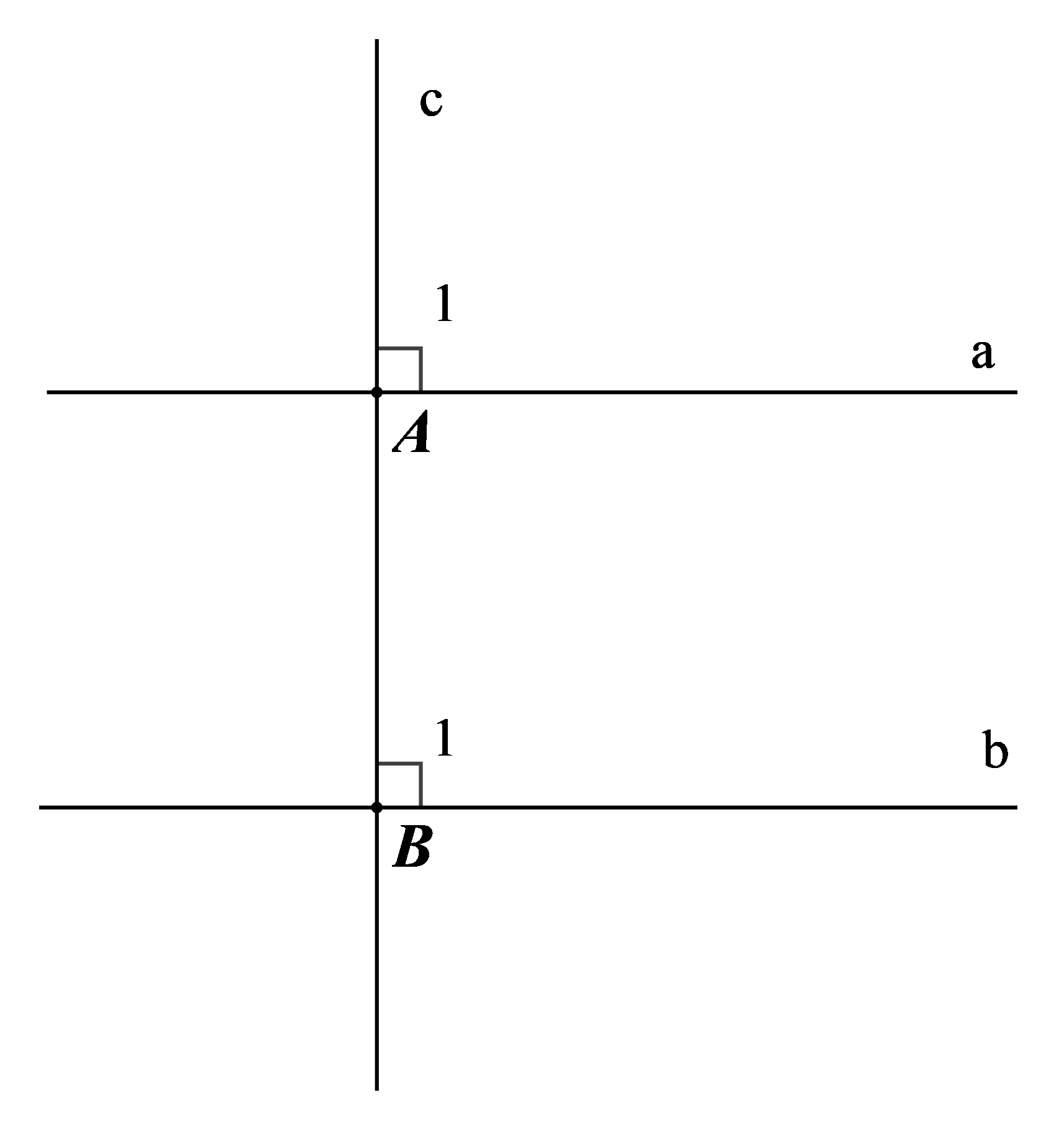
|
GT |
a và b phân biệt a ⊥ c b ⊥ c |
|
KL |
a // b |
Chứng minh
Ta có a ⊥ c suy ra ; và b ⊥ c suy ra .
Suy ra .
Mà hai góc , là hai góc đồng vị.
Vậy a // b.
B. Bài tập tự luyện
Bài 1. Cho định lý : “Nếu một đường thẳng cắt hai đường thẳng song song thì hai góc đồng vị bằng nhau”.
a) Vẽ hình minh họa nội dung định lý trên.
b) Viết giả thiết, kết luận của định lý trên.
c) Chứng minh định lý trên.
Hướng dẫn giải
a)

b)
|
GT |
a // b, c cắt a tại A, c cắt b tại B là hai góc đồng vị. |
|
KL |
|
c) Chứng minh
Qua điểm B kẻ đường thẳng b’ sao cho góc .
Khi đó đường thẳng c tạo với hai đường thẳng a và b’ hai góc đồng vị bằng nhau.
Theo dấu hiệu nhận biết hai đường thẳng song song, ta có a và b’ song song với nhau.
Suy ra qua B có hai đường thẳng b, b’ cùng song song với a.
Theo Tiên đề Euclid thì hai đường thẳng b’ và b trùng nhau.
Từ đó suy ra (vì cùng bằng ).
Bài 2. Vẽ hình minh họa và viết giả thiết, kết luận bằng kí hiệu cho định lý sau: “Một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó vuông góc với đường còn lại”.
Hướng dẫn giải
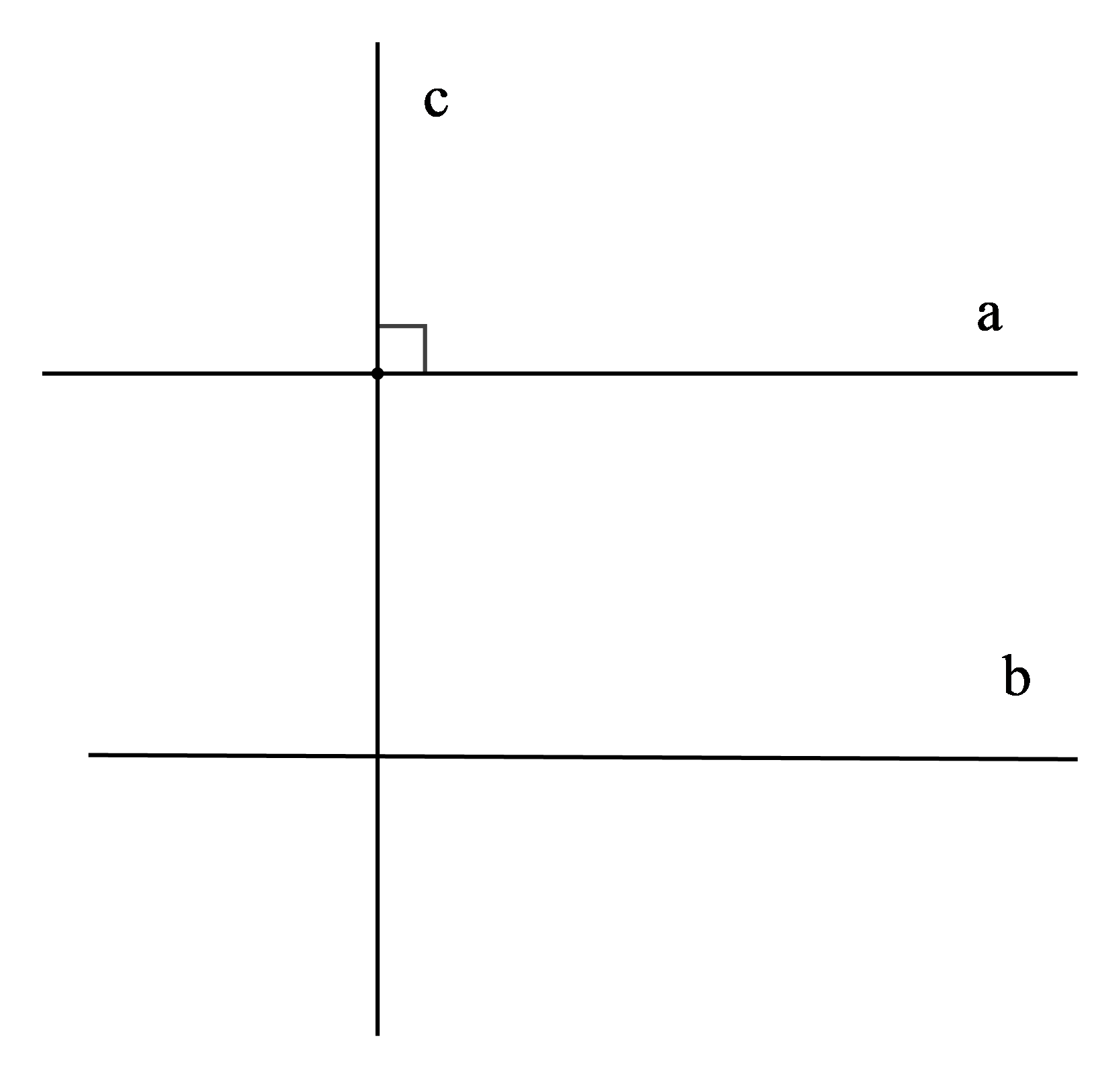
|
GT |
a // b c ⊥ a |
|
KL |
c ⊥ b |
B.2 Bài tập trắc nghiệm
Câu 1. Chọn phát biểu đúng
A. Giả thiết của định lí là điều suy ra;
B. Kết luận của định lí là điều cho biết;
C. Giả thiết của định lí là điều cho biết;
D. Cả A và B đều đúng.
Hướng dẫn giải
Đáp án đúng là: C
Giả thiết của định lí là phần cho biết. Kết luận của định lí là điều suy ra.
Câu 2. Trong định lí, phần nằm giữa từ “Nếu” và từ “thì” là phần giả thiết, vậy phần nằm sau từ “thì” là phần?
A. kết luận;
B. trả lời;
C. ý nghĩa;
D. định nghĩa.
Hướng dẫn giải
Đáp án đúng là: A
Phần nằm giữa từ “Nếu” và từ “thì” là phần giả thiết, vậy phần nằm sau từ “thì” là phần kết luận.
Câu 3. Chứng minh định lí là:
A. Dùng lập luận để từ giả thiết suy ra kết luận;
B. Dùng hình vẽ để từ giả thiết suy ra kết luận;
C. Dùng đo đạc thực tế để từ giả thiết suy ra kết luận;
D. Cả 3 đáp án đều đúng.
Hướng dẫn giải
Đáp án đúng là: A
Chứng minh định lí là dùng lập luận để từ giả thiết suy ra kết luận.
Xem thêm các bài tóm tắt lý thuyết Toán lớp 7 Cánh diều hay, chi tiết khác:
Lý thuyết Bài 3: Hai đường thẳng song song
Lý thuyết Toán 7 Chương 4: Góc. Đường thẳng song song