Với tóm tắt lý thuyết Toán lớp 7 Chương 3: Hình học trực quan sách Cánh diều hay, chi tiết cùng với bài tập tự luyện chọn lọc giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán lớp 7.
Lý thuyết Toán lớp 7 Chương 3: Hình học trực quan
A. Lý thuyết Toán 7 Chương 3: Hình học trực quan
1. Hình hộp chữ nhật. Hình lập phương.
1.1 Hình hộp chữ nhật
- Hình hộp chữ nhật có 6 mặt, 12 cạnh, 8 đỉnh, 4 đường chéo.
- Các mặt đều là hình chữ nhật.
- Các cạnh bên bằng nhau.
Chú ý: Để nhận dạng tốt hơn hình hộp chữ nhật, người ta vẽ các cạnh không nhìn thấy bằng nét đứt.
1.2. Hình lập phương
- Hình lập phương có 6 mặt, 12 cạnh, 8 đỉnh, 4 đường chéo.
- Các mặt đều là hình vuông.
- Các cạnh đều bằng nhau.
1.3. Diện tích xung quanh và thể tích của hình hộp chữ nhật và hình lập phương
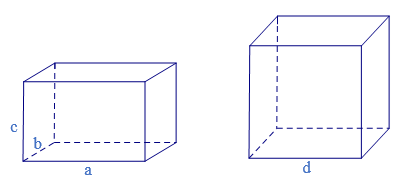
Cho hình hộp chữ nhật có ba kích thước: chiều dài a, chiều rộng là b, chiều cao là c (a, b, c cùng đơn vị đo). Cho hình lập phương có độ dài cạnh là d.
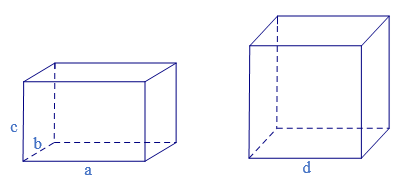
Ta có một số công thức sau:
|
|
Diện tích xung quanh |
Thể tích |
|
Hình hộp chữ nhật |
Sxq = 2(a + b)c |
V = abc |
|
Hình lập phương |
Sxq = 4d2 |
V = d3 |
2. Hình lăng trụ đứng tam giác. Hình lăng trụ đứng tứ giác
2.1 Hình lăng trụ đứng tam giác
- Hình lăng trụ đứng tam giác có 5 mặt, 9 cạnh, 6 đỉnh.
- Hai mặt đáy cùng là tam giác và nằm trong hai mặt phẳng song song với nhau; Mỗi mặt bên là hình chữ nhật;
- Các cạnh bên bằng nhau;
- Chiều cao của hình lăng trụ đứng tam giác là độ dài cạnh bên.
2.2. Hình lăng trụ đứng tứ giác
- Lăng trụ đứng tứ giác có 6 mặt, 12 cạnh, 8 đỉnh.
- Hai mặt đáy cùng là tứ giác và song song với nhau. Mỗi mặt bên là hình chữ nhật.
- Các cạnh bên bằng nhau.
- Chiều cao của hình lăng trụ đứng tứ giác là độ dài một cạnh bên.
Chú ý: Hình hộp chữ nhật và hình lập phương cũng là lăng trụ đứng tứ giác.
2.3. Thể tích và diện tích xung quanh của hình lăng trụ đứng tam giác, lăng trụ đứng tứ giác
- Thể tích của hình lăng trụ đứng tứ giác bằng diện tích đáy nhân với chiều cao.
Tức là: V = S . h, trong đó V là thể tích, S là diện tích đáy và h là chiều cao của hình lăng trụ đứng tứ giác.
- Thể tích của hình lăng trụ đứng tam giác bằng diện tích đáy nhân với chiều cao.
Tức là: V = S . h, trong đó V là thể tích, S là diện tích đáy và h là chiều cao của hình lăng trụ đứng tam giác.
- Diện tích xung quanh của hình lăng trụ đứng tam giác hay hình lăng trụ đứng tứ giác bằng chu vi đáy nhân với chiều cao.
Tức là Sxq = C . h, trong đó Sxq là diện tích xung quanh, C là chu vi đáy, h là chiều cao của hình lăng trụ đứng tam giác hay của hình lăng trụ đứng tứ giác.
B. Bài tập Toán 7 Chương 3: Hình học trực quan
B.1 Bài tập tự luận
Bài 1. Quan sát hình vẽ dưới đây và điền số và tên hình thích hợp vào bảng sau:
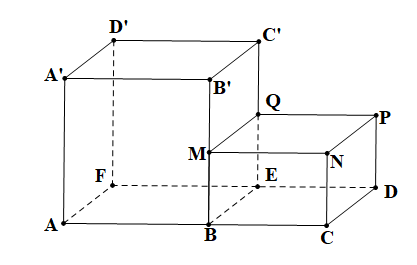
|
|
Hình lập phương |
Hình hộp chữ nhật |
|
Tên hình |
|
|
|
Tên mặt đáy |
|
|
|
Tên mặt bên |
|
|
|
Tên đỉnh |
|
|
|
Tên cạnh đáy |
|
|
|
Tên cạnh bên |
|
|
|
Tên đường chéo |
|
|
|
Cạnh bên và cạnh đáy bằng nhau không? |
|
|
Hướng dẫn giải
|
|
Hình lập phương |
Hình hộp chữ nhật |
|
Tên hình |
ABEF.A'B'C'D' |
BCDE.MNPQ |
|
Tên mặt đáy |
ABEF và A'B'C'D' |
BCDE và MNPQ |
|
Tên mặt bên |
ABB'A', BEC'B', EFD'C', AFD'A' |
BCNM, CDPN, DEQP, BEQM |
|
Tên đỉnh |
A, B, E, F, A', B', C', D' |
B, C, D, E, M, N, P, Q |
|
Tên cạnh đáy |
AB, BE, EF, FA, A'B', B'C', C'D', D'A' |
BC, ,CD, DE, EB, MN, NP, PQ, QM |
|
Tên cạnh bên |
AA', BB', EC', FD' |
BM, CN, DP, EQ |
|
Tên đường chéo |
A'E, B'F, C'A, D'B |
MD, NE, PB, QC |
|
Cạnh bên và cạnh đáy bằng nhau không? |
Có |
Không |
Bài 2. Một bể nước có thể tích bằng thể tích cùa một hình lập phương có cạnh là 160 cm. Tính thể tích của bể nước đó theo đơn vị mét khối.
Hướng dẫn giải
Đổi 160 cm = 1,6 m.
Thể tích của hình lập phương có cạnh 1,6 m là: 1,63 = 4,096 (m3).
Thể tích của bể nước là: (m3).
Vậy thể tích của bể nước là 2,4576 m3.
Bài 3. Tính diện tích xung quanh và thể tích của lăng trụ đứng tứ giác, biết đáy của nó là hình chữ nhật (độ dài các cạnh đơn vị cm).
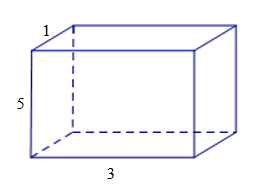
Hướng dẫn giải
Ta tính chu vi đáy C = 2(1 + 3 ) = 8 (cm), chiều cao h = 5 cm
Diện tích của hình lăng trụ đứng tứ giác này là: Sxq = C . h = 8 . 5 = 40 (cm2).
Ta tính diện tích đáy S = 1 . 3 = 3 (cm2)
Thể tích hình lăng trụ đứng tứ giác là: V = S . h = 3 . 5 = 15 (cm3).
Bài 4. Hãy kể tên các đỉnh, cạnh, mặt, chiều cao của hình lăng trụ đứng tam giác sau:.
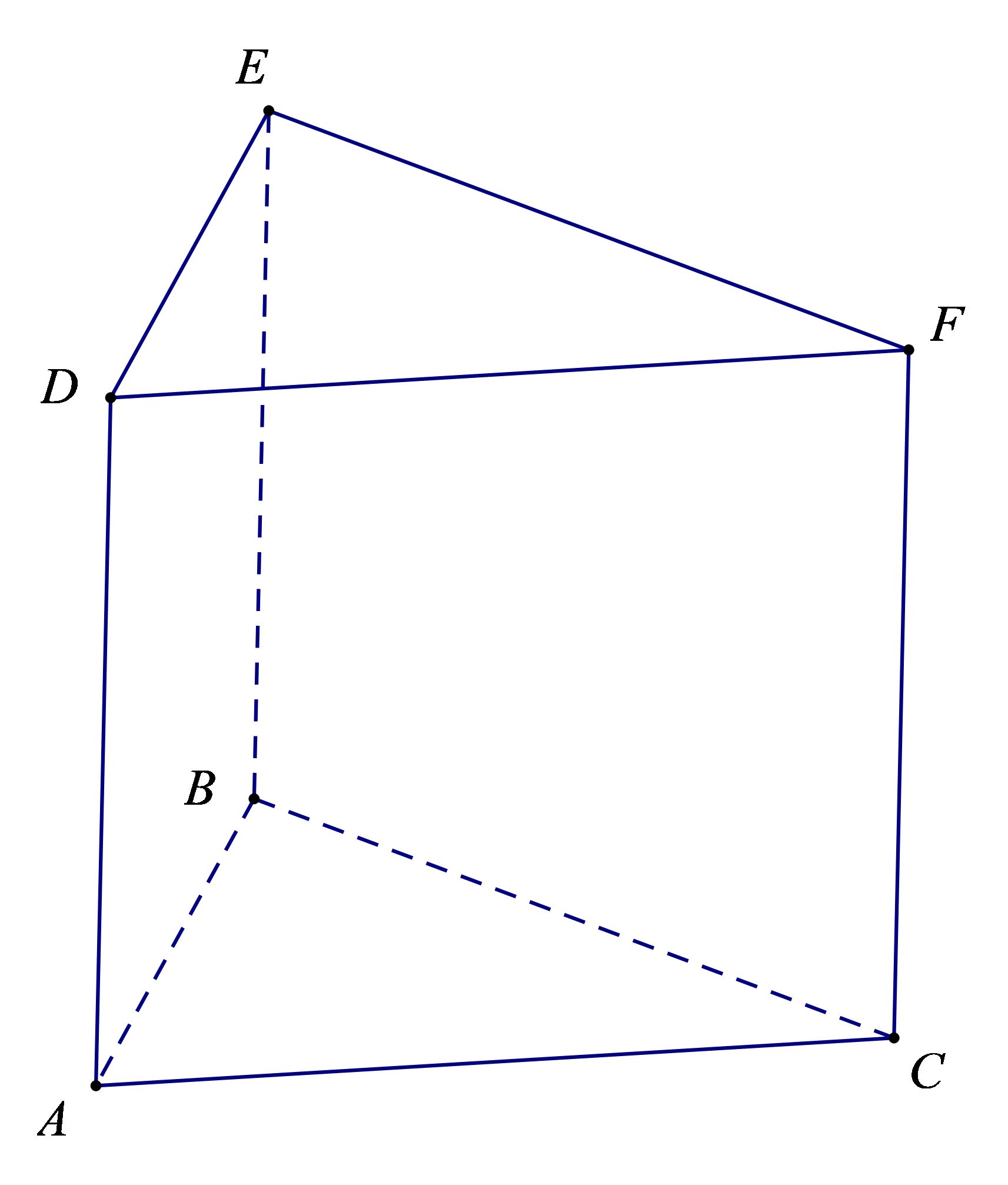
Hướng dẫn giải
Hình lăng trụ đứng tam giác ABC.DEF có:
- Các đỉnh: A, B, C, D, E, F.
- Các cạnh:
+ Cạnh đáy: AB, BC, CA, DE, EF, FD;
+ Cạnh bên: AD, BE, CF;
- Các mặt : Đáy dưới là tam giác ABC, đáy trên là tam giác DEF;
Các mặt bên là các hình chữ nhật: ADEB, BEFC, CFDA;
- Chiều cao là độ dài một cạnh bên: AD hoặc BE hoặc CF.
Bài 5. Một căn phòng dạng hình hộp chữ nhật với các kích thước của đáy dưới là 4 m; 3,5 m và chiều cao 320 cm.
a) Tính diện tích trần nhà và diện tích bốn bức tường (không tính các cửa) của căn phòng này biết diện tích cửa là 4,8 m2.
b) Người ta định sơn lại trần nhà và bốn bức tường. Biết giá thuê thợ sơn là 20 000 đồng cho 1 m2. Tính tiền công cần trả cho thợ sơn.
Hướng dẫn giải
a) Đổi 320 cm = 3,2 m.
Diện tích trần nhà hay diện tích mặt đáy là:
4. 3,5 = 14 (m2)
Diện tích xung quanh của căn phòng hình hộp chữ nhật là:
2.(4 + 3,5).3,2 = 48 (m2)
Diện tích bốn bức tường (không tính cửa) là:
48 – 4,8 = 43,2 (m2)
Vậy căn phòng có diện tích trần nhà là 14 m2 và diện tích bốn bức tường (không tính cửa) là 43,2 cm2.
b) Diện tích trần nhà và bốn bức tường (không tính cửa) là:
43,2 + 14 = 57,2 (m2)
Tiền công cần trả cho thợ sơn là:
57,2 . 20 000 = 1 144 000 (đồng).
Vậy tiền công cần trả cho thợ sơn là 1 144 000 đồng.
Bài 6. Tính diện tích xung quanh và thể tích của hình lăng trụ đứng tam giác biết, đáy của nó là tam giác vuông và các kích thước như hình vẽ (đơn vị của các cạnh là cm).
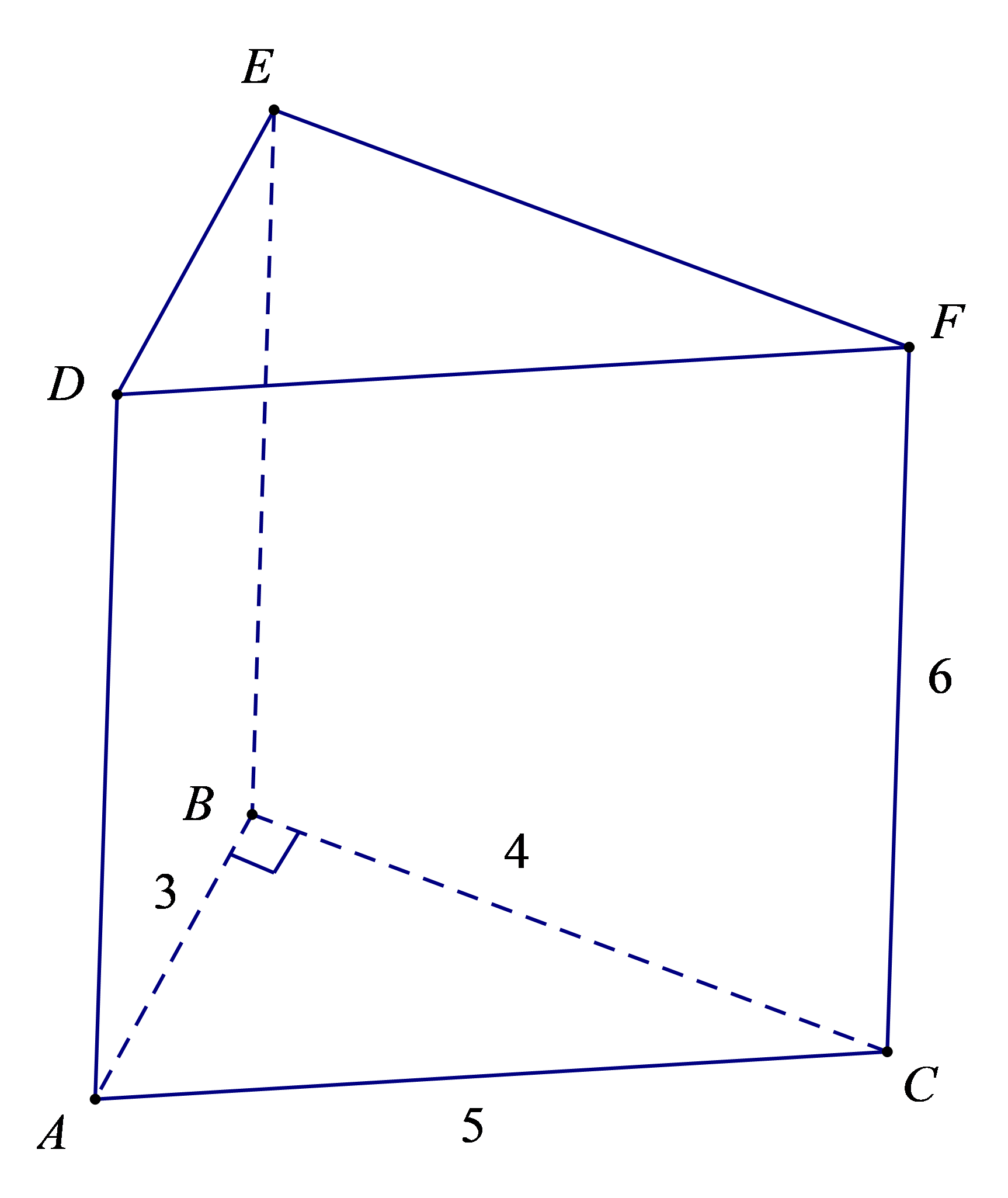
Hướng dẫn giải
Ta tính chu vi đáy là tam giác ABC: C = 3 + 4 + 5 = 12 (cm), chiều cao h = 6 cm.
Diện tích xung quanh của hình lăng trụ đứng tam giác ABC.DEF là:
Sxq = C . h = 12 . 6 = 72 (cm2).
Ta tính diện tích đáy (cm2).
Thể tích của hình lăng trụ đứng tam giác ABC.DEF là:
V = S.h = 6 . 6 = 36 (cm3).
B.2 Bài tập trắc nghiệm
Câu 1. Chọn câu sai. Hình hộp chữ nhật có:
A. 4 đường chéo;
B. 8 đỉnh;
C. 6 mặt;
D. 14 cạnh.
Hướng dẫn giải
Đáp án đúng là: D
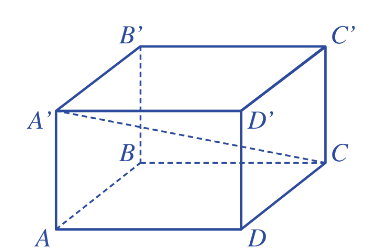
Hình hộp chữ nhật có 6 mặt, 8 đỉnh, 12 cạnh và 4 đường chéo.
Do đó, đáp án D là đáp án sai. Vậy ta chọn D.
Câu 2. Một hộp quà có dạng hình lập phương không có nắp được tô màu cả mặt trong mặt ngoài. Diện tích phải tô màu tổng cộng là 1210 cm2. Tính thể tích của hộp quà đó?
A. 1331 cm3;
B. 121 cm3;
C. 3765 cm3;
D. 144 cm3.
Hướng dẫn giải
Đáp án đúng là: A
Hộp quà hình lập phương không có nắp gồm 5 mặt là hình vuông, mỗi hình vuông có 2 mặt được tô màu nên diện tích của mỗi mặt hình vuông là 1210 : 10 = 121 (cm2).
Vì diện tích hình vuông bằng bình phương một cạnh nên cạnh của hình lập phương bằng 11 cm nên thể tích của hình lập phương bằng 113 = 1331 (cm3).
Câu 3. Một bể bơi có dạng hình hộp chữ nhật có chiều dài 9 m, chiều rộng 5 m. Mực nước trong bể cao 1,2 m một người nhảy vào bể bơi thì thể tích tăng 20 000 cm3. Hỏi thể tích của bể sau khi người nhảy vào bể bơi là:
A. 54,02 m3;
B. 42 m3;
C. 100 m3;
D. 42,02 m3.
Hướng dẫn giải
Đáp án đúng là: A
Đổi: 20 000 cm3 = 0,02 m3
Thể tích nước trong bể ban đầu có là:
V = 9.5.1,2 = 54 (m3)
Sau khi người nhảy vào bơi thể tích tăng lên 20 000 cm3 do đó thể tích của bể lúc này là:
V1 = V + 0,02 = 54,02 (m3)
Vậy thể tích của bể sau khi người đó nhảy vào bể là 54,02 (m3).
Câu 4. Thể tích hình lăng trụ đứng tam giác có đáy là tam giác vuông và có các kích thước như hình dưới đây là?
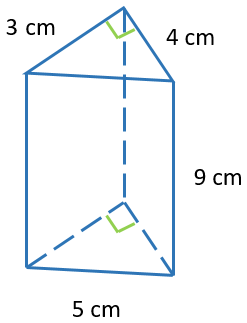
A. 52 cm3;
B. 60 cm3;
C. 72 cm3;
D. 54 cm3.
Hướng dẫn giải
Đáp án đúng là: D
Do đáy là tam giác vuông nên diện tích đáy là: (cm2)
Thể tích hình lăng trụ đứng tam giác là V = 6.9 = 54 (cm3)
Vậy thể tích hình lăng trụ đứng tam giác có đáy là V = 54 cm3.
Câu 5. Cho hình lăng trụ đứng tứ giác có diện tích xung quanh là 450 cm2, chu vi đáy là 50 cm. Chiều cao hình lăng trụ đứng tứ giác đó là:
A. 9 cm;
B. 8 cm;
C. 7 cm;
D. 6 cm.
Hướng dẫn giải
Đáp án đúng là: A
Chiều cao hình lăng trụ đứng tứ giác là:
450 : 50 = 9 (cm)
Vậy chiều cao hình lăng trụ đứng bằng 9 cm.
Xem thêm các bài tóm tắt lý thuyết Toán lớp 7 Cánh diều hay, chi tiết khác:
Lý thuyết Bài 2: Hình lăng trụ đứng tam giác. Hình lăng trụ đứng tứ giác
Lý thuyết Toán 7 Chương 3: Hình học trực quan
Lý thuyết Bài 1: Góc ở vị trí đặc biệt
Lý thuyết Bài 2: Tia phân giác của một góc
Lý thuyết Bài 3: Hai đường thẳng song song