Với tóm tắt lý thuyết Toán lớp 10 Bài 3: Nhị thức Newton sách Chân trời sáng tạo hay, chi tiết cùng với bài tập tự luyện chọn lọc giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán lớp 10.
Lý thuyết Toán lớp 10 Bài 3: Nhị thức Newton
A. Lý thuyết Nhị thức Newton
•
•
Hai công thức trên gọi là công thức nhị thức Newton (gọi tắt là nhị thức Newton) ứng với n = 4 và n = 5.
Chú ý:
– Các hệ số trong khai triển nhị thức Newton (a + b)n với n = 0; 1; 2; 3; … được viết thành từng hàng và xếp thành bảng số như dưới đây.
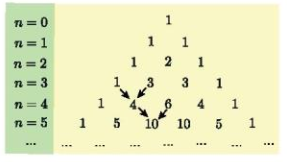
Bảng số này có quy luật: số đầu tiên và số cuối cùng của mỗi hàng đều là 1; tổng của 2 số liên tiếp cùng hàng bằng số của hàng kế dưới ở vị trí giữa hai số đó (được chỉ bởi mũi tên trên bảng).
Bảng số trên dược gọi là tam giác Pascal (đặt theo tên của nhà toán học, vật lí học, triết học người Pháp Blaise Pascal, 1623 – 1662).
Ví dụ: Sử dụng công thức nhị thức Newton khai triển biểu thức (a + 2)4.
Hướng dẫn giải
Theo công thức nhị thức Newton ta có:
(a + 2)4 = 1.a4 + 4a3.2 + 6a2.22 + 4a.23 + 24
= a4 + 8a3 + 24a2 + 32a + 16.
Ví dụ: Khai triển và rút gọn biểu thức:
Hướng dẫn giải
Theo công thức nhị thức Newton ta có:
•
•
Do đó ta có:
B. Bài tập tự luyện
Bài 1. Sử dụng công thức nhị thức Newton khai triển biểu thức:
a) (2x + y)4;
b)
Hướng dẫn giải
Theo công thức nhị thức Newton ta có:
a) (2x + y)4 = (2x)4 + 4.(2x)3.y + 6.(2x)2.y2 + 4(2x).y3 + y4
= 16x4 + 32x3y + 24x2y2 + 8xy3 + y4.
b)
Bài 2. Tìm hệ số của x4 trong khai triển (2x – 3)5.
Hướng dẫn giải
Theo công thức nhị thức Newton ta có:
(2x + 3)5 = (2x)5 + 5(2x)4.(–3) + 10.(2x)3.(–3)2 + 10.(2x)2.(–3)3 + 5.2x.(–3)4 + (–3)5
= 32x5 – 240x4 + 720x3 – 1080x2 + 810x – 243
Vậy hệ số của x4 trong khai triển là –240.
Bài 3. Sử dụng công thức nhị thức Newton chứng tỏ rằng:
Hướng dẫn giải
Giả sử ta có khai triển (a + b)n với n = 0; 1; 2; …
Ta thấy trong biểu thức chứng minh có tổ hợp chập k của 5, nên n = 5.
Ở đây có xuất hiện lũy thừa của số 2 từ mũ 1 đến mũ 5 nên b = 2.
Ta có khai triển:
Khi x = 1 thì ta có:
Vậy
Bài 4. Khai triển và rút gọn biểu thức: (x + 2)4 + (2 – x)4.
Từ đó tính giá trị biểu thức: 2,054 + 1,954.
Hướng dẫn giải
Theo công thức nhị thức Newton ta có:
• (x + 2)4 = x4 + 4x3.2 + 6x2.22 + 4x.23 + 24
= x4 + 8x3 + 24x2 + 32x + 16.
• (2 – x)4 = 24 + 4.23.(–x) + 6.22.(–x)2 + 4.2.(–x)3 + (–x)4
= x4 – 8x3 + 24x2 – 32x + 16.
Do đó ta có:
(x + 2)4 + (2 – x)4 = 2x4 + 48x2 + 32.
Với x = 0,05 ta có:
(0,05 + 2)4 + (2 – 0,05)4
= 2.(0,05)4 + 48.(0,05)2 + 32
= 32,1200125.
Vậy 2,054 + 1,954 = 32,1200125.
Xem thêm các bài tóm tắt lý thuyết Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:
Lý thuyết Bài 2: Hoán vị, chỉnh hợp và tổ hợp
Lý thuyết Bài 3: Nhị thức Newton
Lý thuyết Bài 1: Tọa độ của vectơ
Lý thuyết Bài 2: Đường thẳng trong mặt phẳng tọa độ
Lý thuyết Bài 3: Đường tròn trong mặt phẳng tọa độ