Bộ 21 Đề thi Toán lớp 7 Học kì 2 năm 2024 có đáp án – Đề 1

Phòng Giáo dục và Đào tạo .....

Đề thi Học kì 2 - Năm học 2024 - 2025

Bài thi môn: Toán lớp 7

Thời gian làm bài: 90 phút

(Đề 1)

I. Trắc nghiệm (3,0 điểm) Khoanh tròn vào chữ cái đứng trước câu trả lời đúng

Câu 1. Biểu thức nào sau đây không là đơn thức?

A. 4x²y(-2x).

B. 2x.

C. 2xy - x².

D. 2021.

Câu 2. Bậc của đơn thức -2x³y⁵ là:

A. -2.

B. 3.

C. 8.

D. x³y⁵.

Câu 3. Bậc của đa thức A = x²y⁴ - x³y⁵ - x⁷ + 9 là:

A. 6.

B. 7.

C. 8.

D. 9.

Câu 4. Cho tam giác ABC cân tại A có \[\widehat A = 40^\circ .\] Số đo góc B là:

A. 50^o.

B. 60^o.

C. 70^o.

D. 80^o.

Câu 5. Giao điểm 3 đường cao của một tam giác gọi là:

A. trọng tâm của tam giác.

B. trực tâm của tam giác.

C. tâm đường tròn ngoại tiếp tam giác.

D. điểm cách đều 3 cạnh của tam giác.

Câu 6. Cho tam giác ABC cân tại A có AB = 5 cm, BC = 6 cm và AM là đường trung tuyến. Độ dài đoạn AM là:

A. 3 cm.

B. \[\sqrt {61} \] cm.

C. \[\sqrt {11} \] cm.

D. 4 cm.

II. Tự luận (7,0 điểm)

Bài 1. (1,5 điểm)

a) Tính giá trị biểu thức: 4x³ - 3xy tại x = \[\frac{{ - 1}}{2}\]; y = 6.

b) Cho đơn thức A = (-3xy) . \[\left( {\frac{2}{3}{x^2}y} \right)\]. Hãy thu gọn đơn thức và chỉ ra hệ số, phần biến của đơn thức A.

Bài 2. (2,0 điểm) Tìm tất cả nghiệm của mỗi đa thức sau:

a) A = 2(-x + 5) - \[\frac{3}{2}\](x - 4).

b) B = -4x² + 9.

c) C = x³ + 4x.

Bài 3. (3,0 điểm) Cho tam giác ABC vuông tại A, AB = 3 cm, BC = 5 cm. Trên cạnh BC lấy điểm D sao cho BD = 3 cm. Đường thẳng vuông góc với BC tại D cắt cạnh AC tại M, cắt tia BA tại N.

a) Tính AC và so sánh các góc của tam giác ABC.

b) Chứng minh MA = MD và tam giác MNC cân.

c) Gọi I là trung điểm của CN. Chứng minh ba điểm B, M, I thẳng hàng.

Bài 4. (0,5 điểm) Tính giá trị của biểu thức \[\frac{{4{\rm{a}} - b}}{{3{\rm{a}} + 3}} + \frac{{4b - a}}{{3b - 3}}\] với a - b = 3; a ≠ -1; b ≠ 1.

Đáp án và hướng dẫn giải

I. Trắc nghiệm (3,0 điểm) Khoanh tròn vào chữ cái đứng trước câu trả lời đúng

Câu 1. Biểu thức nào sau đây không là đơn thức?

A. 4x²y(-2x).

B. 2x.

C. 2xy - x².

D. 2021.

Hướng dẫn giải

Đáp án đúng là: C

2xy - x² là đa thức nên chọn đáp án C.

Câu 2. Bậc của đơn thức -2x³y⁵ là:

A. -2.

B. 3.

C. 8.

D. x³y⁵.

Hướng dẫn giải

Đáp án đúng là: C

Bậc của đơn thức -2x³y⁵ là 3 + 5 = 8 nên chọn đáp án C.

Câu 3. Bậc của đa thức A = x²y⁴ - x³y⁵ - x⁷ + 9 là:

A. 6.

B. 7.

C. 8.

D. 9.

Hướng dẫn giải

Đáp án đúng là: C

Bậc của đa thức A = x²y⁴ - x³y⁵ - x⁷ + 9 là bậc của hạng tử - x³y⁵.

Bậc của hạng tử - x³y⁵ là: 3 + 5 = 8 nên chọn đáp án C.

Câu 4. Cho tam giác ABC cân tại A có \[\widehat A = 40^\circ .\] Số đo góc B là:

A. 50^o.

B. 60^o.

C. 70^o.

D. 80^o.

Hướng dẫn giải

Đáp án đúng là: C

Cho tam giác ABC cân tại A nên \[\widehat B = \widehat C\], mà \[\widehat A + \widehat B + \widehat C = 180^\circ \] nên \[\widehat A + 2\widehat B = 180^\circ \]

Do đó \[\widehat B = \frac{{180^\circ  - \widehat A}}{2} = \frac{{180^\circ  - 40^\circ }}{2}\] = 70^o.

Chọn đáp án C.

Câu 5. Giao điểm 3 đường cao của một tam giác gọi là:

A. trọng tâm của tam giác.

B. trực tâm của tam giác.

C. tâm đường tròn ngoại tiếp tam giác.

D. điểm cách đều 3 cạnh của tam giác.

Hướng dẫn giải

Đáp án đúng là: B

Giao điểm 3 đường cao của một tam giác gọi là trực tâm của tam giác (theo định nghĩa) nên chọn đáp án B.

Câu 6. Cho tam giác ABC cân tại A có AB = 5 cm, BC = 6 cm và AM là đường trung tuyến. Độ dài đoạn AM là:

A. 3 cm.

B. \[\sqrt {61} \] cm.

C. \[\sqrt {11} \] cm.

D. 4 cm.

Hướng dẫn giải

Đáp án đúng là: D

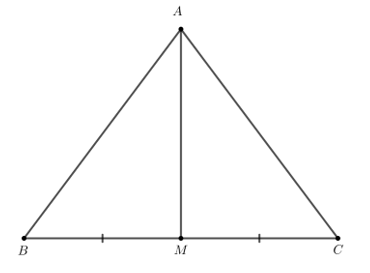
\[\Delta ABC\] cân tại A có AM là đường trung tuyến nên AM vừa là đường trung tuyến, vừa là đường cao của \[\Delta ABC\].

Do AM là đường trung tuyến nên M là trung điểm của BC.

Do đó BM = \[\frac{1}{2}\]BC = \[\frac{1}{2}\].6 = 3 cm.

Áp dụng định lý Pytago vào \[\Delta ABM\] vuông tại M có:

AM² + BM² = AB²

\[ \Rightarrow \] AM² = AB² - BM²

\[ \Rightarrow \] AM² = 5² - 3²

\[ \Rightarrow \] AM² = 25 - 9

\[ \Rightarrow \] AM² = 16

\[ \Rightarrow \] AM = 4 cm

Chọn đáp án D.

II. Tự luận (7,0 điểm)

Bài 1. (1,5 điểm)

a) Với x = \[\frac{{ - 1}}{2}\]; y = 6 thì 4x³ - 3xy = 4.\[{\left( {\frac{{ - 1}}{2}} \right)^3}\] - 3. \[\left( {\frac{{ - 1}}{2}} \right)\].6

= 4.\[\frac{{{{\left( { - 1} \right)}^3}}}{{{2^3}}}\] - 3.(-3) = 4. \[\left( {\frac{{ - 1}}{8}} \right)\] + 9 = (-2) + 9 = 7.

Vậy 4x³ - 3xy = 7 tại x = \[\frac{{ - 1}}{2}\]; y = 6.

b) A = (-3xy) . \[\left( {\frac{2}{3}{x^2}y} \right)\]

A = \[\left( { - 3.\frac{2}{3}} \right)\].(x.x²).(y.y)

A = -2x³y².

Hệ số của đơn thức A: -2.

Phần biến của đơn thức A: x³y².

Bài 2. (2,0 điểm)

a) A = 2(-x + 5) - \[\frac{3}{2}\](x - 4)

A = 2.(-x) + 2.5 - \[\frac{3}{2}\]x + \[\frac{3}{2}.4\]

A = (-2x) + 10 - \[\frac{3}{2}x\] + 6

A = (-2 - \[\frac{3}{2}\])x + 16

A = \[\left( { - \frac{4}{2} - \frac{3}{2}} \right)\]x + 16

A = \[\frac{{ - 7}}{2}\]x + 16

Để A = 0 thì \[\frac{{ - 7}}{2}\]x + 16 = 0

\[ \Rightarrow \frac{{ - 7}}{2}\]x = - 16

\[ \Rightarrow \] x = \[ - 16:\left( {\frac{{ - 7}}{2}} \right)\]

\[ \Rightarrow \] x = \[ - 16.\left( {\frac{2}{{ - 7}}} \right)\]

\[ \Rightarrow \] x = \[\frac{{32}}{7}\]

Vậy x = \[\frac{{32}}{7}\].

b) B = -4x² + 9

Để B = 0 thì -4x² + 9 = 0

\[ \Rightarrow \] -4x² = -9

\[ \Rightarrow \] x² = \[\frac{9}{4}\]

Trường hợp 1. x² = \[{\left( {\frac{3}{2}} \right)^2}\]

\[ \Rightarrow x = \frac{3}{2}\]

Trường hợp 2. x² = \[{\left( { - \frac{3}{2}} \right)^2}\]

\[ \Rightarrow x =  - \frac{3}{2}\]

Vậy x = \[\frac{3}{2}\] hoặc x = \[ - \frac{3}{2}\].

c) C = x³ + 4x

C = x(x² + 4)

Do x² ≥ 0 với mọi x nên x² + 4 > 0 với mọi x.

Do đó C = 0 khi x = 0.

Vậy x = 0.

Bài 3. (3,0 điểm)

 

a) Áp dụng định lý Pytago vào tam giác ABC vuông tại A:

AB² + AC² = BC²

\[ \Rightarrow \] 3² + AC² = 5²

\[ \Rightarrow \] AC² = 25 - 9

\[ \Rightarrow \] AC² = 16

\[ \Rightarrow \] AC = 4 cm.

\[\Delta ABC\] vuông tại A nên \[\widehat {BAC}\] là góc lớn nhất trong \[\Delta ABC.\]

AB < AC nên \[\widehat {ACB} < \widehat {ABC}\].

Vậy \[\widehat {ACB} < \widehat {ABC} < \widehat {BAC}.\]

b) Xét \[\Delta ABM\] vuông tại A và \[\Delta DBM\] vuông tại D có:

AB = BD (theo giả thiết)

BM chung.

\[ \Rightarrow \Delta ABM = \Delta DBM\] (cạnh huyền - cạnh góc vuông).

\[ \Rightarrow \] MA = MD (2 cạnh tương ứng).

Xét \[\Delta AMN\] vuông tại A và \[\Delta DMC\] cân tại D có:

AM = DM (chứng minh trên).

\[\widehat {AMN} = \widehat {DMC}\] (2 góc đối đỉnh).

\[ \Rightarrow \Delta AMN = \Delta DMC\] (góc nhọn - cạnh góc vuông).

\[ \Rightarrow \] MN = MC (2 cạnh tương ứng).

\[\Delta MNC\] có MN = MC nên \[\Delta MNC\] cân tại M.

c) Xét \[\Delta BCN\] có \[CA \bot BN;\] \[N{\rm{D}} \bot BC\].

Mà CA cắt ND tại M nên M là trực tâm của \[\Delta BCN\].

Do đó \[BM \bot NC\](1).

\[\Delta MNC\] cân tại M, lại có I là trung điểm của NC nên \[MI \bot NC\] (2).

Từ (1) và (2) suy ra B, M, I thẳng hàng.

Vậy B, M, I thẳng hàng.

Bài 4. (0,5 điểm)

\[\frac{{4{\rm{a}} - b}}{{3{\rm{a}} + 3}} + \frac{{4b - a}}{{3b - 3}} = \frac{{3{\rm{a}} + a - b}}{{3{\rm{a}} + 3}} + \frac{{4b - a}}{{3b - \left( {a - b} \right)}}\]

\[ = \frac{{3{\rm{a}} + 3}}{{3{\rm{a}} + 3}} + \frac{{4b - a}}{{3b - a + b}} = 1 + \frac{{4b - a}}{{4b - a}}\]= 1 + 1 = 2.

 

Bộ 21 Đề thi Toán lớp 7 Học kì 2 năm 2024 có đáp án – Đề 2

Phòng Giáo dục và Đào tạo .....

Đề thi Học kì 2 - Năm học 2024 - 2025

Bài thi môn: Toán lớp 7

Thời gian làm bài: 90 phút

(Đề 2)

Câu 1: (2.0 điểm) Điểm kiểm tra một tiết môn Toán của học sinh một lớp 7 tại một trường THCS được cho trong bảng “tần số” sau:

 

a) Dấu hiệu điều tra ở đây là gì?

b) Có bao nhiêu học sinh làm kiểm tra? Số các giá trị khác nhau?

c) Tìm mốt của dấu hiệu và tính số trung bình cộng.

 

Câu 2: (1.0 điểm) Thu gọn và tìm bậc của các đơn thức sau:

a) \(A = \left( {2{x^3}y} \right).\left( { - 3xy} \right)\);                                

b) \(B = \left( { - \frac{1}{{16}}{x^2}{y^2}} \right).\left( {4{x^3}} \right).\left( {8xyz} \right)\).

Câu 3: (1.0 điểm) Tìm đa thức M biết:

a) \(M - \left( {{x^2}y - 1} \right) =  - 2{x^3} + {x^2}y + 1\);

b) \(3{x^2} + 3xy - {x^3} - M = 3{x^2} + 2xy - 4{y^2}\).

Câu 4: (2.0 điểm) Cho các đa thức sau: \(P(x) = {x^3} + 3{x^2} + 3x - 2\) và\(Q(x) =  - {x^3} - {x^2} - 5x + 2\)

a) Tính \(P(x) + Q(x)\);

b) Tính \(P(x) - Q(x)\);

c) Tìm nghiệm của đa thức H(x) biết \(H(x) = P(x) + Q(x)\).

Câu 5: (1.0 điểm) Cho hai đa thức \(f\left( x \right) = 2{x^2} + ax + 4\) và \(g\left( x \right) = {x^2} - 5x - b\) (a, b là hằng số). Tìm các hệ số a, b sao cho \(f\left( 1 \right) = g(2)\) và \(f\left( { - 1} \right) = g(5)\).

Câu 6: (3.0 điểm) Cho \[\Delta ABC\]vuông tại A, có AB = 6cm, AC = 8cm.

a) Tính độ dài cạnh BC và chu vi tam giác ABC;

b) Đường phân giác của góc B cắt AC tại D. Vẽ \[DH \bot BC\,\left( {H \in BC} \right)\].

Chứng minh: \[\Delta ABD = \Delta HBD\];

c) Chứng minh: DA < DC.

----------HẾT---------

Đáp án và hướng dẫn giải

Câu 1:

a) Dấu hiệu điều tra: “Điểm kiểm tra 1 tiết môn Toán của mỗi học sinh trong một lớp 7”.  (0,5 điểm)

b) Có 40 học sinh làm kiểm tra. Có 8 giá trị khác nhau. (0,5 điểm)

c) Mốt của dấu hiệu: 8 (dấu hiệu có tần số lớn nhất: 11). (0,5 điểm)

Số trung bình cộng \(\overline X  = \frac{{3.1 + 4.2 + 5.7 + 6.8 + 7.5 + 8.11 + 9.4 + 10.2}}{{40}} = \frac{{273}}{{40}} = 6,825\).

(0,5 điểm)

Câu 2:

a)

\(A = \left( {2{x^3}y} \right).\left( { - 3xy} \right) = \left( {2.\left( { - 3} \right)} \right).\left( {{x^3}.x} \right).\left( {y.y} \right) =  - 6{x^4}{y^2}\).  (0,25 điểm)

Đơn thức có bậc là 4 + 2 = 6.              (0,25 điểm)

b)

\(B = \left( { - \frac{1}{{16}}{x^2}{y^2}} \right).\left( {4{x^3}} \right).\left( {8xyz} \right)\).

\(\begin{array}{l} = \left( {\frac{{ - 1}}{{16}}.4.8} \right).\left( {{x^2}.{x^3}.x} \right).\left( {{y^2}.y} \right).z\\ =  - 2{x^6}{y^3}z\end{array}\)     (0,25 điểm)

Đơn thức có bậc là 6 + 3 + 1 = 10.           (0,25 điểm)

Câu 3:

a)

\(M - \left( {{x^2}y - 1} \right) =  - 2{x^3} + {x^2}y + 1\)

\(\begin{array}{l}M = \left( { - 2{x^3} + {x^2}y + 1} \right) + \left( {{x^2}y - 1} \right)\\M =  - 2{x^3} + 2{x^2}y\end{array}\)  (0,5 điểm)

b)

\(3{x^2} + 3xy - {x^3} - M = 3{x^2} + 2xy - 4{y^2}\) 

\(M = \left( {3{x^2} + 3xy - {x^3}} \right) - \left( {3{x^2} + 2xy - 4{y^2}} \right)\)

\(\begin{array}{l}M = \left( {3{x^2} - 3{x^2}} \right) + \left( {3xy - 2xy} \right) - {x^3} + 4{y^2}\\M = xy - {x^3} + 4{y^2}\end{array}\) (0,5 điểm)

Câu 4:

a) \(P(x) = {x^3} + 3{x^2} + 3x - 2\) ; \(Q(x) =  - {x^3} - {x^2} - 5x + 2\)

\(P(x) + Q(x) = \left( {{x^3} + 3{x^2} + 3x - 2} \right) + \left( { - {x^3} - {x^2} - 5x + 2} \right)\)

\(\begin{array}{l} = \left( {{x^3} - {x^3}} \right) + \left( {3{x^2} - {x^2}} \right) + \left( {3x - 5x} \right) + \left( { - 2 + 2} \right)\\ = 2{x^2} - 2x\end{array}\)             (0,75 điểm)

b) \(P(x) - Q(x) = \left( {{x^3} + 3{x^2} + 3x - 2} \right) - \left( { - {x^3} - {x^2} - 5x + 2} \right)\)

\( = \left( {{x^3} + {x^3}} \right) + \left( {3{x^2} + {x^2}} \right) + \left( {3x + 5x} \right) + \left( { - 2 - 2} \right)\)

\( = 2{x^3} + 4{x^2} + 8x - 4\)                         (0,75 điểm)

c) Ta có: H(x) = 2x² – 2x

H(x) = 0 khi

 \(2{x^2} - 2x = 0\)

\( \Rightarrow 2x\left( {x - 1} \right) = 0\)

Suy ra \(\left[ \begin{array}{l}x = 0\\x = 1\end{array} \right.\)

Vậy nghiệm của đa thức H(x) là x = 0; x = 1.               (0,5 điểm)

Câu 5:

Theo đề bài ta có:

\(f\left( 1 \right) = g(2) \Rightarrow 6 + a =  - 6 - b \Rightarrow a + b =  - 12\)  (1)                        (0,25 điểm)

\(f\left( { - 1} \right) = g(5) \Rightarrow 6 - a =  - b \Rightarrow b = a - 6\) (2)           (0,25 điểm)

Thay (2) vào (1) ta được:

\(a + a - 6 =  - 12 \Rightarrow a =  - 3\)                                    

\( \Rightarrow b = a - 6 =  - 3 - 6 =  - 9\)                       (0,25 điểm)

Vậy \(a =  - 3;\,b =  - 9\).                 (0,25 điểm)

Câu 6:

a) Vẽ hình đúng, ghi GT, KL được 0,5 điểm

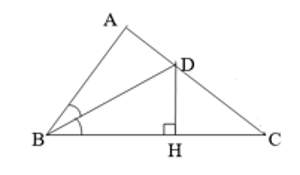
Áp dụng định lí Py–ta–go vào tam giác vuông ABC ta có:

\(B{C^2} = A{C^2} + A{B^2} = {6^2} + {8^2} = 100 \Rightarrow BC = 10\)cm                   (0,5 điểm)

Chu vi tam giác ABC: AB + AC + BC = 6 + 8 + 10 = 24 cm    (0,5 điểm)

b) Xét hai tam giác vuông ABD và HBD có:

BD là cạnh chung

\[\widehat {ABD} = \widehat {HBD}\] (BD là tia phân giác của góc B)

Do đó: \[\Delta ABD = \Delta HBD\] (cạnh huyền – góc nhọn)                           (1 điểm)

c) Từ câu b) \[\Delta ABD = \Delta HBD\]suy ra DA = DH (hai cạnh tương ứng) (1)

Xét tam giác vuông DHC có: DC > DH (DC là cạnh huyền) (2)

Từ (1) và (2) suy ra: DC > DA   (0,5 điểm)

-----------------------

 

 

Bộ 21 Đề thi Toán lớp 7 Học kì 2 năm 2024 có đáp án – Đề 3

Phòng Giáo dục và Đào tạo .....

Đề thi Học kì 2 - Năm học 2024 - 2025

Bài thi môn: Toán lớp 7

Thời gian làm bài: 90 phút

(Đề 3)

Bài 1 : (2,0 điểm) Thời gian giải một bài toán (tính theo phút) của 30 học sinh được ghi lại trong bảng dưới đây :

a) Dấu hiệu ở đây là gì ? Số các giá trị là bao nhiêu ?

b) Lập bảng “tần số”.

c) Tính số trung bình cộng (làm tròn một chữ số thập phân) và mốt của dấu hiệu.

Bài 2: (2,0 điểm) Cho đơn thức A = \[\left( { - \frac{2}{5}{x^3}{y^4}} \right).\left( {\frac{5}{6}x{y^2}z} \right).\]

a) Thu gọn đơn thức A.

b) Xác định hệ số và bậc của đơn thức.

Bài 3: (2,0 điểm) Cho hai đa thức f(x) = 5 + 3x² - x - 2x² và g(x) = 3x + 3 - x - x².

a) Thu gọn và sắp xếp hai đa thức theo lũy thừa giảm dần của biến.

b) Tính h(x) = f(x) + g(x).

Bài 4: (3,5 điểm) Cho tam giác ABC cân (AB = AC). Các đường phân giác BE, CF cắt nhau tại H.

a) Chứng minh \[\Delta AB{\rm{E  =  }}\Delta ACF.\]

b) Tia AH cắt BC tại D. Chứng minh D là trung điểm của BC và EF // BC.

c) Chứng minh AH là trung trực của EF. So sánh HF và HC.

d) Tìm điều kiện của tam giác ABC để HC = 2.HD.

Bài 5: (0,5 điểm) Cho đa thức f(x) thỏa mãn f(x) + x.f(-x) = x + 1 với mọi giá trị của x. Tính f(1).

 

Đáp án và hướng dẫn giải

Bài 1: (2,0 điểm)

a) - Dấu hiệu ở đây là thời gian giải một bài toán (tính theo phút) của 30 học sinh.

- Số các giá trị là 30.

b) Ta có bảng tần số:

Giá trị (x)	5	6	7	8	9	12
Tần số (n)	2	3	9	7	6	3	N = 30

c) Trung bình cộng của dấu hiệu bằng:

\[\frac{{5.2 + 6.3 + 7.9 + 8.7 + 9.6 + 12.3}}{{2 + 3 + 9 + 7 + 6 + 3}} = \frac{{237}}{{30}} = \frac{{79}}{{10}} = 7,9\]

Mốt của dấu hiệu bằng 7.

Bài 2: (2,0 điểm)

a) A = \[\left( { - \frac{2}{5}{x^3}{y^4}} \right).\left( {\frac{5}{6}x{y^2}z} \right)\]

A = \[\left( { - \frac{2}{5}.\frac{5}{6}} \right)\] . (x³ . x) . (y⁴ . y² ) . z

A = \[\frac{{ - 1}}{3}\]x⁴y⁶z.

Vậy A = \[\frac{{ - 1}}{3}\]x⁴y⁶z.

b) Hệ số của đơn thức A là: \[\frac{{ - 1}}{3}.\]

Bậc của đơn thức A là: 4 + 6 + 1 = 11.

Bài 3: (2,0 điểm)

a) f(x) = 5 + 3x² - x - 2x²

f(x) = (3x² - 2x²) - x + 5

f(x) = x² - x + 5

g(x) = - x² + (3x - x) + 3

g(x) = - x² + 2x + 3

b) h(x) = f(x) + g(x)

h(x) = x² - x + 5 + (-x²) + 2x + 3

h(x) = (x² - x²) + (-x + 2x) + (5 + 3)

h(x) = x + 8

Vậy h(x) = x + 8.

Bài 4: (3,5 điểm)

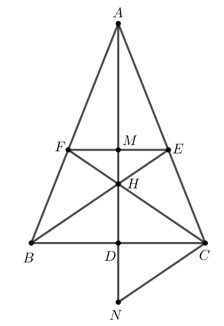
a) Do \[\Delta ABC\] cân tại A nên AB = AC và \[\widehat {ABC} = \widehat {ACB}.\]

Do BE là tia phân giác của \[\widehat {ABC}\] nên \[\widehat {ABE} = \frac{1}{2}\widehat {ABC}.\]

Do CF là tia phân giác của \[\widehat {ACB}\] nên \[\widehat {ACF} = \frac{1}{2}\widehat {ACB}.\]

Do đó \[\widehat {ABE} = \widehat {ACF}.\]

Xét \[\Delta ABE\] và \[\Delta ACF\] có:

\[\widehat A\] chung

AB = AC (chứng minh trên)

\[\widehat {ABE} = \widehat {ACF}\] (chứng minh trên)

\[ \Rightarrow \Delta ABE = \Delta ACF\left( {g - c - g} \right).\]

b) Do hai đường phân giác BE và CF của \[\Delta ABC\] cắt nhau tại H nên AH là đường phân giác của \[\widehat {BAC}\] hay AD là đường phân giác của \[\widehat {BAC}.\]

\[\Delta ABC\] cân tại A có AD là đường phân giác của \[\widehat {BAC}\] nên AD vừa là đường phân giác, vừa là đường trung trực của \[\Delta ABC\].

Do đó D là trung điểm của BC.

Do \[\Delta ABE = \Delta ACF\] nên AE = AF (2 cạnh tương ứng).

\[\Delta AEF\] có AE = AF nên \[\Delta AEF\] cân tại A.

Do đó \[\widehat {AEF} = \widehat {AFE}\].

Xét trong \[\Delta ABC\]: \[\widehat {ABC} + \widehat {ACB} + \widehat {BAC} = 180^\circ \]

Mà \[\widehat {ABC} = \widehat {ACB}\] nên \[2\widehat {ACB} + \widehat {BAC} = 180^\circ \]

\[ \Rightarrow \widehat {ACB} = \frac{{180^\circ  - \widehat {BAC}}}{2}\] (1).

Xét trong \[\Delta AEF\]: \[\widehat {AFE} + \widehat {AEF} + \widehat {EAF} = 180^\circ \]

Mà \[\widehat {AEF} = \widehat {AFE}\] nên \[2\widehat {AEF} + \widehat {EAF} = 180^\circ \]

\[ \Rightarrow \widehat {{\rm{AEF}}} = \frac{{180^\circ  - \widehat {EAF}}}{2}\] (2).

Từ (1) và (2) suy ra \[\widehat {ACB} = \widehat {A{\rm{EF}}}.\]

Mà hai góc này ở vị trí đồng vị nên EF // BC.

c) Gọi M là giao điểm của AH và EF.

Do AH là đường phân giác của \[\widehat {BAC}\] nên AM là đường phân giác của \[\widehat {{\rm{EAF}}}\].

\[\Delta AEF\] cân tại A, có AM là đường phân giác nên AM vừa là đường phân giác, vừa là đường trung trực của \[\Delta AEF\].

Do đó AM là đường trung trực của EF hay AH là đường trung trực của EF.

Do BE là đường phân giác của \[\widehat {ABC}\] nên \[\widehat {HBC} = \frac{1}{2}\widehat {ABC}\].

Do CF là đường phân giác của \[\widehat {ACB}\] nên \[\widehat {HCB} = \frac{1}{2}\widehat {ACB}.\]

Mà \[\widehat {ABC} = \widehat {ACB}\] nên \[\widehat {HBC} = \widehat {HCB}\].

\[\Delta HBC\] có \[\widehat {HBC} = \widehat {HCB}\] nên \[\Delta HBC\] cân tại H.

Do đó HB = HC.

Ta có \[\widehat {BFH}\] là góc ngoài tại đỉnh F của \[\Delta AFC\] nên \[\widehat {BFH} = \widehat {F{\rm{A}}C} + \widehat {FCA}\].

Do đó \[\widehat {BFH} > \widehat {FCA}\].

Do \[\widehat {ABE} = \widehat {ACF}\] nên  \[\widehat {FCA} = \widehat {FBH}\].

Do đó \[\widehat {BFH} > \widehat {FBH}\].

Xét \[\Delta BFH\] có \[\widehat {BFH} > \widehat {FBH}\] nên HB > HF hay HC > HF.

d) Trên tia đối của DH lấy điểm N sao cho DN = DH.

Khi đó HN = HC = 2HD.

Do AD là đường trung trực của BC nên \[A{\rm{D}} \bot {\rm{BC}}{\rm{.}}\]

\[\Delta HCN\] có D là trung điểm của HN mà \[C{\rm{D}} \bot HN\] nên \[\Delta HCN\] cân tại C.

Khi đó HC = CN.

Do đó HN = HC = CN.

\[\Delta HCN\] có HN = HC = CN nên \[\Delta HCN\] đều.

Khi đó \[\widehat {NHC}\] = 60^o.

Xét \[\Delta H{\rm{D}}C\] vuông tại D: \[\widehat {DHC} + \widehat {HC{\rm{D}}} = 90^\circ \] (trong tam giác vuông, hai góc nhọn phụ nhau)

Do đó \[\widehat {HC{\rm{D}}} = 90^\circ  - \widehat {DHC} = 90^\circ  - 60^\circ  = 30^\circ .\]

Mà \[\widehat {HC{\rm{D}}} = \frac{1}{2}\widehat {ACB}\] nên \[\widehat {ACB} = 60^\circ .\]

\[\Delta ABC\] cân tại A có \[\widehat {ACB} = 60^\circ \] nên \[\Delta ABC\] là tam giác đều.

Vậy \[\Delta ABC\] là tam giác đều thì HC = 2HD.

Bài 5: (0,5 điểm)

Thay x = 1 vào f(x) + x.f(-x) = x + 1 ta được:

f(1) + f(-1) = 1 + 1

f(1) + f(-1) = 2

Thay x = -1 vào f(x) + x.f(-x) = x + 1 ta được:

f(-1) + (-1).f(1) = -1 + 1

\[ \Rightarrow \] f(-1) - f(1) = 0.

Do đó f(-1) = f(1).

Mà f(1) + f(-1) = 2 nên 2f(1) = 2 do đó f(1) = 1.

Vậy f(1) = 1.

Bộ 21 Đề thi Toán lớp 7 Học kì 2 năm 2024 có đáp án – Đề 4

Phòng Giáo dục và Đào tạo .....

Đề thi Học kì 2 - Năm học 2024 - 2025

Bài thi môn: Toán lớp 7

Thời gian làm bài: 90 phút

(Đề 4)

 

I. TRẮC NGHIỆM: (5.0 điểm). Chọn một phương án trả lời đúng của mỗi câu hỏi sau rồi ghi vào giấy làm bài.

Câu 1: Biểu thức nào sau đây là đơn thức?

A. x + y.

B. x – y.

C. x.y.

D. \[\frac{x}{y}.\]

Câu 2: Bậc của đơn thức 3x⁴y là

A. 3.

B. 4.

C. 5.

D. 7.

Câu 3: Tam giác ABC vuông tại A có AB = 3cm, BC = 5cm. Độ dài cạnh AC bằng

A. 2cm.

B. 4cm.

C. \[\sqrt {34} \]cm.

D. 8cm.

Câu 4: Tích của hai đơn thức 7x²y và (–xy) bằng

A. –7x3y2.

B. 7x3y2.

C. –7x2y.

D. 6x3y2.

Câu 5: Dựa vào bất đẳng thức tam giác, kiểm tra xem bộ ba nào trong các bộ ba đoạn thẳng có độ dài cho sau đây là ba cạnh của một tam giác?

A. 2cm; 3cm; 6cm.

B. 3cm; 4cm; 6cm.

C. 2cm; 4cm; 6cm.

D. 2cm; 3cm; 5cm.

Câu 6: Đơn thức nào sau đây đồng dạng với đơn thức –3x²y³?

A. –3x3y2.

B. 3(xy)2.

C. –xy3.

D. x2y3.

Câu 7: Tam giác ABC cân tại A có \[\widehat A = 40^\circ \]khi đó số đo của góc B bằng

A. \[100^\circ .\]

B. \[50^\circ .\]

C.\[70^\circ .\]

D. \[40^\circ .\]

Câu 8: Bậc của đa thức 12x⁵y – 2x⁷ + x²y⁶ là

A. 5.

B. 12.

C. 7.

D. 8.

Câu 9: Tam giác ABC có AB < AC < BC. Khẳng định nào sau đây là đúng?

A. \(\widehat C < \widehat B < \widehat A\)

B. \(\widehat B < \widehat C < \widehat A\)

C. \(\widehat A < \widehat C < \widehat B\)

D. \(\widehat A < \widehat B < \widehat C\)

Câu 10: Giá trị của biểu thức 2x² – 5x + 1 tại x = –1 là

A. –2.

B. 8.

C. 0.

D. –6.

Câu 11: Tam giác ABC có BM là đường trung tuyến và G là trọng tâm. Khẳng định nào sau đây là đúng?

A. \[\frac{{BG}}{{BM}} = \frac{3}{2}.\]

B. \[\frac{{BG}}{{GM}} = \frac{1}{2}.\]

C. \[\frac{{MG}}{{BM}} = \frac{1}{3}.\]

D. \[\frac{{BM}}{{BG}} = \frac{2}{3}.\]

Câu 12: Thu gọn đa thức P = – 2x²y – 4xy² + 3x²y + 4xy² được kết quả là

A. P = x2y.

B. P = – 5x2y.

C. P = – x2y.

D. P = x2y – 8xy2.

Câu 13: Tam giác ABC vuông tại A có AB < AC. Vẽ AH vuông góc với BC (H \( \in \) BC). Khẳng định nào sau đây là đúng?

A. HB < HC.

B. HC < HB.

C. AB < AH.

D. AC < AH.

Câu 14: Nghiệm của đa thức f(x) = 2x – 8 là

A. –6.

B. –4.

C. 0.

D. 4.

Câu 15: Cho \[{\rm{\Delta ABC}}\]và \[{\rm{\Delta DEF}}\]có\[\widehat A = \widehat D = 90^\circ \]. Để kết luận \[{\rm{\Delta ABC}}\]=\[{\rm{\Delta DEF}}\] theo trường hợp cạnh huyền – cạnh góc vuông, cần có thêm điều kiện nào sau đây?

A. BC = EF; \(\widehat B = \widehat E\)	C. AB = DE; AC = DF.
B. BC = EF; AC = DF.	D. BC = DE; \(\widehat B = \widehat E\)

 

II. TỰ LUẬN: (5.0 điểm).

Bài 1: (1.25 điểm).

Học sinh lớp 7A góp tiền ủng hộ cho trẻ em khuyết tật. Số tiền đóng góp của mỗi học sinh được ghi ở bảng thống kê sau (đơn vị là nghìn đồng).

5	7	9	5	8	10	5	9	6	10	7	10	6	10	7	6	8	5
6	8	10	5	7	7	10	7	8	5	8	7	8	5	9	7	10	9

 

     a) Dấu hiệu ở đây là gì?

     b) Lập bảng “tần số”;

     c) Tính số trung bình cộng (làm tròn đến chữ số thập phân thứ nhất).

Bài 2: (1.25 điểm).

a)     Cho hai đa thức A(x) = 2x² – x³ + x – 3 và B(x) = x³ – x² + 4 – 3x.

Tính P(x) = A(x) + B(x).

     b) Cho đa thức Q(x)  = 5x² – 5 + a² + ax. Tìm các giá trị của a để Q(x) có nghiệm x = – 1.

Bài 3: (2.5 điểm).

Cho \[{\rm{\Delta ABC}}\]vuông tại A (AB < AC), tia phân giác của góc B cắt AC tại M. Trên tia đối của tia MB lấy điểm D sao cho MB = MD, từ điểm D vẽ đường thẳng vuông góc với AC tại N và cắt BC tại điểm E.

     a) Chứng minh \[{\rm{\Delta ABM  =  \Delta NDM}}\];

     b) Chứng minh BE = DE;

     c) Chứng minh rằng MN < MC.

----------HẾT---------

 

Đáp án và hướng dẫn giải

I. TRẮC NGHIỆM: (5,0 điểm)     

 

Điểm phần trắc nghiệm bằng số câu đúng chia cho 3 (lấy hai chữ số thập phân)

 

Câu	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
Đ/A	C	C	B	A	B	D	C	D	A	B	C	A	A	D	B

                  

Câu 1:

Đơn thức là một biểu thức đại số gồm một số hoặc một biến hoặc một tích giữa các số và các biến.

Do đó, đáp án A, B và D lần lượt chứa các phép toán cộng, trừ, chia nên nó không phải là biểu thức đại số.

Chọn đáp án C

Câu 2:

Số mũ của biến x là 4, số mũ của biến y là 1

Nên bậc của đơn thức 3x⁴y là 4 + 1 = 5.

Chọn đáp án C

Câu 3:

Áp dụng định lý Py-ta-go cho tam giác ABC vuông tại A, ta có:

BC² = AB² + AC² \( \Rightarrow \)AC² = BC² – AB² = 5² – 3² = 16 \( \Rightarrow \) AC = 4cm.

Chọn đáp án B

Câu 4:

Ta có: 7x²y.( –xy) = –7.(x².x).(y.y) = –7x³y²

Chọn đáp án A

Câu 5:

+ Ta có: 2 + 3 = 5 < 6 nên bộ ba số 2cm; 3cm; 6cm không phải là ba cạnh của tam giác.

+ Có: 3 + 4 = 7 > 6; 3 + 6 = 9 > 4 ; 6 + 4 = 10 > 3 nên bộ ba số 3cm; 4cm; 6cm là độ dài ba cạnh của tam giác.

+ Ta có: 2 + 4 = 6 nên bộ ba số 2cm; 4cm; 6cm không phải là độ dài ba cạnh của tam giác.

+ Lại có: 2 + 3 = 5 nên bộ ba số 2cm; 3cm; 5cm không phải là độ dài ba cạnh của tam giác.

Chọn đáp án B

Câu 6:

Hai đơn thức đồng dạng là hai đơn thức có hệ số khác 0 và có cùng phần biến.

Do đó đơn thức đồng dạng với đơn thức –3x²y³ là x²y³.

Chọn đáp án D

Câu 7:

Tam giác ABC cân tại A nên \(\widehat B = \frac{{180^\circ  - \widehat A}}{2} = \frac{{180^\circ  - 40^\circ }}{2} = 70^\circ \).

Chọn đáp án C

Câu 8:

Ta có: 12x⁵y – 2x⁷ + x²y⁶

Hạng tử 12x⁵y có bậc là 5 + 1 = 6

Hạng tử –2x⁷ có bậc là 7

Hạng tử x²y⁶ có bậc là 2 + 6 = 8 (cao nhất)

Do đó bậc của đa thức 12x⁵y – 2x⁷ + x²y⁶ là 8.

Chọn đáp án D

Câu 9:

Vì AB < AC < BC nên\(\widehat C < \widehat B < \widehat A\)  (Trong một tam giác, góc đối diện với cạnh lớn hơn thì lớn hơn).

Chọn đáp án A

Câu 10:

Thay x = –1 vào biểu thức 2x² – 5x + 1 ta được:

2.( –1)² – 5.( –1) + 1 = 2 + 5 + 1 = 8

Chọn đáp án B

Câu 11:

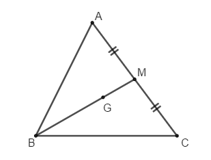
G là trọng tâm của tam giác ABC có BM là trung tuyến nên

\(\frac{{BG}}{{BM}} = \frac{2}{3}\); \(\frac{{BG}}{{GM}} = 2\); \(\frac{{MG}}{{BM}} = \frac{1}{3}\); \(\frac{{BM}}{{BG}} = \frac{3}{2}\)

Chọn đáp án C

Câu 12:

P = – 2x²y – 4xy² + 3x²y + 4xy²

= (–2x²y + 3x²y) + (–4xy² + 4xy²)

= x²y + 0 = x²y

Vậy P = x²y.

Chọn đáp án A

Câu 13:

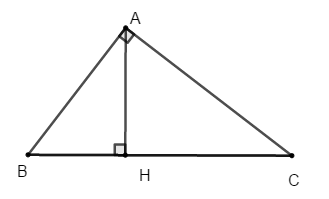
+ Vì AB < AC nên HB < HC (quan hệ đường xiên và hình chiếu) nên đáp án A đúng, đáp án B sai.

+ Tam giác ABH và ACH đều vuông tại H nên AB > AH và AC > AH (trong tam giác vuông, cạnh huyền là cạnh lớn nhất).

Chọn đáp án A

Câu 14:

Ta có: f(x) = 0 hay 2x – 8 = 0 \( \Rightarrow \) x = 8 : 2 = 4

Vậy x = 4 là nghiệm của đa thức f(x).

Chọn đáp án D

Câu 15:

Ta có:  \[{\rm{\Delta ABC}}\]và \[{\rm{\Delta DEF}}\]có\[\widehat A = \widehat D = 90^\circ \].

Để kết luận \[{\rm{\Delta ABC}}\]=\[{\rm{\Delta DEF}}\] theo trường hợp cạnh huyền – cạnh góc vuông, cần có thêm hai điều kiện:

1. BC = EF (hai cạnh huyền bằng nhau)

2. AC = DF hoặc AB = DE (hai cạnh góc vuông tương ứng bằng nhau)

Chọn đáp án B

 

II. TỰ LUẬN: (5,0 điểm)

Bài 1.

a) Dấu hiệu là: Số tiền đóng góp của mỗi học sinh lớp 7A.  (0,25 điểm)

b) Bảng “tần số” (0,5 điểm)

Giá trị (x)	5	6	7	8	9	10
Tần số (n)	7	4	8	6	4	7	N = 36

c) Số trung bình cộng

\(\overline X  = \frac{{5.7 + 6.4 + 7.8 + 8.6 + 9.4 + 10.7}}{{36}} = \frac{{269}}{{36}} \approx 7,5\).    (0,5 điểm)

Bài 2.

a) A(x) = 2x² – x³ + x – 3

B(x) = x³ – x² + 4 – 3x

Cách 1. Ta có: P(x) = A(x) + B(x)

= (2x² – x³ + x – 3) + (x³ – x² + 4 – 3x)            (0,25 điểm)

= (2x² – x²) + (– x³ + x³) + (x – 3x) + (–3 + 4)     (0,25 điểm)

= x² – 2x + 1                              (0,25 điểm)

Cách 2:         A(x) = – x³ + 2x² + x  – 3

                       B(x) =    x³ – x²  – 3x + 4    (0,25 điểm) 

P(x) = A(x) + B(x) =           x² – 2x + 1        (0,5 điểm)

b) Q(x) có nghiệm x = – 1

\( \Rightarrow \) Q(– 1) = 5.(– 1)² – 5 + a² + a.(–1) = 0     (0,25 điểm)

\( \Rightarrow \) a² – a = 0

\( \Rightarrow \) a(a – 1) =0

\( \Rightarrow \) a = 0 hoặc a = 1

Vậy a = 0; a = 1 thì thỏa mãn yêu cầu bài toán.  (0,25 điểm)

Bài 3.

Vẽ hình đúng, ghi GT, KL được 0,5 điểm.

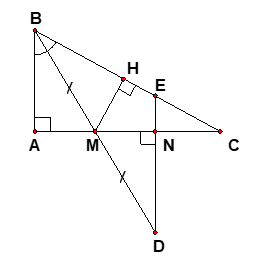
a) Xét \[{\rm{\Delta ABM}}\] và \[{\rm{\Delta NDM}}\]có:

  \(\widehat A = \widehat N = 90^\circ \)(gt)

  MB = MD (gt)

  \(\widehat {AMB} = \widehat {NMD}\)  (đối đỉnh)

Do đó \[{\rm{\Delta ABM  =  \Delta NDM}}\](cạnh huyền – góc nhọn) (đpcm)    (0,75 điểm)

b)Ta có: \(\widehat {ABM} = \widehat {NDM}\) (vì \[{\rm{\Delta ABM  =  \Delta NDM}}\])

\(\widehat {ABM} = \widehat {CBM}\) (vì BM là phân giác của góc ABC)

Do đó: \(\widehat {NDM} = \widehat {CBM}\) hay \(\widehat {EDB} = \widehat {EBD}\)\( \Rightarrow \)\[{\rm{\Delta BED}}\] cân tại E           (0,5 điểm)

Suy ra: BE = DE (đpcm)               (0,25 điểm)

c) Kẻ MH vuông góc với BC tại H

Ta có: MH = MA (vì BM là tia phân giác của góc ABC)

      và MA = MN (vì \[{\rm{\Delta ABM  =  \Delta NDM}}\])

Do đó: MN = MH             (0,25 điểm)

Xét tam giác MHC vuông tại H có MH < MC (vì MC là cạnh huyền)

Vậy MN < MC (đpcm)                  (0,25 điểm)

 

-----------------------

 

Bộ 21 Đề thi Toán lớp 7 Học kì 2 năm 2024 có đáp án – Đề 5

Phòng Giáo dục và Đào tạo .....

Đề thi Học kì 2 - Năm học 2024 - 2025

Bài thi môn: Toán lớp 7

Thời gian làm bài: 90 phút

(Đề 5)

I. Trắc nghiệm (3,0 điểm) Khoanh tròn vào chữ cái đứng trước câu trả lời đúng

Câu 1. Tích của hai đơn thức \[ - \frac{1}{2}\]x²y² và 6xy³ là:

A. 3x³y⁶.

B. -3x³y⁵.

C. 3x²y⁶.

D. \[\frac{{ - 1}}{3}\]x²y⁶.

Câu 2. Hệ số cao nhất của đa thức P(x) = 2x³ + x⁴ - 8x² + 20 là:

A. 1.

B. 2.

C. -8.

D. 20.

Câu 3. Giá trị của đa thức P = x²y + 2xy + 3 tại x = -1, y = 2 là:

A. 8.

B. 1.

C. 5.

D. -1.

Câu 4. Cho tam giác ABC có \[\widehat B\] tù, \[\widehat A > \widehat C.\] Khẳng định nào sau đây là đúng?

A. AC > BC > AB.

B. BC > AB > AC.

C. AB > AC > BC.

D. AC > AB > BC.

Câu 5. Cho hai đa thức P(x) = -x³ + 2x² + x - 1 và Q(x) = x³ - x² - x + 2. Nghiệm của đa thức P(x) + Q(x) là:

A. Vô nghiệm.

B. -1.

C. 1.

D. 0.

Câu 6. Bậc của đa thức A = x²y⁴ - x²y⁵ - 8x⁶ + 2021¹⁸ là :

A. 6.

B. 18.

C. 7.

D. 2021.

II. Tự luận (7,0 điểm)

Bài 1. (2 điểm) Cho hai đa thức :

f(x) = -6x³ - x⁴ + 3x² + 2x⁴ - x - x² + 1 và g(x) = 2x³ - x + x² + x³.

a) Thu gọn và sắp xếp các hạng tử của 2 đa thức theo lũy thừa giảm dần của biến.

b) Tìm bậc, hệ số cao nhất, hệ số tự do của f(x) và g(x).

c) Tính h(x) = g(x) - f(x) và h(-1).

Bài 2. (1,5 điểm) Tìm nghiệm của các đa thức sau:

a) M = 2x - \[\frac{1}{2}.\]

b) N = (x + 5)(4x² - 1).

c) P = 9x³ - 25x.

Bài 3. (3,0 điểm) Cho tam giác ABC vuông tại A, AB = 9 cm, BC = 15 cm. Trên tia đối của tia AB lấy điểm E sao cho A là trung điểm của BE.

a) Chứng minh rằng \[\Delta ABC = \Delta A{\rm{E}}C.\]

b) Vẽ đường trung tuyến BH của \[\Delta BEC\] cắt cạnh AC tại M. Chứng minh M là trọng tâm của \[\Delta BEC\] và tính độ dài đoạn CM.

c) Từ A vẽ đường thẳng song song với EC, đường thẳng này cắt cạnh BC tại K. Chứng minh rằng ba điểm E, M, K thẳng hàng.

Bài 4. (0,5 điểm) Cho ba số thực x, y, z thỏa mãn x(x² + y) - yz = 0.

Biết rằng trong ba số đó có một số bằng 0, một số âm, một số dương. Hãy chỉ rõ số nào bằng 0, số nào âm, số nào dương.

 

Đáp án và hướng dẫn giải

I. Trắc nghiệm (3,0 điểm) Khoanh tròn trước chữ cái đứng trước câu trả lời đúng

Câu 1. Tích của hai đơn thức \[ - \frac{1}{2}\]x²y² và 6xy³ là:

A. 3x³y⁶.

B. -3x³y⁵.

C. 3x²y⁶.

D. \[\frac{{ - 1}}{3}\]x²y⁶.

Hướng dẫn giải

Đáp án đúng là: B

Ta có \[\left( { - \frac{1}{2}{x^2}{y^2}} \right)\].6xy³ = \[\left( { - \frac{1}{2}.6} \right)\].(x².x).(y².y³) = -3x³y⁵.

Chọn đáp án B.

Câu 2. Hệ số cao nhất của đa thức P(x) = 2x³ + x⁴ - 8x² + 20 là:

A. 1.

B. 2.

C. -8.

D. 20.

Hướng dẫn giải

Đáp án đúng là: B

Hệ số cao nhất của đa thức P(x) là hệ số của hạng tử 2x³ bằng 2.

Chọn đáp án B.

Câu 3. Giá trị của đa thức P = x²y + 2xy + 3 tại x = -1, y = 2 là:

A. 8.

B. 1.

C. 5.

D. -1.

Hướng dẫn giải

Đáp án đúng là: B

Thay x = -1, y = 2 vào đa thức P ta có:

P = (-1)².2 + 2.(-1).2 + 3 = 1.2 + (-2).2 + 3 = 2 - 4 + 3 = 1.

Chọn đáp án B.

Câu 4. Cho tam giác ABC có \[\widehat B\] tù, \[\widehat A > \widehat C.\] Khẳng định nào sau đây là đúng?

A. AC > BC > AB.

B. BC > AB > AC.

C. AB > AC > BC.

D. AC > AB > BC.

Hướng dẫn giải

Đáp án đúng là: A

Do \[\widehat B\] tù nên \[\widehat B\] là góc lớn nhất trong tam giác ABC.

Lại có \[\widehat A > \widehat C\] nên \[\widehat B > \widehat A > \widehat C\].

Cạnh đối diện với \[\widehat B\] là AC, cạnh đối diện với \[\widehat A\] là BC, cạnh đối diện với \[\widehat C\] là AB.

Trong một tam giác, cạnh đối diện với góc lớn hơn thì lớn hơn nên \[\widehat B > \widehat A > \widehat C\] thì

AC > BC > AB.

Chọn đáp án A.

Câu 5. Cho hai đa thức P(x) = -x³ + 2x² + x - 1 và Q(x) = x³ - x² - x + 2. Nghiệm của đa thức P(x) + Q(x) là:

A. Vô nghiệm.

B. -1.

C. 1.

D. 0.

Hướng dẫn giải

Đáp án đúng là: A

Ta có P(x) + Q(x) = -x³ + 2x² + x - 1 + x³ - x² - x + 2

P(x) + Q(x) = (-x³ + x³) + (2x² - x²) + (x - x) + (-1 + 2)

P(x) + Q(x) = x² + 1.

Ta có x² ≥ 0 với mọi x nên x² + 1 > 0 với mọi x.

Do đó không có giá trị của x thỏa mãn x² + 1 = 0.

Khi đó đa thức P(x) + Q(x) vô nghiệm.

Chọn đáp án A.

Câu 6. Bậc của đa thức A = x²y⁴ - x²y⁵ - 8x⁶ + 2021¹⁸ là:

A. 6.

B. 18.

C. 7.

D. 2021.

Hướng dẫn giải

Đáp án đúng là: C

Bậc của đa thức A là bậc của hạng tử - x²y⁵.

Bậc của hạng tử - x²y⁵ là 7 nên chọn đáp án C.

II. Tự luận (7,0 điểm)

Bài 1. (2 điểm)

a) f(x) = -6x³ - x⁴ + 3x² + 2x⁴ - x - x² + 1

f(x) = (-x⁴ + 2x⁴) - 6x³ + (3x² - x²) - x + 1

f(x) = x⁴ - 6x³ + 2x² - x + 1

 g(x) = 2x³ - x + x² + x³

g(x) = (2x³ + x³) + x² - x

g(x) = 3x³ + x² - x

b) Bậc của f(x): 4

Hệ số cao nhất của f(x): 1

Hệ số tự do của f(x): 1

Bậc của g(x): 3

Hệ số cao nhất của g(x): 3

Hệ số tự do của g(x): 0

c) h(x) = g(x) - f(x)

h(x) = 3x³ + x² - x - (x⁴ - 6x³ + 2x² - x + 1)

h(x) = 3x³ + x² - x - x⁴ + 6x³ - 2x² + x - 1

h(x) = -x⁴ + (3x³ + 6x³) + (x² - 2x²) + (-x + x) - 1

h(x) = -x⁴ + 9x³ - x² - 1

Khi đó h(-1) = -[(-1)]⁴ + 9.(-1)³ - (-1)² - 1 = -1 + (-9) - 1 - 1 = -12.

Bài 2. (1,5 điểm)

a) M = 2x - \[\frac{1}{2}.\]

b) N = (x + 5)(4x² - 1).

c) P = 9x³ - 25x.

a) Để M = 0 thì 2x - \[\frac{1}{2}\] = 0

\[ \Rightarrow \] 2x = \[\frac{1}{2}\]

\[ \Rightarrow \] x = \[\frac{1}{2}:2\]

\[ \Rightarrow \] x = \[\frac{1}{2}.\frac{1}{2}\]

\[ \Rightarrow \] x = \[\frac{1}{4}\]

Vậy x = \[\frac{1}{4}\].

b) Để N = 0 thì (x + 5)(4x² - 1) = 0

Trường hợp 1.

x + 5 = 0

\[ \Rightarrow \] x = -5

Trường hợp 2. 4x² - 1 = 0

\[ \Rightarrow \] 4x² = 1

\[ \Rightarrow \] x² = \[\frac{1}{4}\]

+) x² = \[{\left( {\frac{1}{2}} \right)^2}\] \[ \Rightarrow \] x = \[\frac{1}{2}\]

+) x² = \[{\left( {\frac{{ - 1}}{2}} \right)^2}\] \[ \Rightarrow \] x = \[\frac{{ - 1}}{2}\]

Vậy x = -5 hoặc x = \[\frac{{ - 1}}{2}\] hoặc x = \[\frac{1}{2}.\]

Bài 3. (3,0 điểm)

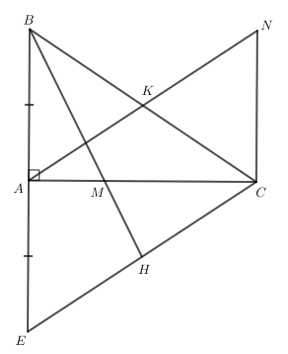
a) Xét \[\Delta ABC\] vuông tại A và \[\Delta AEC\] vuông tại A có:

AB = AE (theo giả thiết)

AC chung

\[ \Rightarrow \Delta ABC = \Delta A{\rm{E}}C\] (2 cạnh góc vuông)

b) Do A là trung điểm của BE nên CA là đường trung tuyến ứng của \[\Delta BEC.\]

Xét \[\Delta BEC\] có CA và BH là hai đường trung tuyến cắt nhau tại M.

Do đó M là trọng tâm của \[\Delta BEC.\]

Do đó CM = \[\frac{2}{3}\]CA.

 Áp dụng định lý Pytago vào \[\Delta ABC\] vuông tại A:

AB² + AC² = BC²

\[ \Rightarrow \] 9² + AC² = 15²

\[ \Rightarrow \] AC² = 225 - 81

\[ \Rightarrow \] AC² = 144

\[ \Rightarrow \] AC = 12 cm

Khi đó CM = \[\frac{2}{3}\]CA = \[\frac{2}{3}\].12 = 8 cm.

Vậy CM = 8 cm.

c) Trên tia đối của tia KA lấy điểm N sao cho KN = KA.

Do \[\Delta ABC = \Delta A{\rm{E}}C\] (2 cạnh góc vuông) nên BC = EC (2 cạnh tương ứng) và \[\widehat {ACB} = \widehat {AC{\rm{E}}}\] (2 góc tương ứng).

\[ \Rightarrow \widehat {KCA} = \widehat {ACE}\].

Do AK // EC nên \[\widehat {K{\rm{A}}C} = \widehat {AC{\rm{E}}}\] (2 góc so le trong)

Do đó \[\widehat {KCA} = \widehat {K{\rm{A}}C}\].

\[\Delta K{\rm{A}}C\] có \[\widehat {KCA} = \widehat {K{\rm{A}}C}\] nên \[\Delta K{\rm{A}}C\] cân tại K.

Do đó KA = KC.

Mà KA = KN = \[\frac{1}{2}\] AN nên KA = KN = KC = \[\frac{1}{2}\] AN.

\[\Delta ACN\] có KA = KN = KC = \[\frac{1}{2}\] AN nên \[\Delta ACN\] vuông tại C.

Xét \[\Delta ACN\] vuông tại C và \[\Delta CA{\rm{E}}\] vuông tại A:

\[\widehat {NAC} = \widehat {EC{\rm{A}}}\] (chứng minh trên).

AC chung.

\[ \Rightarrow \Delta ACN = \Delta CA{\rm{E}}\] (góc nhọn - cạnh góc vuông).

\[ \Rightarrow \] AN = CE (2 cạnh tương ứng).

Mà EC = BC nên AN = BC.

Mà AN = 2AK nên BC = 2AK.

Lại có AK = KC nên BC = 2KC.

Do đó K là trung điểm của BC.

\[\Delta BEC\] có M là trọng tâm, lại có K là trung điểm của BC nên E, M, K thẳng hàng.

Vậy E, M, K thẳng hàng.

Bài 4. (0,5 điểm)

Nếu x = 0 thì 0.(0² + y) - yz = 0

\[ \Rightarrow \] -yz = 0.

Khi đó y = 0 hoặc z = 0 (vô lí do chỉ có 1 số bằng 0).

Do đó x ≠ 0.

Nếu y = 0 thì x.(x² + 0) - 0.z = 0

\[ \Rightarrow \] x³ = 0.

Khi đó x = 0 (vô lí do chỉ có 1 số bằng 0).

Do đó y ≠ 0.

Do đó z = 0.

Khi đó x.(x² + y) - yz = x.(x² + y) - y.0 = x.(x² + y) = 0.

Do x ≠ 0 nên x² + y = 0.

\[ \Rightarrow \] x² = -y.

Do x ≠ 0 nên x² > 0 khi đó -y > 0 do đó y < 0.

Vậy x là số dương, y là số âm, z bằng 0.

 

Bộ 21 Đề thi Toán lớp 7 Học kì 2 năm 2024 có đáp án – Đề 6

Phòng Giáo dục và Đào tạo .....

Đề thi Học kì 2 - Năm học 2024 - 2025

Bài thi môn: Toán lớp 7

Thời gian làm bài: 90 phút

(Đề 6)

I.TRẮC NGHIỆM: (3 điểm)

Câu 1: Ba độ dài nào dưới đây là  độ dài ba cạnh của một tam giác:

A. 2cm, 4cm, 6cm           

B. 2cm, 4cm, 7cm    

C. 3cm, 4cm, 5cm             

D. 2cm, 3cm, 5cm

Câu 2: Đơn thức nào đồng dạng với đơn thức \(2{x^2}y\):

A. \(x{y^2}\)            B. \(2x{y^2}\)  

C. \( - 5{x^2}y\)       D. \(2xy\)

Câu 3: \(\Delta ABC\) có \[\widehat {\rm{A}}{\rm{ = 9}}{{\rm{0}}^{\rm{0}}}{\rm{, }}\widehat B{\rm{ = 3}}{{\rm{0}}^{\rm{0}}}{\rm{\;}}\]thì quan hệ giữa ba cạnh AB, AC, BC là:

A. BC  > AB  > AC         

B. AC  > AB  >  BC 

C. AB > AC > BC             

D. BC > AC > AB

Câu 4: Biểu thức :  \({x^2} + 2x\), tại x = –1 có giá trị là:

A. –3                        B. –1     

C. 3                          D. 0

Câu 5: Với x = – 1 là nghiệm của đa thức nào sau đây:                       

A. x + 1                    B. X – 1   

C. 2x + \(\frac{1}{2}\)  D. X² + 1

Câu 6: Tam giác ABC có G là trọng tâm, AM là đường trung tuyến, ta có:

A. AG =\(\frac{1}{2}\)AM        

B. AG =\(\frac{1}{3}\)AM  

C. AG =\(\frac{3}{2}\)AM.  

D. AG =\(\frac{2}{3}\)AM

Câu 7: Đơn thức \(\frac{{ - 1}}{2}{x^2}{y^5}{z^3}\) có bậc:

A. 3                          B. 5   

C. 2                          D. 10

Câu 8: Cho \(P = 3{x^2}y - 5{x^2}y + 7{x^2}y\), kết quả rút gọn P là:

A. \({x^2}y\)            B. \(15{x^2}y\)

C. \[5{x^2}y\]          D. \(5{x^6}{y^3}\)

Câu 9 : Cho hai đa thức : \[A = 2{x^2} + x--1\] ;  \[B = x--1.\] Kết quả A – B  là :

A. \[2{x^2} + 2x + 2\;\;\;\;\;\;\;\;\;\;\;\;\]

B. \[2{x^2} + 2x\;\;\;\;\;\;\;\;\;\;\;\;\]

C. \[2{x^2}\]        

D. \[2{x^2}--2\]

Câu 10: Gọi M là trung điểm của BC trong tam giác ABC. AM gọi là đường gì của tam giác ABC ?

A. Đường cao.             

 B. Đường phân giác.

C. Đường trung tuyến.         

D. Đường trung trực

Câu 11: Cho hình vẽ bên. So sánh AB, BC, BD ta được:

A. AB < BC < BD     

B. AB > BC > BD    

C. BC  > BD > AB     

D. BD < BC < AB

Câu 12: Cho \[A\left( x \right) = 2{x^2} + x--1\;;{\rm{   }}B\left( x \right) = x--1\]. Tại\[x = 1\], đa thức A(x) – B(x) có giá trị là:

A. 2                          B. 0    

C. –1                        D. 1

II. TỰ LUẬN (7 điểm)

Bài 1: (1.5 điểm) Một giáo viên theo dõi thời gian giải bài toán (tính theo phút) của một lớp học và ghi lại:   

10	5	4	7	7	7	4	7	9	10
6	8	6	10	8	9	6	8	7	7
9	7	8	8	6	8	6	6	8	7

a) Dấu hiệu cần tìm hiểu ở đây là gì?

b) Lập bảng tần số và  tìm Mốt của dấu hiệu;

c)  Tính thời gian trung bình của lớp.

Bài 2: (1.0 điểm) Thu gọn các đơn thức:

\(a{\rm{)  }}2{x^2}{y^2}.\frac{1}{4}x{y^3}.( - 3xy){\rm{         ;   b)    (}}--{\rm{2}}{{\rm{x}}^3}y{)^2}.x{y^2}.\frac{1}{2}{y^5}\)

Bài 3: (1.5 điểm) Cho hai đa thức:

                                                             \[\begin{array}{*{20}{l}}{P\left( x \right){\rm{ }} = {\rm{ }}2{x^3} - {\rm{ }}2x{\rm{ }} + {\rm{ }}{x^2} + 3x{\rm{ }} + 2{\rm{ }}.}\\{\;Q\left( x \right){\rm{ }} = {\rm{ }}4{x^3} - {\rm{ }}3{x^2} - {\rm{ }}3x{\rm{ }} + {\rm{ }}4x{\rm{ }} - 3{x^3} + {\rm{ }}4{x^2} + 1{\rm{ }}.}\end{array}\]                         

a) Rút gọn P(x), Q(x);

b) Chứng tỏ x = –1  là nghiệm của P(x), Q(x);

Bài 4: (2.5 điểm) Cho tam giác ABC. Ở phía ngoài tam giác đó vẽ các tam giác vuông cân tại A là ABD và ACE.

a) Chứng minh CD = BE và CD vuông góc với BE;

b) Lấy điểm K nằm trong tam giác ABD sao cho góc ABK bằng 30⁰, BA = BK. Chứng minh: AK = KD.

Bài 5: (0.5 điểm) Tìm  x, y thỏa mãn : \[{x^2} + 2{x^2}{y^2} + 2{y^2}\; - \left( {{x^2}{y^2} + 2{x^2}} \right)\; - 2 = 0\].

---------------HẾT--------------

Đáp án và hướng dẫn giải

I. Trắc nghiệm

Mỗi câu đúng được 0,25 điểm 

 

Câu 1:

+ Ta có: 2 + 4 = 6 nên bộ ba số 2cm, 4cm, 6cm không phải là độ dài ba cạnh của một tam giác.

+ Có 2 + 4 = 6 < 7 nên bộ ba số 2cm, 4cm, 7cm không phải độ dài ba cạnh của tam giác.

+ Ta có: 3 + 4 = 7 > 5; 3 + 5 = 8 > 4 và 4 + 5 = 9 > 3 nên bộ ba số 3cm, 4cm, 5 cm là độ dài ba cạnh của một tam giác.

+ Vì 2 + 3 = 5 nên bộ ba số 2cm, 3cm, 5 cm không phải độ dài ba cạnh của một tam giác.

Chọn đáp án C

Câu 2:

Hai đơn thức đồng dạng là hai đơn thức có hệ số khác 0 và có cùng phần biến.

Do đó: đơn thức đồng dạng với đơn thức 2x²y là –5x²y.

Chọn đáp án C

Câu 3:

Ta có: \(\widehat A + \widehat B + \widehat C = 180^\circ \)\( \Rightarrow \widehat C = 180^\circ  - \widehat A - \widehat B = 180^\circ  - 90^\circ  - 30^\circ  = 60^\circ \)

Vì \(90^\circ  > 60^\circ  > 30^\circ \) nên \(\widehat A > \widehat C > \widehat B\)

Do đó: BC > AB > AC (trong một tam giác, cạnh đối diện với góc lớn hơn thì lớn hơn).

Chọn đáp án A

Câu 4:

Thay x = –1 vào biểu thức x² + 2x ta được:

(–1)² + 2.( –1) = 1 – 2 = –1

Chọn đáp án B

Câu 5:

+) Thay x = –1 vào đa thức x + 1 ta được: –1 + 1 = 0 nên x = –1 là nghiệm của đa thức x + 1, đáp án A đúng.

+) Thay x = –1 vào đa thức x – 1 ta được: –1 – 1 = –2 \( \ne \)0 nên x = –1 không là nghiệm của đa thức x – 1, B sai.

+) Thay x = –1 vào đa thức 2x + \(\frac{1}{2}\), ta được: 2.( –1) + \(\frac{1}{2}\) = \(\frac{{ - 3}}{2} \ne 0\) nên x = –1 không phải là nghiệm của đa thức 2x + \(\frac{1}{2}\), C sai.

+) Thay x = –1 vào đa thức x² +1 ta được: (–1)² + 1 = 2 \( \ne \)0 nên x = –1 không phải là nghiệm của đa thức x² + 1, D sai.

Chọn đáp án A

Câu 6:

Tam giác ABC có AM là trung tuyến, G là trọng tâm

Nên theo tính chất trọng tâm ta có: AG =\(\frac{2}{3}\)AM

Chọn đáp án D

Câu 7:

Đơn thức \(\frac{{ - 1}}{2}{x^2}{y^5}{z^3}\) có bậc là 2 + 5 + 3 = 10.

Chọn đáp án D

Câu 8:

Ta có: \(P = 3{x^2}y - 5{x^2}y + 7{x^2}y\)\( = \left( {3 - 5 + 7} \right){x^2}y = 5{x^2}y\).

Chọn đáp án C

Câu 9:

Ta có: A – B = (2x² + x – 1) – (x – 1) = 2x² + x – 1 – x + 1 = 2x²

Chọn đáp án C

Câu 10:

M là trung điểm của BC trong tam giác ABC nên AM là đường trung tuyến của tam giác ABC.

Chọn đáp án C

Câu 11:

Vì BA \( \bot \) AD và C nằm giữa A và D nên AC < AD

Do đó: AB < BC < BD (quan hệ đường xiên và hình chiếu).

Chọn đáp án A

Câu 12:

Ta có: A(x) – B(x) = (2x² + x – 1) – (x – 1) = 2x²

Thay x = 1 vào biểu thức 2x² ta được: 2.1² = 2

Vậy giá trị của biểu thức A(x) – B(x) tại x = 1 là 2.

Chọn đáp án A

II. Tự luận

Bài 1:

a) Dấu hiệu ở đây là thời gian giải bài toán của mỗi học sinh trong lớp. (0,25 điểm)

b) Bảng tần số (0,75 điểm)

Giá trị	4	5	6	7	8	9	10
Tần số	2	1	6	8	7	3	3	N = 30

 

Mốt của dấu hiệu là 7. (0,25 điểm)

c)  Số trung bình cộng là

 \(\overline X  = \frac{{4.2 + 5.1 + 6.6 + 7.8 + 8.7 + 9.3 + 10.3}}{{30}} = \frac{{218}}{{30}} \approx 7,3\)   (0,25 điểm)

Bài 2:

a) \(2{x^2}{y^2}.\frac{1}{4}x{y^3}.( - 3xy){\rm{         }}\)

\( = \left( {2.\frac{1}{4}.\left( { - 3} \right)} \right).\left( {{x^2}.x.x} \right).\left( {{y^2}.{y^3}.y} \right)\) \({\rm{ =  }}\frac{{ - 3}}{2}{{\rm{x}}^4}{{\rm{y}}^6}\)      (0,5 điểm)

b) \({{\rm{(}}--{\rm{2}}{{\rm{x}}^3}y)^2}.x{y^2}.\frac{1}{2}{y^5}\)

\( = 4{x^6}{y^2}.x{y^2}.\frac{1}{2}{y^5}\)

\( = \left( {4.\frac{1}{2}} \right).\left( {{x^6}.x} \right).\left( {{y^2}.{y^2}.{y^5}} \right)\)

\({\rm{ =   2}}{{\rm{x}}^7}{y^9}\)              (0,5 điểm)

Bài 3:

a)   P(x) = 2x³ – 2x + x² + 3x + 2 = 2x³ + x² + (–2x + 3x) + 2 = 2x³ + x² + x + 2    (0,25 điểm)

      Q(x) = 4x³ – 3x² – 3x + 4x – 3x³ + 4x² +1 

               = (4x³ – 3x³) + (–3x² + 4x²) + (–3x + 4x) + 1

               = x³ + x²  + x + 1                     (0,25 điểm)

b) x =  –1 là nghiệm của  P(x) vì:

  P(–1) =  2.(–1)³ + (–1)²  + (–1) + 2 =  – 2 + 1 – 1 + 2 = 0 .    (0,5 điểm)

      x =  –1 là nghiệm của  Q(x) vì:

  Q(–1) =  (–1)³ + (–1)² + (–1) + 1 =  –1 + 1 – 1 + 1 = 0 .          (0,5 điểm)

Bài 4:

-Vẽ hình đúng được 0,5 điểm. (sai hình không chấm)

a) Xét tam giác ADC và tam giác ABE có:

 AD = AB (Tam giác ADB cân tại A)

 \[\widehat {DAC} = \widehat {BAE}( = {90^0} + \widehat {BAC})\]

 AC = AE (Tam giác ACE vuông tại A)  

Do đó: \[\Delta ADC = \Delta ABE(c.g.c)\]

Suy ra DC = BE (2 cạnh tương ứng); \[\widehat {ADC} = \widehat {ABE}\](2 góc tương ứng)

Gọi I là giao điểm của DC và AB.

Ta có: \[\widehat {DIA} = \widehat {BIC}\] (đối đỉnh); \[\widehat {ADC} = \widehat {ABE}\] (c/m trên)

Mà \[\widehat {DIA} + \widehat {ADC} = {90^0}\](tam giác IAD vuông tại A) suy ra \[\widehat {BIC} + \widehat {ABE} = {90^0}\]

Suy ra DC vuông góc với BE.    (1 điểm)

b)

Vẽ tam giác đều BPD sao cho P và A nằm cùng phía đối với BD

\[\Delta APB = \Delta APD(c.c.c) \Rightarrow \widehat {APB} = \widehat {APD} = {30^0}\]

Ta có: \[\widehat {ABP} = \widehat {DBK} = {45^0} - {30^0} = {15^0}\] suy ra \[\Delta KDB = \Delta APB(c.g.c)\]

Suy ra  \[\widehat {KDB} = \widehat {APB} = {30^0}\] suy ra \[\widehat {ADK} = {15^0}\](1)                                                           

Tam giác BAK cân tại B có góc ABK = 30⁰

Nên \[\widehat {BAK} = \frac{{{{180}^0} - {{30}^0}}}{2} = {75^0}\]suy ra \[\widehat {KAD} = {90^0} - {75^0} = {15^0}\](2)

Từ (1) và (2) suy ra: \(\widehat {ADK} = \widehat {KAD}\) nên tam giác KDA cân tại K suy ra KA = KD (1 điểm)

Bài 5:

Ta có: \[{x^2} + 2{x^2}{y^2} + 2{y^2}\; - \left( {{x^2}{y^2} + 2{x^2}} \right)\; - 2 = 0\]

\( \Leftrightarrow \) x²y² – x² + 2y² – 2 = 0

\( \Leftrightarrow \) x²(y² – 1) + 2(y² – 1) = 0

\( \Leftrightarrow \) (y² – 1).( x²  + 2) = 0                           (0,25 điểm)

Vì x² + 2 > 0 với mọi x

Do đó y² – 1 = 0 \( \Rightarrow y\) = 1 hoặc y = –1

Vậy y \( \in \){1; – 1} và x là một số thực tùy ý.    (0,25 điểm)

 

-----------------------

Bộ 21 Đề thi Toán lớp 7 Học kì 2 năm 2024 có đáp án – Đề 7

Phòng Giáo dục và Đào tạo .....

Đề thi Học kì 2 - Năm học 2024 - 2025

Bài thi môn: Toán lớp 7

Thời gian làm bài: 90 phút

(Đề 7)

I. Trắc nghiệm (2,0 điểm) Khoanh tròn vào chữ cái đứng trước câu trả lời đúng

Câu 1. Bậc của đơn thức 2²x³y là :

A. 6. 

B. 5.

C. 3.

D. 4.

Câu 2. Cho \[\Delta ABC\] biết BC = 4 cm, AB = 5 cm, AC = 3 cm. Khi đó ta có tam giác ABC :

A. nhọn.

B. vuông tại A.

C. vuông tại B.

D. vuông tại C.

Câu 3. Giá trị có tần số lớn nhất được gọi là :

A. tần số của giá trị đó.

B. mốt của dấu hiệu.

C. số trung bình cộng của dấu hiệu.

D. giá trị lớn nhất.

Câu 4. Tam giác MNP có đường trung tuyến ME và trọng tâm G. Khi đó tỉ số \[\frac{{MG}}{{ME}}\] bằng :

A. \[\frac{2}{3}\]

B. \[\frac{3}{4}\]

C. \[\frac{1}{3}\]

D. \[\frac{3}{2}\]

II. Tự luận (7,0 điểm)

Bài 1. (1,5 điểm) Điều tra về số lượng học sinh nữ của mỗi lớp trong trường A được ghi lại ở bảng sau :

Giá trị (x)	16	17	18	19	20	22
Tần số (n)	4	2	5	2	3	4

a) Dấu hiệu ở đây là gì ? Trường A có bao nhiêu lớp?

b) Trung bình mỗi lớp của trường A có bao nhiêu học sinh nữ?

Bài 2. (2,5 điểm) Cho các đa thức:

A(x) = -5x - 6 + 6x³ - 12;

B(x) = x³ - 5x + 5x³ - 16 - 2x².

a) Thu gọn các đa thức A(x); B(x) và sắp xếp các hạng tử của chúng theo lũy thừa giảm dần của biến.

b) Tính A(x) + B(x).

c) Tính C(x) = A(x) - B(x) và tìm nghiệm của C(x).

Bài 3. (3,5 điểm) Cho tam giác ABC cân tại A, trung tuyến AM. Qua điểm B vẽ đường thẳng song song với đường thẳng AC, cắt đường thẳng AM tại điểm D.

a) Chứng minh \[\Delta AMC = \Delta DMB.\]

b) Chứng minh AB = BD.

c) Gọi P là trung điểm của đoạn thẳng AB, đoạn thẳng PD cắt đoạn thẳng BC tại điểm O. Trên tia đối của tia PO lấy điểm N sao cho PN = PO. Chứng minh điểm O là trọng tâm của \[\Delta AB{\rm{D}}\] và NA = 2OM.

Bài 4. (0,5 điểm) Tìm x để biểu thức P đạt giá trị nhỏ nhất:

P = \[\left| {x - 1} \right| + \left| {x - 4} \right| + \left| {x - 6} \right|\].

Đáp án và hướng dẫn giải

I. Trắc nghiệm (2,0 điểm) Khoanh tròn vào chữ cái đứng trước câu trả lời đúng

Câu 1. Bậc của đơn thức 2²x³y là:

A. 6. 

B. 5.

C. 3.

D. 4.

Hướng dẫn giải

Đáp án đúng là: D

Bậc của đơn thức 2²x³y là 3 + 1 = 4.

Chọn đáp án D.

Câu 2. Cho \[\Delta ABC\] biết BC = 4 cm, AB = 5 cm, AC = 3 cm. Khi đó ta có tam giác ABC:

A. nhọn.

B. vuông tại A.

C. vuông tại B.

D. vuông tại C.

Hướng dẫn giải

Đáp án đúng là: D

Ta có 5² = 25, 3² + 4² = 9 + 16 = 25.

Do đó AB² = AC² + BC² hay tam giác ABC vuông tại C.

Chọn đáp án D.

Câu 3. Giá trị có tần số lớn nhất được gọi là:

A. tần số của giá trị đó.

B. mốt của dấu hiệu.

C. số trung bình cộng của dấu hiệu.

D. giá trị lớn nhất.

Hướng dẫn giải

Đáp án đúng là: B

Giá trị có tần số lớn nhất được gọi là mốt của dấu hiệu (theo định nghĩa).

Chọn đáp án B.

Câu 4. Tam giác MNP có đường trung tuyến ME và trọng tâm G. Khi đó tỉ số \[\frac{{MG}}{{ME}}\] bằng:

A. \[\frac{2}{3}\]

B. \[\frac{3}{4}\]

C. \[\frac{1}{3}\]

D. \[\frac{3}{2}\]

Hướng dẫn giải

Đáp án đúng là: A

Ba đường trung tuyến của tam giác cùng đi qua một điểm. Điểm đó cách đỉnh một khoàng bằng \[\frac{2}{3}\] độ dài đường trung tuyến đi qua đỉnh đó nên \[\frac{{MG}}{{ME}} = \frac{2}{3}\].

Chọn đáp án A.

II. Tự luận (8,0 điểm)

Bài 1. (1,5 điểm)

a) Dấu hiệu là số lượng học sinh nữ của mỗi lớp trong trường A.

Trường A có 4 + 2 + 5 + 2 + 3 + 4 = 20 lớp.

b) Trung bình mỗi lớp của trường A có:

\[\frac{{16.4 + 17.2 + 18.5 + 19.2 + 20.3 + 22.4}}{{20}}\] = 18,7 ≈ 19 học sinh nữ.

Bài 2. (2,5 điểm) Cho các đa thức:

A(x) = -5x - 6 + 6x³ - 12;

B(x) = x³ - 5x + 5x³ - 16 - 2x².

a) Thu gọn các đa thức A(x); B(x) và sắp xếp các hạng tử của chúng theo lũy thừa giảm dần của biến.

b) Tính A(x) + B(x).

c) Tính C(x) = A(x) - B(x) và tìm nghiệm của C(x).

a) A(x) = -5x - 6 + 6x³ - 12

A(x) = 6x³ - 5x + (-6 - 12)

A(x) = 6x³ - 5x - 18

B(x) = x³ - 5x + 5x³ - 16 - 2x²

B(x) = (x³ + 5x³) - 2x² - 5x - 16

B(x) = 6x³ - 2x² - 5x - 16

b) A(x) + B(x) = 6x³ - 5x - 18 + 6x³ - 2x² - 5x - 16

A(x) + B(x) = (6x³ + 6x³) - 2x² + (-5x - 5x) + (-18 - 16)

A(x) + B(x) = 12x³ - 2x² - 10x - 10

c) C(x) = A(x) - B(x)

C(x) = 6x³ - 5x - 18 - (6x³ - 2x² - 5x - 16)

C(x) = 6x³ - 5x - 18 - 6x³ + 2x² + 5x + 16

C(x) = (6x³ - 6x³) + 2x² + (-5x + 5x) + (-18 + 16)

C(x) = 2x² - 2

Để C(x) = 0 thì 2x² - 2 = 0

\[ \Rightarrow \] 2x² = 2

\[ \Rightarrow \] x² = 1

Trường hợp 1. x² = 1²

\[ \Rightarrow \] x = 1

Trường hợp 2. x² = (-1)²

\[ \Rightarrow \] x = -1

Vậy x = 1 hoặc x = -1.

Bài 3. (3,5 điểm)

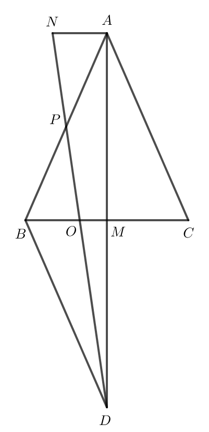
a) \[\Delta ABC\] cân tại A có M là trung điểm của BC nên AM vừa là đường trung tuyến, vừa là đường cao của \[\Delta ABC\].

Do đó \[A{\rm{D}} \bot BC\].

Do BD // AC nên \[\widehat {MB{\rm{D}}} = \widehat {MCA}\] (2 góc so le trong).

Xét \[\Delta AMC\] vuông tại M và \[\Delta DMB\] vuông tại M có:

\[\widehat {MCA} = \widehat {MBD}\] (chứng minh trên).

MB = MC (theo giả thiết).

\[ \Rightarrow \Delta AMC = \Delta DMB\] (góc nhọn - cạnh góc vuông)

b) Do \[\Delta AMC = \Delta DMB\] (góc nhọn - cạnh góc vuông) nên MA = MD (2 cạnh tương ướng).

Do đó M là trung điểm của AD.

\[\Delta AB{\rm{D}}\] có M là trung điểm của AD, lại có \[BM \bot A{\rm{D}}\] nên \[\Delta AB{\rm{D}}\] cân tại B.

c) Xét \[\Delta AB{\rm{D}}\] có BM, DP là các đường trung tuyến cắt nhau tại O nên O là trọng tâm của \[\Delta AB{\rm{D}}\].

Xét \[\Delta APN\] và \[\Delta BPO\] có:

AP = BP (theo giả thiết).

\[\widehat {APN} = \widehat {BPO}\] (2 góc đối đỉnh).

PN = PO (theo giả thiết).

\[ \Rightarrow \Delta APN = \Delta BPO\] (c - g - c).

\[ \Rightarrow \] NA = BO (2 cạnh tương ứng).

Do O là trọng tâm của \[\Delta AB{\rm{D}}\] nên BO = \[\frac{2}{3}\]BM; OM = \[\frac{1}{3}\]BM.

Do đó BO = 2OM.

Mà NA = BO nên NA = 2OM.

Vậy O là trọng tâm của \[\Delta AB{\rm{D}}\] và NA = 2OM.

Bài 5. (0,5 điểm)

P = \[\left| {x - 1} \right| + \left| {x - 4} \right| + \left| {x - 6} \right|\]

P = \[\left| {x - 6} \right| + \left| {x - 1} \right| + \left| {x - 4} \right|\]

P = \[\left| {6 - x} \right| + \left| {x - 1} \right| + \left| {x - 4} \right|\]

Ta có: \[\left| {6 - x} \right| + \left| {x - 1} \right| \ge \left| {6 - x + x - 1} \right| = 5\]; \[\left| {x - 4} \right| \ge 0.\]

Do đó \[\left| {6 - x} \right| + \left| {x - 1} \right| + \left| {x - 4} \right| \ge 5 + 0 = 5.\]

Dấu “=” xảy ra khi (6 - x)(x - 1) ≥ 0 và x - 4 = 0.

Suy ra x = 4.

Vậy giá trị nhỏ nhất của P = 5 khi x = 4. 

Bộ 21 Đề thi Toán lớp 7 Học kì 2 năm 2024 có đáp án – Đề 8

Phòng Giáo dục và Đào tạo .....

Đề thi Học kì 2 - Năm học 2024 - 2025

Bài thi môn: Toán lớp 7

Thời gian làm bài: 90 phút

(Đề 8)

Câu 1: (1.0 điểm) Điểm kiểm tra một tiết môn Toán của học sinh một lớp 7 tại một trường THCS được cho trong bảng tần số sau:

 

a) Dấu hiệu điều tra ở đây là gì ? Dấu hiệu có bao nhiêu giá trị khác nhau ?

b) Tìm Mốt. Tính số trung bình cộng.

 

Câu 2 : (2.0 điểm)

a) Thu gọn đơn thức A. Xác định phần hệ số và tìm bậc của đơn thức thu gọn, biết :

\[A = \left( { - \frac{3}{4}{x^2}{y^5}{z^3}} \right)\left( {\frac{5}{3}{x^3}{y^4}{z^2}} \right)\].

b) Tính giá trị của biểu thức \[C = 3{x^2}y - xy + 6\] tại x = 2, y = 1.

Câu 3 : (2.0 điểm) Cho hai đa thức :   \[M\left( x \right) = 3{x^4} - 2{x^3} + {x^2} + 4x - 5\]          

        \[N\left( x \right) = 2{x^3} + {x^2} - 4x - 5\]            

a) Tính \[M(x) + N(x)\] ;

b) Tìm đa thức P(x) biết : P(x) + N(x) = M(x).

Câu 4 : (1.0 điểm) Tìm nghiệm của các đa thức sau :

a) \[g(x) = x - \frac{1}{7}\] ;          

b) \[h(x) = 2x + 5\].

Câu 5 : (1.0 điểm) Tìm m để đa thức\[f(x) = \left( {m - 1} \right){x^2} - 3mx + 2\]có một nghiệm x = 1.

Câu 6 : (1.0 điểm) Cho \[\Delta ABC\]vuông tại A, biết AB = 6 cm, BC = 10cm. Tính độ dài cạnh AC và chu vi tam giác ABC.

Câu 7 : (2.0 điểm) Cho \[\Delta ABC\]vuông tại A, đường phân giác của góc B cắt AC tại D. Vẽ \[DH \bot BC\,\left( {H \in BC} \right)\].

a) Chứng minh : \[\Delta ABD = \Delta HBD\] ;

b) Trên tia đối của AB lấy điểm K sao cho AK = HC. Chứng minh ba điểm K, D, H thẳng hàng.

----------HẾT----------

 

Đáp án và hướng dẫn giải

Câu 1:

a) Dấu hiệu điều tra: “Điểm kiểm tra 1 tiết môn Toán của mỗi học sinh một lớp 7”    (0,25 điểm)

Số các giá trị khác nhau là 8. (0,25 điểm)

b) Mốt của dấu hiệu là 7 (vì đây giá trị có tần số lớn nhất: 11)           (0,25 điểm)

Số trung bình cộng:

\(\overline X  = \frac{{3.1 + 4.2 + 5.7 + 6.8 + 7.11 + 8.5 + 9.2 + 10.4}}{{40}} = \frac{{269}}{{40}} = 6,725\)              (0,25 điểm)

Câu 2:

a) \[A = \left( { - \frac{3}{4}{x^2}{y^5}{z^3}} \right)\left( {\frac{5}{3}{x^3}{y^4}{z^2}} \right) = \left( { - \frac{3}{4}.\frac{5}{3}} \right).\left( {{x^2}.{x^3}} \right).\left( {{y^5}.{y^4}} \right).\left( {{z^3}.{z^2}} \right) =  - \frac{5}{4}{x^5}{y^9}{z^5}\] 

(0,5 điểm)

Hệ số: \[ - \frac{5}{4}\]          (0,25 điểm)

Bậc của đơn thức A là 5 + 9 + 5 = 19.         (0,25 điểm)        

b) Thay x = 2; y = 1 vào biểu thức \[C = 3{x^2}y - xy + 6\] ta được:

\[C = {3.2^2}.1 - 2.1 + 6 = 16\]

Vậy C = 16 tại x = 2 và y = 1.    (1 điểm)

Câu 3:

a) \[M\left( x \right) = 3{x^4} - 2{x^3} + {x^2} + 4x - 5\];\[N\left( x \right) = 2{x^3} + {x^2} - 4x - 5\]

\[M\left( x \right) + N(x) = 3{x^4} + \left( { - 2{x^3} + 2{x^3}} \right) + \left( {{x^2} + {x^2}} \right) + \left( {4x - 4x} \right) + \left( { - 5 - 5} \right)\]

                   \[ = 3{x^4} + 2{x^2} - 10\]          (1 điểm)

b) Ta có: P(x) + N(x) = M(x) 

Nên \[P\left( x \right) = M\left( x \right) - N\left( x \right)\]

\[ = \left( {3{x^4} - 2{x^3} + {x^2} + 4x - 5} \right) - \left( {2{x^3} + {x^2} - 4x - 5} \right)\]

\[ = 3{x^4} + \left( { - 2{x^3} - 2{x^3}} \right) + \left( {{x^2} - {x^2}} \right) + \left( {4x + 4x} \right) + \left( { - 5 + 5} \right)\]

\[ = 3{x^4} - 4{x^3} + 8x\]                      (1 điểm)

Câu 4:

a) \[g(x) = 0 \Rightarrow x - \frac{1}{7} = 0 \Rightarrow x = \frac{1}{7}\]

Vậy \[x = \frac{1}{7}\] là nghiệm của đa thức \[g\left( x \right)\]                 (0,5 điểm)

b) \[h(x) = 0 \Rightarrow 2x + 5 = 0 \Rightarrow x =  - \frac{5}{2}\]

Vậy \[x =  - \frac{5}{2}\] là nghiệm của đa thức \[h\left( x \right)\]                 (0,5 điểm)

 

Câu 5:

\[f(x) = \left( {m - 1} \right){x^2} - 3mx + 2\]

\[x = 1\] là một nghiệm của đa thức f(x) nên ta có:

\[f(1) = \left( {m - 1} \right){.1^2} - 3m.1 + 2 = 0\]

\[ \Rightarrow  - 2m + 1 = 0 \Rightarrow m = \frac{1}{2}\]

Vậy với \[m = \frac{1}{2}\] đa thức f(x) có một nghiệm\[x = 1\].                           (1 điểm)

Câu 6:

Áp dụng định lý Py–ta–go vào tam giác vuông ABC ta có:

\[B{C^2} = A{B^2} + A{C^2}\]

\[\begin{array}{l} \Rightarrow A{C^2} = B{C^2} - A{B^2} = {10^2} - {6^2} = 64\\ \Rightarrow AC = \sqrt {64}  = 8cm\end{array}\]                      (0,5 điểm)

Chu vi \[\Delta ABC\]: AB + AC + BC = 6 + 8 + 10 = 24 cm       (0,5 điểm)

Câu 7:

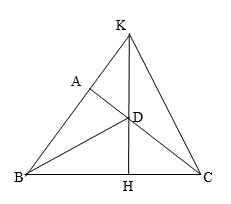
a) Xét hai tam giác vuông ABD và HBD có:

     BD là cạnh chung

     DA = DH (D nằm trên tia phân giác của góc B)

Do đó: \[\Delta ABD = \Delta HBD\] (cạnh huyền – cạnh góc vuông)      (1 điểm)  

b)

Từ câu a) có\[\Delta ABD = \Delta HBD \Rightarrow AB = BH\]

Mà AK = HC (gt)

Nên AB + AK = BH + HC

\( \Rightarrow \) BK = BC

Suy ra, \[\Delta BKC\]cân tại B.

Khi đó, BD vừa là phân giác, vừa là đường cao xuất phát từ đỉnh B

\[ \Rightarrow D\]là trực tâm của \[\Delta BKC\](Do D là giao của hai đường cao BD và AC)    (0,5 điểm)

Mặt khác, \[\Delta CAK = \Delta KHC\](c-g-c) \[ \Rightarrow KH \bot BC\]

\[ \Rightarrow \]KH là đường cao kẻ từ đỉnh K của \[\Delta BKC\] nên KH phải đi qua trực tâm D.

Vậy ba điểm K, D, H thẳng hàng.          (0,5 điểm)

 

-----------------------

Bộ 21 Đề thi Toán lớp 7 Học kì 2 năm 2024 có đáp án – Đề 9

Phòng Giáo dục và Đào tạo .....

Đề thi Học kì 2 - Năm học 2024 - 2025

Bài thi môn: Toán lớp 7

Thời gian làm bài: 90 phút

(Đề 9)

 

Bài 1. (2,0 điểm) Thời gian giải một bài toán của 30 học sinh được ghi lại trong bảng sau:

Giá trị (x)	5	7	9	10	12	15
Tần số (n)	3	4	7	9	5	2	N = 30

a) Dấu hiệu ở đây là gì ? Tính số trung bình cộng của dấu hiệu.

b) Tìm mốt của dấu hiệu.

Bài 2. (2,0 điểm) Cho đơn thức A = \[\left( {\frac{{ - 2}}{3}{x^3}{y^3}z} \right)\](-6xy³z).

a) Thu gọn, xác định hệ số và bậc của đơn thức A.

b) Tính giá trị của đơn thức A biết x = -1 ; y = 1 ; z = \[\frac{1}{2}\].

Bài 3. (2,0 điểm) Cho hai biểu thức

f(x) = -2x⁴ - 3x³ + 4x⁴ - x² + 5x + 3x² + 5x³ + 6; g(x) = x⁴ - x³ + x² - 5x - x³ - 2x² + 3.

a) Thu gọn và sắp xếp đa thức f(x) và g(x) theo lũy thừa giảm dần của biến; cho biết bậc; hệ số cao nhất; hệ số tự do của mỗi đa thức.

b) Tìm các đa thức h(x) và k(x), biết:

h(x) = f(x) + g(x); k(x) = f(x) - 2g(x) - 4x².

Bài 4. (3,5 điểm) Cho tam giác ABC vuông tại A, AC > AB. Đường trung trực của AB cắt BC tại I.

a) Chứng minh rằng \[\Delta AIB,\Delta AIC\] là các tam giác cân.

b) Từ I kẻ đường thẳng d vuông góc với BC, cắt tia BA và AC tại M và N; tia BN cắt CM tại E. Chứng minh rằng \[EB \bot MC.\]

c) Chứng minh rằng các đường thẳng EA và BC song song với nhau.

Bài 5. (0,5 điểm) Tính giá trị của biểu thức T = x³ - 2x² - xy² + 2xy + 10x + 10y

biết x + y = 2.

 

Đáp án và hướng dẫn giải

Bài 1. (1,5 điểm)

a) Dấu hiệu là thời gian giải một bài toán của 30 học sinh.

Trung bình cộng của dấu hiệu là:

\[\frac{{5.3 + 7.4 + 9.7 + 10.9 + 12.5 + 15.2}}{{30}} = \frac{{286}}{{30}}\] = 9,5(3) ≈ 9,5.

b) Mốt của dấu hiệu là 10.

Bài 2. (2,0 điểm)

a) A = \[\left( {\frac{{ - 2}}{3}{x^3}{y^3}z} \right)\](-6xy³z)

A = \[\left( {\frac{{ - 2}}{3}. - 6} \right)\].(x³.x).(y³.y³).(z.z)

A = \[\left( {\frac{{ - 2}}{3}. - 6} \right)\].(x³.x).(y³.y³).(z.z)

A = 4x⁴y⁶z²

Hệ số của đơn thức A: 4.

Bậc của đơn thức A: 4 + 6 + 2 = 12.

b) Với x = -1; y = 1; z = \[\frac{1}{2}\] thì A = 4.(-1)⁴.1⁶. \[{\left( {\frac{1}{2}} \right)^2}\] = 4.1.1.\[\frac{1}{4}\] = 1.

Vậy A = 1 với x = -1; y = 1; z = \[\frac{1}{2}\].

Bài 3. (3,0 điểm)

a) f(x) = -2x⁴ - 3x³ + 4x⁴ - x² + 5x + 3x² + 5x³ + 6

f(x) = (-2x⁴ + 4x⁴) + (- 3x³ + 5x³) + (- x² + 3x²) + 5x + 6

f(x) = 2x⁴ + 2x³ + 2x² + 5x + 6

Bậc của đa thức f(x): 4.

Hệ số cao nhất của đa thức f(x): 2.

Hệ số tự do của đa thức f(x): 6.

g(x) = x⁴ - x³ + x² - 5x - x³ - 2x² + 3

g(x) = x⁴ + (- x³ - x³) + (x² - 2x²) - 5x + 3

g(x) = x⁴ - 2x³ - x² - 5x + 3

Bậc của đa thức g(x): 4.

Hệ số cao nhất của đa thức g(x): 1.

Hệ số tự do của đa thức g(x): 3.

b) h(x) = f(x) + g(x)

h(x) = 2x⁴ + 2x³ + 2x² + 5x + 6 + x⁴ - 2x³ - x² - 5x + 3

h(x) = (2x⁴ + x⁴) + (2x³ - 2x³) + (2x² - x²) + (5x - 5x) + (6 + 3)

h(x) = 3x⁴ + x² + 9

k(x) = f(x) - 2g(x) - 4x²

k(x) = 2x⁴ + 2x³ + 2x² + 5x + 6 - 2(x⁴ - 2x³ - x² - 5x + 3) - 4x²

k(x) = 2x⁴ + 2x³ + 2x² + 5x + 6 - 2x⁴ + 4x³ + 2x² + 10x - 6 - 4x²

k(x) = (2x⁴ - 2x⁴) + (2x³ + 4x³) + (2x² + 2x² - 4x²) + (5x + 10x) + (6 - 6)

k(x) = 6x³ + 15x

Bài 4. (3,5 điểm)

 

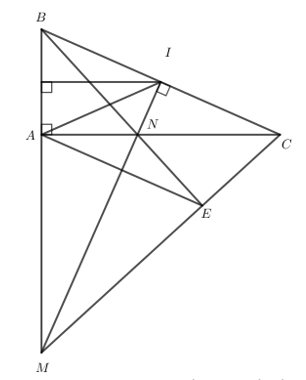
a) Do I nằm trên đường trung trực của AB nên AI = BI.

\[\Delta AIB\] có AI = BI nên \[\Delta AIB\] cân tại I.

Do đó \[\widehat {IAB} = \widehat {IBA}\].

Lại có: \[\widehat {IAB} + \widehat {IAC} = 90^\circ ;\] \[\widehat {IBA} + \widehat {IC{\rm{A}}} = 90^\circ \] nên \[\widehat {IAC} = \widehat {IC{\rm{A}}}\].

\[\Delta AIC\] có \[\widehat {IAC} = \widehat {IC{\rm{A}}}\] nên \[\Delta AIC\] cân tại I.

b) Xét \[\Delta MBC\] có \[CA \bot MB;\] \[MI \bot BC\].

Mà CA cắt MI tại N nên N là trực tâm của \[\Delta MBC\].

Do đó \[BN \bot MC\] hay \[BE \bot MC\].

c) \[\Delta MBC\]có MI vừa là đường trung tuyến, vừa là đường cao nên \[\Delta MBC\] cân tại M.

Khi đó MI là đường phân giác của \[\widehat {BMC}.\]

\[ \Rightarrow \widehat {AMN} = \widehat {EMN}\].

Xét \[\Delta AMN\] vuông tại A và \[\Delta EMN\] vuông tại E có:

MN chung.

\[\widehat {AMN} = \widehat {EMN}\] (chứng minh trên).

\[ \Rightarrow \Delta AMN = \Delta EMN\] (cạnh huyền - góc nhọn).

\[ \Rightarrow \] MA = ME (2 cạnh tương ứng).

\[\Delta MA{\rm{E}}\] có MA = ME nên \[\Delta MA{\rm{E}}\] cân tại M.

Do đó \[\widehat {MA{\rm{E}}} = \widehat {ME{\rm{A}}}\].

Xét \[\Delta MA{\rm{E}}\] có \[\widehat {MA{\rm{E}}} + \widehat {ME{\rm{A}}} + \widehat {AM{\rm{E}}} = 180^\circ \]

\[ \Rightarrow 2\widehat {MA{\rm{E}}} + \widehat {AM{\rm{E}}} = 180^\circ \]

\[ \Rightarrow \widehat {MA{\rm{E}}} = \frac{{180^\circ  - \widehat {AM{\rm{E}}}}}{2}\] (1).

Do \[\Delta MBC\] cân tại M nên \[\widehat {MBC} = \widehat {MCB}\].

Xét \[\Delta MBC\] có \[\widehat {MBC} + \widehat {MCB} + \widehat {BMC} = 180^\circ \]

\[ \Rightarrow 2\widehat {MBC} + \widehat {BMC} = 180^\circ \]

\[ \Rightarrow \widehat {MBC} = \frac{{180^\circ  - \widehat {BMC}}}{2}\] (2).

Từ (1) và (2) suy ra \[\widehat {MA{\rm{E}}} = \widehat {MBC}\].

Mà hai góc này ở vị trí đồng vị nên EA // BC.

Vậy hai đường thẳng EA và BC song song với nhau.

Bài 5. (0,5 điểm)

T = x³ - 2x² - xy² + 2xy + 10x + 10y

T = x²(x - 2) - xy(y - 2) + 10(x + y)

T = x².(-y) - xy.(-x) + 10.2

T = -x²y + x²y + 20

T = 20.

Vậy T = 20

  

Bộ 21 Đề thi Toán lớp 7 Học kì 2 năm 2024 có đáp án - Đề 10

Phòng Giáo dục và Đào tạo .....

Đề thi Học kì 2 - Năm học 2024 - 2025

Bài thi môn: Toán lớp 7

Thời gian làm bài: 90 phút

(Đề 10)

Câu 1: (2.0 điểm) Điểm kiểm tra 1 tiết đại số của học sinh lớp 7A được ghi lại như sau:

             6        4        9        7        8        8        4        8        8        10

               

10      9        8        7        7        6        6        8        5        6

               

4        9        7        6        6        7        4        10      9        8

a) Lập bảng tần số;

b) Tính số trung bình cộng và tìm mốt của dấu hiệu.  

Câu 2: (1.5 điểm) Cho đơn thức \[P = \left( {\frac{2}{3}{x^2}y} \right)\left( {\frac{9}{2}xy} \right)\]

a) Thu gọn và xác định hệ số, phần biến, bậc của đơn thức P;

b) Tính giá trị của P tại x = –1 và y = 2.

                

Câu 3: (1.5 điểm) Cho 2 đa thức sau:

        A(x) =  4x³ – 7x² + 3x – 12 

         B(x) = – 2x³ + 2x² + 12 + 5x² – 9x 

a) Thu gọn và sắp xếp đa thức B(x) theo lũy thừa giảm dần của biến;

b) Tính  A(x) + B(x) và  B(x) – A(x)­­.       

     

Câu 4: (1.5 điểm) Tìm nghiệm của các đa thức sau:

          a) M(x) = 2x – 6;  

          b) N(x) = x² + 2x + 2015.

Câu 5: (3.5 điểm) Cho ∆ABC vuông tại A, vẽ trung tuyến AM (M Î BC). Từ M kẻ MH\( \bot \)AC (H \( \in \)AC), trên tia đối của tia MH lấy điểm K sao cho MK = MH.

a) Chứng minh ∆MHC = ∆MKB;

b) Chứng minh AB // MH;

c) Gọi G là giao điểm của BH và AM, I là trung điểm của AB. Chứng minh I, G, C thẳng hàng.

--------------HẾT--------------

Đáp án và hướng dẫn giải

Câu 1: a) Lập bảng tần số:                 (1 điểm)                                           

Giá trị (x)	4	5	6	7	8	9	10
Tần số (n)	4	1	6	5	7	4	3	N  = 30

b) Số trung bình cộng của dấu hiệu là:

 \[\overline X  = \frac{{4.4 + 5.1 + 6.6 + 7.5 + 8.7 + 9.4 + 10.3}}{{30}} = \]\[\frac{{214}}{{30}}\]\[ \approx \]7,13 (0,5 điểm)

Mốt của dấu hiệu là: \({M_0} = 8\).  (0,5 điểm)

Câu 2:

a) \[P = \left( {\frac{2}{3}{x^2}y} \right)\left( {\frac{9}{2}xy} \right)\]\( = \left( {\frac{2}{3}.\frac{9}{2}} \right).\left( {{x^2}.x} \right).\left( {y.y} \right) = \) 3x³y²

Hệ số: 3

Phần biến: x³y²

Bậc của đơn thức: 5                              (1 điểm, mỗi ý nhỏ 0,25 điểm)

b) Thay x = –1 và y = 2 vào đơn thức P

P = 3.( –1)³.2² = –12

Vậy P = –12 tại x = –1 và y = 2.   (0,5 điểm)

Câu 3:

a)  B(x) = –2x³ + 2x² + 12 + 5x² – 9x 

 = –2x³ + (2x² + 5x²) + 12 – 9x 

 = –2x³ + 7x² + 12 – 9x 

Sắp xếp: B(x) = –2x³ + 7x² – 9x + 12              (0,5 điểm)

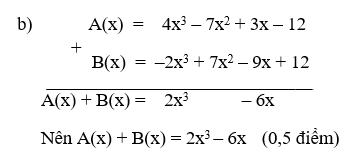
Câu 4:

a) M(x) = 2x – 6   

           Ta có: M(x) = 0 hay 2x – 6 =0

                                             2x = 6

                                               x = 3

Vậy nghiệm của đa thức M(x) là x = 3.  (1 điểm)

b) N(x) = x² + 2x + 2015

Ta có:  x² + 2x + 2015 = x² + x + x + 1 + 2014

                                     = x(x + 1) + (x + 1) + 2014

                                     = (x + 1)(x + 1) + 2014

                                     = (x + 1)² + 2014

Vì (x + 1)² \( \ge \) 0 với mọi x

\( \Rightarrow \) (x + 1)² + 2014 \( \ge \) 2014 > 0 với mọi x

\( \Rightarrow \) N(x) > 0 với mọi x

Vậy đa thức N(x) không có nghiệm.     (0,5 điểm)

Câu 5: Vẽ hình đúng, ghi GT, KL (0,5 điểm)

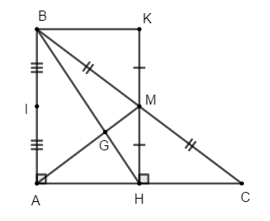
a) Xét  ∆MHC và ∆MKB có

    MH = MK (gt)

    \[\widehat {{\rm{HMC}}}{\rm{ }} = {\rm{ }}\widehat {{\rm{KMB}}}{\rm{ }}\](hai góc đối đỉnh)

               MC = MB (M là trung điểm của BC)

     Do đó:  ∆MHC = ∆MKB (c.g.c)   (1 điểm)

b) Ta có  MH\( \bot \)AC (gt)

                AB\( \bot \)AC (∆ABC vuông tại A)

       Nên AB // MH.                                                  (1 điểm)

c) Xét ∆ABH vuông tại A và ∆KHB vuông tại H có:

BH: cạnh huyền chung

\(\widehat {ABH} = \widehat {KHB}\)  (AB // MH)

Do đó: ∆ABH = ∆KHB (ch-gn)

\( \Rightarrow \) AH = BK (hai cạnh tương ứng)

Mà BK = HC (∆MHC = ∆MKB)

Nên AH = HC \( \Rightarrow \) H là trung điểm của AC

Do đó G là giao điểm của hai trung tuyến BH và AM trong tam giác ABC

\( \Rightarrow \)G là trọng tâm của tam giác ABC

Mà CI là trung tuyến của tam giác ABC (do I là trung điểm của AB)

Vậy G thuộc trung tuyến CI hay I, G, C thẳng hàng.  (1 điểm)

-----------------------

Bộ 21 Đề thi Toán lớp 7 Học kì 2 năm 2024 có đáp án - Đề 11

Phòng Giáo dục và Đào tạo .....

Đề thi Học kì 2 - Năm học 2024 - 2025

Bài thi môn: Toán lớp 7

Thời gian làm bài: 90 phút

(Đề 11)

I. Trắc nghiệm (2,0 điểm) Khoanh tròn vào chữ cái đứng trước câu trả lời đúng

Câu 1. Cho đơn thức T = 3x²y³z. Đơn thức nào sau đây sau khi thu gọn đồng dạng với T.

A. x²y²zx.

B. xy²zxy.

C. x²zy²z².

D. x²yxz.

Câu 2. Cho đa thức P(x) = x³ - 6x² + 11x - 6. Giá trị nào sau đây KHÔNG là nghiệm của P(x) ?

A. 1.

B. 2.

C. 3.

D. 4.

Câu 3. Tam giác ABC có \[\widehat A = 43^\circ \] và \[\widehat B = 69^\circ \]. Thứ tự nào sau đây đúng ?

A. BC < CA < AB.

B. AB < CA < BC.

C. BC < AB < CA.

D. AB < BC < CA.

Câu 4. Cho tam giác ABC cân ở A. Đường phân giác AD và trung tuyến CE cắt nhau tại H. Đường thẳng BH

A. chứa phân giác trong đỉnh B.

B. chứa đường cao kẻ từ B.

C. chứa trung tuyến kẻ từ B.

D. cả ba đáp án A, B và C đều đúng.

II. Tự luận (8,0 điểm)

Bài 1. (2,0 điểm) Cho hai đa thức:

P(x) = x⁴ + 3x³ - x + \[\frac{1}{2}\] - x³ - 4x ;      Q(x) = \[\frac{3}{2}\] - 4x³ + x⁴ - 2x - 3x + 2x³.

a) Thu gọn và sắp xếp các đa thức P(x), Q(x) theo lũy thừa giảm dần của biến ;

b) Tính P(x) + Q(x); P(x) - Q(x).

Bài 2. (2,0 điểm) Cho các đa thức

A(x) = 12x³ + 2ax + a²

B(x) = 2x² - \[\left| {2{\rm{a}} + 3} \right|\]x + a²

Tìm a biết A(1) = B(-2).

Bài 3. (3,5 điểm) Cho tam giác ABC cân tại A có đường cao AD.

a) Tính BC biết AB = 13 cm và AD = 12 cm.

b) Kẻ DI vuông góc với AB tại I. Lấy điểm M trên cạnh AB sao cho I là trung điểm của đoạn thẳng BM. Chứng minh DM = \[\frac{1}{2}\]BC.

c) Gọi H là giao điểm của AD và CM, N là giao điểm của BH và AC. Lấy E là điểm thuộc tia đối của tia ID sao cho ID = IE. Chứng minh 3 điểm E, M, N thẳng hàng.

Bài 4. (0,5 điểm) Tìm tất cả các số nguyên dương x, y thỏa mãn:

\[\frac{9}{{xy}} - \frac{1}{y} = 2 + \frac{3}{x}\].

 

Đáp án và hướng dẫn giải

I. Trắc nghiệm (2,0 điểm) Khoanh tròn vào chữ cái đứng trước câu trả lời đúng

Câu 1. Cho đơn thức T = 3x²y³z. Đơn thức nào sau đây sau khi thu gọn đồng dạng với T.

A. x²y²zx.

B. xy²zxy.

C. x²zy²z².

D. x²yxz.

Hướng dẫn giải

Đáp án đúng là: B

Ta có x²y²zx = (x².x).y².z = x³y²z ≠ x²y³z.

xy²zxy = (x.x).(y².y).z = x²y³z.

x²zy²z² = x²y².(z.z²) = x²y²z³ ≠ x²y³z.

x²yxz = (x².x)yz = x³yz ≠ x²y³z.

Do đó chọn đáp án B.

Câu 2. Cho đa thức P(x) = x³ - 6x² + 11x - 6. Giá trị nào sau đây KHÔNG là nghiệm của P(x)?

A. 1.

B. 2.

C. 3.

D. 4.

Hướng dẫn giải

Đáp án đúng là: D

Với x = 1 thì P(1) = 1³ - 6.1² + 11.1 - 6 = 1 - 6 + 11 - 6 = 0.

Do đó x = 1 là nghiệm của P(x).

Với x = 2 thì P(2) = 2³ - 6.2² + 11.2 - 6 = 8 - 6.4 + 22 - 6 = 8 - 24 + 22 - 6 = 0.

Do đó x = 2 là nghiệm của P(x).

Với x = 3 thì P(3) = 3³ - 6.3² + 11.3 - 6 = 27 - 6.9 + 33 - 6 = 27 - 54 + 33 - 6 = 0.

Do đó x = 3 là nghiệm của P(x).

Với x = 4 thì P(4) = 4³ - 6.4² + 11.4 - 6 = 64 - 96 + 44 - 6 = 6 ≠ 0.

Do đó x = 4 là nghiệm của P(x).

Câu 3. Tam giác ABC có \[\widehat A = 43^\circ \] và \[\widehat B = 69^\circ \]. Thứ tự nào sau đây đúng?

A. BC < CA < AB.

B. AB < CA < BC.

C. BC < AB < CA.

D. AB < BC < CA.

Hướng dẫn giải

Đáp án đúng là: C

Xét \[\Delta ABC\]: \[\widehat A + \widehat B + \widehat C = 180^\circ \].

Khi đó \[\widehat C = 180^\circ  - \widehat A - \widehat B\] = 180^o - 43^o - 69^o = 68^o.

Do 43^o < 68^o < 69^o nên \[\widehat A < \widehat C < \widehat B\].

Trong một tam giác, cạnh đối diện với góc lớn hơn thì lớn hơn nên \[\widehat A < \widehat C < \widehat B\] thì

BC < AB < CA.

Câu 4. Cho tam giác ABC cân ở A. Đường phân giác AD và trung tuyến CE cắt nhau tại H. Đường thẳng BH

A. chứa phân giác trong đỉnh B.

B. chứa đường cao kẻ từ B.

C. chứa trung tuyến kẻ từ B.

D. cả ba đáp án A, B và C đều đúng.

Hướng dẫn giải

Đáp án đúng là: C

\[\Delta ABC\] cân ở A có AD là đường phân giác nên AD vừa là đường phân giác, vừa là đường trung tuyến của \[\Delta ABC\].

\[\Delta ABC\] có hai đường trung tuyến AD và CE cắt nhau tại H nên H là trọng tâm \[\Delta ABC\].

Do đó BH chứa trung tuyến kẻ từ đỉnh B.

II. Tự luận (7,0 điểm)

Bài 1. (2,0 điểm)

P(x) = x⁴ + 3x³ - x + \[\frac{1}{2}\] - x³ - 4x;     

Q(x) = \[\frac{3}{2}\] - 4x³ + x⁴ - 2x - 3x + 2x³.

a) P(x) = x⁴ + 3x³ - x + \[\frac{1}{2}\] - x³ - 4x

P(x) = x⁴ + (3x³ - x³) + (-x - 4x) + \[\frac{1}{2}\]

P(x) = x⁴ + 2x³ - 5x + \[\frac{1}{2}\]

Q(x) = \[\frac{3}{2}\] - 4x³ + x⁴ - 2x - 3x + 2x³

Q(x) = x⁴ + (-4x³ + 2x³) + (-2x - 3x) + \[\frac{3}{2}\]

Q(x) = x⁴ - 2x³ - 5x + \[\frac{3}{2}\]

b) P(x) + Q(x) = x⁴ + 2x³ - 5x + \[\frac{1}{2}\] + x⁴ - 2x³ - 5x + \[\frac{3}{2}\]

P(x) + Q(x) = (x⁴ + x⁴) + (2x³ - 2x³) + (-5x - 5x) + \[\left( {\frac{1}{2} + \frac{3}{2}} \right)\]

P(x) + Q(x) = 2x⁴ - 10x + 1

P(x) - Q(x) = x⁴ + 2x³ - 5x + \[\frac{1}{2}\] - (x⁴ - 2x³ - 5x + \[\frac{3}{2}\])

P(x) - Q(x) = x⁴ + 2x³ - 5x + \[\frac{1}{2}\] - x⁴ + 2x³ + 5x - \[\frac{3}{2}\]

P(x) - Q(x) = (x⁴ - x⁴) + (2x³ + 2x³) + (-5x + 5x) + \[\left( {\frac{1}{2} - \frac{3}{2}} \right)\]

P(x) - Q(x) = 4x³ - 1

Bài 2. (2,0 điểm)

A(x) = 12x³ + 2ax + a²

B(x) = 2x² - \[\left| {2{\rm{a}} + 3} \right|\]x + a²

Với x = 1 ta có A(1) = 12.1³ + 2.a.1 + a² = 12 + 2a + a².

Với x = -2 ta có B(-2) = 2.(-2)² -\[\left| {2{\rm{a}} + 3} \right|\].(-2) + a² = 9 + 2\[\left| {2{\rm{a}} + 3} \right|\] + a².

Do A(1) = B(-2) nên 12 + 2a + a² = 9 + 2\[\left| {2{\rm{a}} + 3} \right|\] + a².

\[ \Rightarrow \] 12 + 2a + a² - 9 - a² = 2\[\left| {2{\rm{a}} + 3} \right|\].

\[ \Rightarrow \] (12 - 9) + (a² - a²) + 2a = 2\[\left| {2{\rm{a}} + 3} \right|\].

\[ \Rightarrow \] 3 + 2a = 2\[\left| {2{\rm{a}} + 3} \right|\].

Xét 2a + 3 ≥ 0 hay a ≥ \[\frac{{ - 3}}{2}\], khi đó \[\left| {2{\rm{a}} + 3} \right|\] = 2a + 3.

Do đó 3 + 2a = 2(2a + 3).

\[ \Rightarrow \] 3 + 2a = 4a + 6

\[ \Rightarrow \]2a - 4a = 6 - 3

\[ \Rightarrow \] -2a = 3

\[ \Rightarrow \] a = \[\frac{{ - 3}}{2}\] (thỏa mãn)

Xét 2a + 3 < 0 hay a < \[\frac{{ - 3}}{2}\],  khi đó \[\left| {2{\rm{a}} + 3} \right|\] = -(2a + 3).

Do đó 3 + 2a = -2(2a + 3).

\[ \Rightarrow \] 3 + 2a = -4a - 6

\[ \Rightarrow \] 2a + 4a = -6 - 3

\[ \Rightarrow \] 6a = -9

\[ \Rightarrow \] a = \[\frac{{ - 9}}{6}\]

\[ \Rightarrow \] a = \[\frac{{ - 3}}{2}\] (loại)

Vậy a = \[\frac{{ - 3}}{2}\].

Bài 3. (3,5 điểm)

 

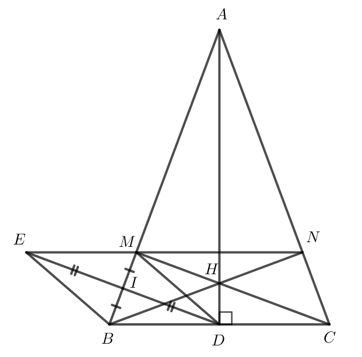
a) \[\Delta ABC\] cân tại A có AD là đường cao nên AD cũng là đường trung tuyến.

Do đó D là trung điểm của BC.

Áp dụng định lý Pytago vào \[\Delta AB{\rm{D}}\] vuông tại D ta có:

AD² + BD² = AB²

\[ \Rightarrow \] 12² + BD² = 13²

\[ \Rightarrow \] BD² = 169 - 144

\[ \Rightarrow \] BD² = 25

\[ \Rightarrow \] BD = 5 cm.

Do D là trung điểm của BC nên BD = \[\frac{1}{2}\]BC.

Do đó BC = 10 cm.

b) Xét \[\Delta DIM\] vuông tại I và \[\Delta DIB\] vuông tại I có:

ID chung.

IM = IB (theo giả thiết).

\[ \Rightarrow \Delta DIM = \Delta DIB\] (2 cạnh góc vuông).

\[ \Rightarrow \] DM = DB (2 cạnh tương ứng).

Mà DB = \[\frac{1}{2}\]BC nên DM = \[\frac{1}{2}\]BC.

c) \[\Delta MBC\] có MD = DB = DC = \[\frac{1}{2}\]BC nên \[\Delta MBC\] vuông tại M.

Do đó \[CM \bot AB.\]

\[\Delta ABC\] có \[A{\rm{D}} \bot BC;\] \[CM \bot AB\].

Mà AD cắt CM tại H nên H là trực tâm của \[\Delta ABC\].

Do đó \[BH \bot AC\] hay \[BN \bot AC\].

Do \[\Delta ABC\] cân tại A nên AB = AC và \[\widehat {ABC} = \widehat {ACB}\].

Xét \[\Delta ANB\] vuông tại N và \[\Delta AMC\] vuông tại M:

\[\widehat A\] chung.

AB = AC (chứng minh trên).

\[ \Rightarrow \Delta ANB = \Delta AMC\] (cạnh huyền - góc nhọn).

\[ \Rightarrow \] AN = AM (2 cạnh tương ứng).

\[\Delta AMN\] có AN = AM nên \[\Delta AMN\] cân tại A.

Do đó \[\widehat {AMN} = \widehat {ANM}\].

Xét \[\Delta AMN\] có \[\widehat {AMN} + \widehat {ANM} + \widehat {MAN} = 180^\circ \]

\[ \Rightarrow 2\widehat {AMN} + \widehat {MAN} = 180^\circ \]

\[ \Rightarrow \widehat {AMN} = \frac{{180^\circ  - \widehat {MAN}}}{2}\] (1).

Xét \[\Delta ABC\] có \[\widehat {ABC} + \widehat {ACB} + \widehat {BAC} = 180^\circ \]

\[ \Rightarrow 2\widehat {ABC} + \widehat {BAC} = 180^\circ \]

\[ \Rightarrow \widehat {ABC} = \frac{{180^\circ  - \widehat {BAC}}}{2}\] (2).

Từ (1) và (2) suy ra \[\widehat {AMN} = \widehat {ABC}\].

Mà hai góc này ở vị trí đồng vị nên MN // BC (3).

Xét \[\Delta EIM\] và \[\Delta DIB\] có:

EI = DI (theo giả thiết).

\[\widehat {EIM} = \widehat {DIB}\] (2 góc đối đỉnh).

IM = IB (theo giả thiết).

\[ \Rightarrow \Delta EIM = \Delta DIB\] (c - g - c).

\[ \Rightarrow \widehat {EMI} = \widehat {DBI}\] (2 góc tương ứng).

Mà hai góc này ở vị trí so le trong nên EM // BD hay EM // BC (4).

Từ (3) và (4) suy ra E, M, N thẳng hàng.

Vậy E, M, N thẳng hàng.

Bài 4. (0,5 điểm)

\[\frac{9}{{xy}} - \frac{1}{y} = 2 + \frac{3}{x}\]

\[ \Rightarrow \frac{9}{{xy}} - \frac{x}{{xy}} = \frac{{2{\rm{x}}y}}{{xy}} + \frac{{3y}}{{xy}}\]

Khử mẫu ta được: 9 - x = 2xy + 3y

\[ \Rightarrow \] 9 = x + 2xy + 3y

\[ \Rightarrow \] 9 = x(1 + 2y) + \[\frac{3}{2}\].2y

\[ \Rightarrow \] 9 + \[\frac{3}{2}\] = x(1 + 2y) + \[\frac{3}{2}\].2y + \[\frac{3}{2}\]

\[ \Rightarrow \]\[\frac{{18}}{2} + \frac{3}{2}\] = x(1 + 2y) + \[\frac{3}{2}\].(2y + 1)

\[ \Rightarrow \]\[\frac{{21}}{2}\] = (1 + 2y)(x + \[\frac{3}{2}\])

\[ \Rightarrow \]21 = (1 + 2y)(2x + 3)

Do x và y các số nguyên dương nên x ≥ 1; y ≥ 1.

Khi đó 2x + 3 ≥ 5; 2y + 1 ≥ 3.

Mà 21 = (1 + 2y)(2x + 3) nên 2x + 3 = 7; 2y + 1 = 3.

+) 2x + 3 = 7

\[ \Rightarrow \] 2x = 4

\[ \Rightarrow \] x = 2

+) 2y + 1 = 3

\[ \Rightarrow \] 2y = 2

\[ \Rightarrow \] y = 1

Vậy x = 2; y = 1.

 

Bộ 21 Đề thi Toán lớp 7 Học kì 2 năm 2024 có đáp án - Đề 12

Phòng Giáo dục và Đào tạo .....

Đề thi Học kì 2 - Năm học 2024 - 2025

Bài thi môn: Toán lớp 7

Thời gian làm bài: 90 phút

(Đề 12)

Câu 1: (2 điểm) Điều tra về điểm kiểm tra học kỳ II môn toán của học sinh lớp 7A, người điều tra có kết quả sau:

         

6	9	8	7	7	10	5
8	10	6	7	8	6	5
9	8	5	7	7	7	4
6	7	6	9	3	6	10
8	7	7	8	10	8	6

 

a) Lập bảng tần số, tính số trung bình cộng;

b) Tìm Mốt của dấu hiệu.

Câu 2: (1.5 điểm) Cho đơn thức \({\rm{A}} = {\left( { - {\rm{3}}{{\rm{a}}^{\rm{3}}}{\rm{x}}{{\rm{y}}^{\rm{3}}}} \right)^{\rm{2}}}{\left( { - \frac{{\rm{1}}}{{\rm{2}}}{\rm{a}}{{\rm{x}}^{\rm{2}}}} \right)^{\rm{3}}}\) (a là hằng số khác 0)

a) Thu gọn rồi cho biết phần hệ số và phần biến của A;

b) Tìm bậc của đơn thức A.

 

Câu 3: (2.5 điểm) Cho hai đa thức:

\({\rm{A}}\left( {\rm{x}} \right) = {\rm{4}}{{\rm{x}}^{\rm{4}}} + {\rm{6}}{{\rm{x}}^{\rm{2}}} - {\rm{7}}{{\rm{x}}^{\rm{3}}} - {\rm{5x}} - {\rm{6}}\) và \({\rm{B}}\left( {\rm{x}} \right) =  - {\rm{5}}{{\rm{x}}^{\rm{2}}} + {\rm{7}}{{\rm{x}}^{\rm{3}}} + {\rm{5x}} + {\rm{4}} - {\rm{4}}{{\rm{x}}^{\rm{4}}}\)

a) Tính M(x) = A(x) + B(x) rồi tìm nghiệm của đa thức M(x);

b) Tìm đa thức C(x) sao cho C(x) + B(x) = A(x)

 

Câu 4: (0.5 điểm) Cho 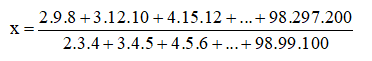. Hỏi x có phải là nghiệm của đa thức P(x) = x² - 12x + 35 không? Vì sao?

Câu 5: (3.5 điểm) Cho ΔABC vuông tại A, đường trung tuyến CM

a) Cho biết BC = 10cm, AC = 6cm. Tính độ dài đoạn thẳng AB, BM;

b) Trên tia đối của tia MC lấy điểm D sao cho MD = MC.

Chứng minh rằng ΔMAC = ΔMBD và AC = BD;

c) Chứng minh rằng AC + BC > 2CM;

d) Gọi K là điểm trên đoạn thẳng AM sao cho \({\rm{AK}} = \frac{{\rm{2}}}{{\rm{3}}}{\rm{AM}}\). Gọi N là giao điểm của CK và AD, I là giao điểm của BN và CD. Chứng minh rằng: CD = 3ID.

 

--------------HẾT--------------

 

Đáp án và hướng dẫn giải

Câu 1:

a) Lập bảng tần số, tính số trung bình cộng (1 điểm)

         

Giá trị (x)	Tần số (n)	Tích (x.n)	Số trung bình cộng
3	1	3	\(\begin{array}{l}\overline {\rm{X}}  = \frac{{{\rm{250}}}}{{{\rm{35}}}} = \frac{{{\rm{50}}}}{{\rm{7}}}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \approx 7,14\end{array}\)
4	1	4
5	3	15
6	7	42
7	9	63
8	7	56
9	3	27
10	4	40
	N = 35	Tổng: 250

 

b) Mốt của dấu hiệu là: \({{\rm{M}}_{\rm{0}}} = {\rm{7}}\). (1 điểm)

Câu 2:

          a) Ta có \({\rm{A}} = {\left( { - {\rm{3}}{{\rm{a}}^{\rm{3}}}{\rm{x}}{{\rm{y}}^{\rm{3}}}} \right)^{\rm{2}}}{\left( { - \frac{{\rm{1}}}{{\rm{2}}}{\rm{a}}{{\rm{x}}^{\rm{2}}}} \right)^{\rm{3}}}\)

           

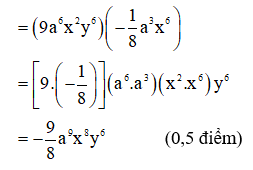
          Phần hệ số của A là: \(\frac{{ - {\rm{9}}}}{{\rm{8}}}{{\rm{a}}^{\rm{9}}}\) (vì a là hằng số)                (0,25 điểm)

          Phần biến của A là: \({{\rm{x}}^{\rm{8}}}{{\rm{y}}^{\rm{6}}}\)           (0,25 điểm)

b) Bậc của đơn thức A là: \(8 + 6 = 14\)                  (0,5 điểm)

Câu 3:        

          a) Ta có \({\rm{M}}\left( {\rm{x}} \right) = {\rm{A}}\left( {\rm{x}} \right) + {\rm{B}}\left( {\rm{x}} \right)\)

                            

                             \( = \left( {{\rm{4}}{{\rm{x}}^{\rm{4}}} + {\rm{6}}{{\rm{x}}^{\rm{2}}} - {\rm{7}}{{\rm{x}}^{\rm{3}}} - {\rm{5x}} - {\rm{6}}} \right) + \left( { - {\rm{5}}{{\rm{x}}^{\rm{2}}} + {\rm{7}}{{\rm{x}}^{\rm{3}}} + {\rm{5x}} + {\rm{4}} - {\rm{4}}{{\rm{x}}^{\rm{4}}}} \right)\)

                             \( = {{\rm{x}}^{\rm{2}}} - {\rm{2}}\)                 (1 điểm)

          Ta có \({{\rm{x}}^{\rm{2}}} - {\rm{2}} = {\rm{0}}\)

                     \(\begin{array}{l}{{\rm{x}}^{\rm{2}}} = 2\\{x^2} = {\left( {\sqrt 2 } \right)^2} = {\left( { - \sqrt 2 } \right)^2}\end{array}\)

                    Suy ra  \({\rm{x}} =  - \sqrt {\rm{2}} \) hoặc \({\rm{x}} = \sqrt {\rm{2}} \)

          Vậy nghiệm của đa thức M(x) là: \({\rm{x}} =  - \sqrt {\rm{2}} \) hoặc \({\rm{x}} = \sqrt {\rm{2}} \)     (0,5 điểm)

b) Ta có \({\rm{C}}\left( {\rm{x}} \right) + {\rm{B}}\left( {\rm{x}} \right) = {\rm{A}}\left( {\rm{x}} \right)\)

Suy ra   \({\rm{C}}\left( {\rm{x}} \right) = {\rm{A}}\left( {\rm{x}} \right) - {\rm{B}}\left( {\rm{x}} \right)\)\( = \left( {{\rm{4}}{{\rm{x}}^{\rm{4}}} + {\rm{6}}{{\rm{x}}^{\rm{2}}} - {\rm{7}}{{\rm{x}}^{\rm{3}}} - {\rm{5x}} - {\rm{6}}} \right) - \left( { - {\rm{5}}{{\rm{x}}^{\rm{2}}} + {\rm{7}}{{\rm{x}}^{\rm{3}}} + {\rm{5x}} + {\rm{4}} - {\rm{4}}{{\rm{x}}^{\rm{4}}}} \right)\)

\( = {\rm{4}}{{\rm{x}}^{\rm{4}}} + {\rm{6}}{{\rm{x}}^{\rm{2}}} - {\rm{7}}{{\rm{x}}^{\rm{3}}} - {\rm{5x}} - {\rm{6}} + {\rm{5}}{{\rm{x}}^{\rm{2}}} - {\rm{7}}{{\rm{x}}^{\rm{3}}} - {\rm{5x}} - {\rm{4}} + {\rm{4}}{{\rm{x}}^{\rm{4}}}\)

                                      \( = \left( {{\rm{4}}{{\rm{x}}^{\rm{4}}} + {\rm{4}}{{\rm{x}}^{\rm{4}}}} \right) + \left( { - {\rm{7}}{{\rm{x}}^{\rm{3}}} - {\rm{7}}{{\rm{x}}^{\rm{3}}}} \right) + \left( {{\rm{6}}{{\rm{x}}^{\rm{2}}} + {\rm{5}}{{\rm{x}}^{\rm{2}}}} \right) + \left( { - {\rm{5x}} - {\rm{5x}}} \right) + \left( { - {\rm{6}} - {\rm{4}}} \right)\)

\( = {\rm{8}}{{\rm{x}}^{\rm{4}}} - {\rm{14}}{{\rm{x}}^{\rm{3}}} + {\rm{11}}{{\rm{x}}^{\rm{2}}} - {\rm{10x}} - {\rm{10}}\)             

          Vậy \(C\left( x \right) = {\rm{8}}{{\rm{x}}^{\rm{4}}} - {\rm{14}}{{\rm{x}}^{\rm{3}}} + {\rm{11}}{{\rm{x}}^{\rm{2}}} - {\rm{10x}} - {\rm{10}}\)  (1 điểm).

Câu 4:        

Ta có \(x = \frac{{{\rm{2}}{\rm{.9}}{\rm{.8}} + {\rm{3}}{\rm{.12}}{\rm{.10}} + {\rm{4}}{\rm{.15}}{\rm{.12}} + ... + {\rm{98}}{\rm{.297}}{\rm{.200}}}}{{{\rm{2}}{\rm{.3}}{\rm{.4}} + {\rm{3}}{\rm{.4}}{\rm{.5}} + {\rm{4}}{\rm{.5}}{\rm{.6}} + ... + {\rm{98}}{\rm{.99}}{\rm{.100}}}}\)

                   \( = \frac{{\left( {{\rm{2}}{\rm{.3}}} \right){\rm{.2}}{\rm{.3}}{\rm{.4}} + \left( {{\rm{2}}{\rm{.3}}} \right){\rm{.3}}{\rm{.4}}{\rm{.5}} + \left( {{\rm{2}}{\rm{.3}}} \right){\rm{.4}}{\rm{.5}}{\rm{.6}} + ...{\rm{ + }}\left( {{\rm{2}}{\rm{.3}}} \right){\rm{.98}}{\rm{.99}}{\rm{.100}}}}{{{\rm{2}}{\rm{.3}}{\rm{.4}} + {\rm{3}}{\rm{.4}}{\rm{.5}} + {\rm{4}}{\rm{.5}}{\rm{.6}} + ... + {\rm{98}}{\rm{.99}}{\rm{.100}}}}\)

                   \( = \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\frac{{{\rm{2}}{\rm{.3}}\left( {{\rm{2}}{\rm{.3}}{\rm{.4}} + {\rm{3}}{\rm{.4}}{\rm{.5}} + {\rm{4}}{\rm{.5}}{\rm{.6}} + ... + {\rm{98}}{\rm{.99}}{\rm{.100}}} \right)}}{{{\rm{2}}{\rm{.3}}{\rm{.4}} + {\rm{3}}{\rm{.4}}{\rm{.5}} + {\rm{4}}{\rm{.5}}{\rm{.6}} + ... + {\rm{98}}{\rm{.99}}{\rm{.100}}}}\)

                   \( = 2.3 = 6\)

          Thay x = 6 vào biểu thức P(x), ta được

:

                   \({\rm{P}}\left( 6 \right){\rm{ =  }}{{\rm{6}}^{\rm{2}}} - {\rm{12}}{\rm{.6}} + {\rm{35}} = {\rm{36}} - {\rm{72}} + {\rm{35}} = {\rm{71}} - {\rm{72}} =  - {\rm{1}} < {\rm{0}}\)

          Vậy x = 6 không là nghiệm của đa thức P(x).    (0,5 điểm)

Câu 5:        

          a) Ta có ΔABC vuông tại A

          \( \Rightarrow {\rm{B}}{{\rm{C}}^{\rm{2}}} = {\rm{A}}{{\rm{B}}^{\rm{2}}} + {\rm{A}}{{\rm{C}}^{\rm{2}}}\) (định lý Pytago)

                \(\begin{array}{l}{\rm{1}}{{\rm{0}}^{\rm{2}}} = {\rm{A}}{{\rm{B}}^{\rm{2}}} + {{\rm{6}}^{\rm{2}}}\\{\rm{100}} = {\rm{A}}{{\rm{B}}^{\rm{2}}} + {\rm{36}}\end{array}\)

          \(\begin{array}{l} \Rightarrow {\rm{A}}{{\rm{B}}^{\rm{2}}} = {\rm{100}} - {\rm{36}} = {\rm{64}}\\ \Rightarrow {\rm{AB}} = \sqrt {{\rm{64}}}  = {\rm{8cm}}\,\,\,\,\,\end{array}\)             (0,5 điểm)

          Ta có \({\rm{BM}} = \frac{{{\rm{AB}}}}{{\rm{2}}} = \frac{{\rm{8}}}{{\rm{2}}} = {\rm{4cm}}\) (vì M là trung điểm của AB)    (0,5 điểm)

b)

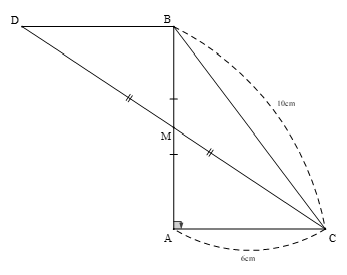
          Xét ΔMAC và ΔMBD có:

                   \(\widehat {{\rm{AMC}}} = \widehat {{\rm{BMD}}}\) (2 góc đối đỉnh)

                   MA = MB (vì M là trung điểm của AB)

                   MC = MD (gt)

          Do đó:  ΔMAC = ΔMBD (c.g.c)

          \( \Rightarrow {\rm{AC}} = {\rm{BD}}\) (2 cạnh tương ứng)        (1 điểm)

c)  Ta có AC + BC = BD + BC (1) (vì AC = BD)

          Lại có 2CM = CD (2) (vì M là trung điểm của CD)         

          Xét ΔBCD có: BD + BC > CD (3) (bất đẳng thức tam giác)

          Từ (1), (2) và (3) \( \Rightarrow \) AC + BC > 2CM         (1 điểm)

d)

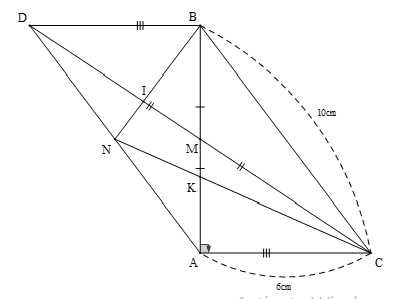
          Xét ΔACD có: AM là đường trung tuyến và \(\frac{{{\rm{AK}}}}{{{\rm{AM}}}} = \frac{{\rm{2}}}{{\rm{3}}}\) (gt)

          \( \Rightarrow \) K là trọng tâm của ΔACD

          \( \Rightarrow \) CK cắt AD tại N là trung điểm của AD

          Xét ΔABD có: DM và BN là 2 đường trung tuyến cắt nhau tại I

          \( \Rightarrow \) I là trọng tâm ΔABD

          \( \Rightarrow {\rm{ID}} = \frac{{\rm{2}}}{{\rm{3}}}{\rm{DM}}\)

                     \( = \frac{{\rm{2}}}{{\rm{3}}}{\rm{.}}\frac{{{\rm{DC}}}}{{\rm{2}}} = \frac{{{\rm{DC}}}}{{\rm{3}}}\) (vì M là trung điểm của DC)

          \( \Rightarrow {\rm{DC}} = {\rm{3ID}}\) (0,5 điểm).

-----------------------

Bộ 21 Đề thi Toán lớp 7 Học kì 2 năm 2024 có đáp án - Đề 13

Phòng Giáo dục và Đào tạo .....

Đề thi Học kì 2 - Năm học 2024 - 2025

Bài thi môn: Toán lớp 7

Thời gian làm bài: 90 phút

(Đề 13)

Câu 1: (1.5 điểm)

     Điểm kiểm tra 1 tiết môn toán của lớp 7A được bạn lớp trưởng ghi lại như sau

5	8	4	8	6	6	5	7	4	3	6	7
7	3	8	6	7	6	5	9	7	9	7	4
4	7	10	6	7	5	4	7	6	5	2	8

 

a) Dấu hiệu ở đây là gì? Số các giá trị là bao nhiêu?

b) Lập bảng “tần số” và tìm Mốt của dấu hiệu;

c) Tính số trung bình cộng của dấu hiệu.

Câu 2: (1 điểm)

 Cho đa thức M = 6x⁶y + \(\frac{1}{3}\)x⁴y³ – y⁷ – 4x⁴y³ + 10 – 5x⁶y + 2y⁷ – 2,5

a) Thu gọn và tìm bậc của đa thức;

b) Tính giá trị của đa thức tại x = –1 và y = 1.

 

Câu 3:  (2.5 điểm)

 Cho hai đa thức:

   P(x) = x² + 5x⁴ – 3x³ + x² + 4x⁴ + 3x³ – x + 5

  Q(x) = x – 5x³ – x² – x⁴ + 4x³ – x² + 3x – 1

a) Thu gọn  rồi sắp xếp các đa thức trên theo luỹ thừa giảm dần của biến;

b) Tính  P(x) + Q(x) và P(x) – Q(x).

 

  

Câu 4: (1 điểm)

Tìm nghiệm của các đa thức  

 a) R(x) = 2x + 3;            b)  H(x) = (x – 1)(x + 1).

Câu 5: (3 điểm)

 Cho \(\Delta \)ABC cân tại A (\(\widehat A\) nhọn ). Tia phân giác góc của A cắt BC tại I.

 a) Chứng minh AI \( \bot \) BC;

 b) Gọi D là trung điểm của AC, M là giao điểm của BD với AI. Chứng minh rằng M là trọng tâm của tâm giác ABC;

 c) Biết AB = AC = 5cm; BC = 6 cm. Tính AM.

Câu 6: (1 điểm)

 Trên tia phân giác góc A của tam giác ABC (AB > AC) lấy điểm M.

 Chứng minh \(\left| {MB - MC} \right| < AB - AC\).

-----------HẾT-----------

Đáp án và hướng dẫn giải

Câu 1:

a) Dấu hiệu ở đây là điểm kiểm tra toán một tiết của mỗi học sinh

Số các giá trị là: N = 36             (0,5 điểm)

b) Bảng tần số:

Giá trị (x)	2	3	4	5	6	7	8	9	10
Tần số (n)	1	2	5	5	7	9	4	2	1	N = 36

 Mốt của dấu hiệu là: M₀ = 7               (0,5 điểm)

 c) Số trung bình cộng của dấu hiệu là:

  \(\overline X  = \frac{{(2 + 3.2 + 4.5 + 5.5 + 6.7 + 7.9 + 8.4 + 9.2 + 10)}}{{36}} \approx 6,06\) (0,5 điểm)

Câu 2:

 a) M = 6x⁶y + \(\frac{1}{3}\)x⁴y³ – y⁷ – 4x⁴y³ + 10 – 5x⁶y + 2y⁷ – 2,5

= \(\left( {6{x^6}y - 5{x^6}y} \right) + \left( {\frac{1}{3}{x^4}{y^3} - 4{x^4}{y^3}} \right) + \left( { - {y^7} + 2{y^7}} \right) + \left( {10 - 2,5} \right)\)

= \({x^6}y - \frac{{11}}{3}{x^4}{y^3} + {y^7} + 7,5\)

= \({y^7} + {x^6}y - \frac{{11}}{3}{x^4}{y^3} + 7,5\)

Hạng tử y⁷ có bậc là 7; hạng tử x⁶y có bậc là 7 và hạng tử \( - \frac{{11}}{3}{x^4}{y^3}\) có bậc là 7 nên đa thức M có bậc là 7.

Vậy M = y⁷ + x⁶y – \(\frac{{11}}{3}\)x⁴y³ + 7,5 và đa thức có bậc 7.  (0,5 điểm)

b) Thay x = –1 và y = 1 vào đa thức M ta được:

 M(–1; 1) = 1⁷ + (–1)⁶.1 – \(\frac{{11}}{3}\)(–1)⁴.1³ + 7,5 = 1 + 1 – \(\frac{{11}}{3}\) + 7,5 = \(\frac{{35}}{6}\)

Vậy M = \(\frac{{35}}{6}\) tại x = –1 và y = 1.      (0,5 điểm)

Câu 3:

a) Thu gọn rồi sắp xếp theo lũy thừa giảm dần của biến:

 P(x) = x² + 5x⁴ – 3x³ + x² + 4x⁴ + 3x³ – x + 5

= \(\left( {5{x^4} + 4{x^4}} \right) + \left( { - 3{x^3} + 3{x^3}} \right) + \left( {{x^2} + {x^2}} \right) - x + 5\)

= 9x⁴ + 2x² – x + 5          (0,5 điểm)

Q(x) = x – 5x³ – x² – x⁴ + 4x³ – x² + 3x – 1

= \( - {x^4} + \left( { - 5{x^3} + 4{x^3}} \right) + \left( { - {x^2} - {x^2}} \right) + \left( {x + 3x} \right) - 1\)

= –x⁴ – x³ – 2x² + 4x – 1           (0,5 điểm)

b) P(x) + Q(x) = (9x⁴ + 2x² – x + 5) + (–x⁴ – x³ – 2x² + 4x – 1)

= \(9{x^4} + 2{x^2} - x + 5 - {x^4} - {x^3} - 2{x^2} + 4x - 1\)

= \(\left( {9{x^4} - {x^4}} \right) - {x^3} + \left( {2{x^2} - 2{x^2}} \right) + \left( { - x + 4x} \right) + \left( {5 - 1} \right)\)

= 8x⁴ – x³ + 3x + 4                    (1 điểm)

P(x) – Q(x) = (9x⁴ + 2x² – x + 5) – (–x⁴ – x³ – 2x² + 4x – 1)

= \(9{x^4} + 2{x^2} - x + 5 + {x^4} + {x^3} + 2{x^2} - 4x + 1\)

= \(\left( {9{x^4} + {x^4}} \right) + {x^3} + \left( {2{x^2} + 2{x^2}} \right) + \left( { - x - 4x} \right) + \left( {5 + 1} \right)\)

= 10x⁴ + x³ + 4x² – 5x + 6                  (0,5 điểm)

Câu 4: Tìm được nghiệm của đa thức

a) R(x) = 2x + 3

Ta có: R(x) = 0 hay 2x + 3 = 0 \( \Rightarrow x =  - \frac{3}{2}\)

Vậy nghiệm của đa thức R(x) là x = \( - \frac{3}{2}\).     (0,5 điểm)

b. H(x) = (x – 1)(x + 1)  

Ta có: H(x) = 0 hay (x – 1)(x + 1) = 0

Suy ra x – 1 = 0 hoặc x + 1 = 0

Suy ra x = 1 hoặc x = –1

Vậy nghiệm của đa thức H(x) là x = 1; x = –1.        (0,5 điểm)

Câu 5:

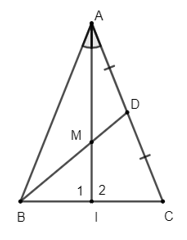
Vẽ hình đúng và ghi GT, KL đúng. (0,5 điểm)

a) Xét tam giác AIB và tam giác AIC có:

AB = AC (tam giác ABC cân tại A)

AI: cạnh chung

\(\widehat {BAI} = \widehat {CAI}\) (AI là tia phân giác của góc A)

Do đó: \(\Delta \)AIB = \(\Delta \)AIC (cgc) \( \Rightarrow {\widehat I_1} = {\rm{ }}{\widehat I_2}\) (Hai góc tương ứng)

 Mà \[{\widehat I_1} + {\rm{ }}{\widehat I_2} = {\rm{ }}180^\circ \](Hai góc kề bù) \( \Rightarrow \)\[{\widehat I_1} = \;{\widehat I_2}\; = {90^0}\; \Rightarrow \;AI\;\; \bot \;BC\].  (1 điểm)

b) Ta có  DA = DC (D là trung điểm của AC)

Nên BD là đường trung tuyến ứng với cạnh AC.

Trong tam giác cân ABC (cân tại A), AI là đường phân giác ứng với đáy BC

Suy ra AI cũng là đường trung tuyến

Do đó M là giao của hai đường trung tuyến AI và BD nên M là trọng tâm của tam giác ABC (Tính chất ba đường trung tuyến của tam giác)  (1 điểm)

c) Trong tam giác cân ABC (cân tại A), AI là phân giác cũng là trung tuyến

Nên I là trung điểm của BC

\( \Rightarrow \) IB = IC = \(\frac{1}{2}\)BC

\( \Rightarrow \) IB = IC = \(\frac{1}{2}.6\) = 3 (cm)

Áp dụng định lí Py-ta-go vào tam giác vuông AIB, ta có:

AI² = AB² – IB² = 5² – 3² = 16

 AI = 4 (cm)

M là trọng tâm của tam giác ABC   AM = AI = . 4 =   (cm)   (0,5 điểm)

Câu 6:

\( \Rightarrow \)

-  Kẻ MI vuông góc với AB tại I; MJ vuông góc với AC tại J \( \Rightarrow \) MI = MJ (1) (Tính chất tia phân giác của góc)

- Ta lại có AB – AC = AI + IB – (AJ + JC) \( \Rightarrow \)AB – AC = IB – JC (2) (Hai tam giác vuông AIM và AJM bằng nhau (cạnh huyền, góc nhọn) \( \Rightarrow \) AI = AJ).

- Trên tia IB lấy điểm C’ sao cho IC’ = JC. Từ (2) suy ra AB – AC = IB – IC’ = C’B (3)

Trong tam giác BMC’, ta có C’B > |MB – MC’| (BĐT tam giác)    (4)

- Măt khác ta có \(\Delta \)MIC’ = \(\Delta \)MJC (c.g.c) \( \Rightarrow \) MC’ = MC (5).

Từ (3), (4) và (5) suy ra AB – AC > |MB – MC|      (đpcm)

-----------------------

 

Bộ 21 Đề thi Toán lớp 7 Học kì 2 năm 2024 có đáp án - Đề 14

Phòng Giáo dục và Đào tạo .....

Đề thi Học kì 2 - Năm học 2024 - 2025

Bài thi môn: Toán lớp 7

Thời gian làm bài: 90 phút

(Đề 14)

Câu 1: (1 điểm)

a)     Bậc của đơn thức là gì?

        b) Thu gọn và tìm bậc đơn thức sau:  –3x²y . 4xy³.\(\)     

Câu 2: (1 điểm)

a) Phát biểu định lý Py–ta–go;

b) Tìm x trên hình vẽ dưới đây.

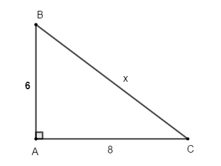
Câu 3: (2 điểm) Thời gian giải xong một bài toán (tính bằng phút) của mỗi học sinh lớp 7 được ghi lại ở bảng sau

10	13	15	10	13	15	17	17	15	13
15	17	15	17	10	17	17	15	13	15

 

       a) Dấu hiệu điều tra ở đây là gì? Có bao nhiêu giá trị của dấu hiệu?

       b) Lập bảng tần số và tính số trung bình cộng của dấu hiệu. \(\)                                

Câu 4: (3 điểm) Cho hai đa thức f(x) = 3x + x³ + 2x² + 4

                                                      g(x) = x³ + 3x + 1 – x²

    a) Sắp xếp các đa thức trên theo lũy thừa giảm dần của biến;

b) Tính f(x) + g(x) và f(x) – g(x);

c) Chứng tỏ f(x) – g(x) không có nghiệm.

Câu 5: (3 điểm)   Cho tam giác ABC cân tại A, đường cao AH. Biết AB = 10cm,

 BC = 12cm.

a) Chứng minh \[\Delta AHB = \Delta AHC\];

b) Tính độ dài đoạn thẳng AH;

     c) Gọi G là trọng tâm của tam giác ABC. Chứng minh ba điểm A, G, H thẳng hàng.

--------------HẾT--------------

Đáp án và hướng dẫn giải

Câu 1:

a) Bậc của đơn thức có hệ số khác 0 là tổng số mũ của tất cả các biến có trong đơn thức đó.  (0,5 điểm)

b) –3x²y . 4xy³ = (–3.4).(x².x).(y.y³) = –12x³y⁴

Bậc của đơn thức –12x³y⁴ là 3 + 4 = 7.   (0,5 điểm)

Câu 2:

a) Định lý Py–ta–go: "Trong một tam giác vuông, bình phương của cạnh huyền bằng tổng các bình phương của hai cạnh góc vuông."  (0,5 điểm)

b)

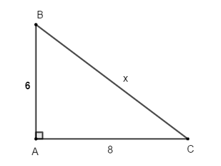
Vì \[\Delta ABC\]vuông tại A nên theo định lý Py–ta–go ta có:

\[B{C^2} = A{B^2} + A{C^2}\]

Hay \[{x^2} = {6^2} + {8^2}\]

\[{x^2} = 36 + 64 = 100\] \[ \Rightarrow x = 10\]

Vậy x = 10.   (0,5 điểm)

Câu 3: (Mỗi ý nhỏ 0,5 điểm)

a) Dấu hiệu ở đây là thời gian làm một bài toán (tính bằng phút) của mỗi học sinh.

    Có 20 giá trị.

b) Bảng “tần số”

Giá trị (x)	10	13	15	17
Tần số (n)	3	4	7	6	N = 20

 

Số trung bình cộng là:  

\(\overline X  = \frac{{10 \cdot 3 + 13 \cdot 4 + 15 \cdot 7 + 17 \cdot 6}}{{20}} = \frac{{289}}{{20}} = 14,45\).

Câu 4:

a)  f(x) = 3x +  x³ + 2x²  + 4 = x³ + 2x² + 3x + 4   (0,5 điểm)

     g(x) = x³  + 3x + 1 – x²  = x³ – x² + 3x + 1   (0,5 điểm)

b) Ta có: f(x) + g(x) = (x³ + 2x² + 3x + 4) + (x³ – x² + 3x + 1)

                        = x³ + 2x² + 3x + 4 + x³ – x² + 3x + 1

                        = (x³ + x³) + (2x² – x²) + (3x + 3x) + (4 + 1)

                        = 2x³ + x² + 6x +5     (0,5 điểm)

 

     f(x) – g(x) = (x³ + 2x² + 3x + 4) – (x³ – x² + 3x + 1)

                      = x³ + 2x² + 3x + 4 – x³ + x² – 3x – 1

              = (x³ – x³) + (2x² + x²) + (3x – 3x) + (4 – 1)

              =   3x² + 3                      (0,5 điểm)

c) Vì 3x² ≥ 0 với mọi x nên 3x² + 3 ≥ 3 với mọi x

Do đó không tìm được giá trị nào của x để 3x² + 3 = 0

Vậy f(x) – g(x) = 3x² + 3 không có nghiệm.        (1 điểm)

Câu 5: Vẽ đúng hình, ghi GT – KL 0,5 điểm

a) Xét  ∆ABH và ∆ACH có

\(\widehat {AHB} = \widehat {AHC} = 90^\circ \) (AH là đường cao của tam giác ABC)

AB = AC (vì ∆ABC cân tại A)

Có cạnh AH chung  

Vậy ∆ABH = ∆ACH (cạnh huyền – cạnh góc vuông)  (1 điểm)

b) Xét ∆ABH có \(\widehat {AHB} = 90^\circ \) ,

AB = 10cm, \(BH = \frac{{BC}}{2} = \frac{{12}}{2} = 6\)

Áp dụng định lý Py–ta–go ta có:

\(\begin{array}{l}A{H^2} = A{B^2} - B{H^2} = {10^2} - {6^2}\\ = 100 - 36 = 64\\ \Rightarrow AH = 8cm\end{array}\)            (1 điểm)

c) ∆ABC cân tại A nên đường cao AH cũng đồng thời là đường trung tuyến từ A mà G là trọng tâm ∆ABC lên G thuộc AH hay 3 điểm A, G, H thẳng hàng. (0,5 điểm)

-----------------------

 

Bộ 21 Đề thi Toán lớp 7 Học kì 2 năm 2024 có đáp án - Đề 15

Phòng Giáo dục và Đào tạo .....

Đề thi Học kì 2 - Năm học 2024 - 2025

Bài thi môn: Toán lớp 7

Thời gian làm bài: 90 phút

(Đề 15)

Câu 1: (1.5 điểm)

         Thời gian (Tính bằng phút) giải một bài toán của học sinh lớp 7A được thầy giáo bộ môn ghi lại như sau

 

4	8	4	8	6	6	5	7	5	3	6	7
7	3	6	5	6	6	6	9	7	9	7	4
4	7	10	6	7	5	4	6	6	5	4	8

 

a) Dấu hiệu ở đây là gì ? Số các giá trị là bao nhiêu ?

b) Lập bảng “tần số” và tìm Mốt của dấu hiệu ;

c) Tính số trung bình cộng của dấu hiệu.

 

Câu 2 : (1 điểm)

 Cho đa thức M = 3x⁶y + \(\frac{1}{2}\)x⁴y³ – 4y⁷ – 4x⁴y³ + 11 – 5x⁶y + 2y⁷ – 2.

a) Thu gọn và tìm bậc của đa thức ;

b) Tính giá trị của đa thức tại x = 1 và y = –1.

Câu 3 :  (2.5 điểm)

 Cho hai đa thức :

  R(x) = x² + 5x⁴ – 2x³ + x² + 6x⁴ + 3x³ – x + 15

  H(x) = 2x – 5x³ –  x² – 2x⁴ + 4x³ – x² + 3x – 7

a) Thu gọn  rồi sắp xếp các đa thức trên theo luỹ thừa giảm dần của biến;

b) Tính  R(x) + H(x)  và R(x) – H(x).  

Câu 4: (1 điểm)

Tìm nghiệm của các đa thức  

 a) P(x) = 5x – 3;             b)  F(x) = (x + 2)(x – 1).

Câu 5: (3 điểm)

 Cho \(\Delta \)ABC cân tại A (\(\widehat A\) nhọn ). Tia phân giác góc của A cắt BC tại I.

 a) Chứng minh AI \( \bot \) BC;

 b) Gọi M là trung điểm của AB, G là giao điểm của CM với AI. Chứng minh rằng BG là đường trung tuyến của tam giác ABC;

 c) Biết AB = AC = 15cm; BC = 18 cm. Tính GI.

Câu 6: (1 điểm)

 Cho đoạn thẳng AB. Gọi d là đường trung trực của AB. Trên đường thẳng d lấy điểm M bất kì. Trong mặt phẳng lấy đểm C sao cho BC < CA.

a) So sánh MB + MC với CA;

b) Tìm vị trí của M trên d sao cho MB + MC nhỏ nhất.

 

-----------HẾT-----------

Đáp án và hướng dẫn giải

Câu 1:

a) Dấu hiệu ở đây là thời gian (tính bằng phút) giải một bài toán toán của mỗi học sinh.

Số các giá trị là: N = 36.           (0,5 điểm)

b) Bảng tần số:

Giá trị (x)	3	4	5	6	7	8	9	10
Tần số (n)	2	6	5	10	7	3	2	1	N = 36

 

Mốt của dấu hiệu là: M₀ = 6.               (0,5 điểm)

 c) Số trung bình cộng của dấu hiệu là:

 \(\overline X  = \frac{{(3.2 + 4.6 + 5.5 + 6.10 + 7.7 + 8.3 + 9.2 + 10)}}{{36}} = 6\).                 (0,5 điểm)

Câu 2:

a) Ta có

M = 3x⁶y + \(\frac{1}{2}\)x⁴y³ – 4y⁷ – 4x⁴y³ + 11 – 5x⁶y + 2y⁷ – 2

= \(\left( {3{x^6}y - 5{x^6}y} \right) + \left( {\frac{1}{2}{x^4}{y^3} - 4{x^4}{y^3}} \right) + \left( { - 4{y^7} + 2{y^7}} \right) + \left( {11 - 2} \right)\)

= \( - 2{x^6}y - \frac{7}{2}{x^4}{y^3} - 2{y^7} + 9\)

= \( - 2{y^7} - 2{x^6}y - \frac{7}{2}{x^4}{y^3} + 9\)

Vậy M = –2y⁷ – 2x⁶y –\(\frac{7}{2}\)x⁴y³ + 9 và đa thức có bậc 7.      (0,5 điểm)

b) Thay x = 1 và y = –1 vào đa thức ta được:

 M(1; –1) = –2.1⁷ – 2.1⁶.( –1) – \(\frac{7}{2}\).1⁴.( –1)³ + 9 = –2 + 2 +\(\frac{7}{2}\)+ 9  = 12,5. (0,5 điểm)

Câu 3:

a) Thu gọn rồi sắp xếp theo lũy thừa giảm dần của biến, ta được:

R(x) = x² + 5x⁴ – 2x³ + x² + 6x⁴ + 3x³ – x + 15

= \(\left( {5{x^4} + 6{x^4}} \right) + \left( {3{x^3} - 2{x^3}} \right) + \left( {{x^2} + {x^2}} \right) - x + 15\)

= \(11{x^4} + {x^3} + 2{x^2} - x + 15\)      (0,5 điểm)

 

H(x) = 2x – 5x³ – x² – 2x⁴ + 4x³ – x² + 3x – 7

= \( - 2{x^4} + \left( { - 5{x^3} + 4{x^3}} \right) + \left( { - {x^2} - {x^2}} \right) + \left( {2x + 3x} \right) - 7\)

= –2x⁴ – x³ – 2x² + 5x – 7         (0,5 điểm)

b) Ta có:

R(x) + H(x) = \(\left( {11{x^4} + {x^3} + 2{x^2} - x + 15} \right)\)+ (–2x⁴ – x³ – 2x² + 5x – 7)

= \(11{x^4} + {x^3} + 2{x^2} - x + 15 - 2{x^4} - {x^3} - 2{x^2} + 5x - 7\)

= \(\left( {11{x^4} - 2{x^4}} \right) + \left( {{x^3} - {x^3}} \right) + \left( {2{x^2} - 2{x^2}} \right) + \left( { - x + 5x} \right) + \left( {15 - 7} \right)\)

= 9x⁴ + 4x + 8                 (1 điểm)

R(x) – H(x) = \(\left( {11{x^4} + {x^3} + 2{x^2} - x + 15} \right)\)– (–2x⁴ – x³ – 2x² + 5x – 7)

= \(11{x^4} + {x^3} + 2{x^2} - x + 15 + 2{x^4} + {x^3} + 2{x^2} - 5x + 7\)

= \(\left( {11{x^4} + 2{x^4}} \right) + \left( {{x^3} + {x^3}} \right) + \left( {2{x^2} + 2{x^2}} \right) + \left( { - x - 5x} \right) + \left( {15 + 7} \right)\)

= 13x⁴ + 2x³ + 4x² – 6x + 22     (0,5 điểm)

Câu 4:

a) P(x) = 5x – 3 có nghiệm \( \Leftrightarrow \)  5x – 3 = 0 \( \Leftrightarrow \) x = \(\frac{3}{5}\)     (0,5 điểm)   

b) F(x) = (x + 2)(x – 1) có nghiệm \( \Leftrightarrow \) (x + 2)(x – 1) = 0

\( \Leftrightarrow \) x + 2 = 0 hoặc x – 1 = 0 \( \Leftrightarrow \) x = –2 hoặc x = 1 (0,5 điểm)

Câu 5:

- Vẽ hình đúng và ghi GT, KL đúng. (0,5 điểm)

a) Xét tam giác AIB và tam giác AIC có:

AB = AC (tam giác ABC cân tại A)

AI là cạnh chung

\(\widehat {BAI} = \widehat {CAI}\)(AI là tia phân giác của góc A)

 Do đó: \(\Delta \)AIB = \(\Delta \)AIC (cgc) \( \Rightarrow {\widehat I_1} = {\rm{ }}{\widehat I_2}\) (Hai góc tương ứng)

 Mà \[{\widehat I_1} + {\rm{ }}{\widehat I_2} = {\rm{ }}180^\circ \](Hai góc kề bù) \( \Rightarrow \)\[{\widehat I_1} = \;{\widehat I_2}\; = {90^0}\; \Rightarrow \;AI\;\; \bot \;BC\].  (1 điểm)

b) Ta có:  MA = MB (M là trung điểm của AB)

 \( \Rightarrow \) CM là đường trung tuyến ứng với cạnh AB.

Trong tam giác cân ABC (cân tại A), AI là đường phân giác ứng với đáy BC

\( \Rightarrow \) AI cũng là đường trung tuyến

Do đó G  là  giao của hai trung tuyến AI và CM nên G là trọng tâm của tam giác ABC (Tính chất ba đường trung tuyến của tam giác)

Nên BG là đường trung tuyến của tam giác ABC.    (1 điểm)

c) Trong tam giác cân ABC (Cân tại A), AI là phân giác cũng là trung tuyến

Nên IB = IC = \(\frac{1}{2}\)BC  \( \Rightarrow \) IB = IC = 9 (cm)

Áp dụng định lí Py–ta–go vào tam giác vuông AIB, ta có:

AI² = AB² – IB² = 15² – 9² = 144 \( \Rightarrow \) AI =  12 (cm)

G là trọng tâm của tam giác ABC \( \Rightarrow \) GI = \(\frac{1}{3}\)AI = \(\frac{1}{3}\). 12 =  4 (cm)       (0,5 điểm)                              

Câu 6:

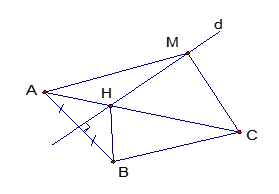
a) M thuộc đường trung trực d của AB nên MA = MB (tính chất đường trung trực của đoạn thẳng)

Suy ra MB + MC = MA + MC.

Trong tam giác MAC, ta có: MA + MC > AC.

Vậy MB + MC > AC   (0,5 điểm)

 b) Vì CB < CA nên C và B nằm trong cùng một nửa mặt phẳng bờ d.

Nên A và C nằm trong hai nửa  mặt phẳng bờ d khác nhau.

Do đó d cắt AC tại H.

Vậy khi M \( \equiv \) H thì: MB + MC = HB + HC = HA + HC

                                 \( \Rightarrow \) MB + MC = AC

Vậy ta có MB + MC \( \ge \) AC

Khi M trùng với H  thì HB + HC = AC.

Tức là  MB + MC nhỏ nhất khi M \( \equiv \) H là giao điểm của AC với d.  (0,5 điểm)

-----------------------