Tài liệu Bộ đề thi Toán lớp 9 học kì 2 có đáp án năm học 2023 - 2024 gồm 20 đề thi tổng hợp từ đề thi môn Toán 9 của các trường THCS trên cả nước đã được biên soạn đáp án chi tiết giúp học sinh ôn luyện để đạt điểm cao trong bài thi học kì 2 Toán lớp 9. Mời các bạn cùng đón xem:
Chỉ từ 150k mua trọn bộ Đề thi học kì 2 Toán 9 bản word có lời giải chi tiết:
B1: Gửi phí vào tài khoản 0711000255837 - NGUYEN THANH TUYEN - Ngân hàng Vietcombank
B2: Nhắn tin tới zalo Vietjack Official - nhấn vào đây để thông báo và nhận giáo án.
Xem thử tài liệu tại đây: Link tài liệu
Đề thi Toán 9 Học kì 2 năm 2024 có đáp án (20 đề) - Đề 1
Phòng Giáo dục và Đào tạo .....
Đề thi Học kì 2
Môn: Toán lớp 9
Thời gian làm bài: 90 phút
(Đề 1)
Câu 1: Phương trình nào sau đây là phương trình bậc nhất hai ẩn:
A. 2x2 - 3x + 1 = 0 B.-2x = 4
C. 2x + 3y = 7 D. 1/x + y = 3
Câu 2: Hệ phương trình 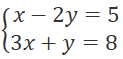
A. (-3; -1) B. (3; 1)
C. (3; -1) D. (1; -3)
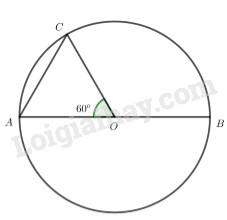
Câu 3: Cho AB là dây cung của đường tròn (O; 4 cm), biết AB = 4 cm, số đo của cung nhỏ AB là:
A. 60o B. 120o C. 30o D. 90o
Câu 4: Bán kính hình tròn nội tiếp hình vuông cạnh 2 cm là:
A.2 cm B.√2 cm C.1 cm D.4 cm
Bài 1 (1, 5 điểm) giải phương trình và hệ phương trình sau:
a) x2 - 7x + 5 = 0
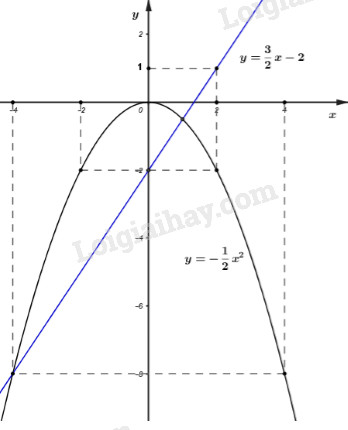
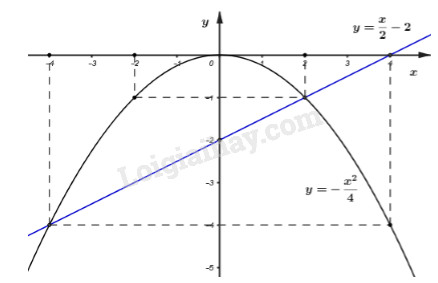
Bài 2 (1, 5 điểm) Cho hai hàm số : y = x2 (P) và y = - x + 2 (d)
a) Vẽ 2 đồ thì hàm số trên cùng 1 hệ trục tọa độ
b) Tìm tọa độ giao điểm của (P) và (d)
c) Viết phương trình đường thẳng d' song song với d và cắt (P) tại điểm có hoành độ -1.
Bài 3 (1, 5 điểm) Cho phương trình x2 + (m – 2)x – m + 1 =0
a) Tìm m để phương trình có 1 nghiệm x = 2. Tìm nghiệm còn lại
b) Chứng minh rằng phương trình luôn có nghiệm với mọi m
c) Tìm giá trị nhỏ nhất của biểu thức A = x12 + x22 -6x1 x2
Bài 4 (3,5 điểm) Cho (O;OA), dây BC vuông góc với OA tại K. Kẻ tiếp tuyến của (O) tại B và A, hai tiếp tuyến này cắt nhau tại H
a) Chứng minh tứ giác OBHA nội tiếp được đường tròn
b) Lấy trên O điểm M (M khác phía với A so với dây BC, dây BM lớn hơn dây MC). Tia MA và BH cắt nhau tại N. chứng minh ∠(NMC) = ∠(BAH)
c) Tia MC và BA cắt nhau tại D. Chứng minh tứ giác MBND nội tiếp được đường tròn.
d) Chứng minh OA ⊥ ND
Hướng dẫn giải
| 1.C | 2.C | 3.A | 4.B |
Câu 4: Chọn đáp án C
Kẻ OH ⊥ AB. Do ABCD là hình vuông nên ∠OAH = 45o
Tam giác ABC vuông tại B có: AC2 = AB2 + BC2 = 22 + 22 = 8
Nên AC = 2√2cm
Vì O là trung điểm AC nên
Xét tam giác OAH vuông tại H có:
Vậy bán kính đường tròn nội tiếp hình vuông cạnh 2cm là 1cm
Bài 1
a) x2 - 7x + 5 = 0
Δ = 72 - 4.1.5 = 49 - 20 = 29 > 0
⇒ Phương trình đã cho có 2 nghiệm phân biệt
Vậy hệ phương trình đã cho có tập nghiệm
Vậy hệ phương trình đã cho có nghiệm (x; y) = (0; 3)
Bài 2
a) Xét hàm số: y = x2 (P)
Tập xác định R
Bảng giá trị
| x | - 2 | - 1 | 0 | 1 | 2 |
| y = x2 | 4 | 1 | 0 | 1 | 2 |
Đồ thị hàm số y = x2 là đường parabol nằm phía trên trục hoành, nhận trục Oy làm trục đối xứng và điểm O(0;0) là đỉnh và là điểm thấp nhất.
Xét hàm số: y = - x + 2 (d)
Tập xác định R
Bảng giá trị
| x | 0 | 2 |
| y = - x + 2 | 2 | 0 |
b) Phương trình hoành độ giao điểm của (P) và (d) là:
x2 = -x + 2 ⇔ x2 + x - 2 = 0
⇒ Phương trình có nghiệm 1 và -2 ( phương trình dạng a + b + c = 0)
Với x = 1 ⇒ y = x2 = 1
Với x = - 2 ⇒ y = x2 = 4
Vậy tọa độ giao điểm của (P) và (d) là (1; 1) và (-2; 4)
c) Do d' // d nên phương trình của d' có dạng: y = -x + b (b ≠ 2)
Gọi A là giao điểm của d' và (P). A có hoành độ -1 ⇒ tung độ của A là 1
Do A (-1; 1) nên tọa độ của A thỏa mãn phương trình đường thẳng d'
⇒ 1 = -(-1) + b ⇒ b = 0
⇒ Phương trình đường thẳng d' là y = -x.
Bài 3 x2 + (m – 2)x – m + 1 = 0
a) phương trình có 1 nghiệm x = 2 nên :
22 + (m-2).2 - m + 1 = 0
⇔ m = -1
Với m = -1, phương trình trở thành: x2 – 3x + 2 = 0
Theo hệ thức Vi-et ta có: x1 + x2 = 3
Giả sử x1 = 2 ⇒ x2 = 1
Vậy với m = - 1 thì phương trình có 1 nghiệm là 2 và nghiệm còn lại là 1.
b) Δ = (m - 2)2 -4.(-m + 1) = m2 - 4m + 4 + 4m - 4 = m2 ≥ 0 ∀ m
⇒ Phương trình đã cho luôn có nghiệm với mọi m
c) Theo hệ thức Vi- et ta có:
A = x12 + x22 -6x1 x2 = (x1 + x2 )2 - 8x1 x2
= (2 - m)2 - 8(-m + 1) = m2 - 4m + 4 + 8m - 8
= m2 + 4m - 4 = (m + 2)2 - 8
Ta có: (m + 2)2 ≥ 0 ∀ m
⇒ (m + 2)2 - 8 ≥ -8 ∀ m ⇔ A ≥ -8 ∀ m
Dấu bằng xảy ra khi (m + 2)2 = 0 ⇔ m= -2
Vậy GTNN của A là -8, đạt được khi m = -2
Bài 4
a) Xét tứ giác OBHA có:
∠(OBH) = 90o ( BH là tiếp tuyến của (O)
∠(OAH) = 90o (AH là tiếp tuyến của (O)
⇒ ∠(OBH) + ∠(OAH) = 180o
⇒ Tứ giác OBHA là tứ giác nội tiếp
b) Ta có: Một phần đường kính OA vuông góc dây BC
⇒ AB = AC ⇒ sđ cung AB = sđ cung AC
⇒ ∠(BAH) = ∠(ABC) (góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung chắn 2 cung bằng nhau)
Tứ giác ABMC nội tiếp (O)
⇒ ∠(NMC) = ∠(ABC) (2 góc nội tiếp cùng chắn cung AC)
Do đó: ∠(NMC) = ∠(BAH)
c) 2 tiếp tuyến HA và HB cắt nhau tại H
⇒ ΔHAB cân tại H ⇒ ∠(BAH) = ∠(HBA)
Theo ý b) ∠(NMC) = ∠(BAH)
⇒ ∠(NMC) = ∠(HBA)
Xét tứ giác MBND có: ∠(NMC) = ∠(HBA)
⇒ 2 đỉnh M và B cùng nhìn cạnh ND dưới 1 góc bằng nhau
⇒ MBND là tứ giác nội tiếp.
d) Xét tứ giác MBND nội tiếp có:
∠(BDN) = ∠(BMN) (2 góc nội tiếp cùng chắn cung BN)
Xét tứ giác ABMC nội tiếp (O) có:
∠(ABC) = ∠(BMN) (2 góc nội tiếp cùng chắn cung bằng nhau )
⇒ ∠(BDN) = ∠(ABC)
Mà 2 góc này ở vị trí so le trong
⇒ ND // BC
Mà BC ⊥ OA ⇒ ND ⊥ OA

..................................................................................
Đề thi Toán 9 Học kì 2 năm 2024 có đáp án (20 đề) - Đề 2
Phòng Giáo dục và Đào tạo .....
Đề thi Học kì 2
Môn: Toán lớp 9
Thời gian làm bài: 90 phút
(Đề 2)
Bài 1: (1,5 điểm) Giải các phương trình và hệ phương trình sau:
a) 3x2 – 7x + 2 = 0
b) x4 – 5x + 4 = 0
Bài 2: (1,5 điểm)
a) Vẽ đồ thị (P) hàm số y= x2/4
b) Trên (P) lấy 2 điểm A và B có hoành độ lần lượt là 4 và 2. Viết phương trình đường thẳng đi qua A và B
Bài 3: (1,5 điểm) Cho phương trình (ẩn x) : x2 – 2mx – 4m – 4 = 0(1)
a) Chứng tỏ phương trình (1) có nghiệm với mọi Giá trị của m.
b) Tìm m để phương trình (1) có 2 nghiệm x1, x2 thỏa mãn x12 + x22 - x1x2 = 13
Bài 4: (1 điểm) Tìm kích thước của hình chữ nhật, biết chiều dài hơn chiều rộng 3m. Nếu tăng thêm mỗi chiều thêm 2 mét thì diện tích của hình chữ nhật tăng thêm 70m2.
Bài 5: (3,5 điểm) Cho đường tròn (O;R) và một điểm A ngoài đường tròn (O) sao cho OA = 3R. Từ A vẽ hai tiếp tuyến AB, AC với (O) (B, C là các tiếp điểm).
a) Chứng minh tứ giác OBAC nội tiếp và OA vuông góc với BC
b) Từ B vẽ đường thẳng song song với AC cắt đường tròn tâm (O) tại D (D khác B), AD cắt đường tròn (O) tại E (E khác D). Tính tích AD.AE theo R.
c) Tia BE cắt AC tại F. Chứng minh F là trung điểm AC.
d) Tính theo R diện tích tam giác BDC.
Đáp án và Hướng dẫn giải
Bài 1:
a) 3x2 – 7x + 2 = 0
Δ= 72 -4.3.2 = 49 - 24 = 25 > 0 ⇒ √Δ = 5
Phương trình có 2 nghiệm phân biệt:
Vậy tập nghiệm của phương trình là S = {2; 1/3}
b) x4 - 5x2 + 4 = 0
Đặt t = x2 ≥ 0 , ta có phương trình:
t2 - 5t + 4 = 0 (dạng a + b + c = 1 -5 + 4 = 0)
t1 = 1 (nhận) ; t2 = 4 (nhận)
với t = 1 ⇔ x2 = 1 ⇔ x = ± 1
với t = 4 ⇔ x2 = 4 ⇔ x = ± 2
Vậy nghiệm của phương trình x = ±1; x = ± 2
Vậy hệ phương trình có nghiệm (x; y) = ( √5; -1)
Bài 2:
a) Tập xác định của hàm số: R
Bảng giá trị:
| x | -4 | -2 | 0 | 2 | 4 |
| y = x2 / 4 | 4 | 1 | 0 | 1 | 4 |
Đồ thị hàm số y = x2 / 4 là một đường parabol nằm phía trên trục hoành, nhận trục Oy làm trục đối xứng và điểm O(0;0) là đỉnh và là điểm thấp nhất.
b) Với x = 4, ta có: y = x2/4 = 4 ⇒ A (4; 4)
Với x = 2, ta có y = x2/4 = 1 ⇒ B ( 2; 1)
Giả sử đường thẳng đi qua 2 điểm A, B là y = ax + b
Đường thẳng đi qua A (4; 4) nên 4 = 4a + b
Đường thẳng đi qua B (2; 1) nên : 1= 2a + b
Ta có hệ phương trình
Vậy phương trình đường thẳng đi qua 2 điểm A, B là y = 3/2 x - 2
Bài 3:
a) Δ' = m2 - (-4m - 4) = m2 + 4m + 4 = (m + 2)2 ≥ 0 ∀m
Vậy phương trình đã cho luôn có nghiệm với mọi m
b) Gọi x1 ; x2 lần lượt là 2 nghiệm của phương trình đã cho
Theo hệ thức Vi-et ta có:
x12 + x22 -x1 x2 = (x1 + x2 )2 - 3x1 x2 = 4m2 + 3(4m + 4)
Theo bài ra: x12 + x22 - x1 x2=13
⇒ 4m2 + 3(4m + 4) = 13 ⇔ 4m2 + 12m - 1 = 0
Δm = 122 -4.4.(-1) = 160 ⇒ √(Δm ) = 4√10
Phương trình có 2 nghiệm phân biệt
Vậy với thì phương trình có 2 nghiệm x1; x2 thỏa mãn điều kiện x12 + x22 - x1 x2 = 13
Bài 4:
Gọi chiều rộng của hình chữ nhật là x (m) ( x > 0 )
⇒ Chiều dài của hình chữ nhật là x + 3 (m)
Khi đó diện tích của hình chữ nhật là x(x + 3) (m2 )
Nếu tăng thêm mỗi chiều thêm 2 mét thì diện tích của hình chữ nhật tăng thêm 70m2 nên ta có phương trình:
(x + 2)(x + 3 + 2) = x(x + 3) + 70
⇔ (x + 2)(x + 5) = x(x + 3) + 70
⇔ x2 + 7x + 10 = x2 + 3x + 70
⇔ 4x = 60
⇔ x = 15
Vậy chiều rộng của hình chữ nhật là 15m
Chiều dài của hình chữ nhật là 18m
Bài 5:
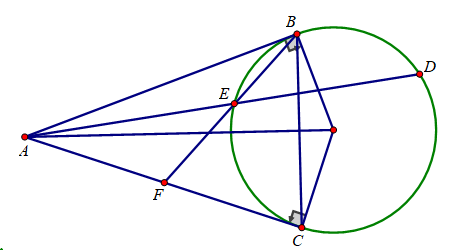


...................................................................................
Đề thi Toán 9 Học kì 2 năm 2024 có đáp án (20 đề) - Đề 3
Phòng Giáo dục và Đào tạo .....
Đề thi Học kì 2
Môn: Toán lớp 9
Thời gian làm bài: 90 phút
(Đề 3)
Câu 1: Cho hàm số y = -3x2. Kết luận nào sau đây là đúng :
A. Hàm số trên luôn đồng biến
B. Hàm số trên luôn nghịch biến
C. Hàm số trên đồng biến khi x > 0, nghịch biến khi x < 0
D. Hàm số trên đồng biến khi x < 0, nghịch biến khi x > 0
Câu 2: Cho phương trình bậc hai x2 – 2(m + 1) x + 4m = 0. Phương trình có nghiệm kép khi m bằng:
A. 1 C. Với mọi m
B. –1 D. Một kết quả khác
Câu 3: Cung AB của đường tròn (O; R) có số đo là 60o. Khi đó diện tích hình quạt AOB là:
Câu 4: Tứ giác MNPQ nội tiếp đường tròn khi:
A.∠(MNP) + ∠(NPQ) = 180o
B.∠(MNP) = ∠(MPQ)
C. MNPQ là hình thang cân
D. MNPQ là hình thoi
Bài 1 (2,0 điểm)
1) Tìm điều kiện xác định của biểu thức
2) Cho biểu thức 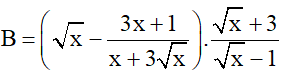
a) Rút gọn biểu thức B
b) Tìm giá trị nhỏ nhất của P = A.B với x > 1
Bài 2 (1,5 điểm) Giải bài toán bằng cách lập phương trình hoặc hệ phương trình
Một tấm bìa hình chữ nhật có chiều dài hơn chiều rộng 3dm. Nếu giảm chiều rộng đi 1dm và tăng chiều dài thêm 1dm thì diện tích tấm bìa là 66 Tính chiều rộng và chiều dài của tấm bìa lúc ban đầu.
Bài 3 (2,0 điểm)
1) Cho phương trình x4 + mx2 - m - 1 = 0(m là tham số)
a) Giải phương trình khi m = 2
b) Tìm giá trị của m để phương trình có 4 nghiệm phân biệt.
2) Trong mặt phẳng tọa độ Oxy cho parabol (P): y = x2 và đường thẳng (d): y = 2x + m (m là tham số).
a) Xác định m để đường thẳng (d) tiếp xúc với parabol (P). Tìm hoành độ tiếp điểm.
b) Tìm giá trị của m để đường thẳng (d) cắt parabol (P) tại hai điểm A, B nằm về hai phía của trục tung, sao cho diện tích có diện tích gấp hai lần diện tích (M là giao điểm của đường thẳng d với trục tung).
Bài 4 (3,5 điểm) Cho đường tròn (O; R), dây AB. Trên cung lớn AB lấy điểm C sao cho A < CB. Các đường cao AE và BF của tam giác ABC cắt nhau tại I.
a) Chứng minh tứ giác AFEB là tứ giác nội tiếp
b) Chứng minh CF.CB = CE.CA
c) Nếu dây AB có độ dài bằng R√3 , hãy tính số đo của (ACB)
d) Đường tròn ngoại tiếp tam giác CEF cắt đường tròn (O; R) tại điểm thứ hai là K (K khác C). Vẽ đường kính CD của (O; R). Gọi P là trung điểm của AB. Chứng minh rằng ba điểm K, P, D thẳng hàng.
Hướng dẫn giải
| 1.D | 2.A | 3.B | 4.C |
Bài 1
Biểu thức A xác định khi √x - 1 ≠ 0 ⇔ √x ≠ 1 ⇔ x ≠ 1
Vậy GTNN của P là 2√3 + 3 đạt được khi x = 4 + 2√3
Bài 2
Gọi chiều dài của tấm bìa là x (x > 3) (dm)
⇒ Chiều rộng của tấm bìa là x – 3 (dm)
Nếu tăng chiều dài 1 dm và giảm chiều rộng 1 dm thì diện tích là 66 dm2 nên ta có phương trình:
(x + 1)(x – 3 – 1) = 66
⇔ (x + 1)(x – 4 ) = 66
⇔ x2 – 3x – 4 – 66 = 0
⇔ x2 – 3x – 70 = 0
Δ = 32 - 4.(-70) = 289 ⇒ √Δ = 17
⇒ Phương trình đã cho có 2 nghiệm
Do x > 3 nên x =10
Vậy chiều dài của tấm bìa là 10 dm
Chiều rộng của tấm bìa là 7 dm.
Bài 3
1) x4 + mx2 - m - 1 = 0
a) Khi m = 2, phương trình trở thành: x4 + 2x2 – 3 = 0
Đặt x2 = t (t ≥ 0). Khi đó ta có phương trình: t2 + 2t - 3 = 0
⇒ Phương trình có nghiệm t = 1 và t = -3 (do phương trình có dạng a + b + c = 0)
Do t ≥ 0 nên t = 1 ⇒ x2 = 1 ⇒ x = ±1
b) Đặt x2 = t (t ≥ 0). Khi đó ta có phương trình: t2 – mt – m – 1 = 0 (*)
Δ = m2 - 4(-m - 1) = m2 + 4m + 4 = (m + 2)2
Phương trình đã cho có 4 nghiệm phân biệt khi và chỉ khi phương trình (*) có 2 nghiệm dương phân biệt
2) parabol (P): y = x2 ; đường thẳng (d): y = 2x + m (m là tham số).
a) phương trình hoành độ giao điểm của (P) và (d) là:
x2 = 2x + m ⇔ x2 - 2x - m = 0
Δ'= 1 + m
(d) tiếp xúc với (P) khi phương trình hoành độ giao điểm có duy nhất 1 nghiệm
⇔ Δ'= 1 + m = 0 ⇔ m = -1
Khi đó hoành độ giao điểm là x = 1
b) (d) cắt (P) tại 2 điểm A, B phân biệt nằm về 2 phía của trục tung khi và chỉ khi
Khi đó 2 nghiệm của phương trình là:
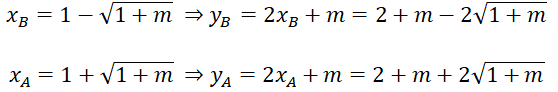
Kẻ BB' ⊥ OM ; AA' ⊥ OM
Ta có:
SAOM = 1/2 AA'.OM ; SBOM = 1/2 BB'.OM
Theo bài ra:
Do m > 0 nên m = 8
Vậy với m = 8 thì thỏa mãn điều kiện đề bài.
Bài 4
a) Xét tứ giác AEFB có:
∠(AFB) = 90o ( AF là đường cao)
∠(AEB) = 90o ( BE là đường cao)
⇒ 2 đỉnh E và F cùng nhìn cạnh AB dưới 1 góc bằng nhau
⇒ AEFB là tứ giác nội tiếp.
b) Xét ΔBEC và ΔAFC có:
∠(BCA) là góc chung
∠(BEC) = ∠(AFC) = 90 o
⇒ ΔBEC ∼ ΔAFC
c) Gọi P là trung điểm của AB
Do tam giác OAB cân tại O nên OP ⊥ AB
Tam giác OAP vuông tại P có:
⇒ Tứ giác CEIF là tứ giác nội tiếp và CI là đường kính đường tròn ngoại tiếp tứ giác CEIF
Ta có: IK ⊥ KC ( góc nội tiếp chắn nửa đường tròn ngoại tiếp tứ giác CEIF)
DK ⊥ KC (góc nội tiếp chắn nửa đường tròn (O)
⇒ D; I; K thẳng hàng (1)
Ta có:
DB ⊥ BC (góc nội tiếp chắn nửa đường tròn (O)
AI ⊥ BC ( AI là đường cao của tam giác ABC)
⇒ AI // BD
DA ⊥ BA(góc nội tiếp chắn nửa đường tròn (O)
BI ⊥ BA ( BI là đường cao của tam giác ABC)
⇒ AD // BI
Xét tứ giác ADBI có: AI // BD và AD // BI
⇒ ADBI là hình bình hành
Do P là trung điểm của AB ⇒ P là trung điểm của DI
Hay D; P; I thẳng hàng (2)
Từ (1) và (2) ⇒ D; P; K thẳng hàng.
...................................................................................
Đề thi Toán 9 Học kì 2 năm 2024 có đáp án (20 đề) - Đề 4
Phòng Giáo dục và Đào tạo .....
Đề thi Học kì 2
Môn: Toán lớp 9
Thời gian làm bài: 90 phút
(Đề 4)
Bài 1: (1,5 điểm) Giải phương trình và hệ phương trình
a) 2x2 - 3x + 1 = 0
b) x3 - 3x2 + 2 = 0
Bài 2: (1,5 điểm)
a) Vẽ đồ thị (P) hàm số y = x2
b) Tìm m để đường thẳng (d) : y = 2x + m tiếp xúc với (P).
Bài 3: (1,5 điểm) Cho phương trình (ấn số x): x2 – 4x + m – 2 = 0 (1)
a) Giá trị nào của m thì phương trình (1) có nghiệm
b) Tìm m để phương trình (1) có 2 nghiệm x1, x2 thỏa mãn 3x1 – x2 = 8
Bài 4: (1 điểm) Một ô tô đi từ A đến B với một vận tốc xác định. Nếu vận tốc tăng thêm 30 km/h thì thời gian đi sẽ giảm 1 giờ. Nếu vận tốc giảm bớt 15 km/h thì thời gian đi tăng thêm 1 giờ. Tính vận tốc và thời gian đi từ A đến B của ô tô.
Bài 5: (3,5 điểm) Cho tam giác nhọn ABC (AB < AC). Đường tròn tâm O đường kính BC cắt AB và AC lần lượt tại E và D. Gọi H là giao điểm của BD và CE; AH cắt BC tại I.
a) Chứng minh AI vuông góc với BC và EC là phân giác của góc IED.
b) Chứng minh BE.BA = BI.BC
c) Chứng minh tứ giác OIED nội tiếp.
d) Cho biết BC = 16cm. Tính BE.BA + CD.CA
Đáp án và Hướng dẫn giải
Bài 1:
a) 2x2 - 3x + 1 = 0
a = 2; b = - 3; c = 1 ⇒ a + b + c = 0
Do đó phương trình có nghiệm x1 = 1; x2 = 1/2
b) x3 - 3x2 + 2 = 0
⇔ x3 - x2 - 2x2 + 2 = 0
⇔ x2(x - 1) - 2(x2 - 1) = 0
⇔ x2(x - 1) - 2(x + 1)(x - 1) = 0
⇔ (x - 1)[x2 - 2(x + 1)] = 0
⇔ (x - 1)(x2 - 2x - 2) = 0
* Ta có: x - 1 = 0 khi x = 1
* Xét x2 – 2x - 2 = 0 (*)
Có ∆' = (-1)2 - 1(-2) = 3 > 0 nên phương trình (*) có 2 nghiệm phân biệt:
x1 = 1 + √3; x2 = 1 - √3
Vậy phương trình đã cho có tập nghiệm là S = {1 - √3; 1; 1 + √3}
Khi đó hệ phương trình trở thành:
Bài 2:
a) Tập xác định của hàm số: R
Bảng giá trị
| x | - 2 | - 1 | 0 | 1 | 2 |
| y = x2 | 4 | 1 | 0 | 1 | 2 |
Đồ thị hàm số y = x2 là đường parabol nằm phía trên trục hoành, nhận trục Oy làm trục đối xứng và điểm O(0;0) là đỉnh và là điểm thấp nhất.
b) Phương trình hoành độ giao điểm của (P) và (d) là x2 = 2x + m ⇔ x2 - 2x - m = 0
Δ' = 1-(-m) = 1 + m
(d) tiếp xúc với (P) khi và chỉ khi phương trình hoành độ giao điểm của (P) và d có một nghiệm duy nhất
⇔ Δ' = 0 ⇔ 1 + m = 0 ⇔ m = -1
Vậy với m = -1 thì d tiếp xúc với (P)
Bài 3:
a) Δ' = 22 - (m - 2) = 6 - m
Phương trình đã cho có nghiệm khi và chỉ khi Δ' ≥ 0
⇔ 6 - m ≥ 0 ⇔ m ≤ 6
Vậy với m ≤ 6 thì phương trình đã cho có nghiệm
b) Theo hệ thức Vi-et ta có:
Theo bài ra:
3x1 - x2 = 8
⇔ 3x1 - x2 = 2(x1 + x2)
⇔ x1 = 3x2
Khi đó: x1 + x2 = 4 ⇔ 3x2 + x2 = 4 ⇔ 4x2 = 4 ⇔ x2 = 1
⇒ x1 = 3
⇒ x1 x2 = 3 ⇒ m - 2 = 3 ⇔ m = 5
Vậy với m = 5 thì phương trình có 2 nghiệm thỏa mãn yêu cầu đề bài.
Bài 4:
Gọi vận tốc dự định của ô tô là x (km/h) (x > 15)
Thời gian dự định đi của ô tô là y (h) (y > 1)
⇒ Quãng đường AB là xy (km)
Nếu vận tốc tăng 30 km/h thì thời gian giảm đi 1h nên ta có phương trình:
(x + 30)(y - 1) = xy ⇔ -x + 30y = 30 (1)
Nếu vận tốc giảm 15 km/h thì thời gian tăng 1h nên ta có phương trình
(x - 15)(y + 1) = xy ⇔ x - 15y = 15 (2)
Từ (1) và (2) ta có hệ phương trình:
Vậy vận tốc đi từ A đến B là 60 km/h
Thời gian đi từ A đến B là 3h.
Bài 5:
a) Chứng minh AI BC
Ta có ∠BEC = BDC = 90o (hai góc nội tiếp chắn nửa đườn tròn)
d) Tính BE.BA + CD.CA
Chứng minh tương tự câu b, CD.CA = CI.CB
Từ đó BE.BA + CD.CA = BI.BC + CI.CB
= (BI + CI).BC = BC.BC = BC2 = 162 = 256
Đề thi Toán 9 Học kì 2 năm 2024 có đáp án (20 đề) - Đề 5
Phòng Giáo dục và Đào tạo .....
Đề thi Học kì 2
Môn: Toán lớp 9
Thời gian làm bài: 90 phút
(Đề 5)
Bài 1 (2,0 điểm):
a) Tính giá trị của biểu thức khi
b) Rút gọn biểu thức với
c) Tìm giá trị của thỏa mãn
Bài 2 (2,0 điểm): Giải bài toán bằng cách lập phương trình hoặc hệ phương trình:
Một xưởng theo kế hoạch phải in 6000 quyển sách giống nhau trong một thời gian quy định, với số quyển sách in được trong mỗi ngày là như nhau. Khi thực hiện mỗi ngày xưởng đã in nhiều hơn 300 quyển so với trong kế hoạch, nên xưởng đã in xong số quyển sách nói trên sớm hơn một ngày. Tính số quyển sách xưởng in được trong một ngày theo kế hoạch.
Bài 3 (2,0 điểm):
Cho phương trình:
a) Giải phương trình khi
b) Tìm để phương trình có hai nghiệm phân biệt thỏa mãn
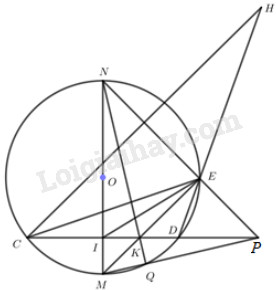
Bài 4 (3,5 điểm):
Cho đường tròn đường kính Kẻ tiếp tuyến và lấy trên tiếp tuyến đó một điểm sao cho từ kẻ tiếp tuyến tiếp xúc với tại .
a) Chứng minh tứ giác nội tiếp một đường tròn.
b) Chứng minh
c) Đường thẳng vuông góc với ở cắt tia tại Chứng minh tứ giác là hình bình hành.
d) Biết cắt tại cắt tại và kéo dài cắt nhau tại Chứng minh ba điểm thẳng hàng.
Bài 5 (0,5 điểm):
Cho hai số dương thỏa mãn
Tìm giá trị nhỏ nhất của biểu thức
Phương pháp giải:
a) Tìm điều kiện xác định, thay giá trị của vào biểu thức và tính giá trị của biểu thức.
b) Quy đồng mẫu các phân thức, biến đổi và rút gọn biểu thức đã cho.
c) Thay biểu thức vừa rút gọn ở câu trên vào bất phương trình, giải bất phương trình tìm
Đối chiếu với điều kiện rồi kết luận.
Đáp án và Hướng dẫn giải
a) Tính giá trị của biểu thức khi
Điều kiện xác định:
Thay vào biểu thức ta có:
Vậy thì
b) Rút gọn biểu thức với
Với ta có:
Vậy với
c) Tìm giá trị của thỏa mãn
Điều kiện:
Kết hợp điều kiện, ta được thỏa mãn yêu cầu đề bài.
Vậy thỏa mãn điều kiện bài toán.
Bài 2:
Phương pháp giải:
Gọi số sách xưởng dự định in trong một ngày theo kế hoạch là (quyển),
Biểu diễn các đại lượng chưa biết theo ẩn vừa gọi và các đại lượng đã biết.
Lập phương trình, giải phương trình tìm
Đối chiếu với điều kiện rồi kết luận.
Lời giải chi tiết:
Gọi số sách xưởng dự định in trong một ngày theo kế hoạch là (quyển),
Số ngày hoàn thành theo dự định là: (ngày).
Số sách thực tế mà xưởng in được trong một ngày là: (quyển).
Số ngày hoàn thành thực tế là: (ngày).
Vì thực tế, xưởng in xong sớm hơn một ngày, nên ta có phương trình:
Vậy số sách xưởng dự định in trong một ngày theo kế hoạch là 1200 quyển.
Bài 3:
Phương pháp giải:
a) Thay vào phương trình, giải phương trình bậc hai một ẩn.
b) Tìm điều kiện của để phương trình đã cho có hai nghiệm phân biệt
Áp dụng định lý Vi-et và biểu thức đã cho để tìm
Đối chiếu với điều kiện rồi kết luận.
Lời giải chi tiết:
Cho phương trình: (*)
a) Giải phương trình khi
Thay vào phương trình (*) đã cho, ta được phương trình:
Vậy khi thì phương trình có nghiệm
b) Tìm để phương trình có hai nghiệm phân biệt thỏa mãn
Ta có:
Phương trình đã cho có hai nghiệm phân biệt
Theo hệ thức Vi-ét ta có:
Vì là nghiệm của phương trình (*) nên ta có:
Theo đề bài ta có:
Vậy .
Bài 4:
Phương pháp giải:
a) Chứng minh tứ giác nội tiếp dựa vào các dấu hiệu nhận biết.
b) Chứng minh hai đường thẳng cùng vuông góc với
c) Chứng minh
d) Chứng minh là trực tâm của và là một đường cao của
Lời giải chi tiết:
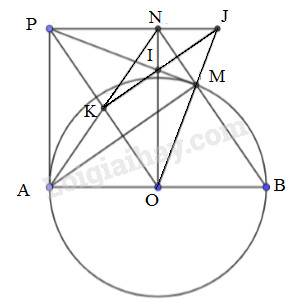
a) Chứng minh tứ giác nội tiếp một đường tròn.
Ta có: là tiếp tuyến của
Lại có: cũng là tiếp tuyến của
Xét tứ giác ta có: mà hai góc ở vị trí đối nhau
là tứ giác nội tiếp. (dhnb)
b) Chứng minh
Xét đường tròn có là hai tiếp tuyến cắt nhau tại (tính chất)
thuộc đường trung trực của (1)
Lại có: thuộc đường trung trực của (2)
Từ (1) và (2) ta có là đường trung trực của
Lại có: là góc nội tiếp chắn nửa đường tròn hay
(cùng ).
c) Đường thẳng vuông góc với ở cắt tia tại Chứng minh tứ giác là hình bình hành.
Ta có: (hai góc đồng vị).
Xét và ta có:
(cạnh huyền- góc nhọn)
(hai cạnh tương ứng bằng nhau).
Xét tứ giác ta có:
là hình bình hành. (dhnb)
d) Biết cắt tại cắt tại và kéo dài cắt nhau tại Chứng minh ba điểm thẳng hàng.
Ta có: (hai cạnh tương ứng).
Lại có:
là hình bình hành. (dhnb)
Mà là hình chữ nhật. (dhnb)
Mặt khác: là trung điểm của của (tính chất hình bình hành)
Xét ta có: và là hai tiếp tuyến cắt nhau tại
là tia phân giác của
Hay
Mà (hai góc so le trong)
cân tại
Mà là trung điểm của nên vừa là đường trung tuyến trong tam giác cân .
Suy ra cũng là đường cao của (*)
Ta có: ( là tiếp tuyến của )
là đường cao của
Lại có: ( là hình chữ nhật)
là đường cao của
Mà là trực tâm (**)
Từ (*) và (**) thẳng hàng.
Bài 5:
Phương pháp giải:
Chọn điểm rơi và sử dụng hệ quả của bất đẳng thức AM-GM.
Lời giải chi tiết:
Cho hai số dương thỏa mãn
Tìm giá trị nhỏ nhất của biểu thức
Trước tiên, theo bất đẳng thức AM-GM:
Với nhân theo vế hai bất đẳng thức này ta được:
Ta có:
Sử dụng hệ quả (*) ta có: (do )
Lại có :
Vì
Suy ra
Dấu “=” xảy ra
Vậy giá trị nhỏ nhất của là khi
Đề thi Toán 9 Học kì 2 năm 2024 có đáp án (20 đề) - Đề 6
Phòng Giáo dục và Đào tạo .....
Đề thi Học kì 2
Môn: Toán lớp 9
Thời gian làm bài: 90 phút
(Đề 6)
Câu 1 (1,5 điểm): Giải các phương trình sau:
a)
b)
Câu 2 (1,5 điểm): Cho hàm số: có đồ thị là (P).
a) Vẽ (P).
b) Tìm các tọa độ giao điểm của (P) và đường thẳng (D): bằng phép toán.
Câu 3 (1,5 điểm): Một khu vườn hình chữ nhật có chu vi 70m. Tính diện tích khu vườn biết 2 lần chiều dài nhỏ hơn 3 lần chiều rộng 5m.
Câu 4 (1 điểm): Một xí nghiệp may cần thanh lý 1410 bộ quần áo. Biết mỗi ngày xí nghiệp đó bán được 30 bộ quần áo. Gọi x là số ngày đã bán, y là số bộ quần áo còn lại sau x ngày bán.
a) Hãy lập công thức tính y theo x.
b) Xí nghiệp cần bao nhiêu ngày để bán hết số bộ quần áo cần thanh lý?
Câu 5 (1 điểm):
Cho A là điểm thuộc nửa đường tròn (O) đường kính và . Tính AB, AC và diện tích phần tô đậm.
Câu 6 (1,5 điểm):
Cho phương trình: (x là ẩn).
a) Tìm m để phương trình có hai nghiệm và .
b) Gọi và là hai nghiệm của phương trình trên. Tìm m để .
Câu 7 (2 điểm):
Cho nhọn () nội tiếp đường tròn , các đường cao BE và CF cắt nhau tại H.
a) Chứng minh tứ giác AEHF và BCEF nội tiếp.
b) Hai đường thẳng EF và BC cắt nhau tại I. Vẽ tiếp tuyến ID với (D là tiếp điểm, D thuộc cung nhỏ BC). Chứng minh .
c) DE, DF cắt đường tròn tại M và N. Chứng minh NM // EF.
Đáp án và Hướng dẫn giải
Bài 1:
Phương pháp giải:
a) Sử dụng công thức nghiệm của phương trình bậc 2 để giải
b) Đặt để đưa phương trình đề bài thành phương trình bậc 2 sau đó dùng công thức nghiệm giải tìm t sau đó tìm x.
Lời giải chi tiết:
a)
Vậy phương trình có hai nghiệm phân biệt và
b)
Đặt khi đó phương trình trở thành: (1)
Giải phương trình (1), ta có:
Gọi là hai nghiệm phân biệt của (1)
Với ta có:
Vậy phương trình có hai nghiệm và
Bài 2:
Phương pháp giải:
a) Lập bảng giá trị và vẽ đồ thị.
b) Lập phương trình hoành độ giao điểm, giải phương trình bậc 2 để tìm.
Lời giải chi tiết:
Cho hàm số: có đồ thị là (P).
a) Vẽ (P).
Bảng giá trị:
|
x |
|
|
0 |
1 |
2 |
|
|
|
|
0 |
|
|
Vậy đồ thị hàm số là đường cong đi qua các điểm
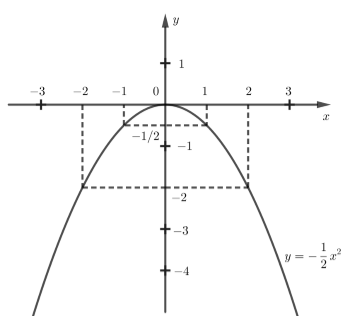
b) Tìm các tọa độ giao điểm của (P) và đường thẳng (D): bằng phép toán.
Phương trình hoành độ giao điểm của (P) và (D) là:
Ta có: hoặc
Với
Với
Vậy các giao điểm của (P) và (D) là 2 điểm và
Bài 3:
Phương pháp giải:
Phân tích đề bài, giải bài toán bằng cách lập hệ phương trình để tìm chiều dài chiều rộng khu vườn, sau đó tính diện tích.
Diện tích hình chữ nhật bằng tích của chiều dài với chiều rộng.
Lời giải chi tiết:
Gọi chiều dài và chiều rộng của khu vườn lần lượt là và
Vì khu vườn hình chữ nhật có chu vi 70m nên ta có:
Lại có 2 lần chiều dài nhỏ hơn 3 lần chiều rộng 5m nên ta có phương trình:
Từ (1) và (2) ta có hệ phương trình:
Vì khu vườn hình chữ nhật nên diện tích khu vườn là:
Vậy diện tích khu vườn là
Bài 4:
Phương pháp giải:
a) Tính số quần áo bán được sau x ngày bán từ đó suy ra y theo x.
b) Bán hết thì thế vào công thức ở a) để tính số ngày x.
Lời giải chi tiết:
a) Mỗi ngày xí nghiệp đó bán được 30 bộ quần áo nên sau x ngày bán xí nghiệp đó bán được 30x bộ quần áo.
y là số bộ quần áo còn lại sau x ngày bán (1)
b) Để xí nghiệp bán hết số bộ quần áo cần thanh lý thì
Thay vào (1) ta được:
(ngày)
Vậy xí nghiệp cần 47 ngày để bán hết số bộ quần áo cần thanh lý.
Bài 5:
Phương pháp giải:
Chứng minh tam giác ABC vuông tại A từ đó sử dụng mối quan hệ giữa cạnh và góc trong tam giác vuông để tính AB, AC.
Để tính diện tích phần tô đậm ta lấy diện tích nửa hình tròn (O) đường kính BC trừ đi diện tích tam giác ABC.
Lời giải chi tiết:
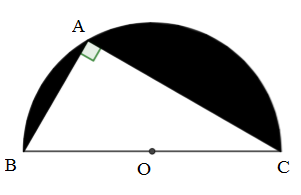
Ta có A là điểm thuộc nửa đường tròn (O) đường kính
(góc nội tiếp chắn nửa đường tròn)
Xét tam giác ABC vuông tại A ta có:
Gọi diện tích nửa hình tròn (O) đường kính là P
Gọi diện tích tam giác ABC là S
Gọi diện tích phần tô đậm là Q
Bài 6:
Phương pháp giải:
a) Sử dụng công thức nghiệm thu gọn, để phương trình có 2 nghiệm thì
b) Kết hợp câu a), biến đổi biểu thức đề bài sao cho chỉ còn và , sử dụng hệ thức Vi-ét thế vào để tìm m.
Lời giải chi tiết:
a) Tìm m để phương trình có hai nghiệm và .
Xét phương trình:
Có
Phương trình có hai nghiệm và
Vậy với thì phương trình có hai nghiệm và .
b) Gọi và là hai nghiệm của phương trình trên. Tìm m để .
Theo a) để phương trình có hai nghiệm và thì
Theo hệ thức Vi-ét ta có:
Ta có:
Vậy với thỏa mãn yêu cầu đề bài.
Bài 7:
Phương pháp giải:
a) Chứng minh A, E, H, F cùng thuộc một đường tròn để suy ra là tứ giác nội tiếp, chứng minh tứ giác BCEF có hai đỉnh kề nhau cùng nhìn cạnh chứa hai đỉnh còn lại dưới cùng một góc .
b) Chứng minh để suy ra đpcm
c) Chứng minh hai góc ở vị trí đồng vị bằng nhau dựa vào các định lý Talet thuận và đảo để suy ra các tam giác đồng dạng.
Lời giải chi tiết:
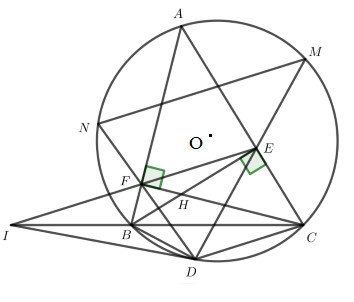
a) Chứng minh tứ giác AEHF và BCEF nội tiếp.
Xét tứ giác có E, F thuộc đường tròn đường kính AH
A, E, H, F cùng thuộc một đường tròn đường kính
là tứ giác nội tiếp (dhnb).
Xét tứ giác có hay hai đỉnh kề nhau cùng nhìn cạnh dưới các góc vuông nên BCEF là tứ giác nội tiếp (dhnb)
b) Hai đường thẳng EF và BC cắt nhau tại I. Vẽ tiếp tuyến ID với (D là tiếp điểm, D thuộc cung nhỏ BC). Chứng minh .
Xét đường tròn có (góc tạo bởi tiếp tuyến và dây cung và góc nội tiếp cùng chắn cung )
Xét và có:
chung
(chứng minh trên)
c) DE, DF cắt đường tròn tại M và N. Chứng minh NM // EF.
Vì BCEF là tứ giác nội tiếp (theo câu a) nên xét đường tròn ngoại tiếp tứ giác có (hai góc nội tiếp cùng chắn cung )
Xét và có:
chung
(chứng minh trên)
Theo câu b) ta có
Xét và có:
chung
(2 góc tương ứng)
Mặt khác, xét đường tròn có ID là tiếp tuyến nên (góc tạo bởi tia tiếp tuyến và dây cung và góc nội tiếp cùng chắn cung )
Mà hai góc này ở vị trí đồng vị
Đề thi Toán 9 Học kì 2 năm 2024 có đáp án (20 đề) - Đề 7
Phòng Giáo dục và Đào tạo .....
Đề thi Học kì 2
Môn: Toán lớp 9
Thời gian làm bài: 90 phút
(Đề 7)
Bài 1 (2,0 điểm):
Cho biểu thức với
1. Rút gọn
2. Tìm các giá trị của để
Bài 2 (2,0 điểm):
1. Giải hệ phương trình:
2. Trong vườn trường người ta xây một bồn hoa gồm hai hình tròn tâm và tâm tiếp xúc ngoài với nhau, có . Tính bán kính của mỗi hình tròn biết diện tích bồn hoa bằng và bán kính hình tròn tâm lớn hơn bán kính đường tròn tâm
Bài 3 (2,5 điểm):
Cho parabol và đường thẳng (với là tham số).
1. Tìm tọa độ các giao điểm của và khi
2. Tìm để cắt tại hai điểm nằm về hai phía của trục tung.
3. Tìm để cắt tại hai điểm phân biệt có tung độ là thỏa mãn
Bài 4 (3 điểm):
Cho đường tròn và dây cung cố định, là điểm di động trên cung sao cho tam giác nhọn. Hai đường phân giác trong của góc và cắt nhau ở và thứ tự cắt đường tròn ở . Đường thẳng cắt ở .
1. Chứng minh tứ giác nội tiếp. Hãy chỉ ra một tứ giác nội tiếp tương tự.
2. Chứng minh tứ giác là hình thoi.
3. Chứng minh tam giác cân. Tìm vị trí của để có độ dài lớn nhất.
Bài 5 (0,5 điểm):
Cho là các số thực dương thỏa mãn: Tìm giá trị nhỏ nhất của biểu thức:
Đáp án và Hướng dẫn giải
Bài 1:
Phương pháp giải:
1. Quy đồng mẫu số rồi rút gọn biểu thức.
2. Giải bất phương trình để tìm đối chiếu với điều kiện rồi kết luận.
Lời giải chi tiết:
Cho biểu thức với
1. Rút gọn
Điều kiện xác định:
Vậy với .
2. Tìm các giá trị của để
Điều kiện xác định:
( với mọi )
Kết hợp với ĐKXĐ ta có: thì
Bài 2:
Phương pháp giải:
1. Đặt điều kiện, biến đổi hệ phương trình say đó giải hệ phương trình bằng phương pháp cộng đại số.
2. Gọi bán kính hình tròn tâm và tâm lần lượt là
Biểu diễn các dữ kiện đã biết theo hai ẩn đã gọi.
Lập hệ phương trình, giải hệ phương trình.
So sánh với điều kiện rồi kết luận.
Lời giải chi tiết:
1. Giải hệ phương trình:
Điều kiện xác định:
Vậy hệ phương trình có nghiệm
2. Trong vườn trường người ta xây một bồn hoa gồm hai hình tròn tâm A và tâm B tiếp xúc ngoài với nhau, có AB=3m. Tính bán kính của mỗi hình tròn biết diện tích bồn hoa bằng và bán kính hình tròn tâm A lớn hơn bán kính đường tròn tâm B
Gọi bán kính hình tròn tâm và tâm lần lượt là
Vì 2 đường tròn tiếp xúc ngoài với nhau nên:
Diện tích của hai vườn hoa hình tròn tâm và tâm lần lượt là: và
Lại có diện tích bồn hoa bằng tổng diện tích của hai hình tròn bằng nên:
Từ (1) và (2) ta có hệ phương trình:
Vậy bán kính của hai khu vường hình tròn tâm và tâm lần lượt là: và
Bài 3:
Phương pháp giải:
1. Thay để tìm phương trình đường thẳng , giải phương trình hoành độ giao điểm để tìm giao điểm của và để tìm hoành độ các giao điểm.
Thay hoành độ giao điểm vừa tìm được vào công thức hàm số của hoặc để tìm tung độ các giao điểm.
2. Hai điểm nằm về hai phía trục tung khi có các giao điểm có hoành độ trái dấu.
Khi đó phương trình hoành độ giao điểm có hai nghiệm trái dấu
3. Xét phương trình hoành độ giao điểm của và
cắt tại hai điểm phân biệt có hai nghiệm phân biệt
Biểu diễn theo rồi sử dụng hệ thức Vi-et để có phương trình ẩn . Giải phương trình ta tìm được
Lời giải chi tiết:
Cho parabol và đường thẳng (với là tham số).
1. Tìm tọa độ các giao điểm của và khi
Khi ta có:
Xét phương trình hoành độ giao điểm của và ta có:
Vậy khi thì giao điểm của và là hai điểm .
2. Tìm để cắt tại hai điểm nằm về hai phía của trục tung.
Xét phương trình hoành độ giao điểm của và ta có:
cắt tại hai điểm phân biệt nằm về hai phía của trục tung có hai nghiệm trái dấu
Vậy thỏa mãn bài toán.
3. Tìm để cắt tại hai điểm phân biệt có tung độ là thỏa mãn
Xét phương trình hoành độ giao điểm của và ta có:
Đường thẳng cắt tại hai điểm phân biệt có hai nghiệm phân biệt
Vậy với thì đường thẳng cắt tại hai điểm phân biệt
Áp dụng định lý Vi-ét ta có:
Theo đề bài ta có:
Vậy thỏa mãn bài toán.
Bài 4:
Phương pháp giải:
1. Sử dụng các dấu hiệu nhận biết của tứ giác nội tiếp.
2. Sử dụng các dấu hiệu nhận biết hình thoi.
Lời giải chi tiết:
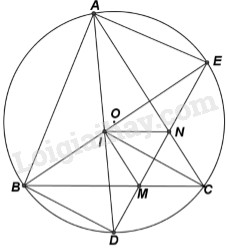
1. Chứng minh tứ giác nội tiếp. Hãy chỉ ra một tứ giác nội tiếp tương tự.
Ta có là phân giác của góc và nên:
(tính chất góc nội tiếp bằng nhau thì chắn các cung bằng nhau).
Lại có: là góc nội tiếp chắn cung
Và là góc nội tiếp chắn cung
(hai góc nội tiếp chắn hai cung bằng nhau thì bằng nhau).
Hay
Xét tứ giác ta có:
Mà hai góc này là hai góc có đỉnh cùng kề cạnh
là tứ giác nội tiếp (dhnb).
Chứng minh tương tự ta có tứ cũng là tứ giác nội tiếp.
2. Chứng minh tứ giác là hình thoi.
Do tứ giác nội tiếp (cmt) (hai góc nội tiếp cùng chắn cung )
Lại có: (hai góc nội tiếp cùng chắn cung của đường tròn )
Mà hai góc này là hai góc đồng vị
Tương tự ta chứng minh được
Xét tứ giác có:
là hình bình hành (dhnb).
Lại có hai đường phân giác trong của góc và cắt nhau ở (gt)
là đường phân giác của của
là phân giác của góc
Hình bình hành có đường chéo là đường phân giác của
là hình thoi. (đpcm)
3. Chứng minh tam giác cân. Tìm vị trí của để có độ dài lớn nhất.
Ta có tứ giác là tứ giác nội tiếp (cmt)
(hai góc nội tiếp cùng chắn cung )
Xét đường tròn ta có:
là góc có đỉnh nằm trong đường tròn chắn cung và cung
Mà là góc nội tiếp chắn cung
cân tại (đpcm).
Bài 5:
Phương pháp giải:
Áp dụng bất đẳng thức Cô-si cho 2 số không âm:
Dấu “=” xảy ra khi
Lời giải chi tiết:
Có
Và tương tự ta có:
GTNN của là .
Đề thi Toán 9 Học kì 2 năm 2024 có đáp án (20 đề) - Đề 8
Phòng Giáo dục và Đào tạo .....
Đề thi Học kì 2
Môn: Toán lớp 9
Thời gian làm bài: 90 phút
(Đề 8)
Câu 1 (2,0 điểm):
Cho hai biểu thức: với
1) Rút gọn biểu thức A.
2) Tìm x biết .
3) Tìm giá trị nhỏ nhất của biểu thức .
Câu 2 (2,0 điểm): Giải bài toán sau bằng cách lập phương trình hoặc hệ phương trình.
Một ô tô đi từ A đến B cách nhau 90 km với vận tốc dự định. Khi từ B trở về A, ô tô đi với vận tốc nhanh hơn vận tốc lúc đi là 5 km/giờ. Do đó thời gian về ít hơn thời gian đi là 15 phút. Tính vận tốc dự định của ô tô khi đi từ A đến B.
Câu 3 (2,0 điểm):
1) Giải hệ phương trình:
2) Trong mặt phẳng tọa độ Oxy cho đường thẳng (m là tham số) và parabol
a) Với , tìm tọa độ giao điểm của đường thẳng và parabol .
b) Tìm m để đường thẳng cắt parabol tại hai điểm phân biệt có hoành độ thỏa mãn .
Câu 4 (3,5 điểm):
1. Một hộp sữa hình trụ có đường kính đáy là 12 cm, chiều cao là 10 cm. Tính diện tích vật liệu dùng để tạo nên một vỏ hộp như vậy (không tính phần mép nối).
2. Cho đường tròn , từ điểm A nằm ngoài đường tròn vẽ hai tiếp tuyến AB, AC với đường tròn (B, C lần lượt là các tiếp điểm).
a) Chứng minh tứ giác ABOC nội tiếp.
b) Gọi D là trung điểm của AC, BD cắt đường tròn tại E, đường thẳng AE cắt đường tròn tại điểm thứ hai F. Chứng minh .
c) Chứng minh
Câu 5 (0,5 điểm):
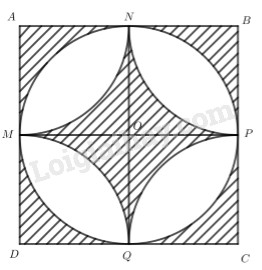
Một viên gạch hình vuông cạnh a (cm) có hoa văn như hình vẽ. M, N, P, Q lần lượt là trung điểm các cạnh AD, AB, BC, CD. Tìm độ dài a biết diện tích phần gạch chéo là (cm2)
Đáp án và Hướng dẫn giải
Bài 1:
Phương pháp giải:
+ Quy đồng và rút gọn phân thức
+ Tính và đưa P về dạng một tổng bình phương cộng một số.
Lời giải chi tiết:
Cho hai biểu thức: với
1) Rút gọn biểu thức A.
Điều kiện:
2) Tìm x biết .
Điều kiện:
Vậy không có giá trị nào của x để .
3) Tìm giá trị nhỏ nhất của biểu thức .
Điều kiện:
Ta có , dấu “=” xảy ra
Vậy giá trị nhỏ nhất của P là khi .
Bài 2:
Phương pháp giải:
+ Phân tích kỹ đề bài, gọi vận tốc dự định của ô tô khi đi từ A đến B là
+ Dựa vào dữ kiện đề bài để lập phương trình giải tìm x.
Lời giải chi tiết:
Gọi vận tốc dự định của ô tô khi đi từ A đến B là
Khi đó thờ gian ô tô đi từ A đến B là
Vận tốc ô tô khi đi từ B trở về A là
Thời gian ô tô đi từ B trở về A là
15 phút giờ
Vì thời gian về ít hơn thời gian đi là 15 phút nên ta có phương trình:
Vậy vận tốc dự định của ô tô là
Bài 3:
Phương pháp giải:
1) Giải hệ phương trình bằng cách đặt ẩn phụ.
2) a) Thay vào , giải phương trình hoành độ giao điểm để tìm giao điểm của chúng.
b) Phương trình có hai nghiệm phân biệt . Sử dụng định lý Vi-ét biến đổi phương trình đã cho theo m để giải tìm m
Lời giải chi tiết:
1) Giải hệ phương trình:
Điều kiện :
Đặt Khi đó hệ phương trình trở thành:
Vậy nghiệm của hệ phương trình là
2) Trong mặt phẳng tọa độ Oxy cho đường thẳng (m là tham số) và parabol
a) Với , tìm tọa độ giao điểm của đường thẳng và parabol .
Với ta có phương trình đường thẳng
Xét phương trình hoành độ giao điểm của và là:
+) Với
+) Với
Vậy với thì đường thẳng cắt parabol tại hai điểm phân biệt có tọa độ và
b) Tìm m để đường thẳng cắt parabol tại hai điểm phân biệt có hoành độ thỏa mãn .
Xét phương trình hoành độ giao điểm của và là:
(1)
Ta có mới mọi m
Do đó phương trình (1) luôn có 2 nghiệm phân biệt
Đường thẳng cắt parabol tại hai điểm phân biệt có hoành độ
Theo định lý Vi-ét ta có:
Theo đề bài
Vậy với hoặc thỏa mãn yêu cầu đề bài.
Bài 4:
Phương pháp giải:
1) Diện tích đường tròn đáy của hình trụ có bán kính là
Diện tích xung quanh của hình trụ có bán kính đáy và chiều cao là
Diện tích toàn phần của hình trụ là
2) a) Chứng minh ABOC là tứ giác có tổng hai góc đối bằng
b) Chứng minh để suy ra đpcm
c) Chứng minh cân tại C
Lời giải chi tiết:
1. Một hộp sữa hình trụ có đường kính đáy là 12 cm, chiều cao là 10 cm. Tính diện tích vật liệu dùng để tạo nên một vỏ hộp như vậy (không tính phần mép nối).
Ta có bán kính đáy là: 6 (cm)
Diện tích một đáy của hình trụ là:
Diện tích xung quanh là:
Diện tích vật liệu tạo nên vỏ hộp sữa là:
2. Cho đường tròn , từ điểm A nằm ngoài đường tròn vé hai tiếp tuyến AB, AC với đường tròn (B, C lần lượt là các tiếp điểm).
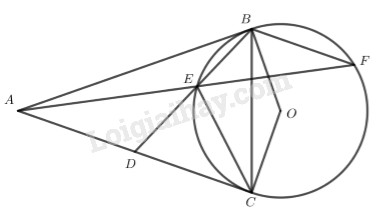
a) Chứng minh tứ giác ABOC nội tiếp.
Vì AB, AC là hai tiếp tuyến của đường tròn
(tính chất tiếp tuyến)
Xét tứ giác ABOC có
Mà hai góc này ở vị trí đối nhau Tứ giác ABOC nội tiếp (dhnb).
b) Gọi D là trung điểm của AC, BD cắt đường tròn tại E, đường thẳng AE cắt đường tròn tại điểm thứ hai F. Chứng minh .
Xét đường tròn có:
(góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cung cùng chắn cung BE)
Xét và có:
(đpcm)
c) Chứng minh .
Xét đường tròn có:
(góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cung cùng chắn cung EC)
Xét và có:
(cặp cạnh tương ứng tỉ lệ)
Mà
Xét và có:
(cặp góc tương ứng bằng nhau)
Mà
Lại có hai góc này ở vị trí so le trong
(2 góc so le trong)
Mà (góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cung cùng chắn một cung)
cân tại C (đpcm)
Bài 5:
Phương pháp giải:
Nhận thấy rằng phần gạch trắng tạo bởi 8 hình viên phân bằng nhau.
Diện tích hình viên phân bằng diện tích hình quạt trừ diện tích tam giác
Dựa vào đề bài, lập phương trình, giải tìm a
Lời giải chi tiết:
Nhận thấy rằng phần gạch trắng tạo bởi 8 hình viên phân bằng nhau.
Gọi là bán kính hình tròn. Diện tích một hình viên phân là:
Vậy diện tích hình gồm 8 viên phân bằng
Diện tích phần gạch chéo bằng:
Vì diện tích phần gạch chéo là nên ta có:
Vậy
Đề thi Toán 9 Học kì 2 năm 2024 có đáp án (20 đề) - Đề 9
Phòng Giáo dục và Đào tạo .....
Đề thi Học kì 2
Môn: Toán lớp 9
Thời gian làm bài: 90 phút
(Đề 9)
Câu 1: Giải các phương trình và hệ phương trình:
Câu 2: Cho hàm số:
a) Vẽ đồ thị (P) và (d) trên cùng trục tọa độ Oxy.
b) Tìm tọa độ giao điểm d và P bằng phép toán.
Câu 3: Cho phương trình:
a) Chứng minh rằng phương trình luôn có 2 nghiệm phân biệt với mọi giá trị của
b) Tìm m để phương trình có 2 nghiệm phân biệt thỏa mãn hệ thức:
Câu 4: Cần pha bao nhiêu lít nước ở và 8 lít nước ở để thu được lượng nước ?
Câu 5: Bạn Nam đi học từ nhà đến trường bằng xe đạp có bán kính bánh xe 700mm. Tính quãng đường từ nhà tới trường, biết bánh xe quay tất cả 875 vòng (giả sử bạn Nam đạp xe chạy thẳng từ nhà đến trường trên một đường thẳng và kết quả làm tròn đến chữ số thập phân thứ nhất).
Câu 6: Từ điểm S nằm ngoài (O; R), vẽ hai tiếp tuyến SA, SB (O) (B, C là hai tiếp điểm) và cát tuyến SCD (C nằm giữa S và D, tia SD nằm trong góc ASO).
a) Chứng minh: SAOB là tứ giác nội tiếp và:
b) Gọi H là giao điểm AB và OS. Chứng minh rằng:
c) Gọi I là trung điểm của CD. Chứng minh:
Đáp án và Hướng dẫn giải
Bài 1:
Phương pháp giải:
+) Đây là các phương trình bậc 2, ta đưa về phương trình tích để giải.
+) Đối với hệ phương trình bậc nhất 2 ẩn, ta sử dụng phép thế hoặc nhân hệ số rồi trừ 2 vế.
Lời giải chi tiết:
Vậy phương trình có tập nghiệm là:
Vậy phương trình có tập nghiệm là:
Vậy hệ phương trình có nghiệm là:
Bài 2:
Phương pháp giải:
1) Lập bảng giá trị các điểm thuộc đồ thị hàm số (P) và vẽ đồ thị hàm số.
2) Lập phương trình hoành độ giao điểm của (d) cắt (P).
+) Để (d) cắt (P) tại hai điểm phân biệt thì phương trình hoành độ giao điểm phải có hai nghiệm phân biệt tức là
Lời giải chi tiết:
Cho hàm số:
a) Vẽ đồ thị (P) và (d) trên cùng trục tọa độ Oxy.
Ta có bảng giá trị:
|
|
|
|
0 |
2 |
4 |
|
|
|
|
0 |
|
|
Vậy đồ thị hàm số là đường cong đi qua các điểm
|
|
0 |
|
|
|
|
|
Vậy đồ thị hàm số là đường thẳng đi qua các điểm
b) Tìm tọa độ giao điểm d và P.
Phương trình hoành độ giao điểm của và là:
Vậy tọa độ giao điểm (d) và (P) là:
Bài 3:
Phương pháp giải:
Bước 1: Tìm m để phương trình (1) có hai nghiệm phân biệt : Phương trình (1) có hai nghiệm phân biệt khi và chỉ khi
Bước 2: Phân tích biểu thức A về dạng chứa các hệ thức Viet sau đó áp dụng Viet vào tìm được m và đối chiếu với điều kiện sau đó kết luận. Hệ thức Viet như sau:
Lời giải chi tiết:
Cho phương trình:
a) Chứng minh rằng phương trình luôn có 2 nghiệm phân biệt.
Ta có:
với mọi
Do đó phương trình trên luôn có 2 nghiệm phân biệt với mọi
b) Tìm m để phương trình có 2 nghiệm phân biệt:
Áp dụng định lý Viet ta có:
Theo đề bài ta có :
Vậy giá trị cần tìm của m là :
Bài 4:
Phương pháp giải:
Sử dụng công thức phương trình cân bằng nhiệt:
Lời giải chi tiết:
Gọi lượng nước cần pha thêm là
Ta có: 3 lít = 3 kg.
Theo đề bài ta có :
Vậy cần pha thêm tổng cộng 4 lít nước.
Bài 5:
Phương pháp giải:
Giải bài toán bằng cách lập phương trình:
+) Gọi ẩn và đặt điều kiện cho ẩn.
+) Biểu diễn các đại lượng chưa biết theo ẩn vừa gọi và các đại lượng đã biết.
+) Dựa vào dữ kiện bài toán để lập phương trình.
+) Giải phương trình vừa lập sau đó đối chiếu với điều kiện đề bài và kết luận.
Lời giải chi tiết:
Gọi quãng đường từ nhà bạn Nam đến trường là
1 vòng bánh xe quay được 1 chu vi bánh xe là:
Vậy chiều dài từ nhà đến trường là: 3,8 km.
Bài 6:
Phương pháp giải:
a) Chứng minh đây là tứ giác có 2 góc đối vuông, từ đó sử dụng tam giác đồng dạng suy ra hệ thức.
b) Chứng minh OICH là tứ giác nội tiếp, tam giác OCD cân.
c) Gọi P là giao điểm SI và AP, chứng minh rằng
Lời giải chi tiết:
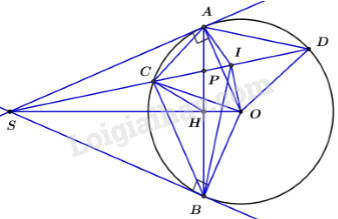
a) Chứng minh: SAOB là tứ giác nội tiếp và:
Ta có là hai tiếp tuyến của tại
là tứ giác nội tiếp (dhnb).
Ta có: (góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cung cùng chắn cung AC)
Xét và ta có:
b) Gọi H là giao điểm AB và OS. Chứng minh rằng:
Ta có: cân tại (hai góc kề đáy).
Có (tính chất 2 tiếp tuyến cắt nhau) và là đường trung trực của
Áp dụng hệ thức lượng trong có đường cao là có:
Xét và ta có:
(hai góc tương ứng).
c) Gọi I là trung điểm của CD. Chứng minh:
Gọi
Ta có là trung điểm của (liên hệ giữa đường kính và dây cung)
là tứ giác nội tiếp (dhnb).
Xét và ta có:
Xét và ta có:
(các góc tương ứng).
Ta có:
sđ cung BD
Xét và ta có:
(đpcm)
Đề thi Toán 9 Học kì 2 năm 2024 có đáp án (20 đề) - Đề 10
Phòng Giáo dục và Đào tạo .....
Đề thi Học kì 2
Môn: Toán lớp 9
Thời gian làm bài: 90 phút
(Đề 10)
PHẦN I: TRẮC NGHIỆM (3,0 điểm).
Chọn phương án trả lời đúng trong các câu sau:
Câu 1. Điều kiện để biểu thức M=1√x−1 xác định là
A. x>1
B. x>0
C. x>0;x≠1
D. x≥0;x≠1
Câu 2. Giá trị của biểu thức P=√3+2√2−√3−2√2 là
A. 2√2
B. −2
C. 2
D. −2√2
Câu 3. Cho tam giác ABC vuông tại A,∠ABC=600, cạnh AB=5cm. Độ dài cạnh AC là
A. 10cm
B. 5√32cm
C. 5√3cm
D. 5√3cm
Câu 4. Hình vuông cạnh bằng 2cm, bán kính đường tròn ngoại tiếp hình vuông là
A. 1cm B. 2cm
C. 2√2cm D.√2cm
Câu 5. Trong hình vẽ dưới đây, biết góc ∠ASC=400,SA là tiếp tuyến của đường tròn tâm O. Góc ∠ACS có số đo bằng
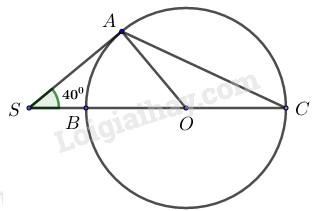
A. 400 B. 300
C. 250 D. 200
Câu 6. Số giá trị nguyên của m để hàm số y=(m2−9)x+3 nghịch biến là
A. 5 B. 4
C. 2 D. 3
PHẦN II: TỰ LUẬN (7,0 điểm).
Câu 7: (1,7 điểm)A,
Cho biểu thức A=√x√x+3+2√x√x−3+3x+99−x, với x≥0;x≠9.
a) Rút gọn biểu thức A.
b) Tìm giá trị của x để A=13.
Câu 8: (1,5 điểm)
Cho phương trình x2−2mx+m2−m+1=0, với x là ẩn; m là tham số.
a) Giải phương trình với m=2.
b) Tìm m để phương trình có hai nghiệm x1,x2 thỏa mãn x12+x22=x1x2+1
Câu 9: (2,5 điểm)
Cho tam giác ABC vuông tại đường cao AH(H∈BC). Đường tròn đường kính AH cắt hai cạnh AB,AC theo thứ tự là M và N.
a) Chứng minh tứ giác AMHN là hình chữ nhật.
b) Chứng minh tứ giác BMNC là tứ giác nội tiếp.
c) Qua A kẻ đường thẳng vuông góc với MN cắt BC tại I. Chứng minh rằng 1AI2=4AB2+AC2.
Câu 10: (1,5 điểm)
a) Sở Giáo dục và Đào tạo Bắc Ninh dự định tổ chức hội nghị tại hội trường 500 chỗ ngồi của trường THPT chuyên Bắc Ninh, hội trường được chia thành từng dãy ghế, mỗi dãy ghế có số chỗ ngồi như nhau. Vì có 567 người dự hội nghị nên ban tổ chức phải kê thêm 1 dãy ghế, đồng thời phải kê thêm 2 chỗ ngồi cho tất cả các dãy ghế thì vừa đủ số chỗ ngồi. Hỏi lúc đầu hội trường có bao nhiêu dãy ghế và mỗi dãy ghế có bao nhiêu chỗ ngồi?
b) Cho x,y là các số thực dương thỏa mãn x+y=2. Tìm giá trị lớn nhất của A=xy(x3+y3).
Đáp án và Hướng dẫn giải
Bài 1:
PHẦN I: TRẮC NGHIỆM
|
1 |
2 |
3 |
4 |
5 |
6 |
|
D |
C |
C |
D |
C |
A |
Câu 1
Phương pháp:
Biểu thức xác định
Biểu thức xác định
Cách giải:
Ta có: xác định
Chọn D.
Câu 2
Phương pháp:
Sử dụng công thức:
Cách giải:
Ta có:
Chọn C.
Câu 3
Phương pháp:
Sử dụng công thức lượng giác trong tam giác vuông:
Cách giải:
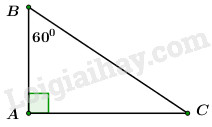
Xét tam giác vuông tại ta có:
Chọn C.
Câu 4
Phương pháp:
Tâm đường tròn ngoại tiếp hình vuông là giao điểm của hai đường chéo.
Bán kính đường tròn ngoại tiếp hình vuông cạnh là:
Cách giải:
Bán kính đường tròn ngoại tiếp hình vuông cạnh bằng là:
Chọn D.
Câu 5
Phương pháp:
Tính số đo
Sử dụng tính chất: Trong một đường tròn, góc nội tiếp có số đo = một nửa số đo góc ở tâm cùng chắn một cung.
Cách giải:
Ta có: là tiếp tuyến của tại
Xét vuông tại ta có:
Xét đường tròn ta có:
là góc nội tiếp chắn cung
là góc ở tâm chắn cung
Chọn C.
Câu 6 (VD)
Phương pháp:
Hàm số nghịch biến
Cách giải:
Hàm số nghịch biến
Lại có
Vậy có 5 giá trị nguyên của thỏa mãn bài toán.
Chọn A.
Câu 7:
Phương pháp giải:
a) Quy đồng mẫu số, biến đổi và rút gọn biểu thức.
b) Giải phương trình để tìm sau đó kết hợp với điều kiện rồi kết luận.
Lời giải chi tiết:
Cho biểu thức với
a) Rút gọn biểu thức
Điều kiện:
Vậy với
b) Tìm giá trị của để
Điều kiện:
Ta có:
(thỏa mãn)
Vậy để thì
Câu 8:
Phương pháp giải:
a) Thay vào phương trình rồi giải phương trình bậc hai tìm nghiệm.
b) Sử dụng định lý Vi-et để biến đổi biểu thức theo , từ đó tìm giá trị thỏa mãn.
Lời giải chi tiết:
Cho phương trình với là ẩn; là tham số.
a) Giải phương trình với
Thay vào phương trình ta được:
Vì nên phương trình có hai nghiệm là và
Vậy với thì phương trình có tập nghiệm là
b) Tìm để phương trình có hai nghiệm thỏa mãn
Ta có:
Phương trình có hai nghiệm
Với thì có hai nghiệm
Áp dụng hệ thức Vi-et ta có:
Theo đề bài ta có:
Vậy giá trị cần tìm.
Câu 9:
Phương pháp giải:
a) Chứng minh tứ giác có bốn góc vuông.
b) Chứng minh tứ giác có hai góc cùng chắn một cung bằng nhau.
Lời giải chi tiết:
Cho tam giác vuông tại đường cao Đường tròn đường kính cắt hai cạnh theo thứ tự là và
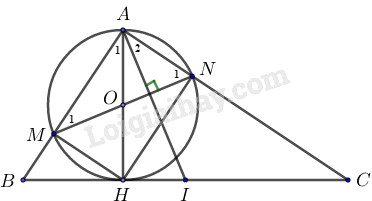
a) Chứng minh tứ giác là hình chữ nhật.
Gọi là tâm đường tròn đường kính
(góc nội tiếp chắn nửa đường tròn tâm )
(góc nội tiếp chắn nửa đường tròn tâm )
Do nên là hình chữ nhật (đpcm).
b) Chứng minh tứ giác là tứ giác nội tiếp.
Vì là hình chữ nhật nên
Suy ra tam giác cân tại nên
Mà (cùng phụ với góc )
Mặt khác (hai góc kề nhau)
Ta có: và hai góc này ở vị trí đối nhau
Suy ra tứ giác nội tiếp (dhnb) (đpcm).
c) Qua kẻ đường thẳng vuông góc với cắt tại Chứng minh rằng
Ta có:
Nên mà (theo b) cân tại
Chứng minh tương tự ta có cân tại nên
Vậy
Mà (đpcm).
Câu 10:
Phương pháp giải:
a) Gọi số dãy ghế lúc đầu là (dãy ghế)
Dựa vào các giả thiết đề bài cho biểu diễn các đại lượng chưa biết và các đại lượng đã biết theo ẩn vừa gọi và các đại lượng đã biết.
Từ đó lập phương trình, giải phương trình tìm ẩn
Đối chiếu với điều kiện đã đặt rồi kết luận.
b) Sử dụng giả thiết để biến đổi biểu thức để từ đó đánh giá và tìm GTLN của
Lời giải chi tiết:
a) Sở Giáo dục và Đào tạo Bắc Ninh dự định tổ chức hội nghị tại hội trường chỗ ngồi của trường THPT chuyên Bắc Ninh, hội trường được chia thành từng dãy ghế, mỗi dãy ghế có số chỗ ngồi như nhau. Vì có người dự hội nghị nên ban tổ chức phải kê thêm dãy ghế, đồng thời phải kê thêm chỗ ngồi cho tất cả các dãy ghế thì vừa đủ số chỗ ngồi. Hỏi lúc đầu hội trường có bao nhiêu dãy ghế và mỗi dãy ghế có bao nhiêu chỗ ngồi?
Gọi số dãy ghế lúc đầu là (dãy ghế)
Số chỗ ngồi trên mỗi dãy ghế lúc đầu là (chỗ).
Số dãy ghế lúc sau là (dãy).
Số chỗ ngồi trên mỗi dãy ghế lúc sau là: (chỗ).
Vì số chỗ ngồi trên mỗi dãy ghế lúc sau nhiều hơn số chỗ ngồi trên mỗi dãy ghế lúc đầu là chỗ nên ta có phương trình:
Vậy lúc đầu hội trường có dãy ghế, mỗi dãy ghế có chỗ ngồi.
b) Cho là các số thực dương thỏa mãn Tìm giá trị lớn nhất của
Ta có:
Mà
Dấu “=” xảy ra khi và chỉ khi
Vậy giá trị lớn nhất của là .
Đề thi Toán 9 Học kì 2 năm 2024 có đáp án (20 đề) - Đề 11
Phòng Giáo dục và Đào tạo .....
Đề thi Học kì 2
Môn: Toán lớp 9
Thời gian làm bài: 90 phút
(Đề 11)
I. TRẮC NGHIỆM (1 điểm) Chọn chữ cái đúng trước câu trả lời đúng.
Câu 1: Cặp số là nghiệm của hệ phương trình nào sau đây?
A. B.
C. D.
Câu 2: Điều kiện của m để phương trình có hai nghiệm là:
A. B.
C. D.
Câu 3: Cho đường tròn đường kính AB, dây. Khi đó số đo độ của cung nhỏ BC là:
A. B.
C. D.
Câu 4: Độ dài của một đường tròn là (cm). Diện tích của hình tròn đó là:
A. B.
C. D.
II. TỰ LUẬN (9 điểm)
Câu 1 (2,5 điểm):
1) Giải hệ phương trình sau:
2) Trong mặt phẳng tọa độ Oxy cho Parabol và đường thẳng
a) Với, hãy tìm tọa độ giao điểm của và .
b) Tìm m để và cắt nhau tại 2 điểm phân biệt và sao cho tổng các tung độ của hai giao điểm bằng 2.
Câu 2 (2,5 điểm): Giải bài toán bằng cách lập phương trình hoặc hệ phương trình.
Một đội xe theo kế hoạch chở hết 120 tấn hàng trong một số ngày quy định. Do mỗi ngày đội đó chở vượt mức 5 tấn nên đội đã hoàn thành kế hoạch sớm hơn thời gian quy định 1 ngày và chở thêm được 5 tấn. Hỏi theo kế hoạch đội xe chở hết số hàng đó trong bao nhiêu ngày?
Câu 3 (3,5 điểm): Cho đường tròn có dây cung CD cố định. Gọi M là điểm nằm chính giữa cung nhỏ CD. Đường kính MN của đường tròn cắt dây CD tại I. Lấy điểm E bất kỳ trên cung lớn CD (E khác C,D,N); ME cắt CD tại K. Các đường thẳng NE và CD cắt nhau tại P.
a) Chứng minh rằng: Tứ giác IKEN nội tiếp.
b) Chứng minh: .
c) NK cắt MP tại Q. Chứng minh: IK là phân giác của .
d) Từ C vẽ đường thẳng vuông góc với EN cắt đường thẳng DE tại H. Chứng minh khi E di động trên cung lớn CD (E khác C, D, N) thì H luôn chạy trên một đường cố định.
Câu 4 (0,5 điểm): Cho , chứng minh rằng:
Đáp án và Hướng dẫn giải
I. Trắc nghiệm
|
1A |
2B |
3B |
4D |
Câu 1:
Phương pháp:
Thay vào từng hệ phương trình để kiểm tra, nếu thỏa mãn thì là nghiệm và ngược lại.
Cách giải:
Vậy là nghiệm của hệ
Chọn A
Câu 2:
Phương pháp:
Từ dữ kiện đề bài sử dụng công thức nghiệm thu gọn kết hợp định lý Vi-ét để tìm m
Cách giải:
với mọi phương trình có hai nghiệm phân biệt với mọi
Ta có và theo định lý Vi-ét ta có:
Vậy với thỏa mãn yêu cầu đề bài.
Chọn B
Câu 3:
Phương pháp:
Sử dụng tính chất, dấu hiệu nhận biết tam giác đều để tính từ đó suy ra số đo cung nhỏ BC
Cách giải:
Cho đường tròn đường kính AB
Mặt khác dây
đều
(hai góc kề bù)
sđ (số đo góc ở tâm bằng số đo cung bị chắn)
Chọn B
Câu 4:
Phương pháp:
Từ công thức tính chu vi hình tròn rút ra R, từ đó tính diện tích hình tròn đó.
Cách giải:
Độ dài của một đường tròn chính là chu vi hình tròn
Diện tích hình tròn đó là:
Chọn D
II. Tự luận
Bài 1:
Phương pháp giải:
1) Đặt điều kiện cho hệ phương trình sau đó giải hệ phương trình bằng cách đặt ẩn phụ.
2) a) Thay vào phương trình đường thẳng d.
+) Lập phương trình hoành độ giao điểm, giải phương trình đó để tìm hoành độ 2 giao điểm, từ đó suy ra tọa độ của chúng.
b) cắt tại hai điểm phân biệt A và B phương trình hoành độ giao điểm có 2 nghiệm phân biệt
Từ đề bài tìm ra hệ thức liên hệ giữa và , biến đổi biểu thức đó sao cho chỉ còn và , sử dụng hệ thức Vi-ét thế vào để tìm m.
Lời giải chi tiết:
1) Giải hệ phương trình sau:
Điều kiện:
Đặt: khi đó hệ phương trình trở thành:
Vậy hệ phương trình có nghiệm duy nhất .
2) Trong mặt phẳng tọa độ Oxy cho Parabol và đường thẳng
a) Với , hãy tìm tọa độ giao điểm của và .
Phương trình hoành độ giao điểm của và là :
Với trở thành
Có
Với phương trình có hai nghiệm
Vậy với giao điểm của và là hai điểm có tọa độ và
b) Tìm m để và cắt nhau tại 2 điểm phân biệt và sao cho tổng các tung độ của hai giao điểm bằng 2.
Để cắt tại hai điểm phân biệt A và B (1) có hai nghiệm phân biệt
Gọi lần lượt là hoành độ của hai điểm A và B
là 2 nghiệm của (1)
Theo hệ thức Vi-ét ta có:
Vì và đều thuộc
Tổng các tung độ của hai giao điểm bằng 2
Vậy với thỏa mãn yêu cầu đề bài.
Bài 2:
Phương pháp giải:
+ Phân tích kỹ đề bài.
+ Gọi thời gian chở hàng theo kế hoạch là x (ngày), đã biết tổng số hàng theo kế hoạch và thực tế lập phương trình theo năng suất để tìm x.
Lời giải chi tiết:
Gọi thời gian đội đó chở hàng theo kế hoạch là x (ngày)
Năng suất của đội đó theo kế hoạch là (tấn/ngày)
Thời gian chở đội đó hàng thực tế là (ngày)
Năng suất thực tế đội đó chở hàng là (tấn/ngày)
Vì đội xe chở hàng vượt mức 5 tấn/ngày nên ta có phương trình
Vậy thời gian chở hàng theo kế hoạch là 6 ngày.
Bài 3:
Phương pháp giải:
+) Chứng minh IKEN là tứ giác có tổng hai góc đối bằng
+) Chứng minh (g.g) để suy ra đpcm
+) Chứng minh tứ giác NIQP nội tiếp kết hợp a) để suy ra từ đó ta được đpcm
Lời giải chi tiết:
a) Chứng minh rằng: Tứ giác IKEN nội tiếp.
Xét đường tròn đường kính MN có M là điểm chính giữa cung nhỏ CD
tại I
(góc nội tiếp chắn nửa đường tròn)
Xét tứ giác IKEN có:
Mà 2 góc này ở vị trí đối nhau nên tứ giác IKEN nội tiếp. (dhnb)
b) Chứng minh: .
Tứ giác IKEN nội tiếp (cmt) nên (góc nội tiếp cùng chắn cung IK )
Xét và có:
(đpcm)
c) NK cắt MP tại Q. Chứng minh: IK là phân giác của .
Xét có:
là trực tâm tại
Xét tứ giác NIQP có mà 2 góc này cùng nhìn đoạn NP
Tứ giác NIQP nội tiếp (dhnb) (hai góc nội tiếp cùng chắn cung PQ) (1)
Tứ giác IKEN nội tiếp (cm a) (cùng chắn EK) (2)
Từ (1) và (2) IK là phân giác của
d) Từ C vẽ đường thẳng vuông góc với EN cắt đường thẳng DE tại H. Chứng minh khi E di động trên cung lớn CD (E khác C, D, N) thì H luôn chạy trên một đường cố định.
Ta có: (từ vuông góc đến song song)
(đồng vị) ;
(so le trong)
Mà (2 góc nội tiếp chắn 2 cung bằng nhau)
cân tại E Þ EN là trung trực của CH (tính chất)
Mặt khác dễ dàng chứng minh IN là trung trực của CD
N là tâm đường tròn ngoại tiếp
Mà N, C, D cố định H thuộc đường tròn tâm N cố định bán kính NC không đổi (đpcm)
Bài 4:
Phương pháp giải:
Chứng minh và , từ đó suy ra đpcm.
Lời giải chi tiết:
Cho , chứng minh rằng:
Áp dụng bất đẳng thức Cô-si cho hai số dương a và ta được:
Chứng minh tương tự ta được:
Cộng (1), (2) và (3) vế theo vế ta được: (*)
Ta chứng minh
Thật vậy ta có
(luôn đúng do )
Tương tự ta có
Cộng (4), (5) và (6) vế theo vế ta được: (**)
Từ (*) và (**) suy ra (đpcm)
Đề thi Toán 9 Học kì 2 năm 2024 có đáp án (20 đề) - Đề 12
Phòng Giáo dục và Đào tạo .....
Đề thi Học kì 2
Môn: Toán lớp 9
Thời gian làm bài: 90 phút
(Đề 12)
Câu 1: Giải các phương trình sau:
a)
b)
Câu 2: Một mảnh đất hình chữ nhật có chu vi 80m, biết ba lần chiều rộng kém 2 lần chiều dài là 5m. Tính diện tích mảnh đất.
Câu 3: Cho hàm số:
a) Vẽ đồ thị d và P.
b) Tính tọa độ giao điểm d và P.
Câu 4: Cho phương trình:
a) Chứng tỏ phương trình trên luôn có 2 nghiệm phân biệt với mọi m.
b) Tìm m để phương trình có 2 nghiệm phân biệt thỏa mãn:
Câu 5: Một trường tổ chức cho 250 người bao gồm giáo viên và học sinh đi tham quan Suối Tiên. Biết giá vé vào cổng giáo viên là 80.000 đồng, học sinh là 60.000 đồng, đi vào đúng dịp giỗ tổ Hùng Vương nên giảm 5% vé vào, vì vậy nhà trường phải trả tổng cộng 14.535.000 đồng. Hỏi có bao nhiêu giáo viên và học sinh đi tham quan?
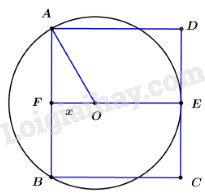
Câu 6: Đường tròn đi qua 2 đỉnh và tiếp xúc cạnh 1 hình vuông. Tính bán kính R của đường tròn biết cạnh hình vuông là 12 cm.
Câu 7: Từ A ngoài (O), vẽ tiếp tuyến AB, AC, H là giao OA và BC.
a) Chứng minh tứ giác OBAC nội tiếp và OA vuông BC.
b) Qua C vẽ d // OA, qua O vẽ đường vuông góc OB cắt (O) và d tại F và K (O nằm giữa F và K), AF cắt (O) tại E. Chứng minh rằng:
c) Chứng minh OCKA là hình thang cân.
Đáp án và Hướng dẫn giải
Bài 1:
Phương pháp giải:
Đây là các phương trình bậc 2 và trùng phương, ta đưa về phương trình tích.
Lời giải chi tiết:
Vậy tập nghiệm của phương trình là:
Đặt , phương trình (*) trở thành:
Vậy tập nghiệm của phương trình là:
Bài 2:
Phương pháp giải:
Giải bài toán bằng cách lập phương trình:
+) Gọi ẩn và đặt điều kiện cho ẩn.
+) Biểu diễn các đại lượng chưa biết theo ẩn vừa gọi và các đại lượng đã biết.
+) Dựa vào dữ kiện bài toán để lập phương trình.
+) Giải phương trình vừa lập sau đó đối chiếu với điều kiện đề bài và kết luận.
Lời giải chi tiết:
Gọi chiều rộng mảnh đất là
Nửa chu vi của mảnh đất là:
Chiều dài của mảnh đất là:
Do 3 lần chiều rộng kém 2 lần chiều dài là 5m nên ta có phương trình:
Chiều dài mảnh đất là :
Diện tích mảnh đất là : 15.25 =
Bài 3:
Phương pháp giải:
1) Lập bảng giá trị các điểm thuộc đồ thị hàm số (P) và vẽ đồ thị hàm số.
2) Lập phương trình hoành độ giao điểm của (d) cắt (P).
+) Để (d) cắt (P) tại hai điểm phân biệt thì phương trình hoành độ giao điểm phải có hai nghiệm phân biệt tức là
Lời giải chi tiết:
Cho hàm số:
a) Vẽ đồ thị d và P.
+) Vẽ đồ thị hàm số :
Ta có bảng giá trị:
|
|
|
|
0 |
2 |
4 |
|
|
|
|
0 |
|
|
Vậy đồ thị hàm số là đường cong đi qua các điểm +) Vẽ đồ thị hàm số
Ta có bảng giá trị:
|
|
0 |
|
|
|
|
0 |
Vậy đồ thị hàm số là đường thẳng đi qua các điểm
b) Tính tọa độ giao điểm (D) và (P).
Phương trình hoành độ giao điểm của hai đồ thị hàm số là:
Vậy tọa độ giao điểm là:
Bài 4:
Phương pháp giải:
Bước 1: Tìm m để phương trình (1) có hai nghiệm phân biệt : Phương trình (1) có hai nghiệm phân biệt
Bước 2: Phân tích biểu thức A về dạng chứa các hệ thức Viet sau đó áp dụng hệ thức Vi-et vào tìm được m và đối chiếu với điều kiện sau đó kết luận.
Hệ thức Viet như sau:
Lời giải chi tiết:
Cho phương trình:
a) Chứng tỏ phương trình trên luôn có 2 nghiệm phân biệt với mọi m.
Ta có với mọi m
Do đó phương trình trên luôn có 2 nghiệm phân biệt với mọi
b) Tìm m để phương trình có 2 nghiệm phân biệt thỏa mãn:
Áp dụng định lý Viet ta có:
Theo đề bài ta có :
Vậy thỏa mãn yêu cầu bài toán.
Bài 5:
Phương pháp giải:
Giải bài toán bằng cách lập hệ phương trình:
+) Gọi ẩn và đặt điều kiện cho ẩn.
+) Biểu diễn các đại lượng chưa biết theo ẩn vừa gọi và các đại lượng đã biết.
+) Dựa vào dữ kiện bài toán để lập hệ phương trình.
+) Giải hệ phương trình vừa lập sau đó đối chiếu với điều kiện đề bài và kết luận.
Lời giải chi tiết:
Gọi số giáo viên là số học sinh là (người),
Tổng số giáo viên và học sinh đi tham quan là 250 người nên ta có phương trình:
Giá tiền vé vào cổng của mỗi giáo viên sau khi giảm giá là: (đồng)
Giá tiền vé vào cổng của mỗi học sinh sau khi giảm giá là: (đồng)
Tổng số tiền nhà trường phải trả là 14.535.000 đồng nên ta có phương trình:
Từ (1) và (2) ta có hệ phương trình:
Vậy: có 15 giáo viên và 235 học sinh đi tham quan.
Bài 6:
Phương pháp giải:
Áp dụng định lý Pytago, lưu ý điểm tiếp xúc E sẽ là trung điểm CD.
Lời giải chi tiết:
Giả sử hình tròn đi qua hai đỉnh A, B và tiếp xúc với cạnh CD của hình vuông ABCD.
Ta có hình vẽ:
Gọi là điểm tiếp xúc của và
Kéo dài cắt tại là trung điểm của
Gọi
Ta có:
Áp dụng định lý Pi-ta-go cho vuông tại ta có:
Lại có:
Thay vào (*) ta được:
Vậy bán kính đường tròn thỏa mãn yêu cầu bài toán là:
Bài 7:
Phương pháp giải:
a) Chứng minh đây là tứ giác có 2 góc đối diện vuông.
b) Sử dụng 2 cặp tam giác đồng dạng và AB = AC để suy ra hệ thức.
c) Sử dụng tính chất hình thang nội tiếp đường tròn là hình thang cân.
Lời giải chi tiết:
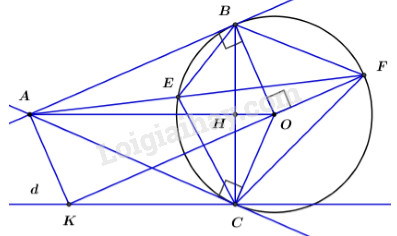
a) Chứng minh tứ giác OBAC nội tiếp và OA vuông BC.
Do AB, AC là tiếp tuyến từ A đến (O) nên:
Xét tứ giác ta có:
là tứ giác nội tiếp (dhnb).
Ta có: (tính chất hai tiếp tuyến cắt nhau)
cân tại (định nghĩa)
Lại có: là phân giác của (tính chất hai tiếp tuyến cắt nhau)
vừa là đường cao, vừa là đường phân giác của (đpcm)
b) Qua C vẽ d // OA, qua O vẽ đường vuông góc OB cắt (O) và d tại F và K (O nằm giữa F và K), AF cắt (O) tại E. Chứng minh rằng:
Ta có: (sđ cung (góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cung chắn cung ).
(đpcm)
Vì (các cặp cạnh tương ứng tỉ lệ)
Ta có: sđ cung (góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cung cùng chắn cung EC)
(đpcm)
c) Chứng minh OCKA là hình thang cân.
Ta có: là hình thang (định nghĩa).
Lại có:
Vì (từ vuông góc đến song song)
Mặt khác (tính chất hai tiếp tuyến cắt nhau)
là tứ giác nội tiếp (dhnb).
Hình thang nội tiếp tứ giác là hình thang cân là hình thang cân (đpcm)
TuandungIT
2021-12-14 15:26:45
hay quá